水下声散射问题的奇异积分研究

（海军工程大学理学院 武汉 430033）

0 引 言

水下目标声散射特性研究是水声技术中的重要课题，主要研究方法有高频近似方法和低频数值方法．随着计算机的高速发展，低频数值方法在声散射特性研究中得到快速发展．边界元法作为一种水下声散射问题研究中常用方法，具有降低问题空间维数、自动满足Helmholtz方程等优点，但是存在两个数值计算上的难点，一个是奇异积分、近奇异积分的计算，主要的解决方法有坐标变换方法、Roberto D G提出的利用梯度定理消除积分奇异性方法、基于Cauchy主值积分的Gauss积分法等，另一个是Helmholtz外问题在特征频率处解的非唯一性问题，主要有CHIEF方法和B－M方法等．

当场点位于源域内时，就会产生奇异积分的元素；当场点和源域十分接近但不在源域内时的积分，则会产生近奇异积分的元素，从理论上说，此时积分是非奇异的，但从计算结果可以发现，当场点接近源域时，被积函数在积分区间内变化非常迅速，而且场点和源域距离越近，积分值变化越剧烈．当场点充分远离源域时，可以通过Gauss积分公式计算得到准确结果，然而随着场点逐渐接近源域，通过Gauss积分公式计算得到的结果精度会急剧降低，这就是所谓的“边界层效应”．

对于边界元法中奇异积分和近奇异积分，采用全局法（global approach）加以解决，推导得到了积分的数值计算表达式，通过该表达式计算边界元法中的积分，对刚性球的水下散射特性进行了仿真研究，仿真结果证明了本文方法的有效性和正确性，且较坐标变换方法等常用于奇异积分计算的方法具有计算效率高、计算精度高等优点．

1 声散射特性研究的建模方法

Kirchhoff表面积分方程在平面波入射下，任意形状、任意表面阻抗目标表面的散射声场经离散化处理后为［1－2］

通过3ds max将目标表面离散为N个三角形面元，通过（1）式得到一个N×N的关于ps矩阵方程组，计算该方程组即可得到ps值，将ps代入Kirchhoff外部积分方程即可计算得到空间中任意一点的散射声场值．矩阵系数的数值计算难点是两类静态项积分的计算，即

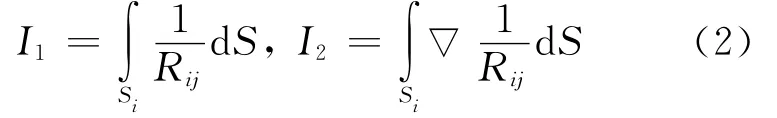
2 积分方程中两类积分的计算

对于度为α的齐次函数积分I在积分区域S内的积分

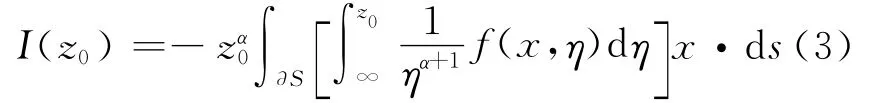
式中：z0为常数．式（3）即为全局积分方法将面积分转变为曲线积分的公式．为便于处理，将S做平移变换（－u0，－v0），变换后O为三角形的重心就满足了齐次性的要求，可以通过全局法计算．

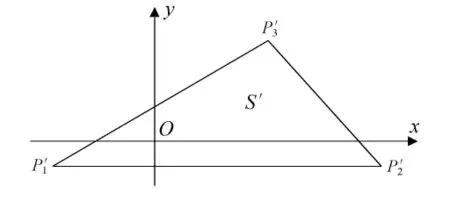
图1 第i个三角形坐标变换后的积分区域S′

根据式（3）有

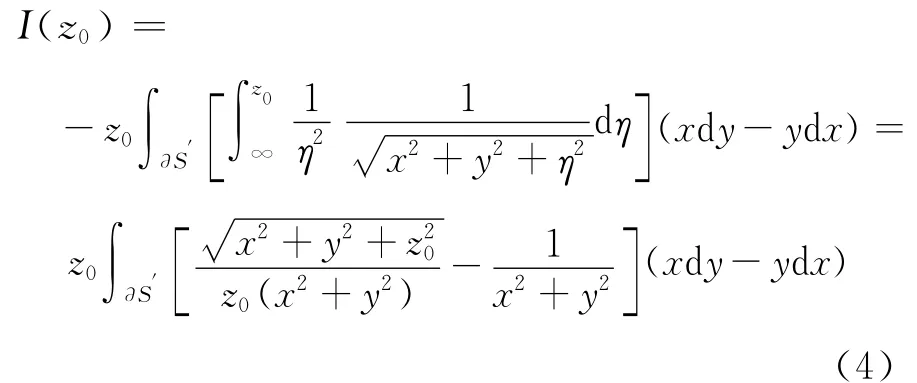
使用全局法处理后，积分由最初的面积积分转化为计算沿三角形单元边界的线积分，线积分方向取逆时针．见图1．因此P3在局部坐标系（O；x，y，z）中的落点对积分计算影响较大，下面进行说明．为了方便处理，采用局部坐标系来进行说明，以三角形面元一条边做x轴，取与其垂直的为y轴．设三角形单元3个顶点为Pi（xi，yi，zi），i＝1，2，3，坐标变换后3个顶点坐标分别为P′1（－u0，－v0），P′2（l3－u0，－v0），P′3（u3－u0，v3－v0）．

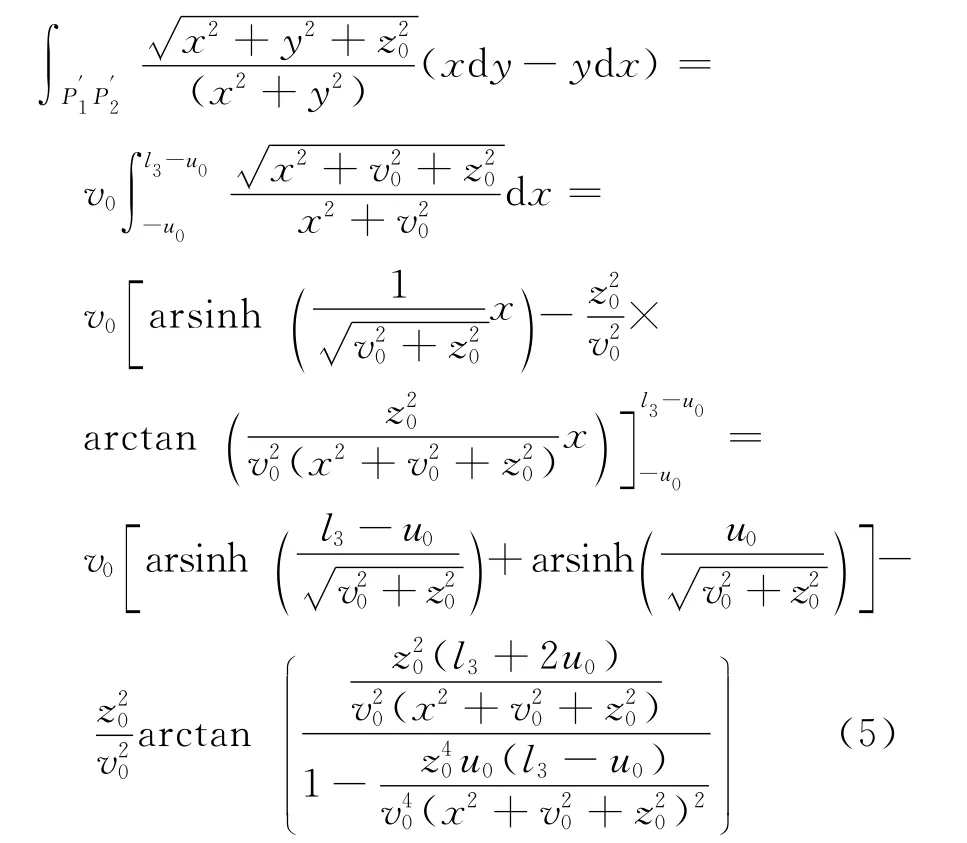
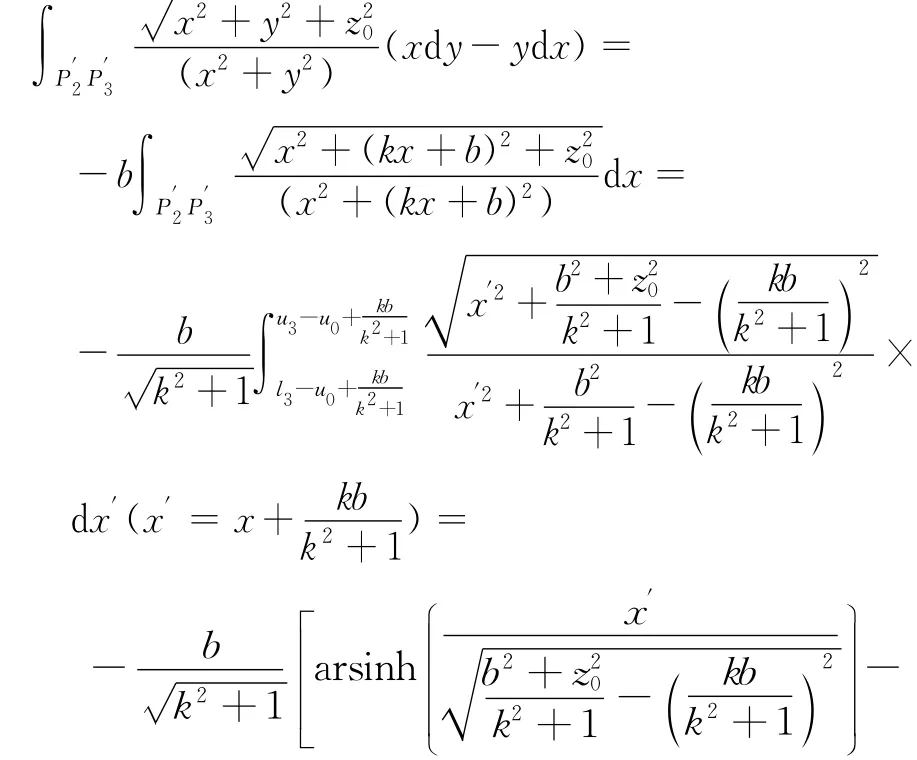
经过上述处理后，边界元法中面积分就转化为线积分，通过处理化成为闭合数值表达式，提高了边界元的计算效率；由于积分计算过程中并没有采用近似计算，计算精度很高．

根据式（8），式（9）即可计算得到奇异积分I1的数值．

第一部分可以通过2．2节的计算结果求解，下面对第二项的数值计算进行研究．

代入式（11）即可得到积分I2的数值．

2.4 数值算例

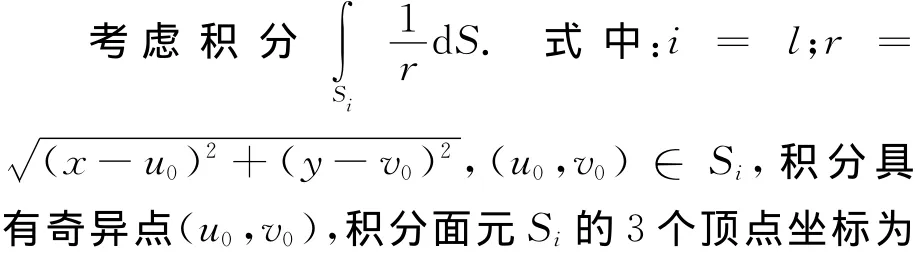
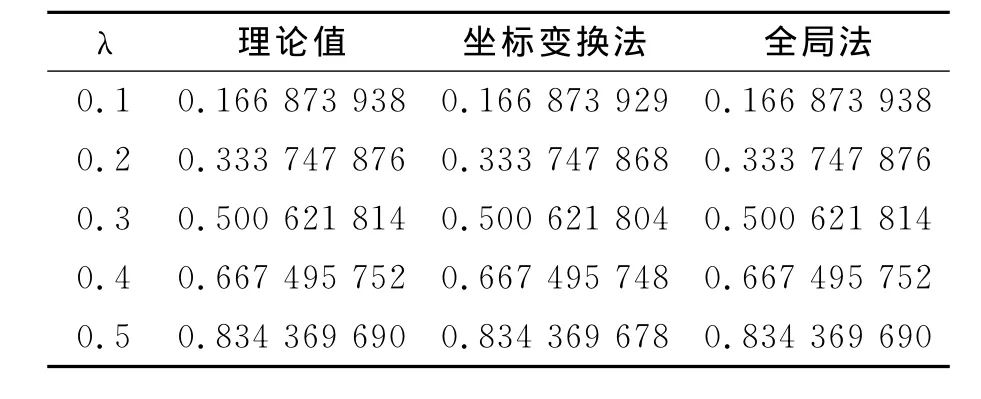
表1 I1与坐标变换方法比较

3 仿真算例与结果分析

用刚性球的目标强度来检验方法的正确性和可行性，在全波数范围内，对半径为1的刚性球的后向散射强度进行计算．目标中心位于坐标原点，入射波为平面波，方位角α＝π，极角β＝，介质密度为1 040kg／m3，声速为1 460m／s，接收点与坐标原点的距离为20m．将第2节的结论计算边界元法中积分，使用Matlab软件进行仿真，仿真结果见图2．

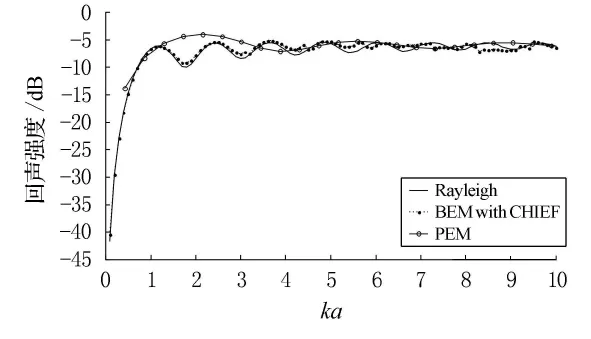
图2 刚性圆球后向散射强度

板块元法（planar element method，PEM）是目前最常用的高频近似计算方法，Rayleigh简正级数解，是刚性球回声强度的理论解析值．由于边界元法在特征频率处存在解的非惟一性，通过引入CHIEF方法有效克服了这一缺点．数值计算结果在低、中频处与解析值一致性很好，计算精度很高，计算精度、计算速度都明显优于板块元法；当ka逐渐增大时，误差逐渐增大，这主要是高频处需要的离散单元数更多才能满足和低、中频相同的精度要求．因此边界元法用于低、中频处的散射特性研究是一种很有前途的方法．

4 结束语

全局法提供了一种全新的奇异积分数值计算方法，通过与坐标变换方法的奇异积分计算结果比较证明了本方法的正确性，且计算精度很高；通过全局法将面积分转化为沿边界计算的线积分，从而得到了闭合计算表达式，提高了积分的计算效率．仿真结果表明，将本文的积分计算公式用于水下散射声场计算中，解决了系数矩阵中存在的奇异积分、近奇异积分，提高了边界元法的计算效率，且在低、中频处得到的数值精度非常高．

［1］徐忠昌，吴冬冬．声场计算中一类奇异积分的数学处理［J］．舰船电子工程，2009，181（7）：173－175．

［2］梁昌洪，李 龙，史小卫．Green函数自作用积分奇异项的简洁闭式［J］．电波科学学报，2003，18（2）：121－126．

［3］SINATHURAI V，DONALD E C．An invariant imbedding method for singular integral evaluation on finite domains［J］．SIAM，1988，48（6）：1335－1349．

［4］DAN R，DONALD E C．The continuation approach：A general framework for the analysis and evaluation and near－singular integrals［J］．SIAM，1995，55（2）：723－762．

［5］DAN R，DONALD E C．Singular and near－singular integrals in the BEM：A global approach［J］．SIAM，1993，53（2）：340－357．

［6］程广利，刘成元，张明敏．混合法研究水下刚性目标全波数散射特性［J］．武汉理工大学学报：交通科学与工程版，2009，33（4）：745－748．

［7］刘成元．水下目标声散射建模研究［D］．武汉：海军工程大学，2007．

［8］王 斌，汤渭霖，范 军．一种辐射声场近似计算方法－单元辐射叠加法［J］．声学学报，2008，33（3）：226－230．

［9］KEUHNWA L，WOOJAE S．Time－domain Kirchhoff model for acoustic scattering from an impedance polygon facet［J］．Acoustical Society of America，2009，126（1）：14－21．

［10］李建鲁，范 军，汤渭霖．水下简单形状目标回声的近远场过渡特性［J］．上海交通大学学报，2001，35（12）：1846－1850．