基于EMD方法的我国主要海港货物吞吐量变化规律研究*
李志强
(广东海洋大学工程学院 湛江 524088)
0 引 言
港口货物吞吐量是个十分复杂的变量,受诸多因素的影响.港口所处的地理位置与自然条件、腹地经济水平、政策环境、国际经济形势、港口通过能力、集疏运系统、港口运营情况、港口货物组成结构、工农业生产的季节性、车船到港的均衡性等对港口吞吐量都有显著的影响[1-2].科学准确的货物吞吐量预测对港口的总体布局、建设规模以及港口集疏运等配套设施建设有重要的指导意义.国内对港口吞吐量的预测研究比较多,例如线性与非线性回归法、指数平滑法、神经网络、灰色模型及组合模型预测等[3-4].不少研究指出这些方法在不同港口预测中的有效性是有差别的[5-6].受诸多线性和非线性因素影响,港口吞吐量的变化很复杂[7-10],直接将统计数据代入数学模型中进行预测是不科学的,必须从港口吞吐量数据本身入手,分析其中蕴含的规律,才可以为港口运营管理、新建扩建等工程提供可靠依据的预测.为此,本文将引进经验模态分解(empirical mode decomposition,EMD)方法,对我国沿海主要港口港口吞吐量的近10年来的主要变化规律进行探讨.
1 理论分析
港口吞吐量受非线性因素的影响,具有非平稳性.非平稳要素的变化过程包含周期性、突变性和趋势性的基本特征.对于非平稳过程,一般可以用一个线性叠加模型来描述
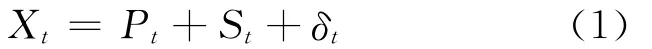
式中:Xt为要素变化时间序列;Pt为变化的趋势成分;St为变化的周期成分;δt为随机相依成分和纯随机成分[11].对于非平稳时间序列,趋势成分可以看作是周期比实测序列长得多的长周期低频成分,例如港口的长期成长过程.随机成分是由不规则的振荡和随机因素造成的,如车船到港的均衡性、港口气象条件等.周期成分是由确定性的因素引起,如工农业生产的季节性,人类特定消费活动的周期性等.
Huang等提出的经验模态分解是近年来广泛应用的处理非线性时间序列的新方法[12-13].它的优点是能够很好地对非线性、非平稳的数据进行线性化和平稳化处理,同时在分解后能保留数据本身的特性.如果在此基础上再进行Hilbert变换,得到各分量的瞬时频率和瞬时振幅,就可以揭示时间序列的多尺度变化规律.
2 EMD和Hilbert变换方法
2.1 经验模态分解法
EMD的基本假设是:如果一个原始的数据系列X(t)中极大值或极小值的数目比上跨零点或下跨零点的数目多2个或2个以上,则该数据序列就需要进行平稳化处理.最终把时间信号X(t)分解成一系列本征模态函数(intrinsic mode function)IMFi(t)和一个趋势分量R(t).IMF 分量应满足:(1)极值点数必须和过零点数必须一致或者至多相差一个;(2)在某一个局部点,极大值包络和极小值包络在该点的值的算术平均和趋近零或小于给定值.
EMD分解过程是:
1)找出序列X(t)所有极大值和极小值点,分别用三次样条函数拟合,得到上下包络线.
2)求得到平均包络线m1,将原序列减去m1可得到去掉低频的新序列h1.一般h1不是平稳的,不满足IMF的条件,需将h1作为原始数据多次重复上述过程,使平均包络线趋近于零,,得到第一个IMF分量IMF1(t).
3)从X(t)中分离出IMF1(t),得到剩余序列r1(t)=X(t)-IMF1(t),将r1(t)作为一个新的原序列,按照以上步骤.当残余量rn(t)成为一个单调函数或常量,不能再从中提取满足条件的IMF分量时,分解即结束.如果把分离出来的IMF分量与最终的残余量加起来,则可得到原始数据序列,即
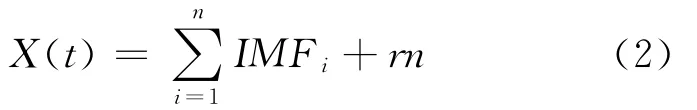
2.2 Hilbert变换
通过EMD,就可以对每个内在模态函数进行Hilbert变换,求出瞬时频率.对每一个IMF分量IMFi进行Hilbert变换
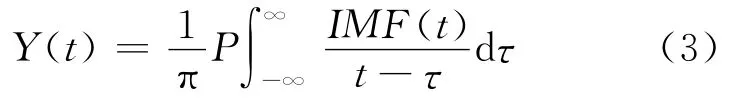
式中:P为积分的柯西主值.
定义IMF(t)的解析信号Z(t)
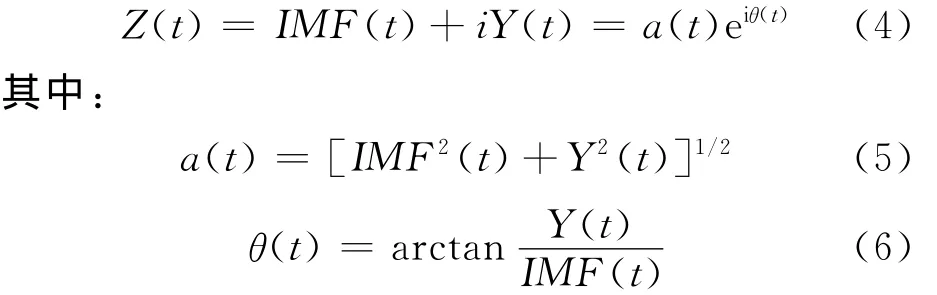
式中:a(t),θ(t)分别为Z(t)的瞬时振幅和瞬时相位.在此基础上定义瞬时频率ω(t)为
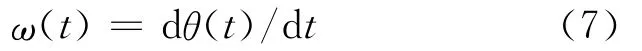
EMD方法和数字滤波器、小波变换等方法一样,都存在端点效应的处理,本文采用的端点处理方法是镜像对称延拓方法[14].
3 数据处理与结果分析
3.1 数据处理
根据交通运输部综合规划司公布的我国沿海规模以上港口货物吞吐量逐月公报,选择2001年1月至2010年12月的数据建立沿海15个主要港口的货物吞吐量时间序列[15].统计公报一般没有当年12月份的数据,这里采用全年总吞吐量减去前11个月吞吐量总和的办法得到.由于港口吞吐量统计和公报制度上的一些原因,存在个别月份数据异常现象,本文采用前后2个月平均的办法消除.黄骅、唐山、温州、北部湾等港口由于统计数据有限,这里不选用.舟山港和宁波港自2006年1月后统计数据合并,这里也不采用.
3.2 结果分析
3.2.1 吞吐量变化模态与周期 经过经验模态分解后,各个港口吞吐量由原来的非线性时间序列,分别分解成若干个模态,分别表示不同的时间尺度.限于篇幅,这里仅绘出深圳港吞吐量分解结果.由图1可见,经过EMD分解后,原始非平稳的时间序列,被分解成4个平稳的内在模态分量及一个趋势分量.各模态表现出由高频到低频的特征.其中第一个内在模态分量显示出随机相依的特征.后面的模态函数均表现出周期振荡特征,是吞吐量周期变化成分.
再经过Hilbert变换以后,就可以求得各模态的瞬时频率,进而求得各模态的平均频率和平均周期.各个港口各内在模态分量的平均周期见表1.由表1可见,我国沿海港口吞吐量具有3~5个变化周期,大致对应于季度、半年、年和多年变化周期,这些变化周期是由于港口货物吞吐量影响要素的变化周期引起的[16].
3.2.2 我国港口吞吐量的发展趋势 模态分解的趋势分量反映的是时间序列长期变化趋势.进入21世纪以来,我国经济发展加速,已经成为“世界工厂”.因此,除福州港外我国沿海主要港口吞吐量基本上都呈现出稳步上升的趋势,而且占吞吐量总量的比重最大,说明我国港口吞吐量的增长势头强劲.值得指出的是,基本上所有港口在2009年后增长势头有所放缓.其趋势分量与图1中深圳港的趋势分量形式基本一样.福州港货物吞吐量下降是因为该港最大宗的货物为河沙出口,占该港吞吐量的一半以上.统计数据表明,国家禁止河沙出口之后,福州港的吞吐量大幅下降,2007年3月份吞吐量仅为383万t,仅为2006年同期的47.45%,2007年1~3月累计吞吐量为1 677万t,为前1年同期的81%.
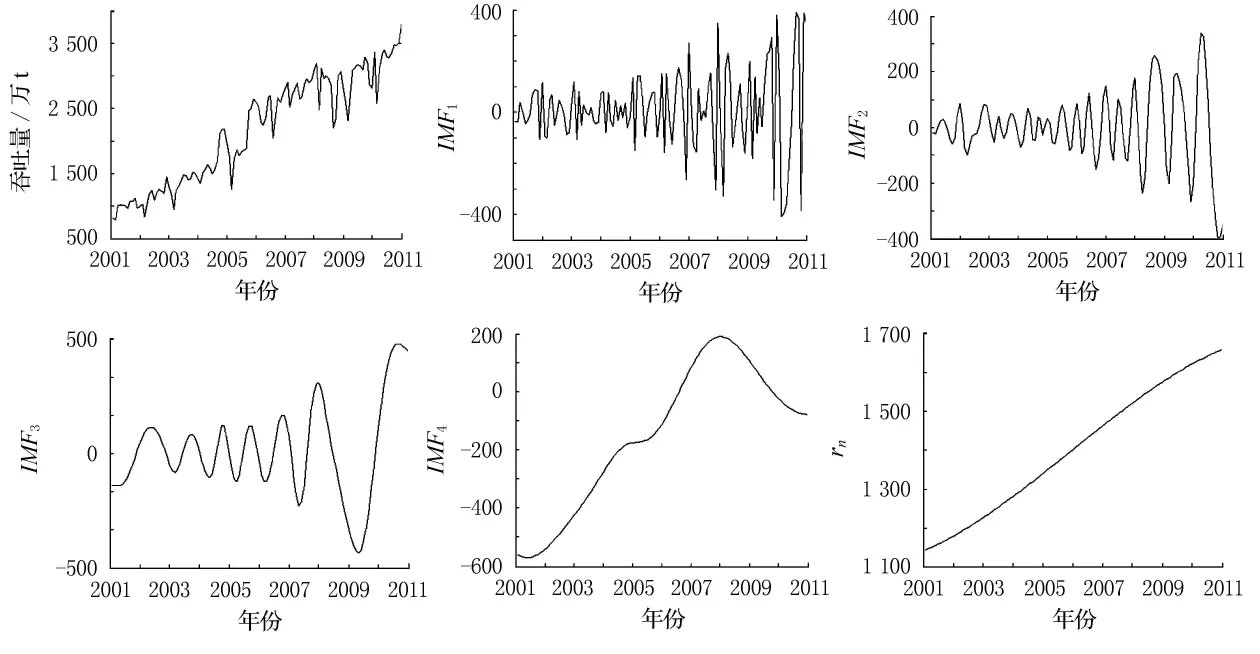
图1 深圳港吞吐量EMD分解结果
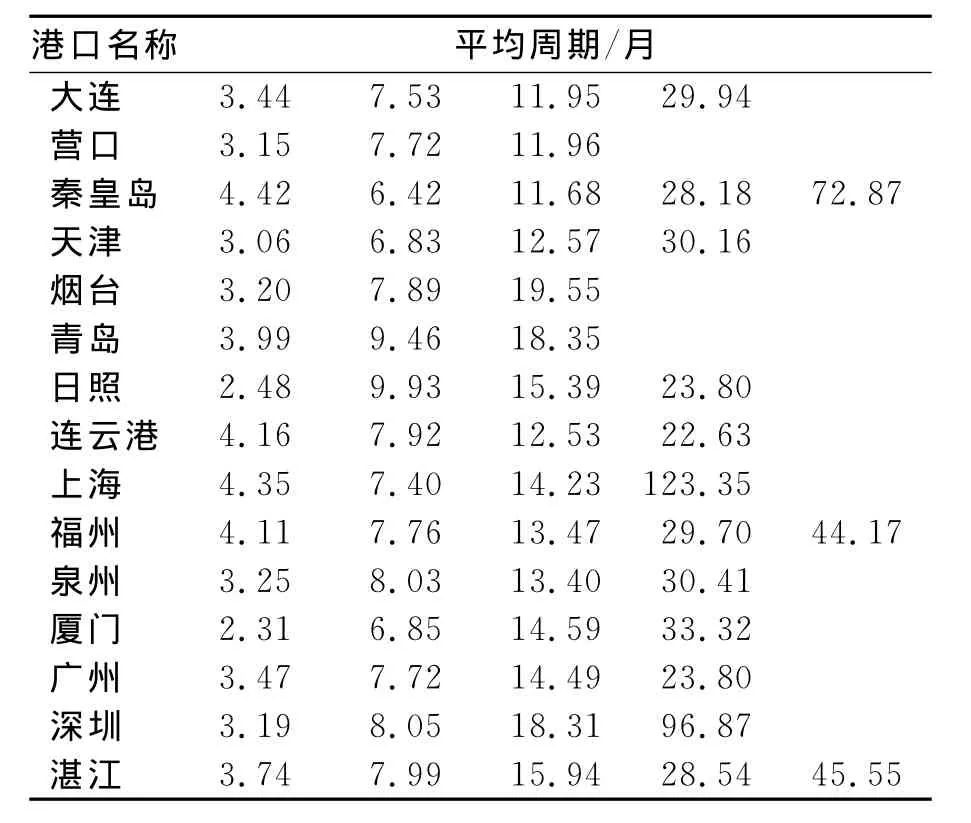
表1 各港口吞吐量变化各内在模态的平均周期
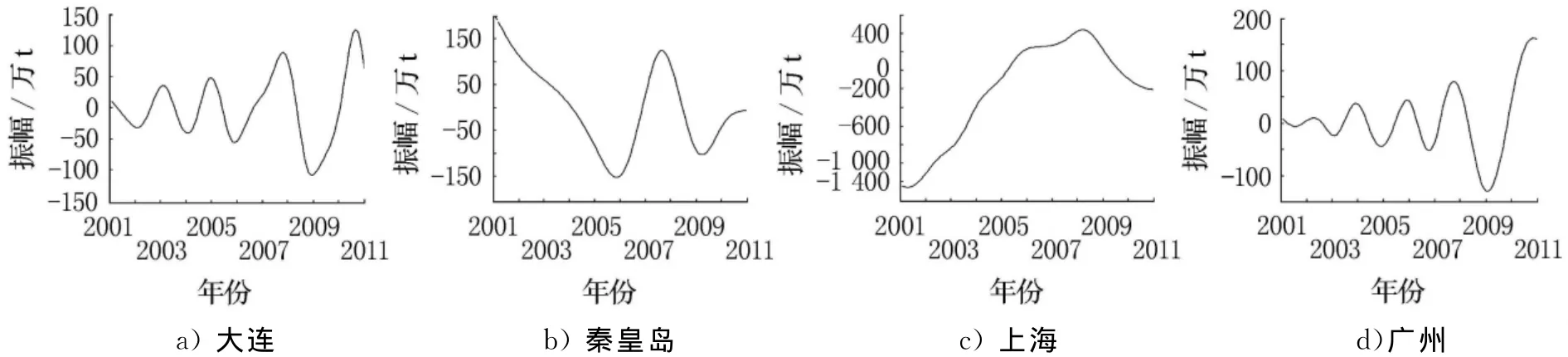
图2 金融危机对港口吞吐量的影响
3.2.3 金融危机对我国港口吞吐量的影响 受金融危机影响,2008年12月份我国对外进出口贸易总额同比下降11.1%,这是多年来我国对外进出口首次出现负增长.通过EMD分解,这一现象在港口吞吐量内在模态上有显著的反映.由于国际贸易具有较长周期的变化规律,因此金融风暴对港口吞吐量的影响主要体现在对港口吞吐量长周期变化分量上.图2列出了大连港、秦皇岛港、上海港和广州港的长周期内在模态分量.可以看到这些港口在2008年下半年后,吞吐量均振幅出现显著的下降,这一规律在其他港口业可以清楚观察到.这充分说明了金融危机对我国沿海港口吞吐量的重大影响.
3.2.4 内在模态对吞吐量预测的意义 对国内吞吐量预测研究进行总结可以看到,现在用来预测港口吞吐量的方法多基于经验和推断的拟合,属于“黑箱”或“灰箱”模型,一般没有考虑到吞吐量数据的内在变化规律.由图1可以看到,EMD分解得到的是一系列周期性的波动过程和一个趋势项.各个波动模态变化周期比较稳定且意义比较明确,振幅变化在一定范围之内.可以通过对各模态进行拟合,建立多尺度统计动力预报模型来预测吞吐量[17].因此,吞吐量变动内在模态的揭示为吞吐量的预报提供了一个新的思路.
4 结 论
1)我国沿海港口货物吞吐量具有3~5个变化周期,对应于季度、半年、年和多年变化周期.
2)21世纪以来,我国沿海主要港口货物吞吐量基本上都呈现出稳步上升的趋势,但在2009年后增长势头有所放缓.
3)金融危机对港口吞吐量的影响主要体现在对港口吞吐量长周期变化分量上.EMD方法有效的揭示了金融危机对吞吐量的影响.
[1]马清涛.2010年我国沿海港口发展情况简述[EB/OL].http://www.tranbbs.com/Techarticle/PTraffic/Techarticle_80264.shtml.
[2]王 丹,杨 赞.港口吞吐量影响因素分析[J].水运工程,2007(1):45-48.
[3]张 萍,严以新,许长新.港口吞吐量预测的系统动力学模型构建[J].武汉理工大学学报:交通科学与工程版,2006,30(6):950-953.
[4]祝 建.我国港口吞吐量预测方法研究综述[J].中国水运,2010(11):34-35.
[5]刘勇南.对东莞市港口吞吐量预测方法的思考[J].水运工程,2006(7):1-3.
[6]徐兴亚,杨 磊,李晓英.连云港港货物吞吐量预测研究[J].水运工程,2011(4):63-66.
[7]杨中庆,赵彬彬,廖慧敏.灰色组合模型在港口集装箱吞吐量预测中的应用[J].水运工程,2006(9):14-16.
[8]王再明,王宏波.灰色系统理论在港口吞吐量预测中的应用[J].武汉理工大学学报:交通科学与工程版,2005,29(3):456-459.
[9]陈 宁,朱美琪,余珍文.基于对数二次指数平滑的港口吞吐量预测[J].武汉理工大学学报:交通科学与工程版,2005,27(9):77-79.
[10]张 浩.基于最优线性组合的港口集装箱吞吐量预测方法[J].武汉理工大学学报:交通科学与工程版,2007,31(2):373-376.
[11]郑红星,刘昌明.黄河流域水资源演化模式分析[J].地理学报,2004,59(2):267-273.
[12]HUANG N E,SHEN Z.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[C]//Proceedings of the Royal Society London,1998,454:903-995.
[13]HUANG N E,SHEN Z,LONG S R.A new view of nonlinear water waves:the Hilbert spectrum[J].Ann Rev Fluid Mech,1999,31:417-457.
[14]ZHAO Jinping,HUANG Daji.Mirror extending and circular spline function for Empirical Mode Decomposition method[J].Journal of Zhejiang University:Science,2001(2):247-252.
[15]中华人民共和国交通运输部综合规划司.规模以上港口货物、旅客吞吐量[EB/OL].http://www.moc.gov.cn/zhuzhan/tongjigongbao/tongjishuju/gonglushui-yunyewu/gangkouhuowu_LKTTL/.
[16]李志强,胡伟剑.港口吞吐量变动的内在特征研究[J].水运工程,2012(2):63-66.
[17]LOEHLE C.Detection and attribution of trends from long-term geologic data[J].Ecological Modelling,2002,171:433-450.

