基于动态PCA 的核动力装置传感器故障检测

宋梅村 蔡 琦

（海军工程大学船舶与动力学院 武汉 430033）

为了核动力装置安全可靠运行，由现场传感器获取的数据必须是准确、合理的，为此，需要对来自现场传感器的数据进行验证.其中传感器的故障检测是整个验证工作的基础.传感器通常有如下几种故障形式，即卡死、恒增益故障、恒偏差故障以及漂移故障等.目前广泛使用的传感器故障方法仅仅通过判断传感器数据是否越限来进行故障检测，这种方法的优点是简单，但缺点也是过于简单，经常引起传感器故障的误判和漏判.

核动力装置是一个大型的热工水力系统，一回路冷却剂将反应堆堆芯发出的热量带出，通过蒸汽发生器传递给二回路水，产生蒸汽推动汽轮机做功.热力系统传感器具有很强的相关性，体现了设备本身的运行规律.该规律不仅与质量守恒和能量守恒等物理定律有关，也与运行规程或运行人员的操作习惯有关［1］，主元分析（principle component analysis，PCA）是一种对大量数据进行统计分析的方法，其用于传感器故障检测的基本思想是利用过程变量间的相关关系，建立正常工况下的主元模型，通过检验新的数据样本相对于主元模型的背离程度，从而发现传感器故障.它可以将一个多指标的问题转化为较少的综合指标.这些较少的综合指标之间互不相关并能提供原有指标的绝大部分信息.另外，PCA 障检测方法不依赖于过程的数学模型，因此非常适合在难以建立精确数学模型的复杂系统的故障检测.

PCA 用于故障检测方法是建立在稳定工况的基础上，对于核动力装置这种经常变工况（稳定－过渡－稳定）的情形，采用某单一主元模型进行检测会产生模型不适用问题，容易出现误诊或漏诊.本文采用一种动态多主元模型的检测方法，用于变工况情况下传感器的故障检测.

1 主元分析方法

使用传统的PCA 方法进行故障检测的方法是：（l）获取某一工况下的稳态数据，得到变量的统计信息，包括变量均值向量、变量方差矩阵、协方差矩阵、负载矩阵等，并将变量进行标准化处理以便建立此工况下的PCA 模型；（2）在线利用PCA 模型计算平方预测误差Q 统计量和T2统计量检测故障.由于T2统计量代表的只是与主元显著相关的那些过程变量的信息，而Q 统计量则代表的是所有被监测变量的（误差）信息，更能反映故障情况.黄孝彬等［2］通过300 MW 锅炉给水系统数据进行分析，认为在进行故障检测时T2指标弱于Q 指标；另外，Dunia等［3］在进行传感器故障检测时，并没有采用T2指标，只使用了Q 指标，应用效果良好.再者，本文在在进行故障检测时先对工况进行判断，剔除过渡过程，传感器发生了故障的情况易于判断.因此，本文只采用Q 统计量进行故障检测.

Q 统计量定义为［4］

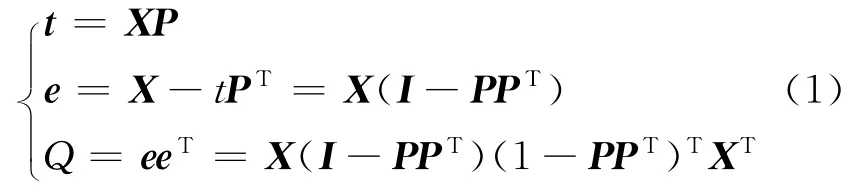
式中：X∈RN×m为标准化后的样本数据矩阵；P 为载荷矩阵，P＝［Pl，P2，…，Pn］，其列向量Pi为X的协方差矩阵的特征值λi所对应的单位特征向量，n为主元个数，t∈Rn是得分向量；I 为m×m的单位阵.给定一个显著性水平α，可以得到Q 统计量的控制限

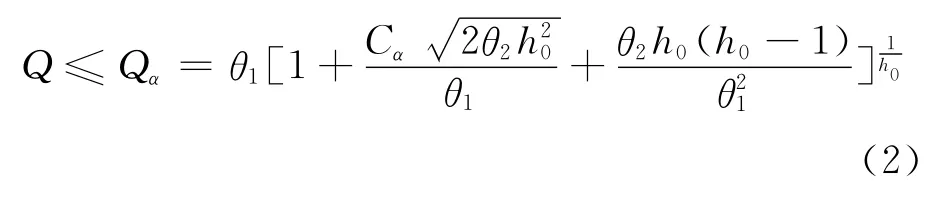
2 动态多主元分析方法

对于变工况的情形，采用某单一主元模型进行检测会产生模型不适用问题，这里主要表现为随着工况的变化，变量的均值，方差变化明显，如二回路蒸汽发生器给水流量、蒸汽流量、蒸汽压力等；另外随着工况变化，变量之间的相关性（表现为协方差）也随之发生变化.因此，采用动态多主元模型进行传感器的故障检测：（1）用模糊C－均值聚类方法［5－7］对过程的历史数据进行分类，得到各稳定工况下的正常历史数据；（2）利用分类数据建立相应的主元模型；（3）在故障检测中，首先利用稳定性因子分析方法［8］判断是否为稳态工况，如果处于过渡过程工况则停止检测；（4）当过程进入一个稳态工况后，根据模糊系统动态计算出一个与当前工况匹配的主元模型，并对检测样本进行故障检测.

2.1 主元模型组的建立

给定一个涵盖大部分工况的历史数据X∈RN×m（假设都已标准化处理），假设其包含W 个稳态工况和G 个过渡工况，通过稳定性因子判别去掉过渡工况，然后用模糊C－均值聚类方法将保留的稳态数据按照工况分成W 个不同的子集，用W 个子集建立W 个不同的主元模型，按照工况的高低构成一个主元模型组.一个主元模型对应一个稳态工况，因此，相对于单一主元模型，主元模型组可以更全面的描述整个过程.下面给出稳定性因子的定义和模糊C－均值聚类的方法介绍.

对于给定的变量Z，稳定性因子方法定义如下

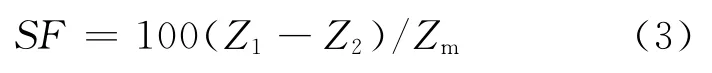
式中：Z1为变量Z 在一滑动窗口内的最大值；Z2为最小值；Zm为样本数据的均值.当稳定性因子较小时表明处于稳定状态，当稳定性因子较大时则处于过渡状态.计算过程中，取SF 的阈值为2.

假设稳态工况的样本数为H，模糊C－均值聚类的目的是把稳态工况下的H 个样本划分到C个类别中去，使各样本与其所在类的均值的误差平方和最小.C－均值聚类算法需要事先给出期望的分类数目，一般情况下这个条件比较难满足，然而对于工况的数据分类可以根据特征变量的分析比较容易得到需要分类的数目.

定义聚类的一般目标函数描述为

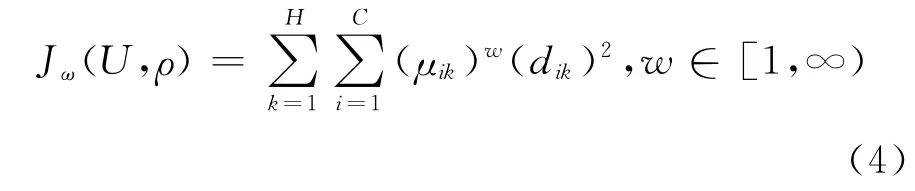
式中：μik＝μXi（xk）为样本xk与子集Xi（1≤i≤C）的隶属关系；w 为加权指数，一般取2.dik为样本与第i类的聚类中心ρi 之间的距离

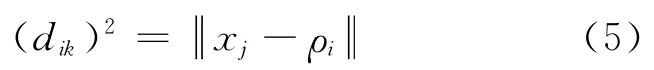
聚类准则为取Jω（U，ρ）的极小值min｛Jω（U，ρ）｝，使得Jω（U，ρ）为最小的μik值为

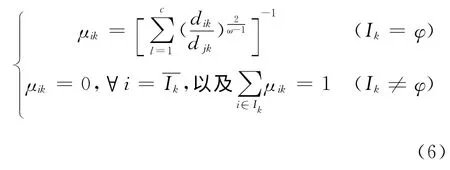
式中：Ik＝｛i｜dik＝0｝，使得Jω（U，ρ）为最小的ρi值为

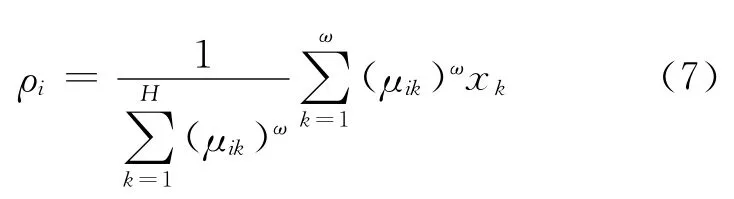
2.2 动态PCA在线故障检测

在工况的过渡过程中变量的统计特性会发生较大变化，这时使用稳态工况下建立的主元模型进行故障检测必然带来误诊.因此在故障检测过程中必须先判定过程的运行状态，如果处于工况的过渡过程中则停止检测并将统计量赋值为零，待过程进入稳态工况后继续进行检测.使用负荷指令变量的稳定度因子来判断过程的状态.

当过程处于稳态时，需要根据当前工况为新检测样本匹配一个合适的主元模型来进行检测.主元模型匹配的过程依据样本对所划分类的隶属度来判别，其过程如下［9］：（1）样本矩阵的标准化，将数据变换到［0，1］区间，采用平移－极差变换；（2）建立样本的模糊相似矩阵，采用相关系数法；（3）聚类，采用直接聚类法，当样本对某类的隶属度大于0.8时则划分为该类.

然后用得到的动态主元模型中的均值向量和方差矩阵对检测样本进行标准化，使用动态主元模型中的负载矩阵和协方差矩阵按照式（1）计算Q 统计量，进而实现故障检测.

3 应用实例

核动力装置的运行过程是典型的变工况过程，其工况随负荷的变化不断变化，以核动力装置连续升负荷系统为例说明多主元模型在核动力装置传感器故障检测中的应用.反映核动力装置运行的参数主要有26个，见表1.

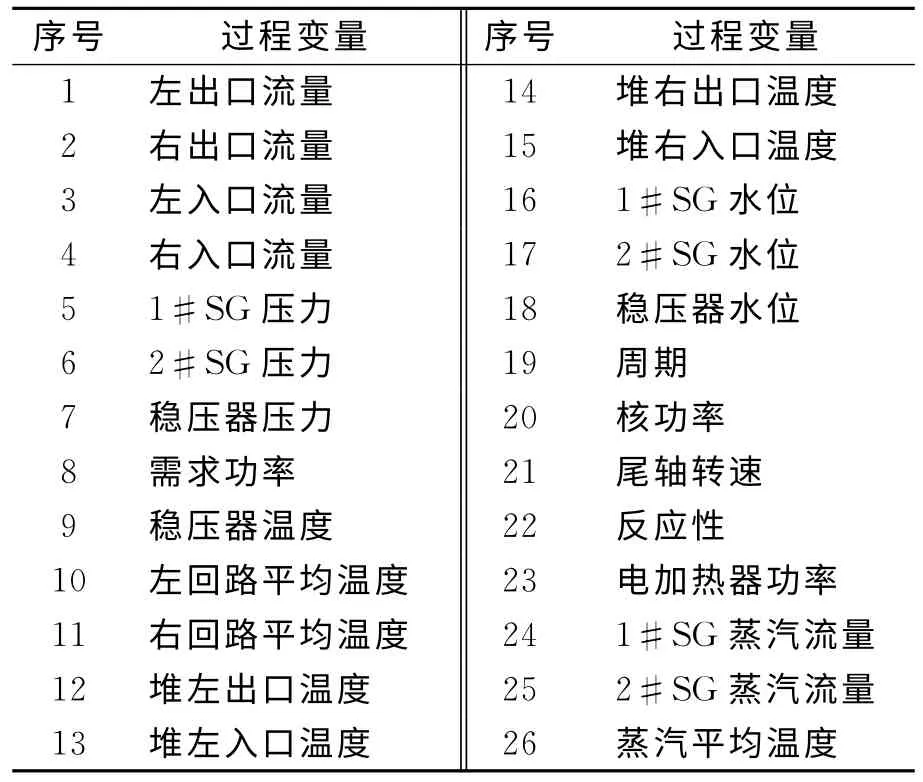
表1 主要过程变量

选取一段时间的连续运行数据作为建模数据，采样间隔为1s，工况特征变量选择核功率、蒸汽流量、尾轴转速.先对数据进行分类得到5类数据样本集，分别为样本集1、样本集2、样本集3、样本集4和样本集5，分别对应工况2，工况3，工况4，工况，5和工况6等运行工况，并建立相应的主元模型.选取一段包含工况变化的连续运行数据，其包含5个稳态工况和5个过渡过程，其归一化数据的变化趋势见图1.

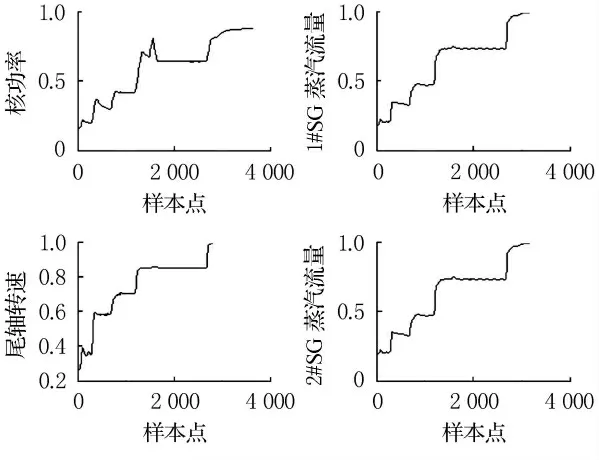
图1 工况特征变量变化趋势图

尾轴转速这一特征变量的稳定性因子最能表征工况的变化，稳定性因子变化见图2.从图中可以看出，稳定工况下其稳定性因子小于2，过渡过程的稳定性因子较大.剔除掉过渡过程工况，只保留稳态工况下的数据，并将其分类，聚类的目标函数变化趋势见图3.

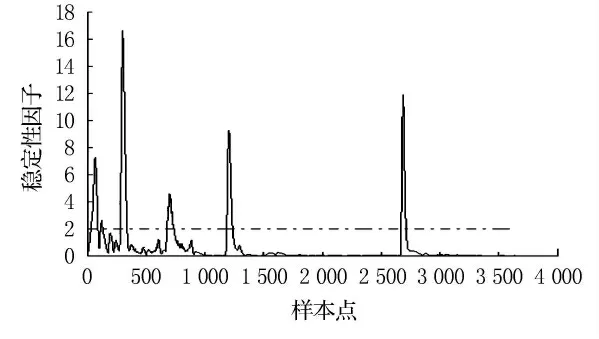
图2 变工况的稳定性因子变化趋势

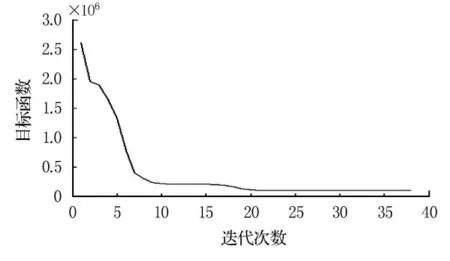
图3 目标函数的变化趋势

下面通过实验检验该方法的有效性.

试验1在过程运行正常时，检验过渡过程工况对检测结果的影响，见图4.经计算的PCA分析过程中，最大的4个特征值分别为16.6527，5.3028，2.1900，0.9986，所有特征值的和为26.0000，其主元贡献率为96.71%，当贡献率超过85%时候即可取其为主元，考虑到计算复杂程度与数据的代表性，取主元个数为4.

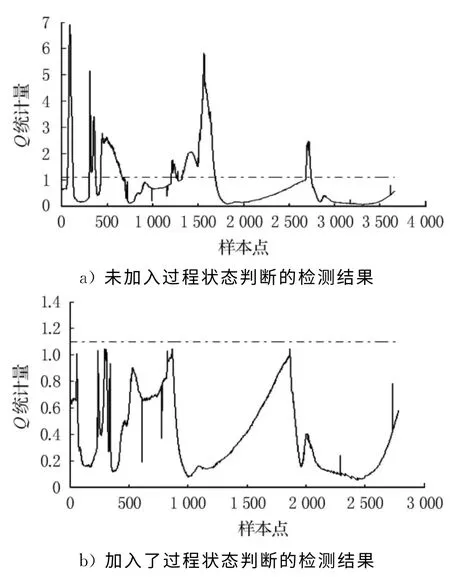
图4 过渡过程对检测结果的影响

图4a）为未考虑过渡过程时的检测结果，其中虚线为置信度为99%时统计量的控制限值.图4b）为考虑过渡过程的监测结果.从图4a）中看出，正常情况下，未加入对过渡过程的判断，出现了误诊；从图4b）中看出，在加入了过渡过程判断后，诊断结果正常，避免了误诊.

试验21＃SG 蒸汽流量（随工况的变化而变化）传感器出现故障时的检测结果，在第500个采样点时在蒸汽平均温度上叠加5%的恒偏差来模拟传感器故障.检测结果见图5.

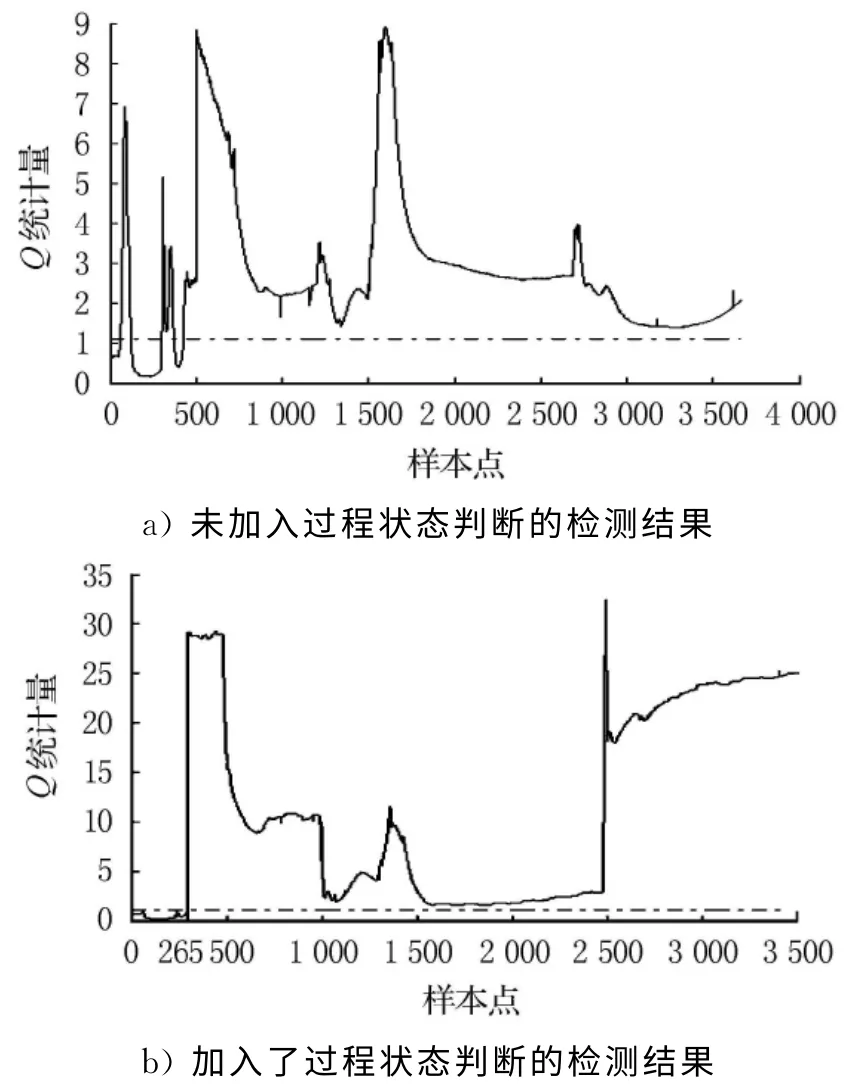
图5 蒸汽流量传感器发生故障后的检测结果

从图5a）中可以看出，未加入过程状态判断时，前500个采样点虽然为正常状态但是出现了误诊，后面的采样点则检出了故障状态；从图5b）常数据的采样点数据只有265个，检测结果为正常，叠加了故障后，由于去除了过渡过程，数据也有所减少，故障被检测出来.并且比较图5a）和图5b）可以知，由于采用了动态主元模型，发生故障时对故障的检测更灵敏，反映在图中就是图5b）中Q 的幅值比图5a）的更大.

4 结束语

变工况情况下，传统的PCA 模型用于传感器的故障诊断存在模型不适应问题，利用PCA 的Q统计量进行检测，过渡过程情况下容易出现误诊断；对过程进行稳定性分析剔除掉过渡过程后将数据进行分类，利用动态多主元分析方法根据数据类型的不同建立不同稳态工况下的主元模型，使得模型更适应不同的工况，不会出现误诊；由于模型更适应实际工况，对故障的检测也更灵敏.

该方法虽然解决了不同稳态工况的模型适应问题，但前提是剔除了过渡过程，对于过渡过程中传感器的故障检测问题依然没有解决，有待进一步研究.

［1］RICARDO H D，JOE Q S，THOMAS F E.Multivariable process monitoring using nonlinear approaches［C］／／Proceedings of the American Control Conference，1995：756－760.

［2］黄孝彬，牛 征，牛玉广，等.利用主元方法进行传感器故障检测的行为分析［J］.传感技术学报，2003，16（4）：419－423.

［3］RICARDO H D，JOE Q S，THOMAS F E，et al.Identification of faulty sensors using principal component analysis［J］.AICHE Journal，1996，42（10）：2797－2812.

［4］孙娇华.基于主元分析传感器故障检测、辨识与重构的研究［D］.沈阳：沈阳化工学院，2003.

［5］陈 凯，朱 杰，王豪行.复杂系统故障诊断中的模糊聚类方法［J］.上海交通大学学报，1998，32（6）：61－64.

［6］刘建敏，刘艳斌，乔新勇，等.基于模糊聚类与神经网络的柴油机技术状态评价方法研究［J］.内燃机学报，2008，26（4）：379－383.

［7］闻 新，周 露，李东江，等.Matlab模糊逻辑工具箱的分析与应用［M］.北京：科学出版社，2001.

［8］DORR R，KRATZ F，RAGOT J.Detection，isolation，and identification of sensor faults in nuclear power plants［J］.IEEE Trans on Control Systems Technology，1997，5（1）：42－60.

［9］谢季坚，刘承平.模糊数学方法及其应用［M］.武汉：华中科技大学出版社，2006.