自适应线谱增强算法改进及其在轴频电场信号检测中的应用＊

胡 鹏龚沈光 蔡旭东

（海军指挥学院信息战研究系1） 南京 211800） （海军工程大学兵器工程系2） 武汉 430033） （海军91388部队92分队3） 湛江 524022）

0 引 言

船舶轴频电场是因船舶主轴转动而调制腐蚀或防腐电流产生的一种以螺旋桨转动频率为基频的极低频电场.该电场具有明显的线谱特征和谐波成分，其基频为1～7Hz.另外，该电场有着足够可测量的强度，因而可以作为水中探测的理想信号源［1－2］.但由于海水的导电性，轴频电场信号在海水中随着传播距离的增大变得极其微弱［3］，给远程探测带来了困难.因此，研究低信噪比情况下轴频电场信号的线谱检测算法具有重要意义.

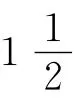
1 线谱检测算法

自适应线谱增强（adaptive line enhancement，ALE）算法是在加性噪声中对线谱进行参数估计的自适应谱估计技术，可用于检测窄带信号.在窄带信号加上宽带信号的情况下，无需独立的参考信号，将混合信号进行延迟，延迟的作用是使宽带信号去相关，而窄带信号不去相关，利用最小均方自适应滤波器，自适应地与相关的窄带信号进行匹配，从而将信号分离出来［7］.

自适应线谱增强算法的原理框图见图1［8］.

其计算公式如下.

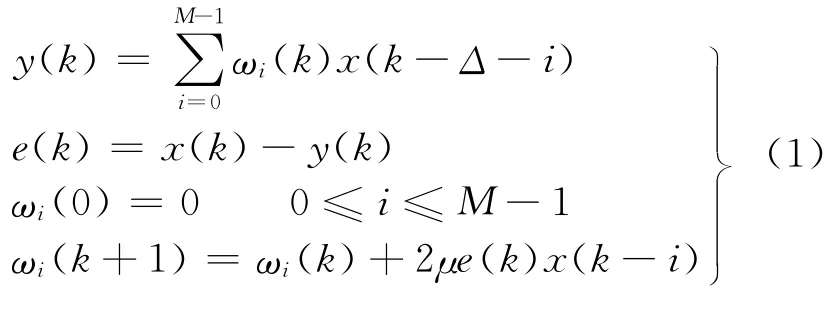
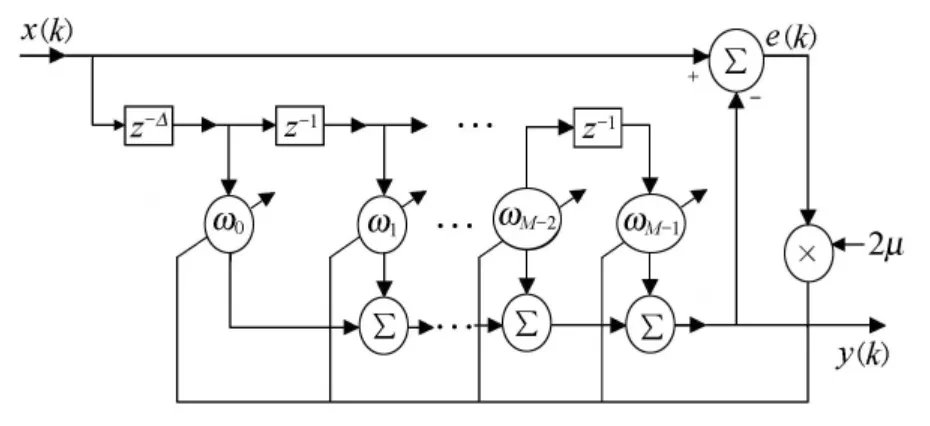
图1 自适应线谱增强算法

式中：M 为自适应滤波器阶数；μ 为自适应学习步长.

由于采用LMS自适应算法的线谱增强器存在迭代噪声，因而其处理增益在输入信噪比较低时性能较差.文献［9］证明了自适应线谱增强的延时线和自适应滤波器等效于2π整数倍的相移器，并提出采用相干累加技术来改进自适应线谱增强的性能.由于在累加过程中，信号分量将同相相加，而干扰分量只是能量相加，因而取得了一定的处理增益.为了充分利用误差更多的历史信息，使误差信息更接近于真实值，从而进一步消除迭代噪声的影响.本文在用相干累加算法改进自适应线谱增强的基础上，提出了一种改进的自适应线谱增强算法，其原理图见图2.

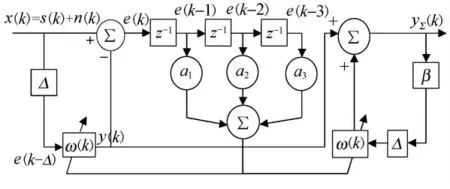
图2 改进的自适应线谱增强算法

其计算公式如下：

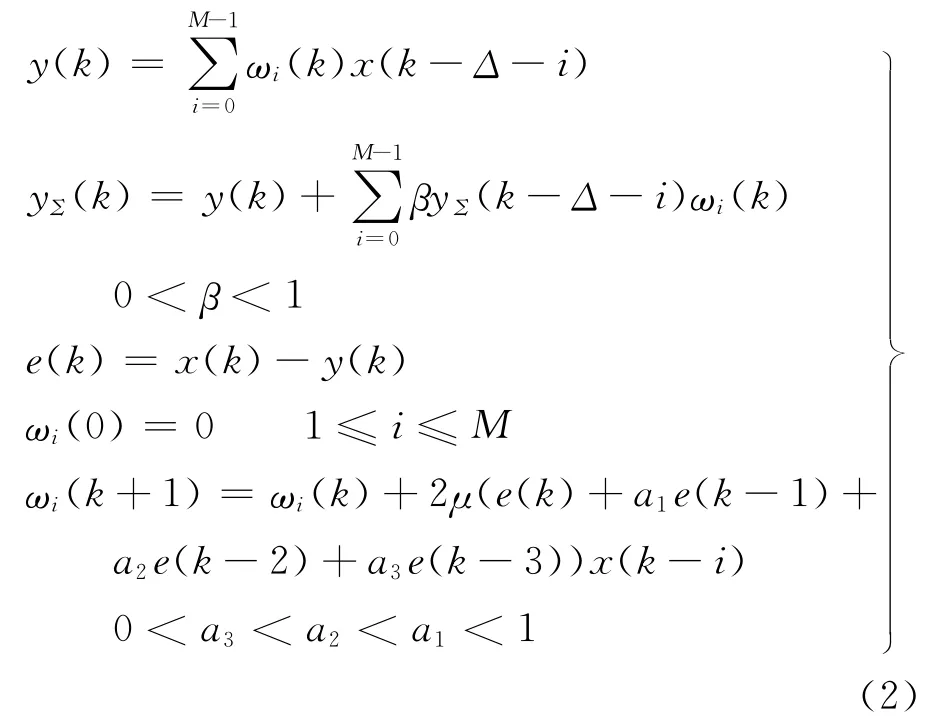
式中：β为常数，通常取0＜β＜1来保证系统的收敛性.

通过式（2）可以得出改进的ALE 的z 变换HΣ（z）为

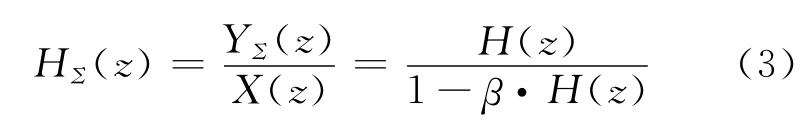
式中：H（z）为横向滤波器和延时线Δ 的z 变换.

由式（3）可知，改进的ALE 具有ARMA 结构的滤波器性能，因而与横向滤波器相比有很窄的通带和更强的过滤噪声的能力，从而提高了系统的处理增益.另外，由于改进的ALE 不仅利用当前的误差信息，而且还利用了前几次的误差信息，几个输出误差线性组合大大消除了迭加噪声的影响，因而可进一步提高处理增益.

2 算例实验及结果分析

为验证算法的有效性，并比较不同信噪比条件下本文方法与普通的自适应线谱增强算法的性能，分别使用实测数据和仿真数据对上述两种方法进行检验.确定两种检测方法的主要参数如下：M＝128，μ＝0.0001，延时Δ＝15s，β＝0.8，系数a3＝0.5，a2＝0.2，a1＝0.05.

2.1 实测数据处理结果

海上实验于2007年4月在我国东海某海域进行.测量期间，海面状况为小浪，海况为二级.实验时测量体位于航道下方15.4 m 水深处，采样频率为25Hz，实测数据在被采集之前都经过了1～7Hz的模拟滤波.目标船舶为某货船，船舶通过时距离水下测量体正横距离为25m 左右.图3所示为目标船舶通过时的轴频电场垂直分量信号及其频谱图，该船通过时间约为25s.

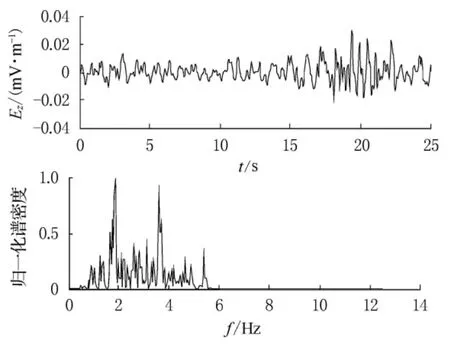
图3 实测船舶轴频电场信号垂直分量及其频谱图

由图3 可知，所测轴频电场信号相对海洋环境电场信号较强.从图中可以看出轴频电场信号的基频约为1.8 Hz，且包含其二倍频等谐波成分.

分别采用普通的自适应线谱增强算法和本文算法对上述实测信号进行处理，处理后的信号频谱图如图4所示.其中，图4a）为普通ALE 处理结果，图4b）为本文算法处理结果.

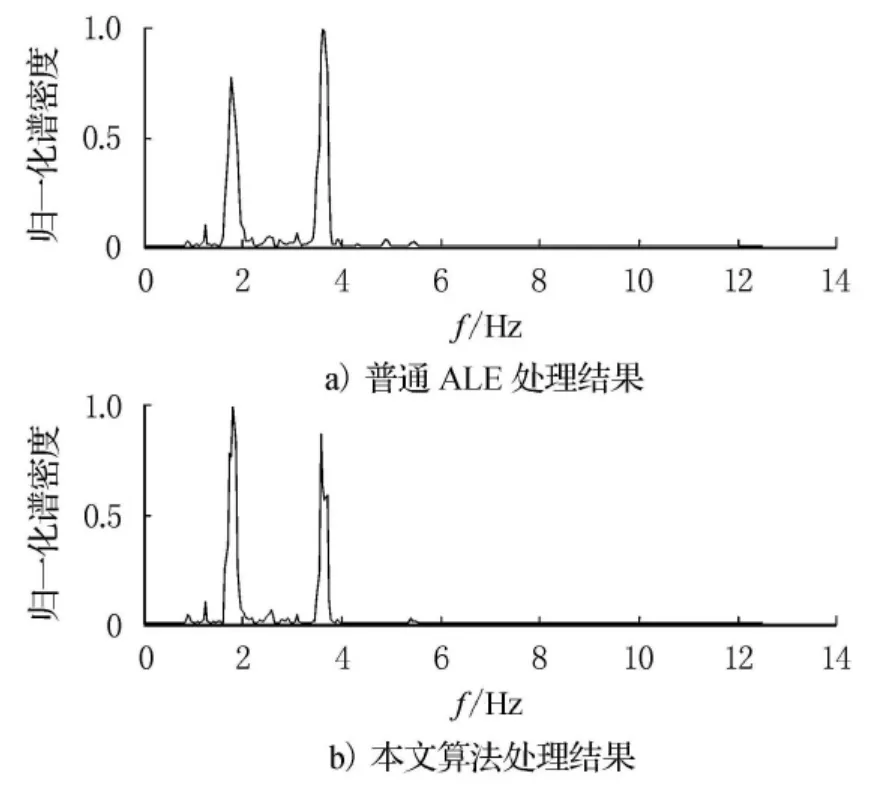
图4 2种算法对实测信号的处理结果

由图4可知，在信噪比较大的情况下，两种算法均能有效地从海洋环境电场中提取轴频电场信号的线谱.

2.2 仿真数据处理结果

由于本次实验未获得复杂海况下的船舶轴频电场数据，为检验本文算法在低信噪比条件下的线谱检测效果，本文利用仿真数据对其进行检验.仿真数据由作为信号的实测船舶轴频电场的纵向分量和作为噪声的实测海洋环境电场的纵向分量通过线性叠加产生.其中，信号由长基线传感器在船舶附近测得，具有很高的信噪比.通过对噪声乘以不同的系数来调节信噪比，信噪比的计算公式为SNR＝10lg（Es／En）.式中：Es和En分别为信号总能量和噪声总能量.

图5所示为长基线传感器测得的船舶轴频电场纵向分量及其频谱图，从图中可以看出该信号的基频约为1.8Hz，且包含其2倍频及3倍频等谐波成分.

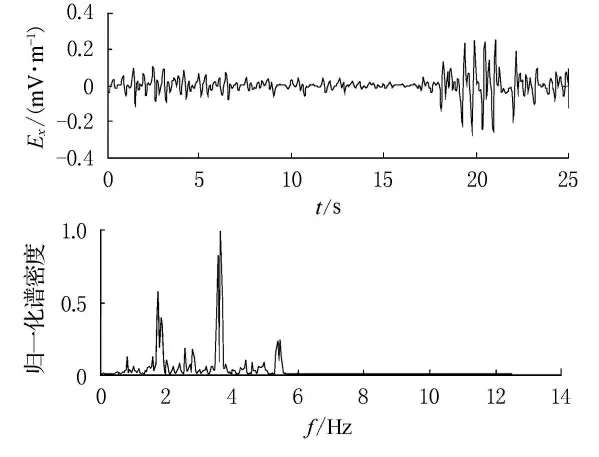
图5 实测船舶轴频电场信号纵向分量及其频谱图

将作为噪声的实测海洋环境电场纵向分量加在图5所示的信号上，调节噪声系数为30，得到一组信噪比约为－6dB的混合信号，其频谱图如图6所示.

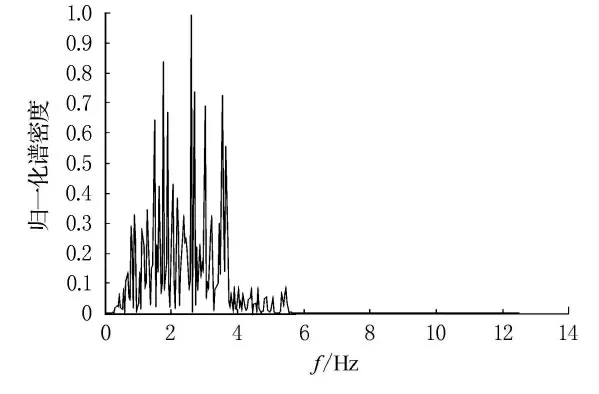
图6 SNR＝－6dB时仿真观测信号的频谱图

由图6可知，当信噪比为－6dB时，轴频电场信号已完全被海洋环境电场所掩盖，从图中并不能看出轴频电场信号的基频及其倍频等谐波成分.

分别采用普通的自适应线谱增强算法和本文算法对上述仿真观测信号进行处理，处理后的信号频谱图见图7.

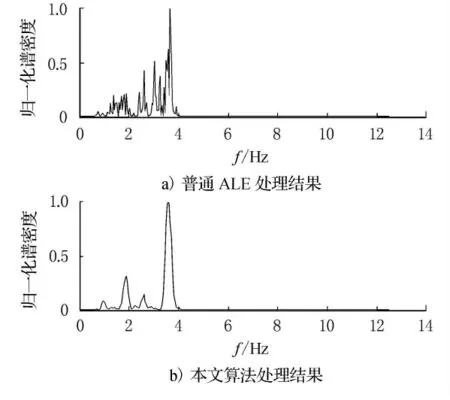
图7 2种算法对仿真信号的处理结果

由图7可知，当信噪比降至－6dB 时，普通的自适应线谱增强算法已经不能从海洋环境电场噪声中提取出轴频电场信号的基频，而改进的自适应线谱增强仍能有效地对淹没在噪声中的轴频电场信号的线谱进行检测，提取出其基频及2倍频等谐波成分.

3 结束语

本文对自适应线谱增强算法进行了改进，即在增加相干累加算法的基础上，对几个输出误差进行加权处理，使得越接近当前时刻的误差其权值越大，从而使误差信息更接近于真实值.实测数据和仿真数据处理结果表明，在低信噪比情况下，本文算法较普通自适应线谱增强算法能更有效地检测到目标信号的线谱，为船舶轴频电场信号的线谱检测提供了新的途径.

［1］林春生，龚沈光.舰船物理场［M］.北京：兵器工业出版社，2007.

［2］龚沈光，卢新城.舰船电场特性分析［J］.海军工程大学学报，2008，20（2）：1－4.

［3］Applied Physics Laboratory，University of Washington.Electrode and Electric Field Sensor Evaluation［R］.San Die go：SPAWAR Systems Center，2001.

［4］FCO J R，ANTONIO S.Using electric signatures for extracting target navigation parameters［C］／／Undersea Defence Technology，Amsterdam：C Martin，1999：12－18.

［6］卢新城，龚沈光，林春生.自适应谱线增强在舰船轴频电场信号检测中的应用［J］.数据采集与处理，2004，19（4）：438－440.

［7］GHO M.Analytic behavior of the LMS adaptive line enhancer for sinusoids corrupted by multiplicative and additive noise［J］.IEEE Transactions on Signal Processing，1998，46（9）：2386－2393.

［8］Simon Haykin.自适应滤波器原理［M］.郑宝玉，译.北京：电子工业出版社，2006.

［9］侯宝春，惠俊英，蔡 平.用相干累加算法改进ALE的性能［J］.声学学报，1991，16（1）：25－30.