非均匀磁场中Heisenberg XXZ自旋链的热量子失协*
(武汉理工大学理学院 武汉 430070)
0 引 言
量子纠缠是一种量子关联,在量子通信和信息处理如量子编码、量子态隐形传态、量子密钥分配和量子计算中起着举足轻重的作用[1].随着研究的深入和理论及应用的需要,人们发现量子纠缠仅仅是一种特殊的量子关联,并没有完全刻画经典关联与量子关联的本质区别,于是比量子纠缠更一般的的量子关联现象的研究变得迫切起来.2001年H.Oliveier和 W.H.Zurek提出了量子失协(quantum discord,QD)这个概念[2],用于量化量子关联.量子失协,它是用来量化系统中的所有非经典关联.据观察,量子失协是更一般的量子关联度量,它可能包含一个独立的量子纠缠.此外,量子失协给非经典关联提供一个更大区域的量子态,并且提供一个非零值的量子关联.这种量子关联不是量子纠缠,而是比量子纠缠更一般的量子关联-量子失协.
近十年来量子失协已在许多方面受到重视,如热力学和关联、量子计算、失协的动力学等.特别是,一些文献研究了在不同的海森堡模型中的热纠缠和量子失协[3-5].结果表明:对于在有限温度时热量子失协比热纠缠更强大,因为量子失协在有限温度下不会消失,但热纠缠在一定温度下完全消失.所以在描述量子关联时量子失协比量子纠缠更实际,而且基于量子失协的量子算法比那些基于量子纠缠的算法更强大.介于此目的,本文研究了在非均匀磁场中两量子比特的一维海森堡XXZ自旋链的热量子失协,通过比较其量子失协和量子纠缠,探讨二者之间存在的差异.
1 量子失协和量子纠缠
为了描述量子关联,采用两种类型的度量,包括concurrence和量子失协.由 Wootters[6]定义的concurrence是计算2个量子比特混合态ρAB的形成纠缠度.它可以由C=max}表示.式中:物理量λ1,λ2,λ3,λ4分别是矩阵R=ρAB(σy⊗σy)ρA*B(σy⊗σy)按降序排列的本征值.C=0对应于没有纠缠态,而C=1为最大纠缠态.
另一方面,在经典信息理论中,对于任意的二分态,2个子系统之间的总关联可以用量子相互信息来描述[7],有
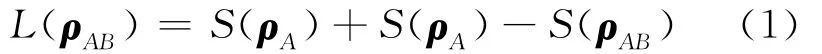
式中:S(ρ)=tr(ρlbρ)是冯·诺伊曼熵,ρA(B)=trB(A)ρ是通过追踪系统B(A)的约化密度矩阵.量子相互信息具有基本物理的重大意义,它通常被用来度量包含量子和经典的总关联.对于子系统A和B的经典关联可以定义为
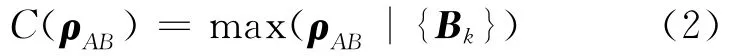
式中:L(ρAB|{Bk})是在量子系统B 上的一个基于给定度量基{Bk}的量子相互信息的变量,即

式中:ρk=(Ik⊗Bk)ρAB(Ik⊗Bk)/pk是在得到结果k在B 的概率pk=tr[(Ik⊗Bk)ρAB(Ik⊗Bk)]之后对A投影度量态,Ik是子系统A 的恒等运算.当子系统B中描述二维希尔伯特空间{|0〉,|1〉}时,局部度量的完全集由{Bk=V|k〉|k〉V+,(k=0,1)}给出,这里任意幺正变换V(θ,φ)(其中θ∈[0,π],φ∈[0,2π])为
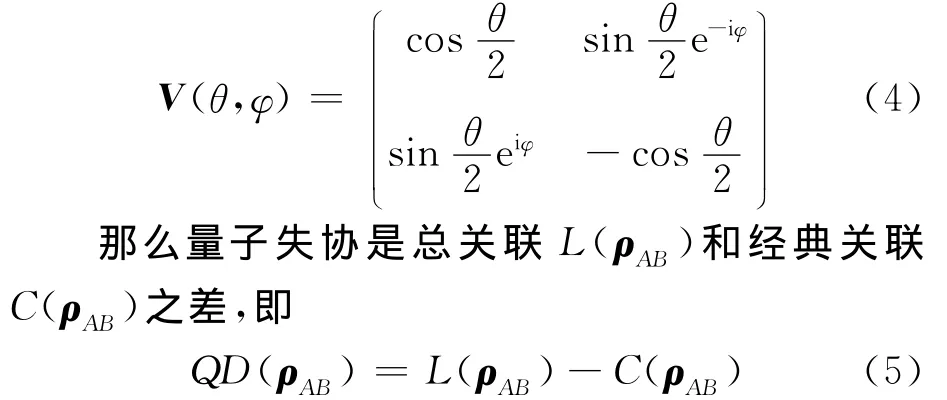
2 结果及其讨论
非匀强磁场中各向异性的2量子比特-维海森堡XXZ自旋链的哈密顿量为
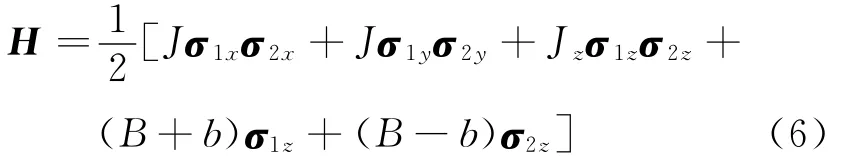
式中:J和Jz为自旋耦合系数,J>0和Jz>0对应反铁磁情况,而J<0和Jz<0对应铁磁情况;B为Z方向上均匀磁场;b为Z方向上的非均匀磁场,b值控制其非均匀磁场的梯度,并且σi(i=x,y,z)是泡利矩阵.
密度矩阵ρAB=exp(-H/kT)/Z描述在温度为T 下的热(正则系综)平衡系统.式中:Z=tr{exp(-H/kT)}是一个配分函数;k是玻耳兹曼常数,为了简单起见,假定k=1.因此,在基矢{|00〉,|01〉,|10〉,|11〉}中,式(6)具有以下形式

通过哈密顿量H可以得到这些非零矩阵元素的精确值为

通常情况下,量子失协难以计算,并且无法得到解析解.对于密度矩阵(7)描述的X状态,如果
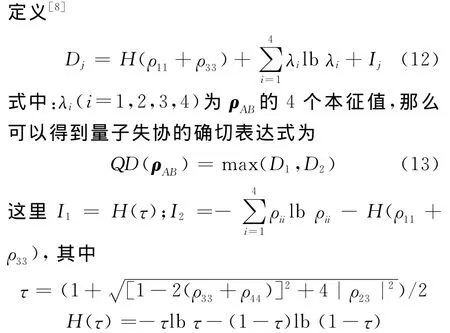
图1描绘了量子纠缠量子纠缠concurrence和量子失协QD在不同温度T下的关系.从图中可以看出,在以下3种情况下:(1)无外加磁场(B=0,b=0);(2)均匀磁场(B=2,b=0);(3)非均匀磁场(B=2,b=5),量子纠缠concurrence和量子失协QD都随温度T的增加而减小.这种行为的原因是最大纠缠态与其他态的混合而引起的.然而,显而易见的是,它们之间存在着一定的差异:量子纠缠concurrence的值在临界温度处下降到零时,而量子失协QD随着温度T渐近地下降到零.由于没有引进退相干,量子关联不会消失.所以在这个意义上说,量子失协在有限温度下比量子纠缠更强大,在量子计算和量子通讯中比量子纠缠更现实.从图1中还可以发现,外加磁场,不管是均匀的还是非均匀的,对量子纠缠和量子失协都有比较显著的影响.而且从图1a)中还可以看出,均匀磁场B并不能改变临界温度T的值,而非均匀磁场b可以增加临界温度T的值.从这一点可以得到:非均匀磁场在有限温度下有益于量子纠缠.(注:所有参数都为量纲一量化,图1~4中的所有参数都同样为量纲一量化.)
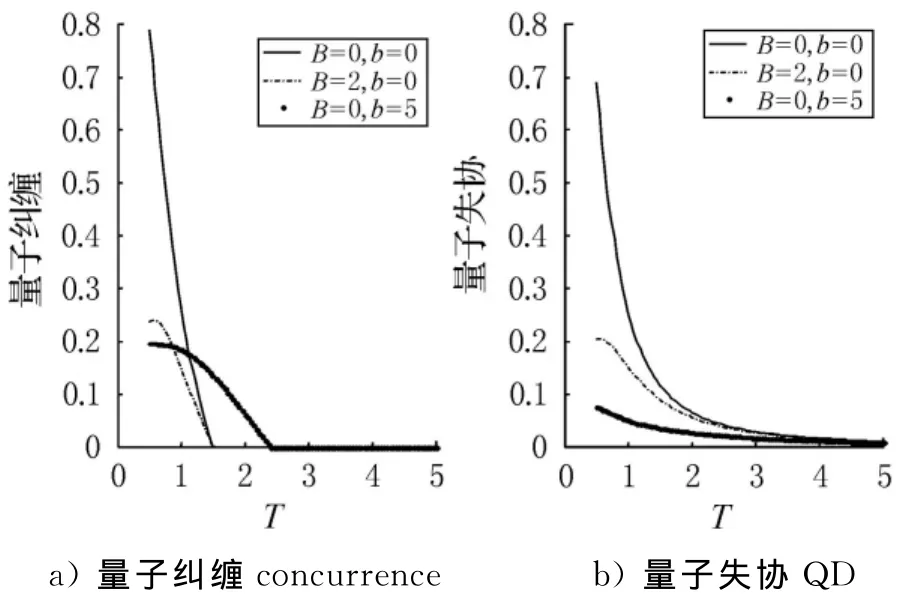
图1 与温度T的关系(J=1,Jz=0.5)

图2 与均匀磁场B的关系(J=1,Jz=0.5,b=0)
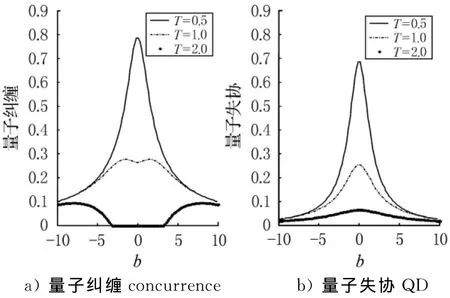
图3 与非均匀磁场b的关系(J=1,Jz=0.5,B=0)
接下来继续讨论外加磁场(均匀和非均匀)对量子纠缠和量子失协的影响.图2描述的是均匀磁场下的情况;图3描述的是非均匀磁场的情况.从图中可以看出:量子纠缠concurrence和量子失协QD都关于均匀磁场|B|和非均匀磁场|b|在零点处对称,但两者有明显的不同:(1)对于在均匀磁场情况下,如图2所示,无论温度T如何变化,量子纠缠concurrence和量子失协QD都随着|B|的增加而减小;当然在温度T超过温度临界点的时候,量子纠缠消失,其concurrence值为0,比如图2中的较高温度曲线T=2.0,而这种情况下在量子失协上不存在;(2)对于在非均匀情况下,如图3所示,在较低温度下,图3中的较低温度曲线T=0.5,量子纠缠concurrence和量子失协QD都随着|b|的增加而较小,两者的变化趋势是相同的.但随着温度T的增加,如图3所示,两者有明显的差别:量子失协QD依然随着|b|的增加而减小,而量子纠缠concurrence随着|b|的增加先增加到最大值,然后再随着|b|的增加而减小,concurrence最初值甚至从0开始.因此可以找到一个在量子纠缠concurrence增加而量子失协QD减小的区域,甚至是没有量子纠缠而量子失协依然存在的区域.这是一个非常有趣的现象,可以理解为:在温度T达到一个合适的值时,一个合适的外加场可以部分消弱热涨落的破坏性影响而增强量子纠缠.
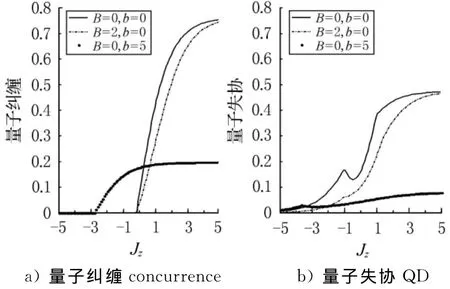
图4 与自旋耦合系数Jz 的关系(J=1,Jz=0.5,T=1.0)
最后讨论在不同磁场情况下量子纠缠concurrence和量子失协QD与自旋耦合系数Jz的关系.从图4a)中,无论是有无外加磁场,或外加磁场无论是是均匀的还是非均匀的,都可以发现:当Jz从正值到负值变化时,其量子纠缠concurrence的值也在减少,并在Jz的临界值时,下降到0.同时增加非均匀磁场b的值时,可以增加|Jz|的临界值.但在无外加非均匀磁场的情况下,均匀磁场的增加并不能改变|Jz|的临界值.从图4b)中,很容易发现:在无外加磁场的情况(B=0,b=0)下,量子失协QD在|Jz|=±1处产生突变,这表征在此处发生量子相变,即使是在有限温度下(通常量子相变发生在T=0处).因此,与图4a)相比,在有限温度下,可以用量子失协QD来检测量子相变,而量子纠缠concurrence却不能.可见,量子失协QD对于在实验上检测量子相变有重要意义.在有外加磁场(无论是均匀还是非均匀)的情况下,量子失协发生突变的Jz的临界值向Jz>1或者Jz<-1两端变化,这表明量子失协依然可以用来检测量子相变.但随着外加磁场的增加,可以发现,量子失协QD的突变在渐渐消失,这表明量子相变会在外加磁场的影响下消失.
3 结束语
本文研究了外加非均匀磁场下一维两量子比特Heisenberg XXZ自旋链中的热量子失协,讨论了温度T和外加磁场(包括均匀磁场和非均匀磁场)对其量子失协的影响,并比较了量子纠缠和量子失协两者之间的差异.结果表明:在相同的物理参数范围中,导致量子纠缠猝死的这些因素仅仅加速量子失协的衰变,而当量子纠缠消失时,量子失协会呈现无限趋近于0而不会消失的现象.因此,量子失协在退相干环境下比量子纠缠更强大,在量子关联度量中比量子纠缠更普遍,在量子计算和量子通信中比量子纠缠更实用.
[1]NIELSEN M A,CHUANG I L.Quantum computation information[M].Cambridge:Cambridge University Press,2000.
[2]OLLIVIER H,ZUREK W H.Quantum discord:a measure of the quantumness correlations[J].Phys.Rev.Lett.,2001,88:017901-1-4.
[3]WERLANG T,RIGOLIN G.Thermal and magnetic quantum discord in Heisenberg models[J].Phys.Rev.A,2001,81:044101-1-4.
[4]WERLANG T,TRIPPE C,RIBEIRO G A P,et al.Quantum correlations in spin chains at finite temperatures and quantum phase transitions [J].Phys.Rev.Lett.,2010,105:095702-1-4.
[5]GUO J L,MI Y J,ZHANG J,et al.Thermal quantum discord of spins in an inhomogeneous magnetic field[J].J.Phys.B:At.Mol.Opt.Phys.,2011,44:065504-1-6.
[6]WOOTTERS W K.Entanglement of formation of an arbitrary state of two qubits[J].Phys.Rev.Lett.,1998,80:2245-2248.
[7]GROISMAN B,POPESCU S,WINTER A.Quantum,classical,and total amount of correlations in a quantum state [J].Phys.Rev.A,2005,72:032317-1-11.
[8]WANG C Z,LI C X,NIE L Y,et al.Classical correlation and quantum discord mediated by cavity in two coupled qubits [J].J.Phys.B:At.Mol.Opt.Phys.,2011,44:015503-1-9.

