基于STBC的混沌MIMO雷达的信号处理研究＊

0 引 言

MIMO（multiple input multiple output）通信系统可以克服无线信道衰落效应，对于独立的多径衰落，MIMO通信接收机的平均信噪比几乎保持不变．受此启发，2004年美国学者Fishler等首次提出 MIMO雷达的概念［1］．MIMO雷达使用多个发射天线同时发射独立的信号波形照射目标，并使用多个接收天线接收目标反射的信号．因此对目标的RCS（雷达散射面积）起伏不敏感［2］．此外，MIMO雷达可以实现灵活的发射分集设计［3－4］，具有高 分 辨 率 的 空 间 谱 估 计 性 能［5］．MIMO雷达在布阵上主要分两大类：紧凑型和分布式［6］．紧凑型的分布类似于相控阵雷达，通过发射正交信号，采用低增益的宽波束照射探测空域，大大提高目标的检测能力，因而不同于属于传统意义上的相控阵雷达；而分布式则相当于多基地雷达，利用多个不同方位的雷达发射信号，较好地克服了目标RCS的角闪烁所带来的性能损失，获得较大的空间分集增益，能够根据多普勒频移解决慢目标的检测问题，而且能够克服带宽的限制实现更高精度的目标定位．从目前研究情况来看，大多假设MIMO雷达发射天线是稀疏布阵．寻求一种优化的MIMO雷达的收发分布，建立相应的数学模型，可进一步提高它的检测性能．

目前很多学者对MIMO雷达发射的正交信号进行了研究和设计，都在研究如何形成相互正交的波形．已经提出来作为MIMO雷达发射的波形有：多相码，OFDM，正交跳频编码，BPSK，正交频分LFM，Costas码，随机序列码，正交恒包络OFDM 波形设计［7］，OFDM－LFM，混沌调频信号等．然而能够做到严格意义的正交比较困难，本文将MIMO通信中的STBC编码应用于雷达中，主要提出了使用超宽带混沌信号作为发射的波形，再由STBC形成严格意义上的正交波形，并设计了在接收端使用相关处理方法，最后根据整个雷达系统，推导出了其目标检测的公式．

1 超宽带混沌信号的STBC编码原理

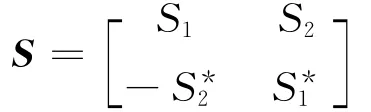
以较为简单2X1正交空时分组码为例，它采用2根发射天线和1根接收天线，其发射矩阵为即在第一个发射周期中，信号S1和S2同时从天线1和2发射．在第二个发射周期中，信号－从天线1发射，而从天线2发射出去．其中：和分别为S1和S2的复共轭，而对于实数信号就是它本身．发射信号的矩阵满足：

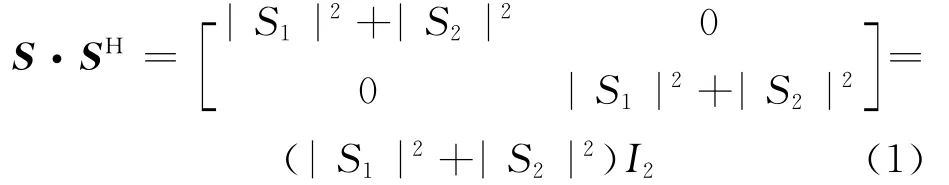
满足正交特性，所以从2根天线上发送出去的信号是严格正交的［8］．这是最简单的发射天线为2的情况，S为2×2的正交方阵，对于实正交设计而言，并非可以任意选取发射天线数．

对于发射信号为方阵时，当且仅当发射天线数 M＝2，4，8，实正交设计才存在［9］．

该理论对于设计空时编码的MIMO雷达系统具有一定的指导意义，在M 为方阵时，其正交设计并不惟一．也可以对实正交矩阵的设计进行推广，如果发射矩阵不限于方阵，同样也可以构造出任何发射数的实空时分组码，且满速率和时延最优．

现将这一理论用于2×2的雷达系统中．

二相编码雷达信号因具有截获概率低、抗干扰能力强的优点，因而获得了广泛应用．同时由于混沌信号具有类随机和对初值敏感、易于产生的特性，在此，选用混沌量化处理后的信号作为二相码，码长的选取更具灵活性，同时也增强了系统的安全性．依靠二相混沌序列码对宽发射脉冲进行调制，在接收端通过匹配滤波可以得到高的距离和速度分辨力．

首先使用Logistic混沌映射产生混沌二相码［10］．

Logistic映射的迭代表达式为

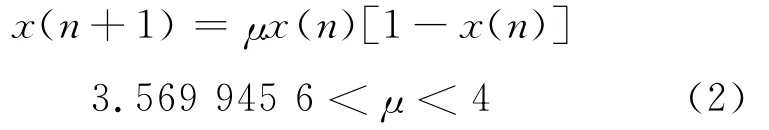
选取Lyapunov指数大的序列，在产生了1 000个序列之后，选取N（N＝20）个，求其均值E，再进行量化处理，规则如下：

在Matlab软件环境下，经过多次仿真实验，选取了下面的这组序列，虽然不是最优的，但该序列具有较好的自相关特性．

则天线1在前2个周期T内发射的信号为：

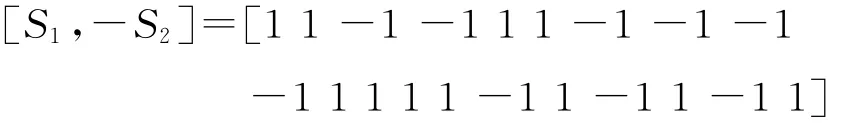
根据空时编码的构造原理，则另一个发射天线的二相码为

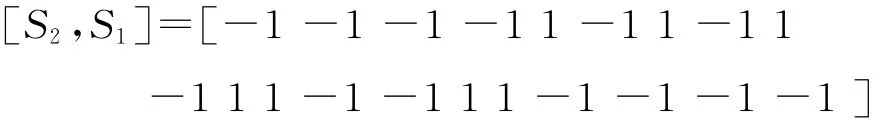
下面采用冲击脉冲类型的超宽带信号对二相码进行调制．随着固态电子和光电子器件的不断发展，可以产生高功率的UWB信号，在理论上仍然以一阶高斯型脉冲波形的对发射信号进行模拟，幅度由混沌二相码Ci控制式：

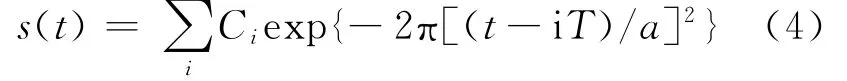
式中：a为脉冲形成因子（决定超宽带脉冲波形）；T为子码宽度，即单个脉冲的持续时间．取a＝0．55ns，T＝1ns得到的发射信号波形见图1．

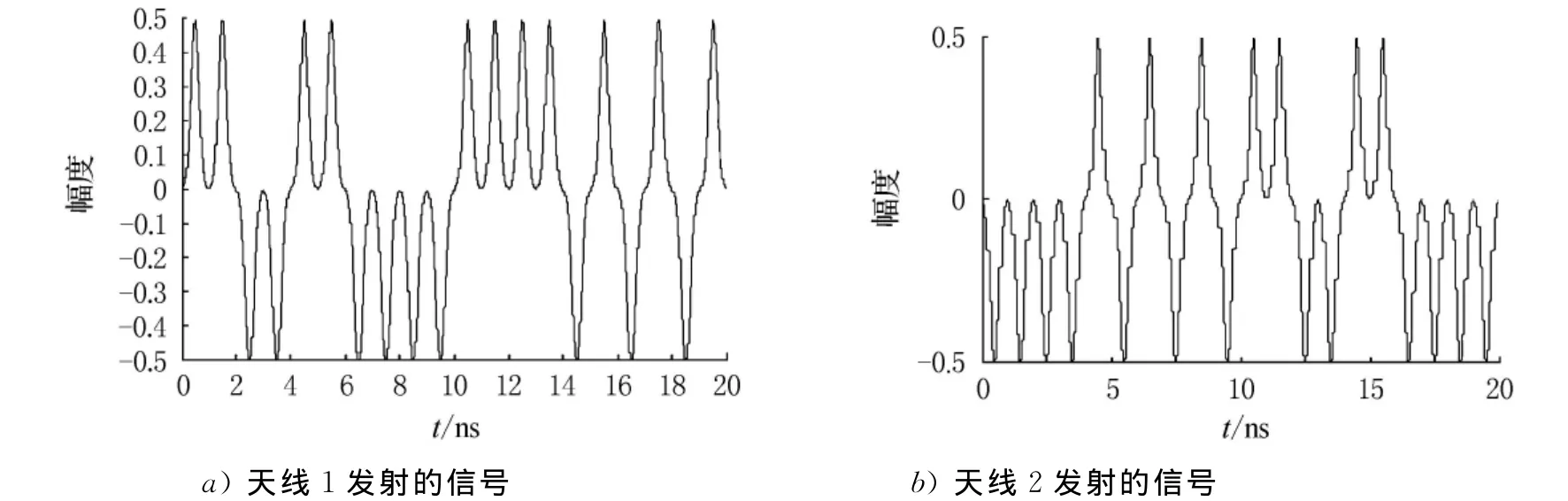
图1 发射信号波形

2 MIMO雷达回波及相关处理

在MIMO通信中接收到的信号为

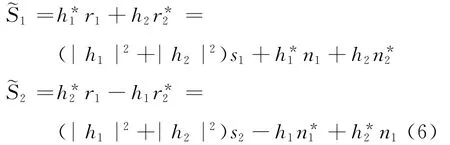
对于通信系统信道模型可以认为是已知的，一般服从瑞利分布，可以采用如下处理并判决，即可将不同的信号进行分离：而对于雷达系统，目标往往是未知的，可以用统计模型进行分析处理．但在进行信号处理时，不再把S1和S22个信号独立分析，而是将天线1，天线2在发射的2个周期内的信号作为整体来处理，接收端仍然可以使用相关处理的方法来进行回波信号的识别．

以某一复杂目标的RCS分布为例，对于超宽带雷达系统而言，一般目标的信道模型为

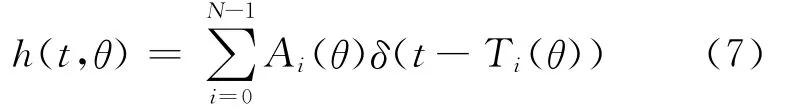
式中：Ai，Ti为散射中心的强度和时延；θ为目标姿态角；N为散射中心数目．

而对于复杂目标或当目标表面涂覆有吸收材料时，此信道模型并不存在．根据瞬时电磁散射理论，可把每个散射中心看作“色散信道”，入射波的幅度随持续时间的增加而衰减，由此物理过程得到的更为理想的超宽带雷达目标信道模型为［10］：

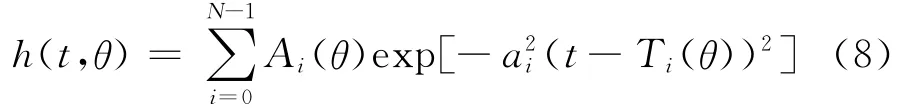
设冲击响应波形为图2a）（天线1正对着目标时）：

则接收到的信号为

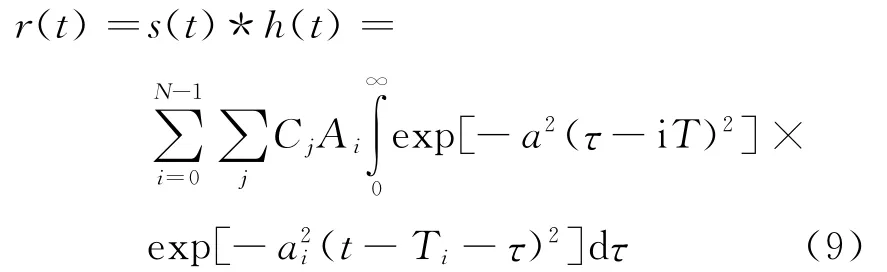
为便于分析问题将接收端设置为两个，在信噪比为20dB的条件下，得到图2b），c）的2个不同接收端的回波信号．天线1，2发射的信号在接收端分别经过相关处理后的回波信号波形，c）是转角发生变化后的回波，尖峰的位置基本不变，只是某些峰的振幅有或大或小的起伏，仍然具有目标的特性．

而对于不同信号，因为具有正交特性，如果进行相关处理，经过脉冲累积后，输出近似为零．

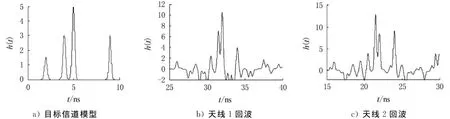
图2 目标信道模型及回波信号

3 目标的检测方法

雷达系统中一般RCS的分布一般是未知的，可使用统计处理方式对目标进行检测．目标采用二进制假设检验，即：H0代表目标不存在，H1代表目标存在．

设M×N系统中的发射矩阵为S，在此假设发射矩阵S为方阵，其秩一般都为M，才能组成M个正交的发射信号，S＋是S的Hermitian变换（又称Moore－Penrose逆）

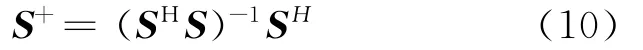
又因为S为正交方阵，故SHS＝ S2I，S2＝（｜s1｜2＋｜s2｜2＋…＋｜sm｜2），在讨论实矩阵时，S－1＝SH／S2＝ST／S2，检测时对接收到的信号进行如下处理：

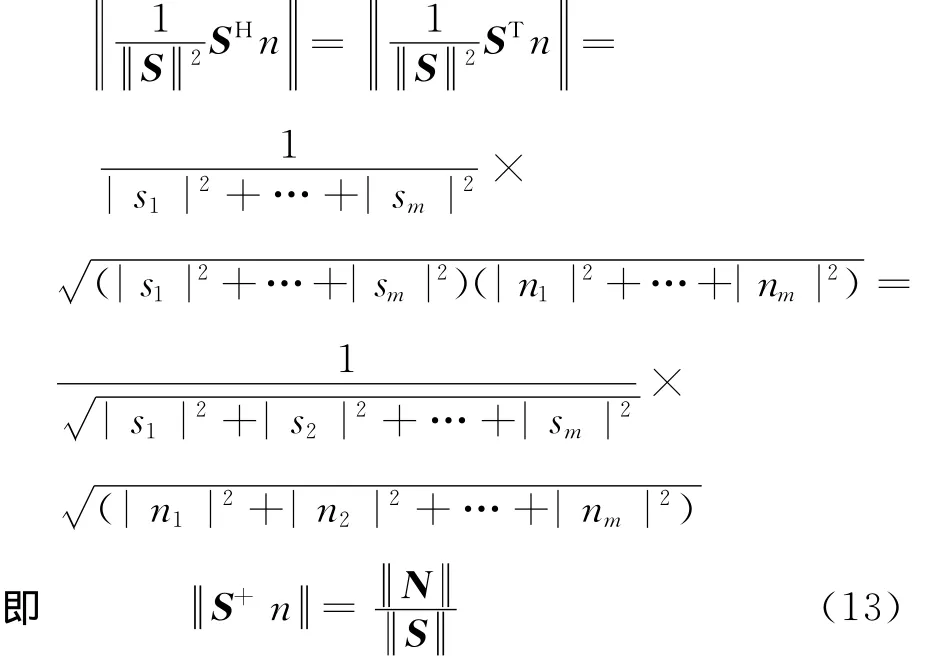
则对接收处理后的信号进行能量检测：

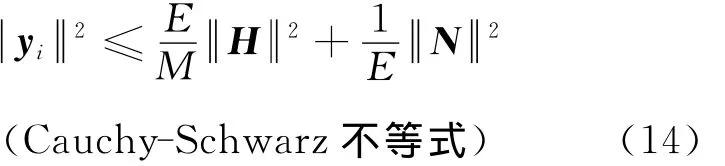
对于N个接收天线，假设目标RCS为Swerling－I型慢起伏时

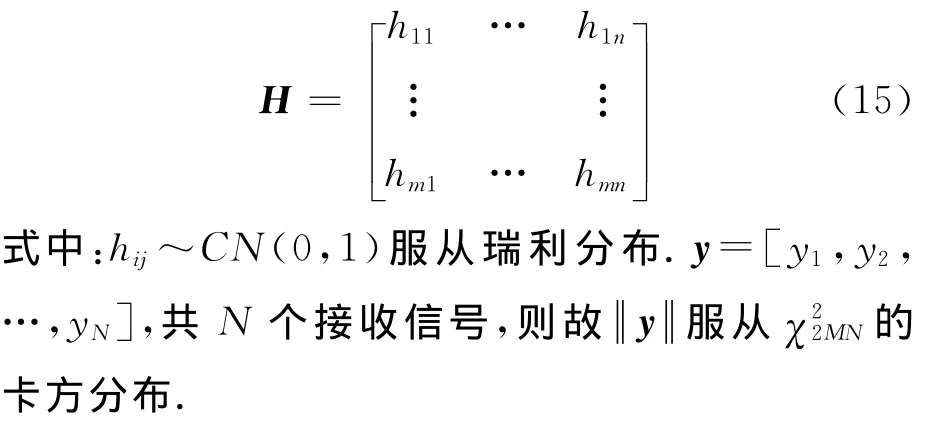
设门限为γ，则最优的奈曼－皮尔逊的检测器如下：

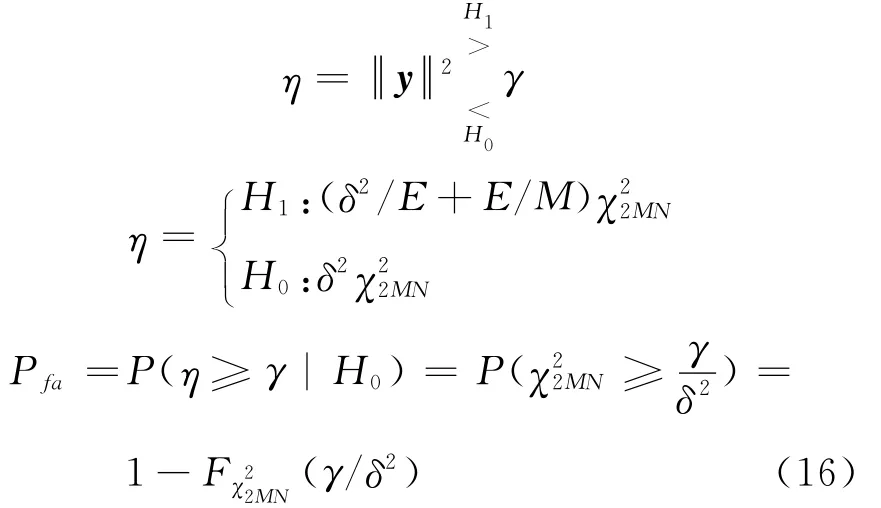
在虚警概率确定后的门限大小为：

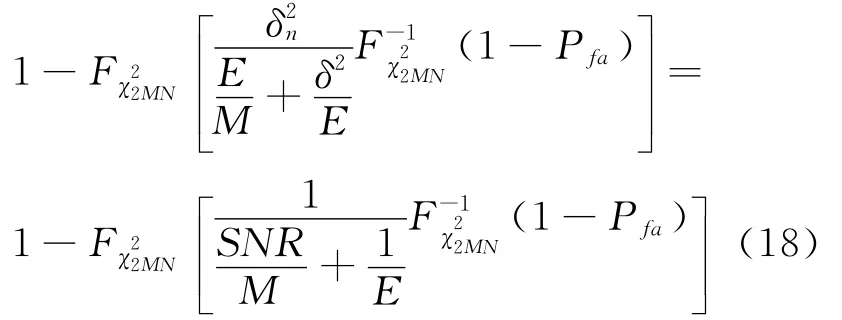
取每个发射波形的能量｜si｜2＝1／M，即E＝1，和最大似然比检测（GLRT）的相比，最优的奈曼－皮尔逊的检测器可以得到相同的结果［12］．而当E＜1时，该检测器的检测性能优于GLRT．而通常超宽带信号的能量都小于1，假设选取发射信号的平均功率为－10dBm，则E＝1／10．图3给出了一般窄带系统和本设计系统在不同发射接收天线的情况下，检测概率随信噪比的变化［13］．由检测概率的仿真曲线可以看出，本系统检测性能得到了很大的提高．

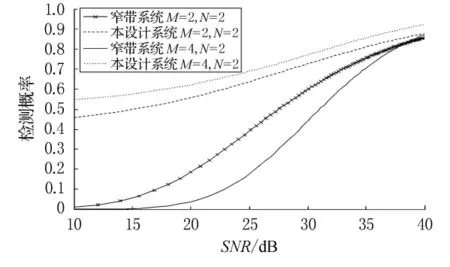
图3 不同发射接收天线数的目标检测概率对比

4 结束语

MIMO雷达是一种新体制雷达，也是下一代雷达发展的主要方向之一，采用空间分集与信号分集技术，要求发射机和接收机都被分开放置，整个雷达系统可从不同方向对目标进行探测，较好地克服了目标RCS的角闪烁所带来的性能损失，获得了较大的空间分集增益，从而在信号检测能力上优于传统雷达．本文使用混沌二相码对超宽带高斯脉冲进行相位调制，根据通信系统中的STBC编码方法，产生了完全正交的发射信号，然后模拟了复杂目标的回波信号，并推导了其检测概率，相对于窄带系统，发现能够较好地进行目标的检测，对实践具有一定的指导意义．

［1］FISHLER E，HAIMOVICH A，BLUM R，et al．MIMO radar：an idea whose time has come［C］／／Philadelphia Pennsylvania USA：Proceeding of the IEEE 2004Radar Conference，2004：71－78．

［2］FISHLER E，HAIMOVICH A，BLUM R，et al．Performance of mimo radar systems：advantages of angular diversity［J］．Conference Record of the Thirty Eight Asilomar Conference on Signals，Systems and Computers，2004（1）：305－309．

［3］BEKKERMAN I，TABRIKIAN J．Target detection and localization using MIMO radars and sonars［J］．IEEE Transactions on Signal Processing，2006，54（10）：3873－3883．

［4］STOICA P，LI Jian，XIE Yao．On probing signal design for MIMO Radar［J］IEEE Transactions on Signal Processing，2007，55（8）：4151－4161．

［5］LEHMANN，HAIMOVICH．High resolution capabilities of MIMO radar［C］／／Asilomar Conference on Signals，Systems and Computers，2006：25－30．

［6］LI J，STOICA P．MIMO radar signal processing［M］．Wiley－IEEE Press，2008．

［7］刘婧逸，张 杰．MIMO雷达正交恒包络OFDM信号设计［J］．武汉理工大学学报，2010，32（3）：110－114．

［8］ALAMOUTI S M．A simple transmit diversity technique for wireless communicaitons［J］．IEEE Journal on Selected Areas in Communications，1998，16（8）：1451－1458．

［9］哈米德·贾法哈尼．空时编码的理论和实践［M］．西安：西安交通大学出版社，2007．

［10］ASHTARI A，THOMAS G．Radar signal design using chaotic signals［C］／／Waveform Diversity and Design Conference IEEE，2007：353－357．

［11］黎海涛，徐继麟．超宽带雷达目标回波建模［J］．系统工程与电子技术，2000，22（10）：41－44．

［12］ANTONIO DE MAIO，LOPS M．Design principles of mimo radar detectors［J］．IEEE Transactions on Aerospace and Electronics Systems，2007，43（3）：886－898．

［13］戴奉周，刘宏伟，吴顺君，等．宽带雷达和窄带雷达在噪声中的检测性能比较［J］．电子与信息学报，2010，32（8）：1837－1842．