振动台试验过程中基于加速度响应的动力特性识别＊

葛继平 王志强 王红伟

（上海应用技术学院城市建设与安全工程学院1） 上海 200235）

（同济大桥桥梁工程系2） 上海 200092） （上海师范大学建工学院3） 上海 201418）

0 引 言

在振动台试验过程中，需要确定各级地震波激励后，试件损伤导致的结构频率变化，从而确定结构的刚度变化情况．这样的方法有：白噪声输入方法和自由振动方法．其中白噪声输入是指根据试件的动力特性输入指定峰值加速度的白噪声；自由振动方法是指对试件施加一指定拉力的水平荷载，然后突然释放或者输入矩形波后突然停止的方式．这2种方法中的峰值加速度大小或拉力大小都是根据既能够达到有效识别结构动力特性，又不会引起试件损伤的原则确定的．M．M．Hachem对桥墩进行了双向荷载作用下的振动台试验时，同时采用了白噪声输入和施加拉力突然释放的自由振动方式［1］．K．J．Elwood对建筑框架在地震激励过程中的重力倒塌进行了研究时，采用施加拉力突然释放的自由振动方法［2］．N．S．Johnson在对大比例尺2跨连续梁桥进行地震响应过程中，采用白噪声输入（白噪声峰值加速度为0．1 g）和输入矩形波后突然停止的自由振动方式［3］．国内的研究者在研究时，大都采用0．05 g白噪声输入的方式进行动力损伤的识别［4］．目前为止，已有的方法都是采用外加激励的方式确定结构的频率，这些为了测量结构频率的激励增加了试验的工作量，而且测量的可靠性也值得商榷．主要原因是在相同的激励方式下，不同损伤程度的同一试件，不一定能够激励起结构的最大损伤状态，具有一定的局限性．

本文根据一组桥墩的振动台试验测试数据，采用时域中的随机子空间方法直接根据该级加速度响应来确定试件的频率，从而判断同级激励导致的结构损伤状态．

1 试验简介

为初步探讨节段拼装桥墩的抗震性能，设计了一个包含5种不同类型混凝土桥墩的试验方案，其中节段拼装桥墩有3种，其余2种分别为普通钢筋混凝土桥墩和无粘结预应力混凝土桥墩．对该方案采用拟静力和振动台试验2种试验方法进行试验研究．这样该方案包括2组共10个试件，其中第一组5个试件为拟静力试件、第二组5个试件为振动台试件．每组试件试验参数相同，为：是否存在预应力钢筋、不同施工方法、预应力筋的布置位置和存在方式、附加耗能装置．柱身的尺寸为240mm×180mm，墩柱高度1 800mm，沿长边（边长240mm）加载，试件的剪跨比为7．5．混凝土立方体强度为43．2MPa，棱柱体抗压强度为41．5MPa，弹性模量为3．03×104MPa．纵筋直径为10mm，屈服强度为340MPa．箍筋直径为6mm，屈服强度为470MPa．墩底箍筋加密区高度为250mm，箍筋间距为50mm，其余位置箍筋间距为80mm．对于节段拼装桥墩，墩底的节段内箍筋间距为50mm，其余墩身箍筋的间距为80mm．耗能钢筋直径为10mm，无粘结区域的长度为500mm，屈服强度为350MPa．预应力钢筋采用Φj12．7的钢绞线，单根预应力筋有效预应力大小为65kN，预应力筋产生的轴压比为11．2%．试件的恒载轴压比为10%．试件的详细尺寸和配筋情况见文献［4］．试件编号和主要特征见表1．图1为振动台试验加载装置全貌．

表1 试件编号和主要特征

图1 振动台试验加载装置全貌

2 试验识别结果

2.1 白噪声输入

本次试验采用白噪声扫描的方法进行结构的初始动力特性测试，测试内容主要是为了了解地震输入加速度幅值逐步增大的结构频率发展情况．每个工况测得振动台台面输入加速度时程和模型结构各加速度测点时程数据，然后利用振动台试验系统自带的数据采集分析系统，获得各测点加速度反应相对于振动台台面输入加速度时程在各离散频率点处的频响函数（为复数形式），接着利用频响函数虚部的图形就可以进行结构自振频率识别，采用半功率法可以估计振型阻尼比．表2列出了各个试件在弹性状态下的动力特性识别结果．

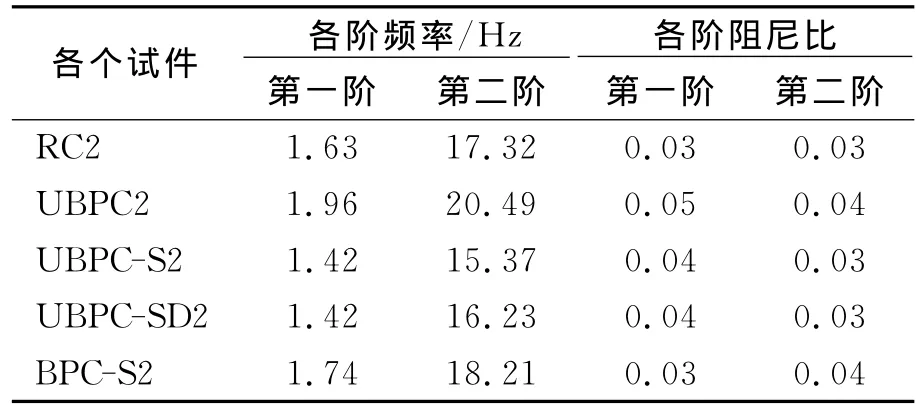
表2 各个试件自振频率和阻尼比试验识别值

2.2 随机子空间识别

对每个地震波的响应采用随机子空间方法进行了动力特性识别［5－8］，得到了结构的第一阶频率和第二阶频率随各级输入的加速度峰值之间的关系，如图2所示．可以看出各个试件随着地震波输入最大峰值加速度的增大，总体上各阶频率处于下降的趋势，说明截面刚度逐渐削弱．

3 简化分析计算结果

对沿墩身高度分布的各加速度通道测点分别进行频率识别，计算各测点的各阶频率及其对应的各阶模态阻尼比．将各阶频率所对应的沿墩身高度分布的频响函数虚部进行归一化处理，即是各阶模态所对应的振型．图3是理想化的期望振形图，图4给出了试验测得的第一阶和第二阶振型．

此外，本文采用3种简化程度不同的模型来计算结构的频率．模型一：仅具有质心平动自由度的理想单自由度模型，忽略质量块的转动质量以及其他因素的影响．模型二：包含质心平动和转动两自由度的模型，考虑质量块的转动质量．模型三：在模型二的基础上考虑桥墩在质量块中的部分为刚臂．3种不同简化程度的模型如图5所示．

对于模型一，频率计算公式如下：

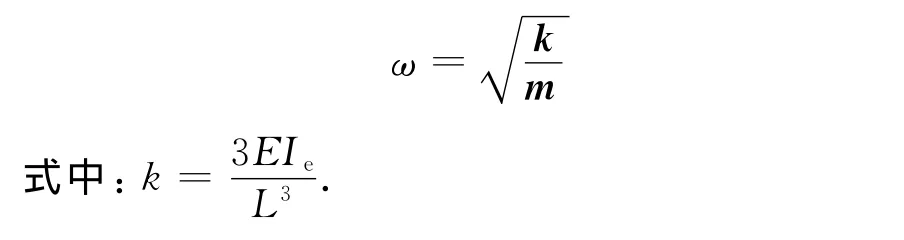
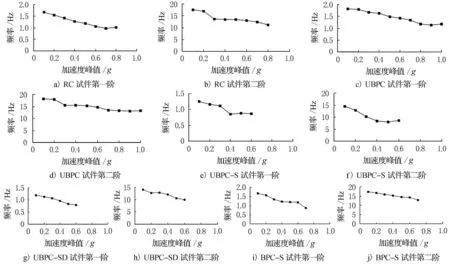
图2 各个试件的频率与加载加速度峰值之间的关系

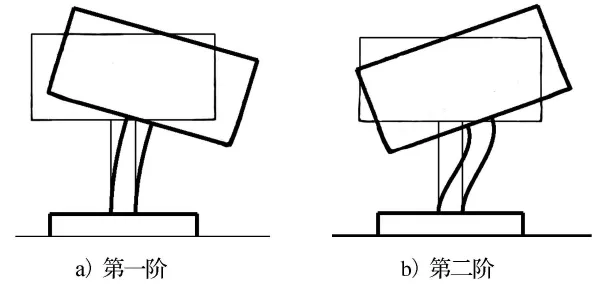
图3 理想化的期望振形图

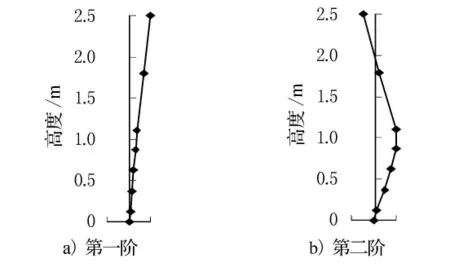
图4 实测振型图

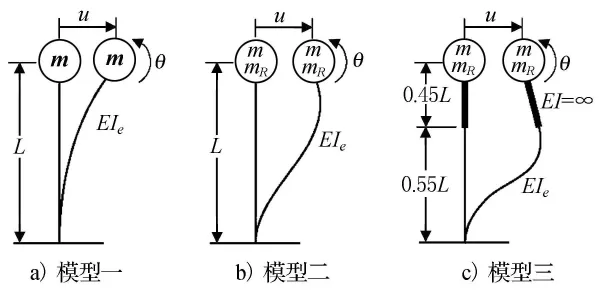
图5 简化程度不同的分析模型

对于模型二，质量矩阵和刚度矩阵如下：

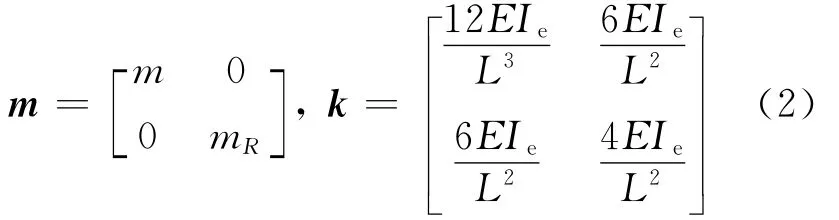
对于模型三，质量矩阵同模型二，刚度矩阵如下：

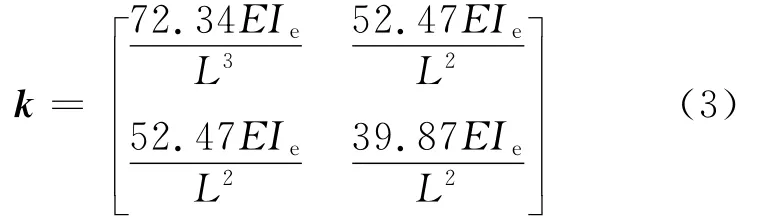
计算得到的结构周期与刚度的变化情况如图6所示，可以看出模型一计算得到的第一阶周期小于模型二和模型三．而且考虑质量块对墩身的刚度的影响后，计算的第二阶周期会变小．与模型二相比，考虑墩嵌固于质量块中部分的钢臂效应后，第一阶周期周期大概小10%，第二阶周期大概小66%．

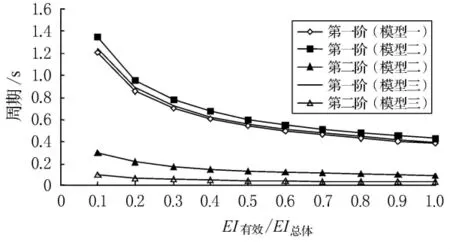
图6 第一阶周期和第二阶周期与有效刚度之间的关系

4 结束语

本文对振动台试验过程中试件动力特性（包括频率，振形，阻尼比）的合理确定方法进行了初步研究，特别是提出了只根据地震响应结果进行试件损伤识别的思路．分析结果表明，仅根据振动台试件响应数据采用时域随机子空间方法进行试件的动力损伤识别是可行的．通过试验过程中测得的频率衰减可以判断桥墩的损伤状态．

［1］HACHEM M M，MAHIN S A，MOEHLE J P．Performance of circular reinforced concrete bridge columns under Bidirectional earthquake loading［R］．Berkeley：Pacific Earthquake Engineering Research Center，University of California，2003．

［2］ELWOOD K J，MOEHLE J P．Shake table tests and analytical studies on the gravity load collapse of reinforced concrete frames［R］．Berkeley：Pacific Earthquake Engineering Research Center，University of California，2003．

［3］JOHNSON N S，SAIIDI M，SANDERS D H．Large－scale experimental and analytical seismic studies of a two－span reinforced concrete bridge system［R］．Nevada：Center for Civil Engineering Earthquake Research Department of Civil and Environmental Engineering，University of Nevada，Reno，2006．

［4］葛继平．节段拼装桥墩抗震性能试验研究与理论分析［D］．上海：同济大学，2008．

［5］沃徳海伦．模态分析理论与试验［M］．北京：北京理工大学出版社，2001．

［6］REN Weixin，GUIDO de Roeck．Structural damage identification using modal data．I：Simulation Verification［J］．Journal of Structural Engineering，2002，128（1）：87－95．

［7］REN Weixin，ZONG Zhouhong．Output－only modal parameter identification of civil engineering structures［J］．Structural Engineering and Mechanics，2004，17（3）：325－332．

［8］De Roeck G，PEETERS B．MACEC2．0－Modal analysis on civil engineering constructions［CP］．Department of Civil Engineering，Catholic University of Leuven，Belgium，1999．