基于振动传递函数的排气系统悬挂点位置优化

廖 芳，高卫民，顾 彦，王 承

（1.同济大学汽车学院，上海201804；2.上海汽车集团股份有限公司技术中心，上海201804；3.百利得安全气囊（上海）公司，上海201315）

排气系统的噪声和振动水平直接影响乘用车的振动噪声性能.随着人们对轿车舒适性要求的不断提高，对汽车噪声和振动控制也提出了更高的要求.在汽车行驶过程中，由于发动机振动和排气激励，导致排气系统产生振动，此振动若传递到车身，将使车身振动加剧并增加车内噪声水平.排气系统悬挂点位置布置直接影响排气系统振动向车身传递，因此，合理布置悬挂点位置是排气系统设计的关键之一.

王继先等［1－3］通过模态分析计算出排气系统的固有频率，并根据模态振型节点确定悬挂点位置；张家玺等［4－7］将平均驱动自由度位移用于汽车排气悬挂点布置，选择平均驱动自由度位移较小点作为悬挂点.本文在已有研究成果的基础上，研究了振动传递函数的基本原理，结合排气系统悬挂点位置布置的实际特点，提出一种基于振动传递函数法的排气系统悬挂点位置布置方法.以某一混合动力轿车（HEV）排气系统悬挂点位置布置为例，结合试验获得的动力总成及悬置系统动力学参数和校核后的排气系统有限元模型，建立动力总成和排气系统的数值模型，计算发动机激励到排气系统的振动传递函数，依据振动传递函数得到排气系统各点在振动频带内的总相对位移响应，由总相对位移响应最小来确定和优化悬挂点位置，并通过实车验证该方法的有效性.基于振动传递函数法的排气系统悬挂点位置布置方法既研究了发动机激励对排气系统悬挂点位置的影响，同时还考虑了每阶模态振型对排气系统振动影响的模态因子，无需大量试算就能快速、准确地得到排气悬挂点位置的优化布置.

1 基于振动传递函数的排气系统悬挂点位置优化的基本原理

忽略阻尼影响，排气系统在激振力作用下，振动微分方程为

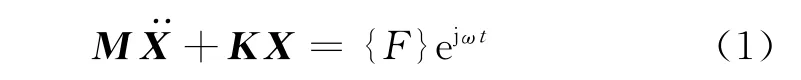
式中：M为排气系统的质量矩阵；X为排气系统的响应位移矩阵；K为排气系统的刚度矩阵；｛F｝ejωt为排气系统受到的激振力；｛F｝为排气系统受到的激振力幅值矩阵；ω为排气系统受到的激振力频率.其各个模态坐标的通解为［8］

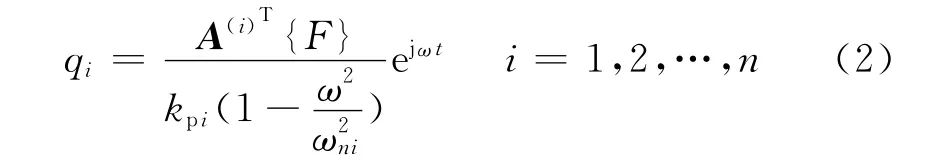
式中：qi为排气系统第i阶模态坐标；A（i）为排气系统第i阶模态向量；kpi为排气系统第i阶模态刚度；ωni为排气系统第i阶模态频率.利用模态振型矩阵作坐标变换后，得到排气系统位移响应的模态表达式为

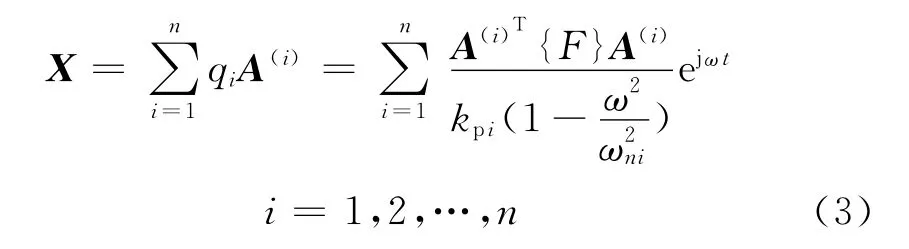
由式（2）和式（3）可知，排气系统的振动位移响应X受激振力的幅值和频率影响，为各阶纯模态运动的线性组合，qi反映了第i阶模态向量A（i）对其贡献量的大小.当排气系统受到来自发动机曲轴的m个不同频率的单位扭矩激励时，其位移响应表达式为

式中：Xu为发动机单位扭矩激励下排气系统的响应位移矩阵；ωk为第k个发动机单位扭矩激励的频率.式（4）为在频率为ωk的发动机单位扭矩载荷作用下排气系统的振动位移响应，定义式（4）为发动机扭矩激励到排气系统各点的振动传递函数，其表征发动机扭矩激励与排气系统各点振动的传递关系，是动力总成和排气组成系统的固有特性，它由系统的结构和参数决定.对动力总成和排气组成的线性系统，若发动机工作在稳态工况，则排气系统各点的位移响应与Xu保持比例关系，即在发动机单位扭矩激励下振动位移Xu越大的点，在稳态激励｛F｝cejωt作用下的振动位移｛F｝c×Xu也越大，其中｛F｝c为发动机稳态扭矩激励的幅值.由式（4）可以推导出发动机在m个不同频率的单位扭矩作用下排气系统各点产生的总相对位移响应XT表达式为

由式（5）可知：

（1）排气系统总相对位移响应XT为各阶主模态A（i）按照一定比例线性叠加，各阶模态对其贡献的大小取决于各阶模态参与因子即模态坐标qi的大小.

（2）当发动机激励幅值为常量时，排气系统各点的振动位移响应正比于XT，总相对位移响应XT越低，发动机激励引起该点的振动越小，该点对车身振动影响就越不显著.传统车辆怠速状态时发动机输出扭矩为等幅值，是一种稳态激励，混合动力车辆驻车充电时发动机处于稳态运转工况，将排气系统悬挂点位置布置在总相对位移响应XT值较小处，能降低排气系统在汽车怠速或驻车充电时的总体振动水平，减少动力总成振动向车身传递.

（3）若动力总成参数和曲轴方向变化，qi和A（i）随之改变，导致总相对位移响应XT变化，对应的悬挂点位置也将改变，因此在基于振动传递函数的排气系统悬挂点位置布置中，发动机激励、动力总成与排气系统的模态参与因子和模态振型共同确定悬挂点位置.

2 基于振动传递函数的悬挂点位置确定及优化

本文以某一混合动力轿车排气系统悬挂点优化为例，对基于振动传递函数法的排气系统悬挂点位置布置方法进行阐述.该混合动力轿车在设计阶段为降低其驻车充电工况的振动水平，需要优化排气系统悬挂点位置.悬挂点位置初始方案根据经验设计，如图1所示.

为优化排气系统悬挂点位置，首先通过试验获得动力总成和悬置系统动力学参数，然后建立排气系统有限元模型并验证该模型的准确性，最后建立动力总成、悬置及排气系统的数值模型，并通过响应分析得到发动机扭矩激励到排气系统各点的振动传递函数，根据振动传递函数计算得到排气系统各点在振动频带内的总相对位移响应.以总相对位移响应最小为依据布置排气系统悬挂点，并获得悬挂点的优化设计方案，最后通过实车试验对排气悬挂点位置布置方案进行验证.

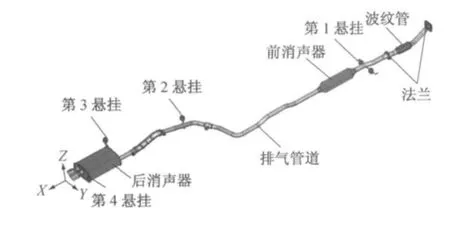
图1 排气系统初始设计Fig.1 Initial design of exhaust system

2.1 动力总成及悬置动力学参数测量

本例混合动力轿车动力总成由传统发动机和电驱动单元EDU（electric drive unit）组成，其中EDU由启动／发电一体电机ISG（integrated starter／generator）、驱动电机以及电机减速器构成.为保证发动机和EDU质心位置、转动惯量以及质量等数据在各个车型平台的互用性并节约样件成本，本文采用三线扭摆法分别测量发动机和EDU的动力学参数，然后通过坐标转换和换算，得到动力总成的质心位置、转动惯量以及质量.在三线摆试验台上，根据能量守恒与刚体转动定律分别对发动机和EDU动力学参数进行测量，运用数据处理软件DPTLAB计算其质量、质心位置及转动惯量.发动机动力学参数测试试验如图2所示，EDU动力学参数测试试验与发动机类似.通过对发动机和EDU质心、转动惯量以及质量的坐标转换和换算，得到动力总成质量为223.3kg；整车坐标系下的质心位置坐标为（－255.9，－15.6，123.1）mm；整车坐标系下的转动惯量Ixx为15.4kg·m2，Iyy为5.7kg·m2，Izz为13.7kg·m2，Ixy为0.7kg·m2，Iyz为－2.8kg· m2，Izx为0.4kg·m2.

悬置刚度试验在动态试验机上进行.各个悬置根据车辆静止状态承受的载荷施加预载.悬置中心通过螺栓固定在试验机上，动作缸对悬置施加10 mm·min－1的速度，并由动作缸上的传感器测得悬置的力和位移，通过力和位移计算出各个悬置的三向刚度.试验测得右悬置X，Y和Z向刚度分别为167，55和176N·mm－1；左悬置X，Y和Z向刚度分别为193，373和396N·mm－1；前、后悬置X，Y和Z向刚度相同，分别为300，50和51N·mm－1.

图2 发动机动力学参数测量Fig.2 Measurement of kinetic parameters of engine

2.2 排气系统有限元模型的建立及验证

该排气系统由法兰、排气管道、波纹管、中消声器和后消声器组成.采用壳单元模拟排气管道、中消声器和后消声器，法兰用六面体单元模拟，通过梁单元来模拟法兰间螺栓连接，用弹簧单元和质量单元表示波纹管.在NASTRAN软件中计算排气系统自由模态.

对排气系统进行模态试验以校核模态仿真分析结果的正确性.在模态试验中，用弹性绳悬吊排气系统，使其处于自由状态.采用软件LMS Testlab数据采集系统记录各点的振动加速度信号，在排气系统管道前端和中端用激振器产生的触发随机信号激励系统，用H1方法估计频响函数.在软件Ploymax中进行模态参数识别.

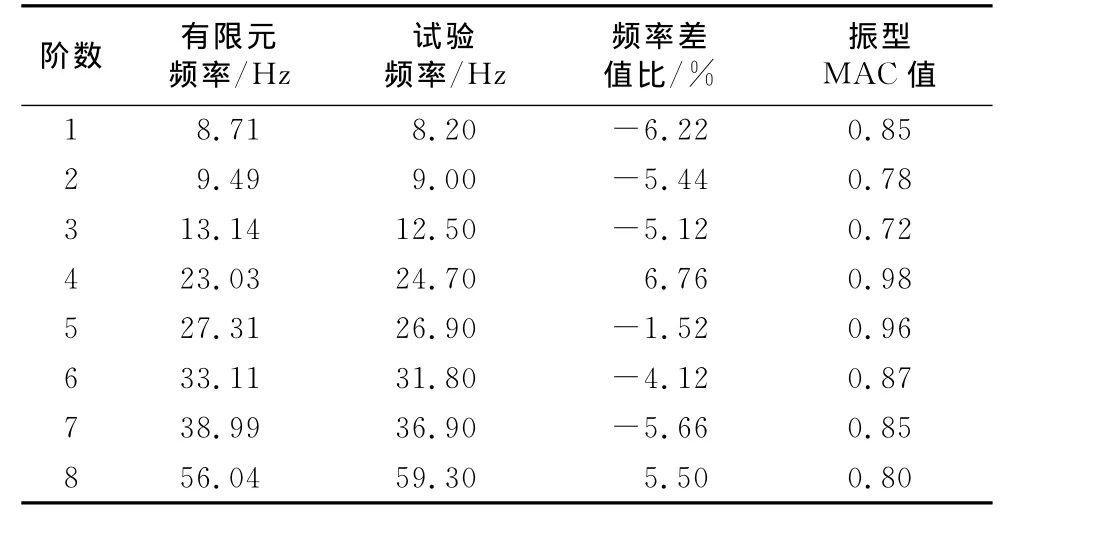
表1 有限元分析和试验测量的排气系统模态比较Tab.1 Modal results comparison between finite element analysis and test

排气系统的前几阶模态对其振动特性影响较大，因此本文对前8阶整体模态进行校核.将有限元计算结果和试验结果导入软件LMS VirtualLab中，对有限元模型进行验证，试验结果和有限元结果的模态频率差值比和模态振型的模态置信准则MAC（Modal Assurance Criterion）值如表1所示，其中MAC值用于检验试验振型和有限元分析振型的一致性［9］.MAC值介于0～1之间，其值越接近1，表明试验振型和有限元分析振型的一致性越好.由表1可知，频率差值比最大为6.76%，MAC值最小为0.72，有限元模型和试验模型吻合较好.此有限元模型能反映排气系统的动力特性.

2.3 基于振动传递函数的排气系统悬挂点位置优化

排气系统有限元模型验证后，输入动力总成和悬置系统的动力学试验参数，建立动力总成、悬置和排气系统有限元模型.模型中悬置用弹簧单元模拟，用质量单元模拟动力总成，在悬置端施加固定约束，动力总成通过排气歧管和排气系统连接.排气系统垂直方向的振动对车身影响最大，因此主要考查排气系统各点的垂向振动，以垂向传递函数的总相对位移响应来布置悬挂点位置.四缸发动机关注的振动频率范围为0～200Hz，在发动机曲轴方向施加0～200Hz单位扭矩，动力总成和排气系统的模态频率截取到400Hz，通过频响分析可计算出排气系统各点的位移响应.在排气系统Z轴正向上表面沿X轴正向依次选取输出点序列，输出点由1开始，增量为1，沿X轴编号，用NASTRAN软件计算得到发动机扭矩激励到输出点序列的传递函数.由于输出点数量较多，图3仅列出排气系统上有限元节点11，21，28，35，43，47和53处的传递函数曲线.由图3中各点振动传递函数可以看出，发动机激励在频率范围0～100Hz内对排气系统振动有显著影响，而在频率范围100～200Hz内对其影响较小.

图3 排气系统部分有限元节点的Z向振动传递函数曲线Fig.3 Curves of vibration transfer function in Z direction of some grids in finite element model of exhaust

根据公式（5），将各个点在频率范围0～200Hz内各输出频率处的响应位移求和，计算出该点的总相对位移响应，各点的总相对位移响应曲线如图4所示.根据在总相对位移响应较小处布置悬挂点原则，结合图4曲线，悬挂点位置潜在的分布点为有限元节点11，21，28，35，43，47和53.

图4 排气系统总相对位移响应曲线Fig.4 Curve of summation of relative displacement response of output grids on exhaust

由于排气系统由2个消声器组成，为了使吊耳受载均匀以提高疲劳寿命，通常采用4个吊耳来连接排气系统和车身，且这4个吊耳分布在两个消声器的前后位置.仅有有限元节点11分布在前消声器前，有限元节点53分布在后消声器后，所以这2个有限元节点必须保留.因为有限元节点21和43所示的整车位置必须布置其他零件，为避免干涉，所以不考虑在其节点处布置吊耳.因而，有3种悬挂点布置方案：方案1为布置在有限元节点11，28，35和53处；方案2为布置在有限元节点11，28，47和53处；方案3为布置在有限元节点11，35，47和53处.为了对3种悬挂点位置布置方案进行取舍，同时考虑批量生产时4个悬挂吊耳具有互换性，并且吊耳和车身受力均匀，本文对3种悬挂点位置布置方案进行重力作用下的车身侧吊耳支反力分析.3种布置方案中车身侧单个吊耳支反力如图5所示.从图5可以看出方案2中车身侧单个吊耳支反力较平衡，因此选择方案2布置悬挂位置，优化后的排气系统悬挂点位置如图6所示，与初始设计方案相比，优化的悬挂位置方案改变了第2悬挂点的位置.

图5 3种方案中车身侧单个吊耳支反力Fig.5 Supporting reaction of hangers in body side of three proposals

图6 排气系统悬挂点位置优化设计Fig.6 Optimization design of hangers location on exhaust system

2.4 优化设计方案的模态频率校核

排气系统与发动机和车身相连，因此排气系统模态频率必须与发动机排气激励频率和车身模态频率分开，避免系统相互耦合产生共振.

在本例混合动力轿车中，发动机为4缸2冲程汽油机，转速范围为1 000～6 000r·min－1.由于驻车充电工况与传统内燃机车辆怠速工况类似，经济转速工况为发动机常用工况，且发动机二阶激励对排气系统的振动影响最大，因此本文主要校核驻车充电和经济转速工况下发动机二阶激励频率与排气系统约束模态频率是否耦合.发动机排气激励频率为f＝pr／60τ，其中，p为气缸数，r为发动机曲轴转速，τ为发动机冲程数.驻车充电转速为1 300r· min－1，对应的排气激励频率为43.33Hz，经济转速为3 000r·min－1，对应的排气激励频率为100.00 Hz.

在本文建立的动力总成和排气系统有限元模型的基础上，以弹簧单元模拟排气系统吊耳，同时在车身侧的吊耳和动力总成悬置端施加固定约束，运用NASTRAN软件计算其约束模态.表2列出了仿真计算得到的排气系统约束模态频率、试验测得的白车身模态频率以及发动机二阶激励频率分布.通过排气系统约束模态频率与白车身频率、发动机排气激励频率的对比，可以判断结构是否存在共振.由表2可知，排气系统频率与白车身频率、驻车充电以及经济转速工况的发动机二阶激励频率相互错开，且频率间隔大于3.00Hz，排气系统优化设计方案较好避免了排气系统与白车身和排气激励的耦合，悬挂点位置优化后的排气系统不会与白车身、驻车充电以及经济转速工况下的发动机二阶激励产生共振.

3 实车验证

本例混合动力轿车在怠速／驻车模式下，混合动力传动系统中没有能量流动，通常情况下发动机和电动机均处于停机状态，此时整车振动水平较低.但当高压电池荷电状态低于限值时，发动机需为动力电池充电，以备下一工况使用.根据本车控制策略，在此驻车充电工况下发动机将以1 300r·min－1的转速通过ISG电机为电池充电，此时车辆振动容易引起乘员警觉，使人产生厌烦情绪，因此本文将驻车充电工况时座椅导轨的振动水平作为本例混合动力轿车振动水平的评价指标之一.以驻车充电工况下悬挂点位置优化设计与初始设计的座椅导轨处加速度和排气系统质心处等效振动加速度的大小，来验证优化方案的优劣，校核基于振动传递函数法的悬挂点位置布置方法的合理性.试验中，在排气系统质心处布置一个三向加速度传感器，如图7所示；座椅处的传感器布置在驾驶员左侧的导轨中央.采集两种悬挂点位置设计下排气系统质心处等效加速度和座椅导轨处加速度.等效加速度越小，在吊耳相同的隔振率下，传递到车身的振动也就越小；座椅导轨处加速度越小，车身的振动也越小.试验测得的振动结果如表3所示.由表3可知，在驻车充电工况下，排气系统优化布置方案中排气系统质心处Z向振动加速度与初始设计相比下降17.58%；优化方案的座椅导轨处X，Y及Z向振动加速度与初始设计相比分别降低了23.56%，21.03%和21.45%，进一步验证随着排气系统等效加速度的降低，整车振动水平也随之降低.试验结果表明利用振动传递函数法布置排气系统悬挂点位置是有效的，可以提高混合动力轿车驻车充电工况的振动性能.

图7 排气系统质心处等效加速度测量Fig.7 Measurement of equivalent acceleration of centroid on exhaust

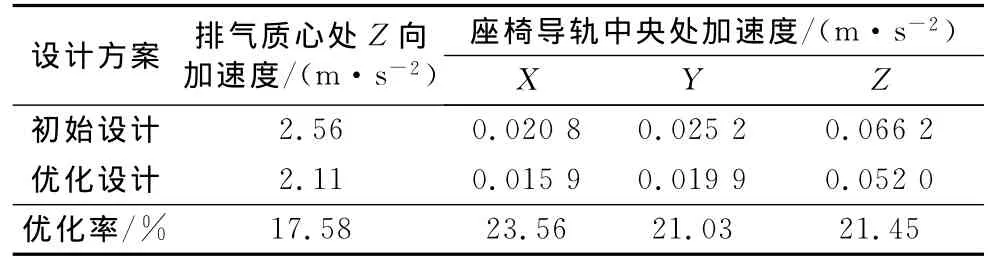
表3 驻车充电工况下两种设计方案振动的比较Tab.3 Comparison between the optimization design and initial one on the vibration accelerations of the HEV in the parking and being charged by engine case

4 结论

振动传递函数的基本原理表明，在混合动力车辆驻车充电工况下，发动机处于稳态工作状态，排气系统各点位移响应正比于总相对位移响应.响应点总相对位移响应越低，发动机传递到该点的振动越小，该点对车身振动的影响就越不明显，因此将悬挂点布置在总相对位移响应较小处，可减少发动机振动向车身的传递.根据该原理提出了排气系统悬挂点位置布置的新方法，并以某混合动力轿车排气系统悬挂点位置布置为例，利用该方法对该轿车排气系统悬挂点布置位置进行了优化，根据总相对位移响应最小原则优化了排气系统第2悬挂点位置.试验结果表明通过该方法布置悬挂点位置可有效减小排气系统振动传递到车身.

在基于振动传递函数原理布置排气系统悬挂点位置的方法中，发动机激励、动力总成与排气系统的模态参与因子和模态振型共同确定悬挂点位置，此方法与传统方法相比无需大量试算就能快速、准确获得排气悬挂点位置，解决了悬挂点位置设计时间长、效率低的问题，该方法设计悬挂点位置是有效的，能运用到排气系统悬挂点位置布置设计中.

［1］ 王继先，李兆文，王务林，等.内燃机排气系统振动特性分析［J］.内燃机工程，2008，29（3）：72.

WANG Jixian，LI Zhaowen，WANG Wulin，et al.Vibration characteristic analysis of engine exhaust system［J］.Chinese Internal Combustion Engine Engineering，2008，29（3）：72.

［2］ 刘名，翁建生.排气系统振动分析和悬挂点位置优化［J］.噪声与振动控制，2010（5）：95.

LIU Ming，WENG Jiansheng.Vibration investigation of exhaust system and optimization of hangers location［J］.Noise and Vibration Control，2010（5）：95.

［3］ 马开柱，陈剑，王建楠.排气系统模态分析及悬挂点位置优化［J］.机械设计及与制造，2008（11）：202.

MA Kaizhu，CHEN Jian，WANG Jiannan.The modal analysis of exhaust system and the optimization of suspender positions［J］.Machinery Design ＆Manufacture，2008（11）：202.

［4］ 张家玺，王远，潘震，等.基于MSC＿Nastran的排气系统悬挂点布置分析［J］.合肥工业大学学报：自然科学版，2009，32（12）：1805.

ZHANG Jiaxi，WANG Yuan，PAN Zhen，et al.Analysis of exhaust system hanger locations layout based on MSC.Nastran［J］.Journal of Hefei University of Technology：Natural Science，2009，32（12）：1805.

［5］ 刘志恩，田静，颜伏伍，等.汽车排气系统悬挂点布置研究［J］.武汉理工大学学报：信息与管理工程版，2010，32（6）：950.

LIU Zhi’en，TIAN Jing，YAN Fuwu，et al.Hanger location layout of automotive exhaust system［J］.Journal of Wuhan University of Technology：Information ＆Management Engineering，2010，32（6）：950.

［6］ 田育耕，刘江华，王岩松，等.汽车排气系统振动模态分析及悬挂点优化［J］.辽宁工程技术大学学报：自然科学版，2009，28（6）：995.

TIAN Yugeng，LIU Jianghua，WANG Yansong，et al.Vibration modal analysis and hanger location optimization of automobile exhaust system［J］.Journal of Liaoning Technical University：Natural Science，2009，28（6）：995.

［7］ 赵海澜，顾彦.汽车排气系统悬挂点优化［J］.计算辅助工程，2006，15（增刊）：230.

ZHAO Hailan，GU Yan.Optimization of vehicle exhaust system hanger location［J］.Computer Aided Engineering，2006，15（suppl）：230.

［8］ 靳晓雄，张立军，江浩.汽车振动分析［M］.上海：同济大学出版社，2002.

JIN Xiaoxiong，ZHANG Lijun，JIANG Hao.Vibration analysis of automobile［M］.Shanghai：Tongji University Press，2002.

［9］ 傅志方，华宏星.模态分析理论与应用［M］.上海：上海交通大学出版社，2000.

FU Zhifang，HUA Hongxing.The theory and application of modal analysis［M］.Shanghai：Shanghai Jiaotong University Press，2000.