超级电容器时变等效电路模型参数辨识与仿真

梁海泉，谢维达，孙家南，赵 洋

（1.同济大学铁道与城市轨道交通研究院，上海201804；2.同济大学交通运输工程学院，上海201804；3.同济大学电子与信息工程学院，上海201804）

在电能存储与回收利用领域，目前已有多种储能器件可供选择，如锂离子电池、飞轮电池和超级电容器等.其中超级电容器具有功率密度大、可大电流快速充放电、使用寿命长和工作温度范围宽等优异特性.这使其在电能存储和回收［1－3］方面具有非常广阔的应用前景.

为在实际应用系统中对超级电容器的动态特性有更深入的了解，并充分发挥其使用性能，需要建立一个准确的等效电路模型.目前国内外文献中有关超级电容器的实际应用系统所涉及到的模型分析多采用经典等效电路模型［4］，该模型是一个线性时不变常系数模型.但是，笔者通过仿真发现，经典等效电路模型不能很好地反映超级电容器的动态特性，而且按照线性时不变常系数模型进行实际系统选型和分析计算的结果往往与真实需求相差较大.

本文在超级电容器等效电路模型的基础上，引入随时间变化的参数来模拟超级电容器工作过程中的动态特性.采用限定记忆最小二乘法对超级电容器的时变参数进行辨识，建立参数随时间变化的函数关系，并利用实验数据在Matlab／Simulink环境下进行仿真.最后，对经典等效电路模型和时变等效电路模型的精度进行了分析和比较.

1 超级电容器模型

超级电容器在工作原理上与传统的静电电容器有很大区别，因此其等效电路模型不能简单的用一个理想电容来代替，需要在深入分析其工作特性的基础上建立能更精确反映其特性的模型.针对超级电容器建模问题，国内外许多研究人员进行了大量的研究工作，目前从不同角度出发建立的模型主要包括电化学特性模型［5－6］、等效电路模型［7］和智能模型［8］等.其中，电化学特性模型从超级电容器的电化学原理出发，建立描述超级电容器容量与电极材料和结构、电解液组成成分等因素之间的数学关系，该模型比较精确地刻画出超级电容器的工作机理，但模型数学表达式非常复杂，而且其计算结果为一个静态电容值，无法反映超级电容器的动态特性，因此不适用于实际应用场合，多用于理论分析计算；等效电路模型采用基本的电路元件（电阻、电容和电感）来模拟超级电容器的工作特性，该模型具有明确的物理意义，可以反映超级电容器工作过程时表现出的动态特性，因而在实际应用中使用最多；智能模型基于人工智能方法建立，该模型将超级电容器看成一个黑箱，建模时不深入分析其内部工作原理，因此模型参数没有直观的物理意义，难以被工程技术人员理解.

综合以上分析，本文选择超级电容器的等效电路模型作为研究对象.目前最常用的等效电路模型是经典等效电路模型，其结构图如图1所示.其中，ESR（equivalent serial resistance）为超级电容器的等效串联内阻，主要表征超级电容器内部发热损耗以及在工作过程中随工作电流大小变化而产生的端电压降；C为超级电容器的等效电容，表征超级电容器的储能特性；EPR（equivalent parallel resistance）为等效并联电阻，用来描述超级电容器的自放电现象，是影响超级电容器长时间储能效果的参数.通常认为自放电现象是指超级电容器在长时间静置时其端电压慢慢下降的现象，而在超级电容器动态工作过程中通常不考虑自放电效应，所以进行超级电容器的动态特性分析时可以略去EPR.

图1 超级电容器经典等效电路模型Fig.1 Classical equivalent circuit model of supercapacitor

超级电容器的经典等效电路模型中的参数为定常参数.文献［9］指出随着充电过程的进行，超级电容器的电容量C会随着端电压的变化而变化，其变化关系基本成线性关系，亦即超级电容器模型的参数值在动态过程中不是一个常数，而应该是一个随时间变化的量.该文献根据此关系以及超级电容器停止充电后其内部电荷发生重新分配的物理现象建立了一个多RC分支的模型，该模型可以在较长时间范围内描述超级电容器的外特性.但该模型每一个RC分支的时间常数的确定存在随意性，必须根据经验和实验数据进行选择，选择不准确则模型精度会受到影响［10］.此外，其模型参数辨识过程采用电路分析方法，即通过欧姆定律和实验数据计算等效电路模型的参数.因为该方法需要在特定的实验条件下进行而不能满足模型在真实工况下在线辨识的要求，所以为满足工程应用中在线监测模型参数的要求，需要采用新的辨识方法来克服以上限制.

综合超级电容器经典等效电路模型和文献［9］提出的时变特性，本文对超级电容器经典等效电路模型进行修改，即将原模型中的定常参数扩展为时变参数，其模型结构图如图2所示.其中，超级电容器端电压U是随时间变化的量，即U＝g（t）；超级电容器等效电容与其端电压之间存在近似线性的函数关系，即C＝f（U）.根据复合函数的原理，可知超级电容器等效电容C与时间t之间存在函数关系C＝W（t），即C是一个时变参数.

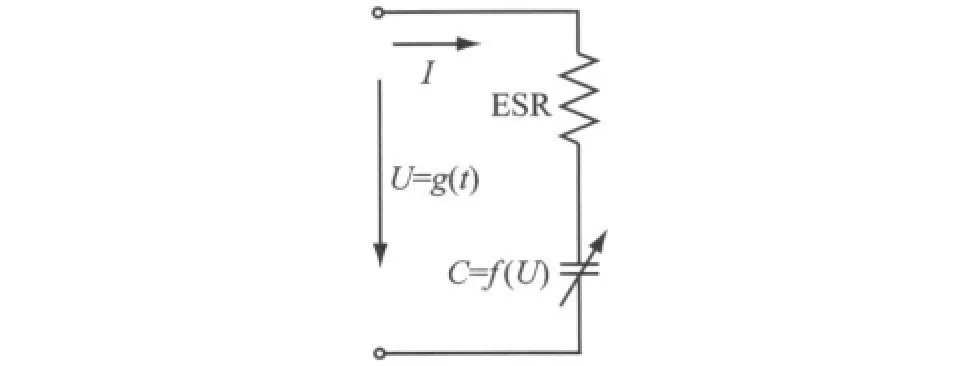
图2 超级电容器时变等效电路模型Fig.2 Time－varying equivalent circuit model of supercapacitor

2 超级电容器时变等效电路模型参数辨识

2.1 时变参数辨识算法选择

针对定常模型的参数辨识问题，通常可以采用递推最小二乘法予以解决.理论上，随着时间的推移，采集到的数据越来越多，递推的最小二乘法应给出更精确的参数估计值.但是递推最小二乘辨识方法在实际应用中，会存在随着辨识数据增多，算法从新数据中获得的信息量下降，算法逐渐失去修正能力，使得参数估计值与真实值发生偏离.这种新数据所提供的信息被淹没在老数据之中的现象，称为“数据饱和”.对于时变系统而言，在辨识过程中必须充分利用新数据所包含的信息，因此数据饱和将导致参数估计值不能跟踪时变参数的变化过程［11］.

针对时变参数的辨识问题，在传统最小二乘法基础上有两种改进方法，即限定记忆法和遗忘因子法.其中，遗忘因子法是在最小二乘法的基础上增加一个遗忘因子作为数据的权重项，随着辨识数据的增加，老数据在遗忘因子的作用下所起的作用越来越小从而降低其在后续参数辨识中所起的作用；限定记忆法通过限制参与参数辨识的数据段来克服数据饱和，即每增加一个新的数据就自动去掉最老的一个数据，保持总的数据段长度不变.通过比较可知，限定记忆法从根本上抑制了辨识数据增多带来的数据饱和现象，从而可以更好地辨识出参数的动态变化过程［12］，因此本文采用限定记忆最小二乘法辨识超级电容器时变等效电路模型的参数.

2.2 限定记忆最小二乘法原理

限定记忆的最小二乘法的基本原理为

2.3 时变等效电路模型参数辨识过程

由图2所示，以电流I作为系统的输入，以超级电容器端电压U作为系统的输出.可以得到整个系统的传递函数如下：

式中：R为等效串联内阻；C为等效电容；U（0）为超级电容器的初始电压；S为拉氏变换算子.需要指出的是，在推导传递函数的过程中，先假设模型参数为常数.在参数辨识的过程中，采用时变辨识算法即可辨识出参数的变化过程.

式中：T为采样周期；n＝1，2，3……；u为阶跃响应.

进一步根据系统的传递函数采用双线性变换可以的到系统的差分方程如下：

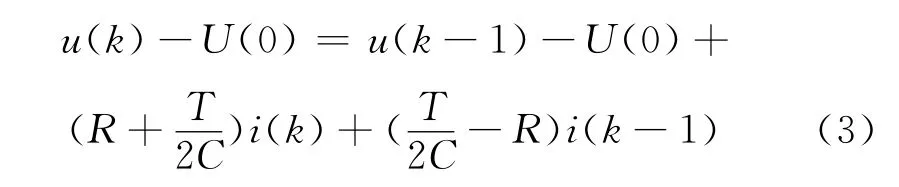
式中：i为流经超级电容器的电流.

由于u（k－1）项的系数为1，因此将其移到等式的左边，得

令

按照式（1）描述的算法并利用实验数据即可估计出θ的值，进一步可求得R与C的估计值.

3 实验与仿真

3.1 超级电容器等效电路模型参数辨识实验

本实验目的为比较超级电容器经典等效电路模型和时变等效电路模型的精度，实验对象为标称电容值为单节80 000F的超级电容器，实验环境温度为20℃，充电电流为30A.在充电过程中应用NI公司的PXI－6133数据采集卡实时采集充电电流和超级电容器端电压数据，采样频率为100Hz.充电过程中的电流和端电压波形如图3所示.

利用该实验数据首先采用普通递推最小二乘法辨识超级电容器经典等效电路模型参数，其具体参数值为：等效串联电阻为0.000 451 53Ω；等效电容为64 342F.

利用相同的实验数据采用限定记忆递推最小二乘法进行辨识.在采用限定记忆最小二乘法时，需要设定记忆长度.为比较不同记忆长度对辨识结果的影响，本文分别取记忆长度为3 000和10 000.辨识结果分别如图4和图5所示.

从以上参数辨识的趋势图可以看出，采用限定记忆最小二乘法可以辨识出时变参数的变化过程.图中清晰地表明超级电容器等效电容的线性变化趋势，同时等效串联内阻在充电过程中基本不变，因此将其当作常数处理是可行的.对比图4，5可以看出，数据长度增加后，电容的带状宽度明显减小，说明随着数据长度的增加，可以减小噪声对参数辨识的干扰作用.

为确定超级电容器等效电容C随端电压U变化的函数关系，采用Matlab自带的曲线拟合工具cftool进行处理.曲线拟合结果如图6所示.

进一步可得到函数关系式为

式中：U为超级电容器端电压，初始值初始端电压为1.121V.

3.2 超级电容器等效电路模型仿真分析

针对超级电容器的经典等效电路模型和时变等效电路模型分别在Matlab／Simulink环境下搭建仿真电路.其中时变等效电路模型的仿真电路如图7所示.图中模块1的功能即反映时变参数C随端电压U的变化关系，其具体的仿真图如图8所示.该模块通过实时测得电容元件两端的端电压然后按公式（8）计算出当前电容值，并根据模块流过的电流改变模块的端电压，作为计算出的理论端电压值.

将实测的充电电流值作为仿真模型的输入，并将经典电路模型参数值和式（8）的曲线拟合结果输入仿真模型，在Matlab／Simulink环境下分别对超级电容器经典等效电路模型和时变等效电路模型进行仿真，得到两种模型的仿真结果及对应的误差曲线分别如图9和图10所示.

由上述仿真结果可以看出，经典等效电路模型虽然能大致描述超级电容器的外特性，但是并不能很好地反映超级电容器的动态特性，其仿真最大绝对误差为42mV，对应相对误差为3.20%；而采用时变等效电路模型的仿真曲线几乎与实测曲线完全重合，仿真电压与实际电压的最大误差不超过12mV，对应相对误差为0.82%.通过比较可知，采用时变等效电路模型可以更精确地描述超级电容器的动态特性，模型整体仿真精度也有极大的提高.

4 结语

本文将超级电容器经典等效电路模型进一步推广为时变模型.采用限定记忆最小二乘法辨识超级电容器模型的时变参数，并利用实验数据在Matlab／Simulink中进行仿真.实验和仿真结果表明，该模型与经典等效电路模型相比能更精确地描述超级电容器在工作过程中的动态过程，从而在超级电容器的实际应用场合可以将更准确的信息反馈给用户，为了解超级电容器的工作状态提供依据.

［1］ 王司博，韦统振，齐智平.超级电容器储能的节能系统研究［J］.中国电机工程学报，2010，30（9）：105.

WANG Sibo，WEI Tongzhen，QI Zhiping.Energy saving system based on supercapacitor［J］.Proceedings of the CSEE，2010，30（9）：105.

［2］ 鲁鸿毅，何奔腾.超级电容器在微型电网中的应用［J］.电力系统自动化，2009，33（2）：87.

LU Hongyi，HE Benteng.Application of the super－capacitor in a MicroGrid［J］.Automation of Electric Power Systems，2009，33（2）：87.

［3］ Abbey C，Joos G.Supercapacitor energy storage for wind energy applications［J］.IEEE Transactions on Industry Applications，2007，43（3）：769.

［4］ Spyker R L，Nelms R M.Classical equivalent circuit parameters for a double－layer capacitor［J］.IEEE Transactions on Aerospace and Electronic Systems，2000，36（3 I）：829.

［5］ Itagaki M，Suzuki S，Shitanda I，et al.Impedance analysis on electric double layer capacitor with transmission line model［J］.Journal of Power Sources，2007，164（1）：415.

［6］ Rafik F，Gualous H，Gallay R，et al.Frequency，thermal and voltage supercapacitor characterization and modeling［J］.Journal of Power Sources，2007，165（2）：928.

［7］ WEI Tongzhen，QI Xinchun，QI Zhiping.An improved ultracapacitor equivalent circuit model for the design of energy storage power systems［C］／／IEEE Conference on Electrical Machine and Systems.Seoul：ICEMS，2007：69－73.

［8］ Farsi H，Gobal F.Artificial neural network simulator for supercapacitor performance prediction［J］.Computational Materials Science，2007，39（3）：678.

［9］ Zubieta L，Bonert R.Characterization of double－layer capacitors for power electronics applications［J］.IEEE Transactions on Industry Applications，2000，36（1）：199.

［10］ Yang W，Carletta J E，Hartley T T，et al.An ultracapacitor model derived using time－dependent current profiles［R］.Knoxville：Institute of Electrical and Electronics Engineers Inc，2008.

［11］ 王志贤.最优状态估计与系统辨识［M］.西安：西北工业大学出版社，2004.

WANG Zhixian.Optimal state estimation and system identification［M］.Xi’an：Northwestern Polytechnical University Press，2004.

［12］ 方崇智，萧德云.过程辨识［M］.北京：清华大学出版社，1988.

FANG Chongzhi，XIAO Deyun.Process identification［M］.Beijing：Tsinghua University Press，1988.