模型再生混凝土单轴受压应力分布特征

李文贵，肖建庄，2，袁俊强

（1.同济大学土木工程学院，上海200092；2.同济大学先进土木工程材料教育部重点实验室，上海200092）

数值仿真方法逐渐用于混凝土材料细微观结构和力学性能方面的研究［1－5］.细观上，再生混凝土是一种由天然骨料、老界面过渡区、老硬化水泥砂浆、新界面过渡区和新硬化水泥砂浆组成的5相复合材料.新老界面过渡区相对于水泥砂浆空隙率较大，含有微裂纹，存在缺陷，是再生混凝土材料中的薄弱区［6－7］.再生混凝土的老界面过渡区处于天然骨料与老硬化砂浆之间，新界面过渡区处于老硬化砂浆和新硬化砂浆之间.由于附着在天然骨料表面的老硬化砂浆存在一些强度退化以及再生粗骨料的机械破碎过程会在老界面过渡区形成细裂纹，因此再生混凝土相比普通混凝土具有一些初始缺陷，界面过渡区和老硬化砂浆是再生混凝土的薄弱部位［8］.

目前，针对再生混凝土单轴受压力学性能已进行了大量的试验研究［9－10］.再生混凝土的受压破坏部位主要集中在新老界面过渡区和老硬化砂浆.以普通混凝土为研究对象，建立二维细观有限元模型，可以分析混凝土在单轴受压情况下的应力分布特征［1，11－12］.本文通过变参数分析讨论了不同天然骨料、老硬化砂浆和界面过渡区的力学参数对再生混凝土应力分布特征的影响.

1 模型再生混凝土

Shah和Winter采用单颗骨料混凝土分析模型，研究在单轴压情况下界面过渡区应力分布特征［13］，Buyukozturk和Nilson提出了9颗骨料混凝土研究模型，并进行了试验和有限元分析［14－15］，Choi和Shah提出了1颗、5颗和13颗骨料的混凝土模型，并采用数字图像相关技术研究其在单轴受压下微裂缝开展信息［16］.本文模型再生混凝土（modeled recycled aggregate concrete）的平面尺寸为150mm ×150mm，天然骨料的直径为28mm，附着在天然骨料周围的老硬化砂浆厚度为5mm.再生骨料之间的间距为9mm，骨料到试件边缘的距离为9mm，新老界面过渡区的厚度均为0.05mm，具体尺寸如图1所示.在模型再生混凝土中，新砂浆、老砂浆和天然骨料3相材料的体积分数分别为54.7%，20.7%和24.6%，该结果与普通再生混凝土中各组分大致相同［17］.

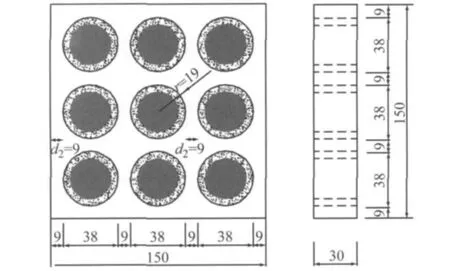
图1 模型再生混凝土示意图（单位：mm）Fig.1 Modeled recycled aggregate concrete（unit：mm）

2 有限元分析

2.1 材料特性

采用有限元软件ABAQUS建立模型再生混凝土的线弹性二维有限元模型，各相材料特性均假定为线弹性，考虑各相材料的弹性模量和泊松比.天然骨料和新老硬化砂浆的弹性模量和泊松比根据各相材料试验数据确定.天然骨料的弹性模量（EA）取70 000MPa，泊松比（νA）取0.16保持不变.老硬化砂浆的弹性模量（EOM）取25 000MPa，泊松比（νOM）为0.22.新硬化水泥砂浆的弹性模量（ENM）取30 000MPa，泊松比（νNM）取0.22，均保持不变.

混凝土材料中，界面过渡区的厚度大约为50 μm［18］，弹性模量大约为砂浆的30%～50%［19］，取界面过渡区的强度为硬化砂浆强度的50%.Rasheeduzzafar和Khan认为再生混凝土中新界面过渡区强度一般大于老界面过渡区强度［7］.再生混凝土老界面过渡区的弹性模量（EOITZ）取13 000 MPa，泊松比（νOITZ）为0.20.新界面过渡区的弹性模量（ENITZ）取15 000MPa，泊松比（νNITZ）为0.20，Ramesh和Sotelino等认为界面过渡区泊松比与硬化砂浆泊松比接近，处于0.02～0.26之间［20］.各相材料的力学参数设定如表1所示.

2.2 有限元模型

选用CPS4R单元（4节点减缩积分平面应力单元），采用扫掠网格划分方法进行单元划分，最后划分得到18 148个规则的四边形单元［21］.模型再生混凝土划分单元后的有限元模型如图2所示.根据变化材料力学参数的需要，共建立7个数值仿真试件.

表1 各相材料力学参数设定Tab.1 Mechanical properties of each phase materials

有限元模型顶部X，Y位移和XY向转动保持自由；约束模型底部Y位移的自由度，保持X和XY方向自由.在模型顶部沿Y方向施加轴向向下的均布荷载30.0N·mm－2.选择静力分析，设置一个荷载步，关闭大变形开关，采用自动搜索，直至计算完毕.模型再生混凝土中各相材料特性均为线弹性，通过单向受压加载讨论应力分布特征，根据应力分布集中现象发现模型再生混凝土的薄弱部位，进而探讨再生混凝土在单轴受压下微裂缝出现和开展的一般规律.

2.3 计算结果

采用ABAQUS的后处理功能，提取模型再生混凝土Y向应力（S22，竖向）、X向应力（S11，水平）、XY向应力（S12，剪切）和Von Mises（等效）应力的应力云图，如图3所示.其中，应力符号的规定为受拉为正，受压为负.

图2 模型再生混凝土有限元模型Fig.2 Finite element model of modeled RAC

在单轴受压荷载作用下，模型再生混凝土的Y向S22在天然骨料处较大，在骨料两侧的界面过渡区位置较小，新界面过渡区最为明显.X向S11在天然骨料处较小，在骨料两侧的新界面过渡区较大，另外骨料之间的新砂浆处也较大.XY向S12在骨料周围角度大概为45°对应的界面过渡区位置较大，其中新界面过渡区位置最为明显.等效应力值Von Mises在天然骨料位置较大，骨料两侧的界面过渡区较小，其中新界面过渡区最为明显.

模型再生混凝土的X向（U1）和Y向（U2）位移分布情况如图4所示.根据模型中各单元的位移分布云图，可以得知各相材料的变形情况.模型再生混凝土X向变形满足Y轴对称分布，试件各相材料的变形不均匀，在界面过渡区和老砂浆处变形出现不连续现象.Y向变形满足Y轴对称分布，试件中天然骨料的变形最小，界面过渡区的变形最大，从底部到顶部Y向变形分布不连续.

在同济大学混凝土材料试验室制作的模型再生混凝土试件见图5.采用Instron 5592刚性试验机对模型再生混凝土试件进行单轴受压试验研究，如图6所示.在单轴加载过程中拍摄试件表面图片后，通过数字图像相关处理技术——细观力学变形测试（optical fringe pattern analysis）［22］处理后得到试件表面的X，Y向位移灰度图，结果见图7.通过比较分析，有限元数值仿真计算结果与试验测试结果基本吻合，说明本文建立的有限元模型是有效和可靠的.

3 变参数分析

模型再生混凝土在单轴受压情况下，改变其组成材料中的天然骨料、新老界面过渡区和老硬化砂浆的材料特性，讨论应力分布特征变化情况.为了比较不同计算参数下模型再生混凝土单轴受压应力分布特征，在试件中选取特定位置提取各单元节点的应力值，绘制应力值与相应位置的分布曲线.所选取的位置分别为试件横截面（Section A—A）、老界面过渡区（OITZ－B）和新界面过渡区（NITZ－C），具体如图8所示.

图8 横截面和新老界面过渡区位置Fig.8 The location of cross section and ITZs

本文通过变参数分析，讨论模型再生混凝土在单轴受压下相关截面和新老界面过渡区应力S22、S11和S12的分布情况和应力集中现象.界面过渡区实际上是一种非线性梯度材料且材料特性随着混凝土使用时间发生改变.本文把界面过渡区简化成匀质弹性材料，代表实际界面过渡区平均力学性能.对不同各相材料力学参数下模型再生混凝土的弹性应力分布规律进行分析，进一步精细化探讨再生混凝土内部应力集中和各相材料相容性特征，为再生混凝土破坏机理和改性措施研究提供定性的理论依据.

3.1 天然骨料

天然骨料的弹性模量分别取30 000，50 000和70 000MPa，其余各相材料的力学参数保持不变.提取模型再生混凝土横截面A—A的Y向应力S22值和X向应力S11值（表2），绘制不同天然骨料弹性模量下的变化曲线图.由图9a可知，随着天然骨料弹性模量增大，界面过渡区承受的竖向荷载减少，天然骨料承受的竖向荷载增加.天然骨料弹性模量取为30 000MPa时，新砂浆承担较大的竖向荷载.

由图9b可知，天然骨料两侧界面过渡区部位出现拉应力集中现象，随着天然骨料弹性模量增大，集中现象愈加突出.S11幅值最大值出现在新老砂浆之间的新界面过渡区部位，随着天然骨料弹性模量增大，应力集中位置基本保持不变.再生混凝土是一种抗拉强度较低的多相复合材料，界面过渡区处受拉应力集中将会导致界面过度处的微裂缝不断扩展而发生破坏.

由图9c～9d可知，老界面过渡区S11满足Y轴对称分布，0～π／2范围内幅值最大值出现在π／5左右.S12满足原点对称，0～π／2之间应力幅值出现在π／7左右.随着天然骨料弹性模量增大，老界面过渡区S11和S12应力幅值位置和分布规律基本保持不变.

表2 不同天然骨料弹性模量下界面过渡区应力分布特征Tab.2 Stress distribution for ITZs with different elastic modulus of natural aggregate MPa

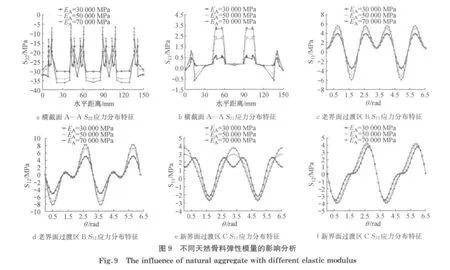
由图9e～9f可知，新界面过渡区S11满足Y轴对称分布，幅值出现在再生骨料两侧，随着天然骨料弹性模量增大，S11幅值位置和分布规律发生变化.S12满足原点对称，0～π／2弧度范围内幅值最大值出现在π／6左右，不随天然骨料弹性模量改变发生变化.S12分布规律随着天然骨料弹性模量增大而发生变化.

3.2 界面过渡区

老界面过渡区弹性模量分别取13 000，19 000和25 000MPa，新界面过渡区弹性模量依次分别取15 000，23 000和30 000MPa，其余各相材料的力学参数保持不变.由图10a可知，随着界面过渡区弹性模量增大，界面过渡区承受的竖向荷载增大，天然骨料S22应力值基本保持不变，仍承受较大的竖向荷载.

由图10b可知，天然骨料两侧界面过渡区处出现拉应力集中现象，S11应力幅值最大值出现在新界面过渡区处.随着界面过渡区弹性模量增大，新界面过渡区S11应力变化不大，应力集中现象仍然很突出.

由表3可知，新界面过渡区和老界面过渡区的S11和S12应力幅值随界面过渡区弹性模量增大而降低，界面过渡区处的应力集中现象也逐渐减弱.老界面过渡区S11和S12应力幅值均大于新界面过渡区S11和S12应力幅值，老界面过渡区的应力集中现象较新界面过渡区更为明显.由于界面过渡区占模型混凝土的体积分数很小，界面过渡区弹性模量的变化对模型再生混凝土弹性模量影响不大.

由图10c～10d可知，老界面过渡区S11满足Y轴对称分布，0～π／2弧度范围内幅值最大值出现在π／5左右.S12满足原点对称，0～π／2弧度之间的幅值出现在π／7左右.随着界面过渡区弹性模量增大，S11和S12应力幅值位置和分布规律基本保持不变.

表3 不同界面过渡区弹性模量下界面过渡区应力分布特征Tab.3 Stress distribution characteristic for ITZs with different elastic modulus of ITZs MPa

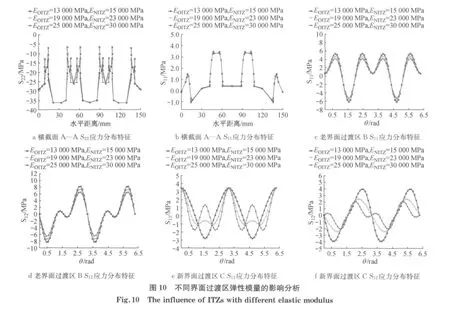
由图10e～10f可知，新界面过渡区S11满足原点对称分布，应力幅值出现在再生骨料两侧，随着界面过渡区弹性模量增大，S11应力幅值位置发生变化，分布规律也发生一定变化.新界面过渡区S12满足原点对称，随着界面过渡区弹性模量增大，S12应力幅值位置和分布规律均发生变化.

3.3 老硬化砂浆

老硬化砂浆弹性模量依次分别取为20 000，25 000和30 000MPa，其余各相材料的力学参数保持不变.由表4可知，随老砂浆弹性模量增大，老界面过渡区的S11和S12应力幅值变化不大.随着老砂浆弹性模量增大，新界面过渡区S11幅值最大值减小，S12幅值增大.老界面过渡区S11和S12应力幅值均大于新界面过渡区S11和S12应力幅值，老界面过渡区的应力集中现象更为明显.随着老砂浆弹性模量增大，模型再生混凝土弹性模量有所提高.

由图11a可知，随着老硬化砂浆弹性模量增大，新硬化砂浆承担的竖向荷载减少，老硬化砂浆和天然骨料承担的竖向荷载增加.横截面A—A的S22分布特征基本不变.由图11b可知，天然骨料两侧界面过渡区处出现拉应力集中现象，S11幅值最大值出现在新界面过渡区处.随着老硬化砂浆弹性模量增大，界面过渡区处拉应力集中现象稍有减弱.

由图11c～11d可知，老界面过渡区S11满足Y轴对称分布，0～π／2弧度范围内应力幅值出现在π／5左右.S12满足原点对称，0到π／2之间的应力幅值出现在π／7左右.随着老砂浆弹性模量的增大，老界面过渡区S11和S12应力幅值出现位置和分布规律基本保持不变.由图11e～11f可知，新界面过渡区S11满足原点对称分布，幅值出现在再生骨料两侧，随着界面过渡区弹性模量增大，S11应力幅值位置和分布规律也发生一些变化.新界面过渡区S12应力满足原点对称，随着界面过渡区弹性模量增大，S12应力幅值出现位置和分布规律发生变化.

表4 不同老硬化砂浆弹性模量下界面过渡区应力分布特征Tab.4 Stress distribution characteristic for ITZs with different elastic modulus of old hardened mortar MPa

4 结论

（1）在单轴受压作用下，模型再生混凝土天然骨料之间的新老界面过渡区出现拉应力和剪应力集中现象，将导致试件内部微裂缝的产生和已有细裂缝的扩展.

（2）随着天然骨料弹性模量增大，天然骨料两侧的新老界面过渡区处的拉应力集中和剪应力集中现象愈加突出.

（3）随着界面过渡区弹性模量增大，新老界面过渡区处的拉应力和剪应力现象有减弱趋势.

（4）随着老硬化砂浆弹性模量增大，老界面过渡区应力变化不大，新界面过渡区应力分布集中现象略有增加.

［1］ Agioutantis Z，Chatzopoulou E，Stavroulaki M.A numerical investigation of the effect of the interfacial zone in concrete mixtures under uniaxial compression：the case of the dilute limit［J］.Cement and Concrete Research，2000，30：715.

［2］ 邬翔，李杰.基于细观物理机制的混凝土损伤数值仿真［J］.建筑材料学报，2009，12（3）：259.

WU Xiang，LI Jie.Meso－mechanism－based simulation of concrete damage process［J］.Chinese Journal of Building Materials，2009，12（3）：259.

［3］ 刘光廷，王宗敏.用随机骨料模型数值模拟混凝土材料的断裂［J］.清华大学学报：自然科学版，1996，36（1）：84.

LIU Guangting，WANG Zongmin.Numerical simulation study of fracture of concrete materials using random aggregate model［J］.Chinese Journal of Tsinghua University：Science and Technology，1996，36（1）：84.

［4］ Sun Z H，Garboczi E J，Shah S P.Modeling the elastic properties of concrete composites：experiment，differential effective medium theory，and numerical simulation［J］.Cement ＆Concrete Composites.2007，29：22.

［5］ 唐春安，傅宇方，朱万成.界面性质对颗粒增强复合材料破坏模式影响的数值模拟分析［J］.复合材料学报，1999，16（4）：112.

TANG Chun’an，FU Yufang，ZHU Wancheng.Numerical approach to effect of interface properties on failure modes in particle－filled composite［J］.Chinese Journal of Acta Materiae Compositae Sinica，1999，16（4）：112.

［6］ Poon C S，Shui Z H，Lam L.Effect of microstructure of ITZ on compressive strength of concrete prepared with recycled aggregates［J］.Construction and Building Materials，2004 18：461.

［7］ Rasheeduzzafar，Khan A.Recycled concrete—a source for new aggregate［J］.Cement，Concrete and Aggregates.1984，6（1）：17.

［8］ 肖建庄，刘琼，李文贵，等.再生混凝土细微观结构和破坏机理研究［J］.青岛理工大学学报，2009，30（4）：24.

XIAO Jianzhuang，LIU Qiong，LI Wengui，et al.On the microand meso－structure and failure mechanism of recycled concrete［J］.Chinese Journal of Qingdao Technological University，2009，30（4）：24.

［9］ 肖建庄，李佳彬，孙振平，等.再生混凝土的抗压强度研究［J］.同济大学学报：自然科学版，2004，32（12）：1558.

XIAO Jianzhuang，LI Jiabin，SUN Zhenping，et al.Study on compressive strength of recycled aggregate concrete［J］.Chinese Journal of Tongji University：Natural Science，2004，32（12）：1558.

［10］ Xiao J Z，Li J B，Zhang C.Mechanical properties of recycled aggregate concrete under uniaxial loading［J］.Cement and Concrete Research.2005，35（6）：1187.

［11］ Ramesh G，Sotelino E.D，Chen W.F.Effect of transition zone on elastic stresses in concrete materials［J］.Journal of Materials in Civil Engineering，1998，10（4）：275.

［12］ Hirsch T.Modulus of elasticity of concrete affected by elastic modulus of cement paste matrix and aggregate［J］.ACI Journal，1962，59（3）：427.

［13］ Shah S P，Winter G.Inelastic behavior and fracture of concrete［J］.ACI Journal，1966，63（9）：925.

［14］ Buyukozturk O，Nilson A H，Slate F O.Stress－strain response and fracture of a concrete model in biaxial loading［J］.ACI Journal，1971，68（8）：590.

［15］ Buyukozturk O，Nilson A H，Slate F O.Deformation and fracture of particulate composite［J］.Journal of the Engineering Mechanics Divis，1972，98（3）：581.

［16］ Choi S，Shah S P.Propagation of microcracks in concrete studied with subregion scanning computer vision（SSCV）［J］.ACI Journal，1999，96（2）：255.

［17］ 刘琼，肖建庄，李宏.老砂浆对再生混凝土力学性能影响模拟试验［J］.四川大学学报：工程科学版，2009，41：76.

LIU Qiong，XIAO Jianzhuang，LI Hong.The study of the effect of old mortar on the mechanical properties of recycled concrete［J］.Chinese Journal of Sichuan University：Engineering Science，2009，41：76.

［18］ Maso J C.Interfacial transition zone in concrete［C］／／RILEM Report of Technical Committee 108－ICC Interfaces in Cementitious Composites.London：E ＆FN SPON，1996：47－60.

［19］ Lutz M P，Monteiro P J M，Zimmerman R W.Inhomogeneous interfacial transition zone model for the bulk modulus of mortar［J］.Cement Concrete Research，1997，27（7）：1117.

［20］ Ramesh G，Sotelino E D，Chen W F.Effect of transition zone on elastic moduli of concrete materials［J］.Cement and Concrete Research，1996，26（4）：611.

［21］ 庄茁，由小川，廖剑晖，等.基于ABAQUS的有限元分析和应用［M］.北京：清华大学出版社，2009.

ZHUANG Zhuo，YOU Xiaochuan，LIAO Jianhui，et al..ABAQUS finite element analysis and application［M］.Beijing：Tsinghua University Press，2009.

［22］ Zhang D S，Luo M，Arola D D.Displacement／strain measurements using an optical microscope and digital image correlation［J］.Optical Engineering，2006，45（3）：033605.