基于置换检验的两步基因特征选择算法

王国胤，罗川江

(重庆邮电大学计算智能重庆市重点实验室，重庆 400065)

0 引言

生物科学与计算机科学是目前发展最迅速的两大学科，而作为这两大学科的交叉产物—生物信息学在基因组研究中发挥了重要的作用，基因芯片作为其中一个崭新的研究领域，正日益受到国际研究者的广泛关注。基因芯片为基因功能的研究提供了一种强有力的工具，对疾病分类、病例诊断以及药物研制等具有非常重要的实际意义。由于实验成本很高，基因样本数量常常很少，只有几十或者上百例，而检测的基因数目相对而言很大，往往高达几千甚至几万［1］。因此，很多传统的方法难以处理这种高维小样本数据。一方面，高维基因数据集中存在大量的噪声，这些噪声基因对类别无分辨能力;另一方面，高维基因数据集中存在大量冗余，这些冗余的基因不会给分类带来额外信息。噪声和冗余基因不仅会导致分类器过度学习，而且会导致计算复杂度急剧升高。Li等［2］指出，对于高维小样本基因数据，不到50个特征基因就能够对类别进行完全分辨。因此，对基因数据的处理，实质上就是对具有“高维小样本”特征的海量数据的挖掘过程。在此过程中，基因特征选择就显得尤为重要。基因特征选择去掉大部分噪声和冗余基因，使得分类精度上升，计算复杂度下降;同时，基因特征选择留下小部分具有生物特性的基因，便于医学研究，病例诊断。

目前，基因特征选择方法主要包括2类［3］:过滤法(filter)和缠绕法(wrapper)。过滤法基于基因内在结构信息，设计不同的准则函数，对单个基因的分辨力进行估计，选择权值较大的作为特征基因。该方法不依赖于分类器对基因子集的评价，计算复杂度低，适合大规模的基因数据处理。例如统计学中的T统计量、F统计量、Wilcoxon秩和检验以及Kruskal－Wallis秩和检验广泛用于基因特征选择中。另外类似T统计量的基因显著性分析方法(significance analysis ofmicroarray，SAM)［4］，以及 F 统计量的集成特征选择与分类的方法(prediction analysis formicroarrays，PAM)［5］同样被证实对基因特征选择的有效性。缠绕法将分类器嵌入到特征选择过程中去，以分类器的准确率为依据，选择的基因子集往往具有高分辨力、低冗余度。但该方法计算复杂度高，并不适合大规模的基因数据处理。例如，递归特征排除策略被广泛用于缠绕法中，代表有SVM－RFE［6］(support vectormachine recursive feature elimination)和 RFE－Relief［7］(recursive feature elimination relief)。另外启发式搜索策略同样被用于缠绕法中，如王树林等［8］首先对基因进行初选，然后采用启发式宽度优先搜索策略对基因进行精选。Peng等［9］同时考虑基因“分辨力”和“冗余度”，采用最小冗余最大关联度量基因子集的重要性基因，然后搜索基因的方式选择基因子集。

现有的基因特征选择存在如下需要改进的地方:1)基因选择的数目依赖于先验知识。多数方法结合分类器准确率，采用交叉测试的方法，人为地给定基因数目。然而，针对大规模基因数据，基因选择的数目应该依赖于数据本身，基因选择的方法应该是数据自主式的;2)缺少高效的基因去冗方法。多数基因特征选择方法并没有考虑基因之间的相似性、冗余度。而另一些基因特征选择方法采用缠绕法，搜索基因的方式选择基因子集，复杂度较高，且基因选择数量难以确定。针对以上问题，本文分两步过滤噪声和冗余基因，并结合置换检验的方法，能自主地选择出可解释性高的基因子集，计算复杂度低，适合处理大规模基因数据。

1 相关工作

基因特征选择既要去掉噪声基因，又要去掉冗余基因。针对该问题，Peng等［9］提出了一种最小冗余最大关联基因特征选择算法mRMR(minimal－redundancymaximal－relevance)。用VS表示基因子集S的分辨力，WS表示基因子集S的冗余度，则基因子集S的重要性可用如下表达评价

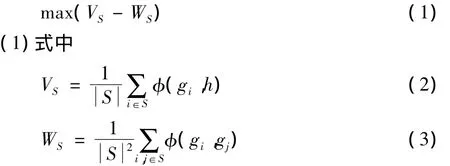
而φ(gi，h)表示基因与类别的关联性，φ(gi，gj)表示基因之间的冗余度。

从mRMR不难发现，一个好的基因子集应该具有最强的分辨力、最小的冗余度。最强的分辨力要求该基因子集能够对所有类别加以分辨识别;最小的冗余度要求该基因子集中基因之间不应具有相同的分辨力。然而，mRMR在选择特征基因的时候需要搜索整个候选基因子集，复杂度高，不适合大规模基因数据处理，后文实验证实了分析结果;并且mRMR同时将“相关性”和“冗余度”融合在一起，并不能有效地去掉冗余基因，后文实验证实了分析结果。针对该问题，本文拆分mRMR中的“相关性”和“冗余度”，采用过滤噪声和冗余基因方法，并结合置换检验，自主的选择基因。

2 两步基因特征选择

2.1 过滤噪声基因

在基因特征选择过程中，只要基因在不同类别不同样本之间存在着显著性差异，那么我们就认为该基因具有分辨能力，应该被选作特征基因。基因在不同类别上的差异可以通过方差分析度量。这种差异性的大小通过F统计量的值来度量

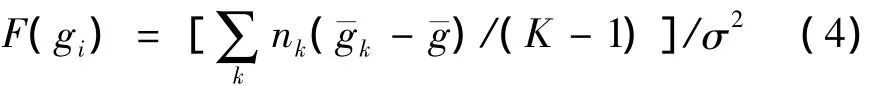
(4)式中:¯g表示样本在基因gi上的均值;¯gk表示类别为k的样本在基因gi上的均值;σ2表示样本在各类别上的合并方差

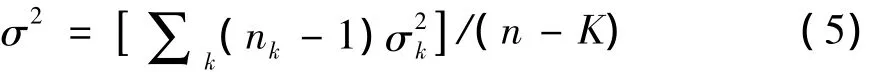
显然F(gi)值越大，基因在不同类别不同样本的差异越大，而在相同类别不同样本的差异越小，则该基因的分辨能力越大，应该排在前面。

2.2 过滤冗余基因

基因特征选择的一个重要目的就是在不降低分类器分辨能力的前提下，选择最少的，最有“鉴别”能力的基因子集。我们采用方差分析中的F统计量对DCOG数据集(数据集来自欧洲生物信息中心，编号为 E－GEOD－13351)基因排序，选择权值最大的100个基因，对基因层次聚类，聚类结果如图1所示。

图1 DCOG数据基因层次聚类结果Fig.1 Hierarchical clustering of DCOG data

2.3 置换检验

邓林等［11］指出方差分析以及线性相关系数需要假设数据服从正态分布，才能够采用假设检验的方法确定基因选择数目;而当数据不服从正态分布时，这些基因选择方法便不能获得最佳实验结果。采用假设检验的方法对结肠癌数据集、白血病数据集和乳腺癌数据集以实验的方式进行了正态性检

从图1中我们可以发现大量具有相同分辨能力的基因聚集在一起，这些基因大部分都是冗余的。对DCOG数据中排在第90位的基因228057_at，该基因对Hyperdiploid类别有分辨能力，但是如果我们只选择最好的89个或者更少的基因，将无法对该类别进行识别。相反如果我们选择最好的90个或者更多的基因，将造成大量冗余基因。一个好的方法是去掉96个冗余的基因，留下4个非冗余的基因。因此，基因特征选择第二步需要检验两个基因是否存在相似性。

Mitra等［10］指出了3种度量基因相似性的方法，包括线性相关系数(correlation coefficient)，最小二乘回归误差(least square regression error)以及最大信息压缩指标(maximal information compression index)。其中线性相关系数广泛用于度量两组随机变量之间的相似性。对于基因gi和gj，他们之间的线性相关系数被定义为验，零假设是样本服从高斯分布，所选取的显著性水平为0.05，实验表明这3种肿瘤数据集都不服从正态分布。

从2.1节中我们知道，对于分辨能力基因，基因在不同类别中存在显著性差异，基因表达值是不可“交换”的;相反，对于噪声基因，基因服从随机分布，基因表达值是可以“交换”的。同理，从2.2节中我们知道，对于存在相关性的两个基因，基因表达值是不可以“交换”的;否则基因表达值是可以“交换”的。基于该思想，我们采用置换检验［12］来确定基因的分辨能力以及基因的相关性。首先给出F和C的显著性和显著性临界值的定义。

定义1 基因显著性。令Fobs和Cobs分别表示原始观察数据的F和C值，Fperm和Cperm分别表示随机置换后的F和C值。经过多次随机置换后(Anderson等［12］指出随机置换次数 no.of perms不应该少于1 000，5 000已经足够)，F和C值的显著性由如下表达式给出

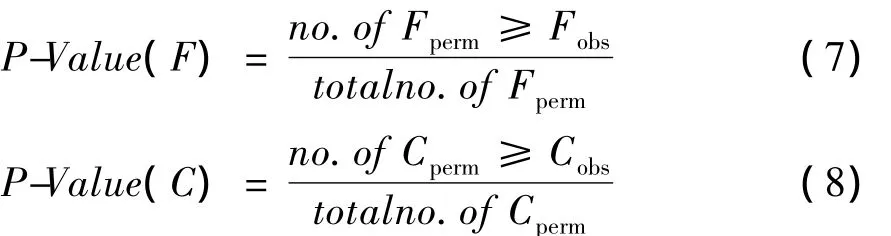
显然，对于噪声基因，随机置换不会改变原始数据分布，Fperm≥Fobs在随机置换中出现频率较高，则P－Value较大;相反，对于分辨能力的基因，随机置换会改变原始数据的分布，Fperm≥Fobs在随机置换过程中出现频率较低，则P－Value较小。根据经典的统计理论，当P－Value小到一定程度，例如1% ，我们拒绝零假设，认为数据不服从随机分布;并接受备择假设，认为基因具有分辨能力，基因之间存在相关性。

定义2 显著性临界值。令Fperms和Cperms分别表示多次随机置换后，统计值F和C从大到小的序列。给定置信度α和β，则F和C的显著性临界值Fcrit和Ccrit由如下表达式给出

2.4 基因特征选择算法

我们提出的基于置换检验的基因选择算法描述如下。本文中，根据实验结果，分别取置信度α=1%和β=0.1%。基于置换检验的两步基因特征选择算法如下。

如图2－图5描述对DCOG数据集作特征选择的过程。算法第1步去掉冗余噪声，图2表示对基因数据做5 000次随机置换，得到关于F的统计分布。此时置信度α=1%，其显著性临界值Fcrit=4.18。当FobsFcrit时，我们接受零假设，认为基因无分辨能力;相反当Fobs≥Fcrit，我们拒绝零假设，认为基因具有分辨能力。如图3所示，从54 675个原始基因中，去掉39 172个噪声基因，留下15 503个有分辨能力的基因。算法第2步去掉冗余基因，图4对基因数据做5 000次随机置换，得到关于C的统计分布。此时置信度β=0.1%，其显著性临界值Ccrit=0.32。当CobsCcrit时，我们接受零假设，认为基因之间不存在相关性;相反当 Cobs≥Ccrit，我们拒绝零假设，认为基因之间存在相关性。如图5所示，从剩余15 503个基因中，去掉15 106个冗余基因，留下379个有分辨能力的基因。

2.5 算法时间复杂度

容易计算算法的时间复杂度，算法第1步中，需要扫描数据集一次，计算每个基因的F统计量的表达值，即时间复杂度为O(nm)。算法第2步中，需要计算基因之间的相关系数C，其时间复杂度是O(n2m)。实际上，算法时间复杂度与剩余的基因数目相关，假设最后选择的基因个数为k，根据实验结果k≪n。则复杂度分别是O(knm)。

3 实验设计与分析

3.1 分类器

本文采用一种简化的PAM(prediction analysis for microarrays)分类器评估基因子集的分辨能力。PAM是Tibshirani等［5］提出的一种集成特征选择与分类方法，能够对多类别问题进行特征选择与分类。本文采用Nikulin等［1］的方法，将PAM分类器简化为

图5 C统计量在DCOG数据上的分布图Fig.5 Frequency distribution of C under DCOG

3.2 实验数据

本文主要采用了 RSCTC'2010 Discovery Challenge［1］12个竞赛数据集，数据集来自欧洲生物信息中心，在 http://tunedit.org/repo/RSCTC/2010/下载。数据集描述如表1所示。

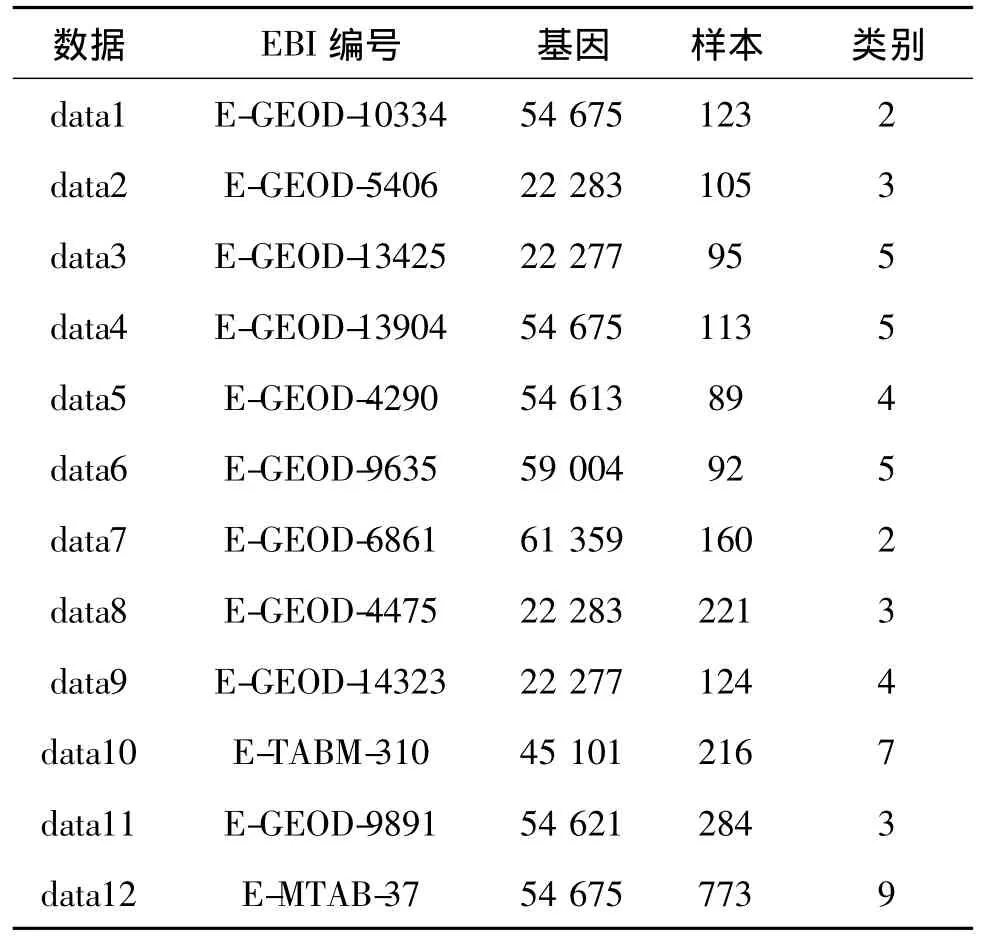
表1 基因数据集Tab.1 Gene datasets

3.3 实验分析

3.3.1 基因相似性分析

为了检验冗余基因对分类结果的影响，我们设计去掉冗余基因与未去掉冗余基因分类器性能对比实验。首先观察算法的3个阶段:1)原始阶段，没有进行特征选择;2)第1步，去掉噪声;3)第2步，去掉噪声和冗余。采用PAM分类器对data1－data12等12个数据集进行LOOCV留一测试。令Crr(S)表示基因子集S的正确识别率;Swfs，Sorn和Srnr分别表示:没有进行特征选择(without feature selection)、去掉噪声(only removed noisy)和去掉噪声和冗余(removed noisy and redundancy)的基因子集。从图6我们不难发现:随着算法处理步骤的增加，基因子集的识别率呈现阶梯上升趋势，即Crr(Swfs)≤Crr(Sorn)≤Crr(Srnr)。原因是算法第1步，我们在加入具有分辨能力基因的同时也加入了大量的冗余基因，这些冗余基因导致分类器过训练、过学习。当加入算法第2步后，冗余基因被去掉，此时基因子集具有最强的分辨能力，最小的冗余度，因此分类器识别率达到最大值。

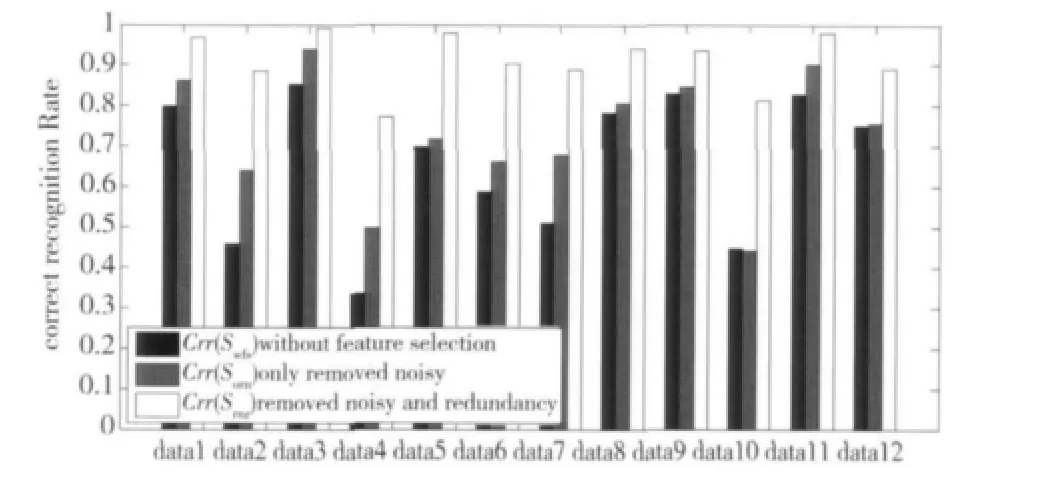
图6 算法不同状态识别率对比Fig.6 Correct recognition rate of different states

不仅如此，试验中我们还记录每次基因选择的数目，如表2所示。令Num(S)表示基因子集S的基因数目，从表2中不难发现，虽然识别率上升了，但是我们选择的基因数目却下降了，即Num(Swfs)≥Num(Sorn)≥Num(Srnr)。Li等［2］认为由于基因数据中样本数目较少，试验中只需要50左右的少量基因，就能完全分辨所有的样本。在本文中，虽然基因数目达到2～5万，但最后留下的50～200基因子集能够很好地识别样本，证明了本算法在选择基因数目上的有效性。

3.2.2 基因识别率分析

Nikulin等［1］采用集成 Wilcoxon秩和检验与Fisher准则函数融合方法ENS(WXN+FDC)对da－ta1－data6等6个基因数据集进行特征选择，并采用PAM分类器进行LOOCV留一测试，得到正确识别率和基因选择数目如表3所示，N表示基因选择数目，P表示正确识别率。Piotr等［13］采用改进的SAM5方法，对data7－data12等6个基因数据集进行特征选择，并采用类似PAM的加权投票分类器WVC－8_v1.4进行LOOCV留一测试，得到正确识别率如表3所示。

表2 算法不同状态基因数目对比Tab.2 Number of gene to select under different states

本文首先采用两步基因特征选择算法对基因进行特征选择，然后采用PAM分类器与LOOCV留一测试法，得到正确识别率和基因选择数目如表3所示。从表3可以看出:1)本文(Ours)和文献［1，13］(Others)在进行特征选择后，分类器正确识别率较原始基因集(Orignal)大大提高，并且留下的基因数目大大减少;2)比较文献［1，13］的结果，本文提出的算法在data1－data12等基因数据上不仅能选择较少的基因子集，而且能获得较高的识别率。其原因是文献［1，13］并没有考虑基因之间的冗余性，造成分类器过学习、过拟合。而本文采用两步基因特征选择算法，不仅去掉了噪声基因，而且去掉了冗余基因。特征选择后剩下的基因子集具有最强的分辨力、最小的冗余度，提高了分类器识别率。

Nikulin［1］和 Piotr［13］没有考虑基因之间的冗余性，Peng［9］考虑基因之间的相似性、冗余度，采用贪心搜索算法，逐步向基因子集中添加基因，添加基因时采用最小冗余最大关联度量基因的重要性。假设已经选择的基因子集用S表示，对基因gi∈{G}－{S}，其权值为

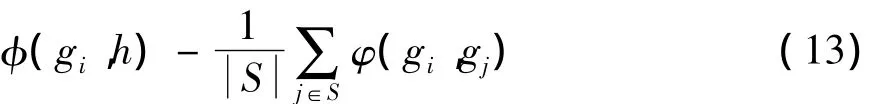
(13)式中:φ(gi，h)表示基因 gi与类别 h的关联性，用 F(gi，h)度量;φ(gi，gj)表示基因 gi，gj的冗余度，用 C(gi，gj)度量。

我们采用mRMR选择最好的200个基因与本文的方法作对比。采用PAM分类器，对选择的基因做LOOCV留一测试，得到正确识别率如表3所示，其中:时间P表示识别率;T表示时间，单位为秒;N表示基因数目。从表3中不难发现，本文提出的算法不仅能选择较少的基因子集，获得较高的识别率，而且计算时间复杂度低，适合大规模的基因特征选择。其原因是mRMR需要搜索整个候选基因集，并且不能很好地去掉冗余基因。例如，对于基因gi和gj，他们具有相同的分辨力，同时他们具有很强的相似性。然而，在式(12)中，gi和gj对基因子集S的冗余度可能较小，原因是基因子集S可能存在大量与gi和gj不相似的基因，这样在冗余度计算的时候，弱化了gi和gj的相似性。

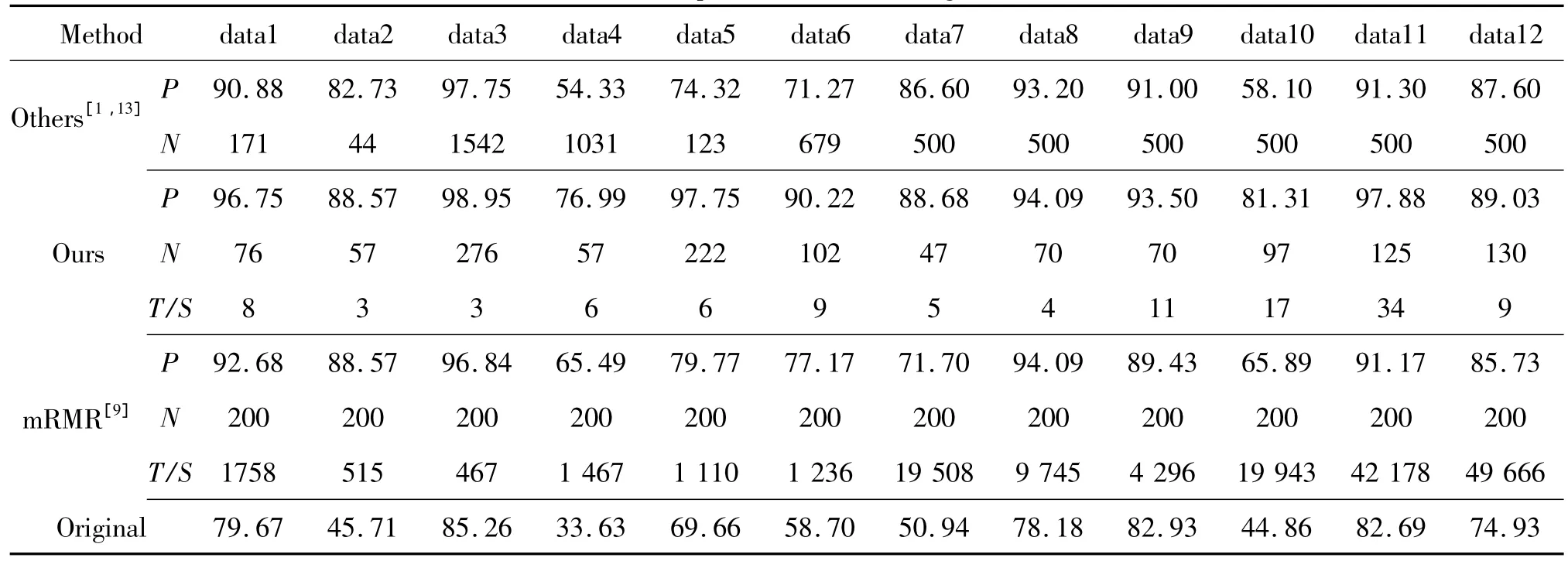
表3 算法正确识别率对比Tab.3 Comparison of different algorithm

4 结束语

高度相关的基因是冗余的，并不会对分类器性能带来提升，因为我们不能从中获取额外有用信息;相反，过多冗余的基因导致分类器过训练、过学习，降低分类器性能。本文提出的基于置换检验的两步基因特征选择算法，不仅能够过滤噪声基因，而且能够过滤冗余基因，结合置换检验，能够高效选择基因子集。

［1］WOJINARSKIM，JANUSZA，NGUYENH S，etal.RSCTC'2010 Discovery Challenge:Mining DNA Microarray Data for Medical Diagnosis and Treatment［C］//Szczuka M，Kryszkiewicz M，Ramanna S，et al.RSCTC 2010.Heidelberg:Springer，2010:4－19.

［2］LIW T，YANG Y N.How many genes are needed for a discriminantmicroarray data analysis［EB/OL］.(2011－06－30)［2011－12－21］.http://wenku.baidu.com/view/885373e9172ded630b1cb692.html.

［3］周昉，呵洁月.生物信息学中基因芯片的特征选择技术综述［J］. 计算机科学，2007，34(12):143－150.

ZHOU Fang，HE Jie－yue.Survey of the Gene Selection Technologies Based on Microarray in Bioinformatics［J］.Computer Science，2007，34(12):143－150.

［4］VTUSHER V G，TIBSHIRANIR，CHU G.Significance analysis of microarrays applied to the ionizing radiation response［J］.Proceedings of the National Academy of Sciences，2001，98(9):5116－5121.

［5］TIBSHIRANIR，HASTIE T，NARASIMHAN B，et al.Diagnosis ofmultiple cancer types by shrunken centroids of gene expression［J］.Proceedings of the National A－cademy of Sciences，2002，99(10):6567–6572.

［6］GUYON I，WESTON J，BARNHILL S，et al.Gene Selection for Cancer Classification using Support Vector Machines［J］.Machine Learning，2002，46(1－3):389－422.

［7］李颖新，李建更，阮晓钢.肿瘤基因表达谱分类特征基因选取问题及分析方法研究［J］.计算机学报，2006，29(2):324－330.

LIYing－xin，LI Jian－gen，RUAN Xiao－gang.Study of Informative Gene Selection for Tissue Classification Based on Tumor Gene Expression Profiles［J］.Chinese Journal of Computers，2006，29(2):324－330.

［8］王树林，王戟，陈火肿，等.肿瘤信息基因启发式宽度优先搜索算法研究［J］.计算机学报，2008，31(4):636－649.

WANG Shu－lin，WANG Ji，CHEN Huo－Zhong，et al.Heuristic Breadth－First Search Algorithm for Informative Gene Selection Based on Gene Expression Profiles［J］.Chinese Journal of Computers，2008，31(4):636－649.

［9］PENG H C，LONG F H，DING C H.Feature selection based onmutual information:criteria ofmax－dependency，min－relevance，andmin－redundancy［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27(8):1226－1238.

［10］MITRA P，MURTHY CA，PAL SK.Unsupervised Feature Selection Using Feature Similarity［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24(3):301－311.

［11］邓林，马尽文，裴健.秩和基因选取方法及其在肿瘤诊断中的应用［J］.科学通报，2004，49(15)，1652－1657.DENG Lin，MA Jin－wen，PEI Jian.Gene Selection Method Based on Rank－Sum test and Its Application in Tumor Diagnosis［J］.Chinese Science Bulletin，2004，49(15)，1652－1657.

［12］ANDERSON M J.Permutation tests for univariate ormultivariate analysis of variance and regression ［J］.Canadian Journal of Fisheries and Aquatic Sciences，2001，58(3):626－639.

［13］PIOTR A.The Extraction Method of DNA Microarray Features Based on Experimental A Statistics［C］//Yao J T，Ramanna S，Wang G Y，et al.RSKT 2011.Heidelberg:Springer，2011:642－648.

(编辑:田海江)