超磁致驱动式流量阀流量特性的数值模拟研究

郭志佳，刘延斌，孟文宝，张 培

(河南科技大学机电工程学院，河南洛阳 471003)

0 引言

随着精密加工、航空航天等技术的发展，人们对精密微进给液压驱动系统的要求也在提高。流量阀作为微进给液压系统的基础件，在响应频率和流量范围方面已不能满足系统的要求。超磁致伸缩材料(giantmagnetostrictivematerial，GMM)具有应变大、响应快和精度高的特点，在流体元件上已有一些应用［1］。图1是精密数字油缸原理图，基于GMA(giantmagnetostrictive actuator)的流量阀是精密数字油缸的控制元件之一。其作为精密数字油缸的核心部件，尤其是数字油缸在需要提供微位移的工进过程中，对流量精确、快速的控制对工件精度会有直接的影响。因此流量阀流量特性的好坏，将直接反应在数字油缸的整体性能上。GMM棒的响应速度小于1μm［2］，因此该阀的响应频率很高，通常能满足系统的要求。本文主要对流量范围进行研究。

图1 精密数字油缸原理图Fig.1 Schematic diagram of the sophisticated digital cylinder

图2是基于 GMA的流量阀结构图，它是由GMA和阀体、阀芯等组件构成。由图2可知，流体由进油口流入阀腔，经过圆锥缝隙流出阀体。阀芯由GMA驱动，在0～60μm里实现位移变化，以改变阀口开度，控制流量。

图2 基于GMA的流量阀结构简图Fig.2 Structure diagram of the giant magnetostrictive－driven flow valve

我们知道，对于流量特性的研究，常用的通用经验公式为Q=K·A·Δpm。其中，K为流量系数，A为阀口流通面积，Δp为压力差，m为节流口形状和结构决定的指数，0.5＜m＜1。流量系数K值并不是常数，与油液密度、节流口结构、形状、压力差等有关系，如果仅凭借经验，很难精确选取。而m值也受多种因素影响，薄壁孔时一般取0.5，细长孔时一般取 1;介于薄壁孔和细长孔之间时，m值就很难选取。由此可见，由经验公式不易得到精确的流量特性公式。而借助Fluent软件进行数值模拟，能够方便有效地建立精确的数学模型。因此本文着力于用Fluent软件分析流量与GMA输出位移和压力差之间的关系，建立精确的数学模型。

1 模型的建立及数值模拟

1.1 建立模型

由图2易知，对流量特性影响大的是圆锥部分的尺寸和缝隙量的大小，而出油口对其影响小。这样可以简化分析，不考虑出油口部分，流体区域可以看作是轴对称的。阀腔主体的三维模型可以看作是在一个阶梯孔，阶梯处是一圆锥面。在小孔轴向垂直的方向上，有一通孔形成出油口。由于主要模拟分析阀腔和圆锥缝隙，忽略出油口部分，因此可以将该三维模型简化为二维模型。

图3是在Gambit软件里进行网格划分和边界条件的定义模型。通过虚线把整个面域分成5个相对规则的部分，分别划分网格，并对圆锥缝隙部分进行局部细化;定义的 Pressure－inlet，Pressure－outlet和Axis分别为进油口、出油口和对称轴;然后导入Fluent软件里，进行数值模拟［4－5］。在 Fluent里以 Space为Axisymmetric的情形分析，取如图3中的在X轴上方对称的一半进行数值模拟［3］。

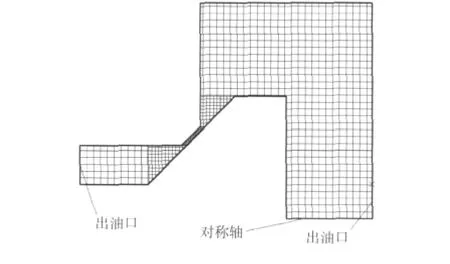
图3 网络划分和边界定义Fig.3 Boundary definition and mesh generation

1.2 仿真方案确定及计算

由于GMA的有效输出位移为60μm，以4μm为一个单位长度，把阀口开度分成15个状态，分别来分析。这样可以了解整个过程的变化趋势，发现其中的规律，有利于掌握该阀的流量特性。

考虑到我们平时使用的液压油大多为46#抗磨压力油，因此为了使仿真的结果与实际更加接近。我们将流体参数设定为46#抗磨压力油的性能参数具体进行如下设置:流体为不可压缩的牛顿流体;流体的密度为ρ=870 kg/m3;动力粘度为μ=0.022 5 Pa·s;流体在流动过程中为单相流;阀芯与阀套的接触边界均设为静止壁面，即选择Wall［6］。这里忽略液温度对压油粘度的影响。

表1给出了进出口流量随GMA输出位移变化的数值模拟数据。表1中左半部分为15个模型进油口和出油口压力的初始加载，然后在Fluent软件Solve菜单里设置Solution Controls对话框参数。选择SIMPLE模型，并有不同模型，设置合适的松弛因子［7］。在Monitors里一方面设置好残差，另一方面设置3个表面监视器，分别监视 Pressure－inlet，Pressure－out和 Pressure－inlet 与 Pressure－out 的 Volume Flow Rate，直至在迭代过程中观察入口、出口以及二者之和的体积流量随迭代次数增加不再变化，即为直线为止。

2 仿真结果及流量特性分析

2.1 数据处理和显示

表1右半部分是15个模型进油口、出油口以及两者之和最终的监视结果(为了便于了解变化趋势，增加64μm，68μm 2个模型)。

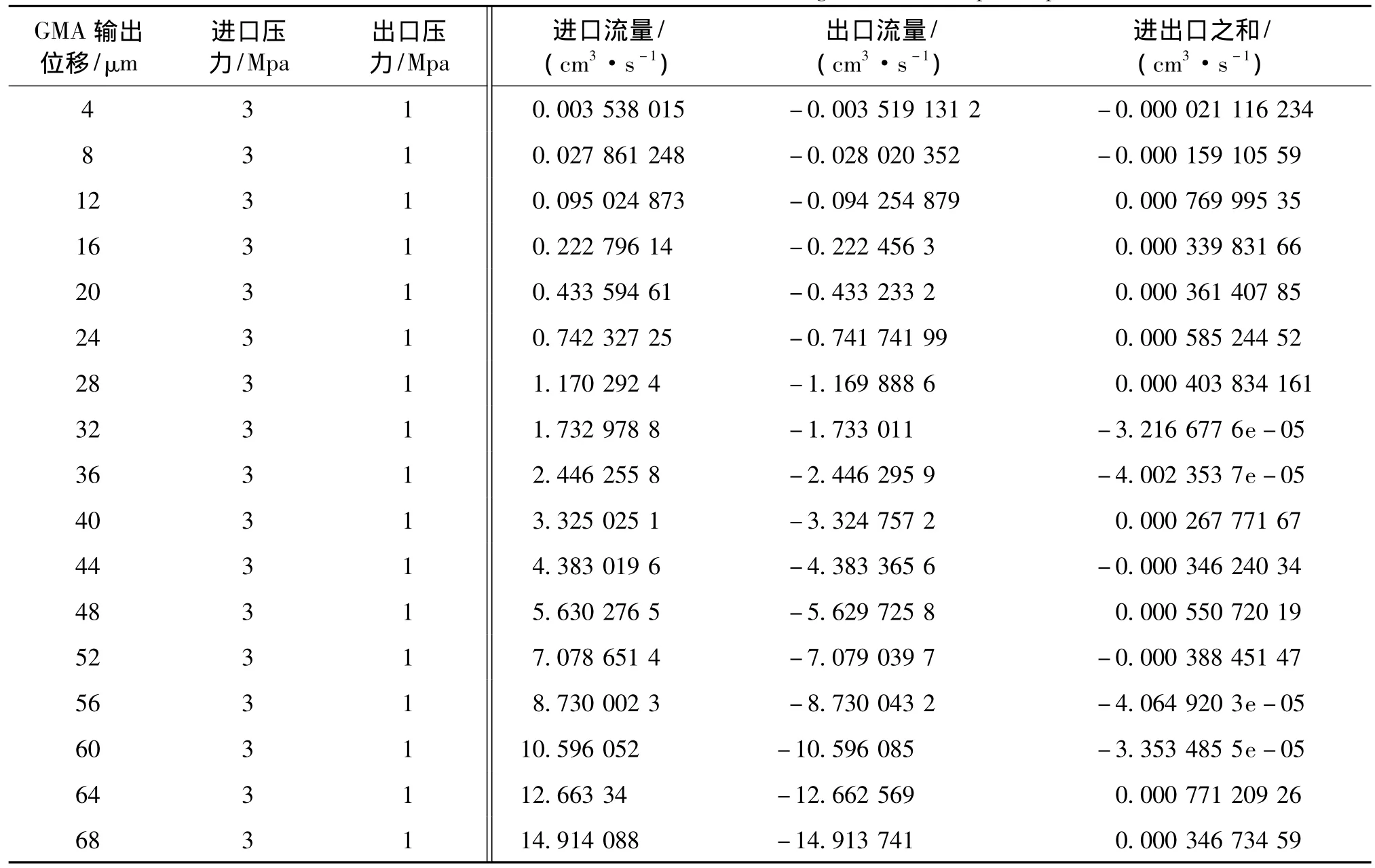
表1 进出口流量随GMA输出位移变化的数值模拟数据Tab.1 Numerical simulation data of the flow of inlet and outlet changeswith the output displacement of the GMA

虽然在监视器中进油口、出油口以及两者之差在直观上已经平衡，为了进一步判断数据计算的可靠性，不妨定义误差率为

(1)式中:in，out和net分别为进油口和出油口的体积流量的绝对值以及两者绝对值之差的绝对值。通过简单计算，很容易得到ε10.6% 。因此，可以断定数值模拟的结果具有可靠性。

Matlab软件具有强大的数据处理能力，为了直观地了解GMA输出位移(注意:阀口开度=输出位移×sin45°，由于两者是线性关系，不影响分析结果，同时方便计算，下文都以此为主)和流量之间的关系，编写程序得到如图4的结果［8］。其中流量y值为(in+out)/2。

图4 位移－流量关系采样图Fig.4 Diagram of the relationship between displacement and flow rate

2.2 流量特性分析

由图4可以看出:

1 )随着GMA输出位移，即阀口开度的增大，流量阀的流量增大。这是由于节流口的面积在增大，在同样的2 Mpa压差的情况下，液压油更容易通过。

2)在GMA整个输出范围内，流量的变化是非线性的。分析原因，在0～68μm范围内，由于阀口开度很小，而圆锥缝隙长度远远大于缝隙量。在这个范围里，这种情况的流动符合缝隙理论。由前言中通用经验公式根据不同节流口结构和形状，可推导出圆锥缝隙流量的经验公式为

(2)式中:K'为圆锥缝隙情况下的流量系数;δ为缝隙量。由此可知，在Δp一定的情况下，q和δ存在非线性关系。

3 数学模型的建立

在2.2节中，只是定性分析了流量－位移的关系，为了验证以上分析的正确性，进一步确定该关系的数学表达式，因此借助Matlab软件，对数据进行三次多项式拟合，并对误差做出简单评定。

由表1可以看出，0～20μm内流量的变化比较大，而20～68μm内相对缓和。不妨先对20～68μm范围内数据进行拟合，对0～20μm内进行细化后再拟合。

3.1 20～60μm段模型建立

图5是通过表1数据，由Matlab软件处理所得的20～60μm段拟合曲线及误差。图5a是拟合所得曲线，图5b是对数值模拟采样值和曲线的误差［8］。

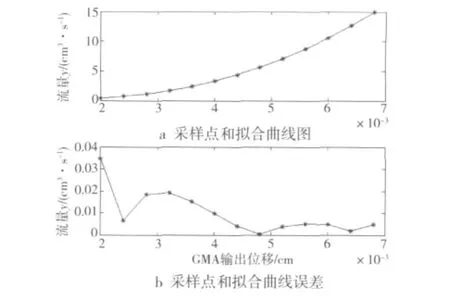
图5 20～68μm段拟合曲线及误差Fig.5 Fitting curve and error in the 20～68μm

计算曲线方程为

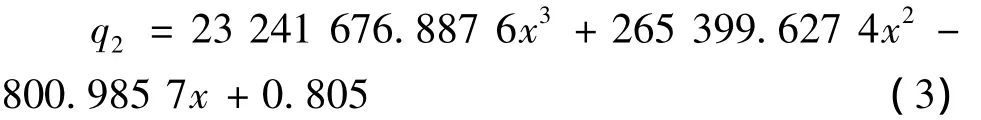
(3)式中:q2是20～68μm段的流量，单位是cm3/s;x是GMA的输出位移，公式中单位取的是cm，和流量单位一致，便于实际分析。

3.2 0～20μm段模型建立

0 ～20 μm段细化后添加的数据如表2所示。

表2 0～20μm段细化后添加的数据Tab.2 Additive data after refinement in the 0～20μm

考虑GMA实际输出位移精度和流量阀的流通能力以及实际油液的过滤精度因素，缝隙小至5μm以下，工件加工精度和油液过滤精度要求过高，难以实际操作，因此在20μm以内，以6μm起，建立数学模型，更有实际意义［9］。

图6是由Matlab程序拟合所得的曲线方程曲线及误差图。其中程序中流量单位为mm3/s，长度单位为mm。计算曲线方程为

(3)式和(4)式是基于GMA的流量阀在进口压力为3 Mpa、出口压力为1 Mpa时的流量特性方程。该方程从一定程度上反应了数值模拟中采样点的变化

3.3 流量阀数学模型

3.1 和3.2 节中只是考虑了在进油口和出油口分别为3 Mpa和1 Mpa时，GMA输出位移和流量的关系。而在2.2节中，虽然经验公式表示q∝Δp，但圆锥缝隙理论并不能完全描述流量阀整个流场的特性。因此，有必要借助Fluent对于不同的进、出油规律。

误差的定义如(5)式，其中i为采样点的值，y是拟合方程在采样点处的值，y(i)是采样点的流量值。由图5和图6可知，拟合误差小于4%，数据可靠。口压力条件下，位移和流量的关系进一步仿真计算加以确定［10］。

图6 6～20μm段拟合曲线及误差Fig.6 Fitting curve and error in the 6～20μm

表3是选取不同采样点，改变进口压力，由Fluent计算整理的数据。

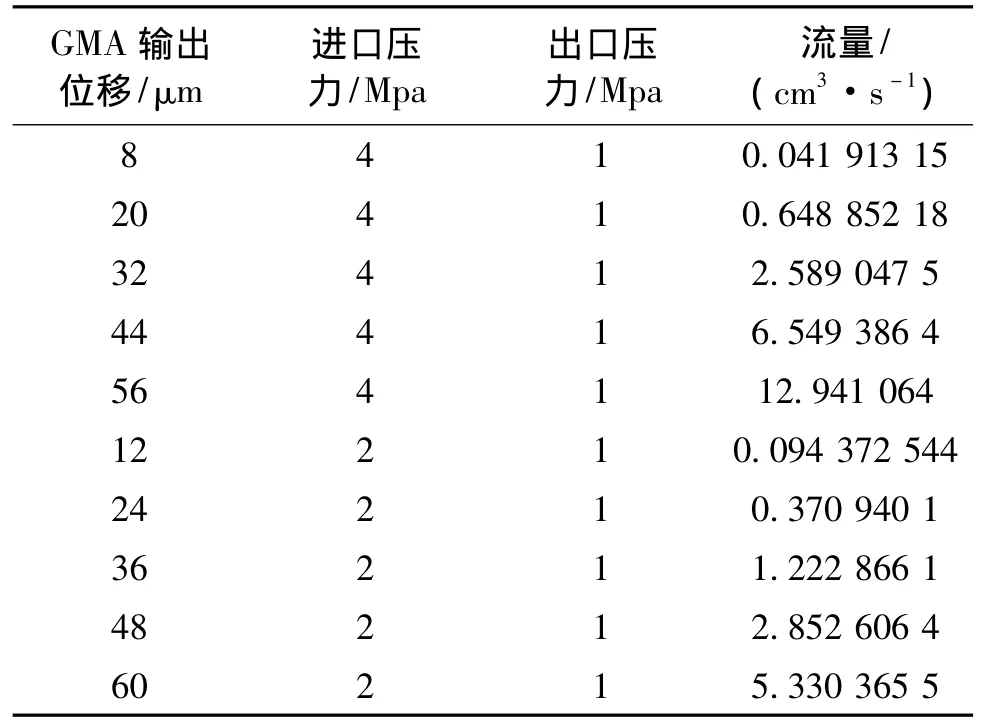
表3 改变不同采样点的进口压力所得流量值Tab.3 Flow values after the changes of the inlet pressure of different sampling points

结合表1，不难看出，当压力差为3 Mpa时，对应采样点的流量近似是2 Mpa时的1.5倍;当压力差为1 Mpa时，与对应采样点比较，约为一半。结合经验公式，因此可以推断:在GMA输出位移一定时，流量与压力差成正比。所以，该流量阀流量特性的数学模型为

(6)式中:上下分别是6～20μm和20～60μm范围里，GMA输出位移、流量和压力差之间的关系;对应流量、位移和压力差的单位分别是cm3/s;cm;Pa;mm3/s;mm;Pa。

4 结语

本文运用Fuent软件对基于GMA的流量阀的流量进行了数值模拟，并分析了采样点变化趋势的原因，通过Matlab软件拟合得到了在进、出口压力为3 Mpa和1 Mpa时的流量特性方程，对拟合误差做了简单的评定;并通过控制GMA输出位移不变，改变进口压力，计算并分析得到流量与GMA输出位移和压力差的数值关系。用此方法，避免了依赖个人经验选择参数的问题，建模过程简单可靠，模型精确。同时，该分析计算结果对该流量阀流量特性的检测和控制有一定的参考意义。

［1］贾振元，郭东明.超磁致伸缩材料微位移执行器原理与应用［M］.北京:科学出版社，2008:287－288，290－291.

JIA Zhen－yuan，GUO Dong－ming.Theory and Aplication of Giant Magnetostrictive Microdisplacement Actuator［M］.Beijing Science Press，2008:287－288，290－291.

［2］陈沛.基于超磁致伸缩致动器的流量控制阀的设计与研究［D］.南昌:南昌工程学院，2011.

CHEN Pei.The design and research of flow valve based on GMA［D］.Nanchang:Nanchang Institute of Technology，2011.

［3］陈帅，吴张永，王小丽，等.一种纯水锥阀流场CFD仿真［J］.流体传动与控制，2009，35(4):29－31.

CHEN Shuai，WU Zhang－yong，WANG Xiao－li，et al.A Water Hydraulic Cone Valve and the CFD Simulation of its Flow［J］.Fluid Power Transmission and Control，2009，35(4):29－31.

［4］李进良，李承曦，胡仁喜，等.精通FLUENT6.3流场分析［M］.北京:化学工业出版社，2009:82－94.

LI Jin－liang，LI Chen－xi，HU Ren－xi，et al.Proficient in FLUENT6.3 Analysis of Flow Field［M］.Beijing:Chemical Industry Press，2009:82－94.

［5］马莹雪，孙得川.电磁阀内部流场数值模拟［J］.机床与液压，2008，36(1):111－113，131.

MA Ying－xue，SUN De－Chun.The Numerical Simulation of the Flow Field in an Electromagnetic Valve［J］.Machine Tool＆ Hydraulics，2008，36(1):111－113，131.

［6］张宏伟.液压滑阀阀芯缝隙流动流场分析［D］.武汉:武汉科技大学，2010.

ZHANG Hong－wei.Analysis ofgap flow field in hydraulic spool valve［D］.Wuhan:Wuhan University of Science and Technology，2010.

［7］闫登强，卿德藩，李岚，等.基于Fluent的不同阀芯与阀体组合的数值模拟研究［J］.机械工程与自动化，2011，164(1):25－26，29.

YAN Deng－qiang，QING De－fan，LILan，et al.Numerical Simulation of Throttle Valves with Different Spool and Valve Body by Fluent［J］.Mechanical Engineering ＆ Automation，2011，164(1):25－26，29.

［8］穆尔.MATLAB实用教程［M］.第2版.高会生，刘童娜，李聪聪，译.北京:电子工业出版社，2010:105－124.

Holly Moore.MATLAB for Engineers［M］.2nd ed.GAO Hui－sheng，LIU Tong－na，LI Chong－chong，translation.Beijing:Publishing House of Electronics Industry，2010:105－124.

［9］席建敏，何忠波，李东伟，等.基于AMEsim的超磁致伸缩高速响应电磁开关阀仿真［J］.机械工程师，2010，234(12):55－58.

XIJian－min，HE Zhong－bo，LIDong－wei，et al.Simulation of the GMV Based on AMEsim［J］.Mechanical Engineer，2010，234(12):55－58.

［10］胡勇，方庆琯.基于力平衡原理的比例阀主阀流量特性研究［J］.流体传动与控制，2011，46(3):18－19.

HU Yong，FANGQing－guan.Flow Properties Research of the Main Valve of Proportional Valve Based on Force E－quilibrium Principle［J］.Fluid Power Transmission ＆Control，2011，46(3):18－19.

(编辑:魏琴芳)