CS-DCSK在Nakagam i-m 衰落信道下的性能分析

陈志贵，徐位凯

(1.厦门海洋职业技术学院，福建厦门 361012;2.厦门大学通信工程系，福建厦门 361005)

0 引言

混沌信号具有宽带、非周期等特性，使得混沌数字调制具有良好的抗多径衰落的性能。为了满足不同的应用需求，研究者们提出了许多不同的混沌数字调制方法［1－4］，其中基于非相干解调的 DCSK(diferential chaos shift keying)由于不需要混沌载波同步，实现简单，受到了最广泛的关注［3－4］。文献［5］表明 FM－DCSK(frequency modulation－DCSK)是一种实现简单的扩频通信替代方案，在保密通信、扩频通信以及超宽带通信中具有良好的应用前景［6－11］。作为一种传输－参考调制机制［12］，一个DCSK符号在前半个周期发送参考信号，后半个周期发送信息承载信号，参考信号与信息承载信号是通过延时电路实现时域正交的。而在宽带应用环境下，目前接收机的宽带射频延时电路还难以实现低成本、低功耗的有效集成。因此，文献［13］提出了一种消除接收机延时电路的DCSK替代方案，该方案采用正交的Walsh码分别调制参考混沌载波和信息承载混沌载波，通过Walsh码实现了参考信号与信息承载信号之间的正交。

尽管在文献［13］中已经给出了 CS－DCSK在AWGN(additive white Gaussian noise)信道和 Rayleigh衰落信道下的性能分析，但在更一般的衰落信道环境下的性能还并不明确，而Nakagami－m模型能够建模无线信道从严重衰落到轻度衰落等不同的传输环境。本文基于Nakagami－m信道模型，基于高斯近似方法，分析了 CS－DCSK在 Nakagami－m 信道下的误码性能，通过计算机仿真验证了分析结果，并比较了信道m参数变化对系统性能的影响以及系统扩频因子与信道多径数之间的关系。

1 系统模型

CS－DCSK借鉴了部分 M－ary DCSK 的思想，同样采用Walsh码作为调制解调实现必不可少的组成部分，区别于多元DCSK的是:在多元DCSK中分别采用M个正交的Walsh码序列对应M个不同的符号，实现了对信号空间的区别;而在CS－DCSK中，仅需要2个正交的Walsh码序列实现二进制的调制，如果把 DCSK 看作传输－参考(transmitted－reference，TR)通信系统［12］，那么在 CS－DCSK 中，2 个 Walsh码序列分别实现对参考信号和信息承载信号的调制。由于2个Walsh码序列是正交的，因此参考信号和信息承载信号也是正交的，理论上与传统的DCSK是一样的，不过传统的DCSK是通过延时电路实现了参考信号和信息承载信号在时域的正交，而CS－DCSK则通过Walsh码序列实现了参考信号和信息承载信号在码域的正交。CS－DCSK发射机原理框图如图1所示，该结构框图与多元DCSK发射机非常类似，同样需要具有N－1个延时单元的延时电路，每个延时单元均延时Tc，但是，理论上它们具有重大的差别，在CS－DCSK发射机中，参考信号与信息承载信号是在相同的时隙上进行传输的，因此，CS－DCSK是二进制调制。特别地，当采用2阶的Walsh码实现CS－DCSK时，其发射机所需的延时电路与传统的DCSK一样，均需1个延时为Tc的延时电路。

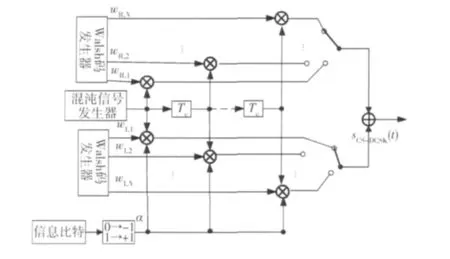
图1 CS－DCSK发射机原理框图Fig.1 Transmitter of CS－DCSK

假定只考虑传输单个符号的情形，则CS－DCSK发射机送出的信号可表示为(1)式中:发送符号a∈{－1，+1}由信息比特b∈{0，1}映射而来;wR，k+1和 wI，k+1分别是用于调制参考信号和信息承载信号的Walsh码序列的码元。

Walsh码是一种正交码，即在同步传输情况下，利用Walsh码作为地址码具有良好的自相关特性和处处为零的互相关特性，且Walsh码生成容易，应用方便。Walsh码可以通过哈达玛(Hadamard)矩阵来产生。假设H是一个2n－1阶的哈达玛矩阵，则2n阶矩阵构造为

在接收端，假定接收机带宽足够大使得接收信号可以无失真的接收，接收端噪声n(t)为0均值、方差为N0/2的加性白高斯噪声，则接收滤波器输出的信号为kTc)+n(t) (6)

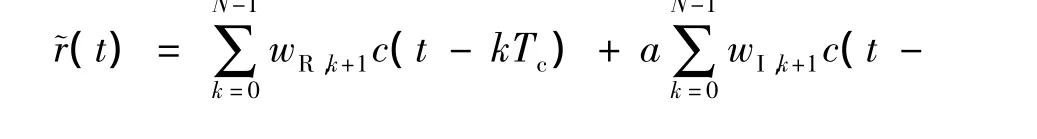
CS－DCSK接收机的原理框图如图2所示，根据系统原理，采用差分相干接收，判决统计量Z表示为

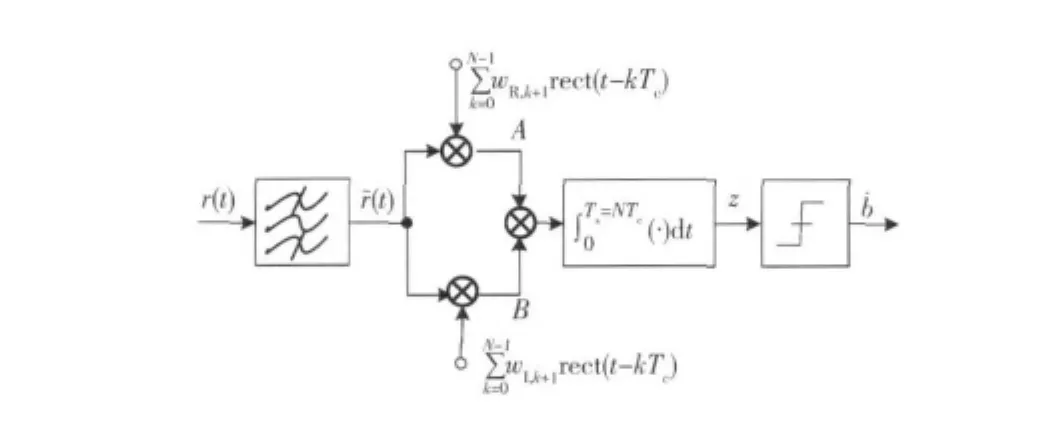
图2 CS－DCSK接收机原理框图Fig.2 Receiver of CS－DCSK

2 误比特率性能分析

基于高斯近似分析方法，CS－DCSK在AWGN信道下的BER计算公式为［13］

因此，CS－DCSK 在 Nakagami－m 多径衰落信道下的BER可对条件BER作期望计算得到，即

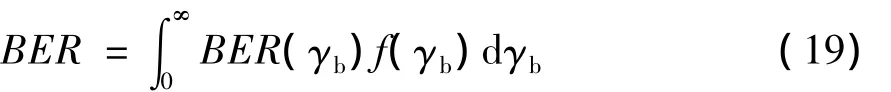
3 仿真结果及分析

仿真中采用Hadamard方法构造Walsh码矩阵，特别地，当W=［+1，+ 1;+1，－1］，矩阵的第1，2行分别用于参考码序列和信息承载码序列，在此情况下，CS－DCSK与传统的DCSK非常类似，在发射端均需要1个延时电路单元，混沌载波由Logistic映射产生。信道为密集多径衰落信道，即信道抽头之间相差一个采样延时，所有的信道增益满足Nakagami－m分布，且每径具有相同的信道参数m，另外，以下仿真结果中，若无特别说明，均为基于二阶Walsh码仿真的结果。

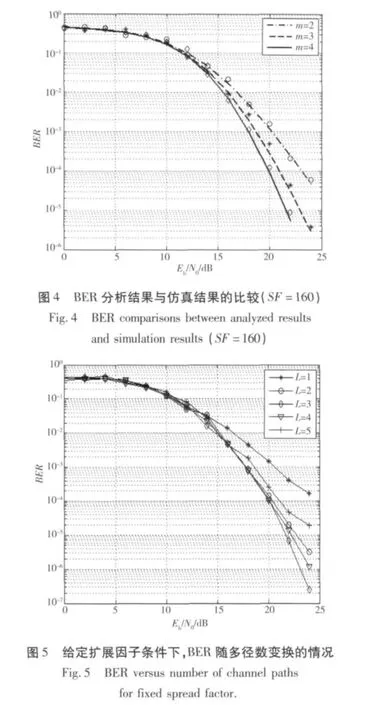
图3和图4给出了扩展因子SF分别为80和160时的BER分析结果与仿真结果对比。图3和图4中实线、虚线和点线分别表示信道参数m=2，3，4时的分析结果，菱形、星形、圆分别为对应的仿真结果。由图3－图4可知，当扩展因子为80时，分析结果与仿真结果有较大的差距，当扩展因子足够大(160)时，仿真结果与分析结果具有很好的一致性。这与AWGN信道下的结果一致，因为高斯近似分析方法只有在扩展因子较大时才具有适应性。另外，从图3－图4可以看出，随着Nakagami－m信道参数m的增加，BER性能逐渐变好，是由于参数m表示了信道的衰落程度，随着m的增加，信道逐渐接近AWGN信道。

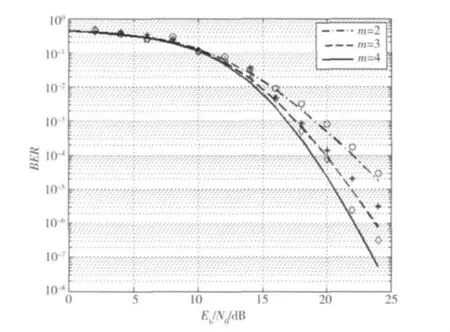
图3 BER分析结果与仿真结果的比较(SF=80)Fig.3 BER comparisons between analyzed results and simulation results(SF=80)

图5给出了扩展因子为80的条件下，随着信道多径数L增加，BER的变化情况，由图5可知，随着L的增加，BER性能逐步变好，当L=3时达到最佳，L再增加时，性能又逐步恶化。这是由于CS－DCSK作为一种扩频技术，具有多径分集的能力，所以当多径数L增加时，BER性能变好。但由于多径会带来符号间的干扰，当给定扩展因子时，L越大，符号间干扰越大，当多径分集带来的增益不足以弥补符号间的干扰导致的性能恶化时，系统的BER变差。

最后，图6给出信道参数m=3的2径信道下，Eb/N0分别为16 dB，20 dB时，BER随扩展因子SF变化的结果，曲线表明:随着SF的增加，BER性能逐步变差。这与AWGN信道下的结果类似，是由于随着SF的增加，接收机相关器引入的噪声也逐步增加，导致系统性能恶化。

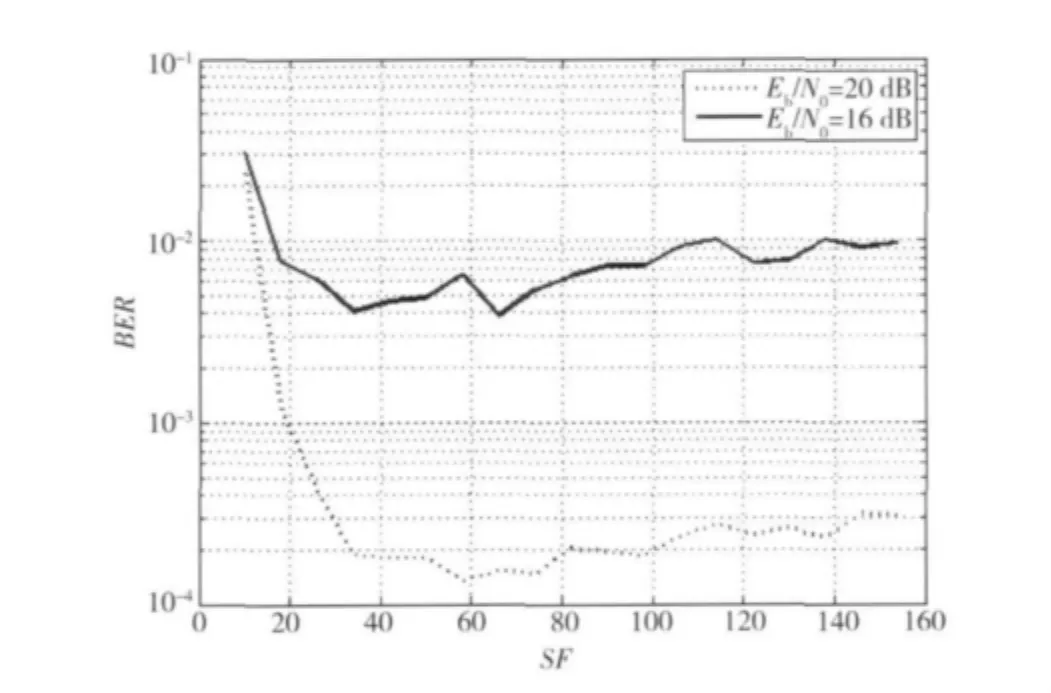
图6 BER随扩展因子(SF)变化的性能Fig.6 BER versus spread factor

4 结语

本文基于高斯近似方法分析了CS－DCSK在Nakagami－m多径衰落信道下的 BER性能，给出了BER的数值积分解，计算机仿真结果与数值结果表明:当扩展因子较大时，分析结果与仿真结果能够很好的吻合，表明该分析方法是可靠的。另外，比较了信道参数m改变时，BER性能的变化情况，分析了信道多径数与扩展因子之间的关系，发现信道多径数与扩展因子之间有最佳的配置关系。

［1］KISG，JAKO Z，KENNEDY M P，et al.Chaotic communications without synchronization［C］//Proceedings of the 6th IEE Conference on Telecommunications，［s.l.］:Conference Publications，1998:49－53.

［2］KOLUNMBAN G，VIZVARIG K，SCHWARZW，et al.Differential chaos shift keying:A robust coding for chaos communication［C］//Proceedings of InternationalWorkshop on Nonlinear Dynamics of Electronic Systems，Seville，Spain:Conference Publications，1996:87－92.

［3］KOLUNMBAN G，KISG，KENNEDY M P，et al.FMDCSK:A new and robust solution to chaos communications［C］//International Symposium on Nonlinear Theory and Its Applications，Hawaii，USA:Conference Publications，1997:117－120.

［4］WANG L，ZHANG C X，CHEN G R.Performance of an SIMO FM－DCSK Communication System ［J］.IEEE Trans.Circuits and Systems－II:Express Briefs，2008，55(5):457－461.

［5］YE L，CHEN G，WANG L.Essence and advantages of FM－DCSK technique versus conventional spread－spectrum communicationmethods［J］.Circuits，Systems and Signal Processing，2005，24(5):657－673.

［6］DMITRIEV A S，KYARGINSKY B Y，PANASA I，etal.Experiments on ultra wideband direct chaotic information transmission inmicrowave band ［J］.Int.J.Bifurcation＆ Chaos，2003，13(6):1495－1507.

［7］SANG－MIN H，POPOV O，DMITRIEV A S.Flexible chaotic UWB communication system with adjustable channel bandwidth in CMOS technology［J］.IEEE Trans.Microwave Theory and Techniques，2008，56(10):2229－2236.

［8］SANG－MIN H，MI－HYUN S，YONG－HWAN K，et al.Low－Rate Chaotic UWB Transceiver System Based on IEEE 802.15.4a［C］//Proceedings of the 3rd European Radar Conference.Manchester，UK:Conference Publications，2006:358－361.

［9］YONG S－K，CHONG C－C，KOLUMBáN G.Non－coherent UWB radio for low－rate WPAN applications a chaotic approach ［J］.International JWireless information Network，2007，14(2):121－130.

［10］MIN X，XUW K，WANG L，et al.Promising Performance of an FM－DCSK UWB System under Indoor Environments［J］.IETCommunications，2010，4(2):125－134.

［11］KOLUMBA G，KREBESZ T，LAU F CM.Feasibility of UWB radio:Impulse radio versus chaos－based approach［C］//Proceedings of IEEE ISCAS，Paris，France:IEEE Press，2010:2450－2453.

［12］RUSHFORTH C K.Transmitted－reference techniques for random or unknown channels［J］.IEEE Trans.Inform.Theory，1964，10(1):39－42.

［13］XUW K，WANG L，KOLUMBáN G.A Novel Differential Chaos Shift Keying Scheme ［J］.International Journal of Bifurcation and Chaos，2011，21(3):799－814.

［14］SIMON M，ALOUINIM.Digital Communication over fading channels［M］.2ndedition.Chichester，U.K.:Wiley，2005.

(编辑:魏琴芳)