基于原模图LDPC 码的不等保护传输性能研究
聂浩斌,何继光,王 琳
(1.重庆邮电大学重庆市移动通信重点实验室,重庆 400065;2.厦门大学通信工程系,福建厦门 361005)
0 引言
在许多通信系统中,所传输的数据有不同的错误敏感度。对噪声特别敏感的部分重要信息,在传输过程中需实行重点保护,而对噪声不是特别敏感的次要信息则可以在传输过程中实行较少的保护来节省传输带宽和功率。在信道编码领域内,关于数据的不等错误保护,一直是应用价值比较高的研究课题。不等错误保护(unequal error protection,UEP)对于网络传输和视频传输中重要数据的保护都有重要意义。尤其是在多媒体通信当中,数据帧头包含的控制信息一旦出错,可能导致这一帧的数据传送失败,保护帧头显得格外重要。假若对全部信息采用等价保护则是一种功率浪费,因此,采用不等保护方案可以有效地节省功率。1967年,Masnick和Wolf等[1]人最先介绍不等错误保护码。之后,使用其他方法得到的不等保护码被相继提出[2-3]。近几年对多级编码、Turbo码等编码方案中的不等错误保护都有研究[4-6]。自 UEP码提出以来,关于 UEP方案的实现有很多途径,比如通过有目的地设计调制中的信号星座实现UEP,利用高阶调制中一个信号星座点的高低比特位的不同误码性能来实现,高比特位能够获得比低比特位更好的错误性能。有些信道码[7-8]本身就具备不等保护特性,具有不同连接度的节点,误码性能不一样,对于变量节点,连接度越高,误码性能越好。另外,分层调制结合不同的前向纠错码能够提供更好的误码性能[9]。
本文将性能比较优越的原模图LDPC码(protograph low density parity check code)[10]与4PAM(pulse amplitudemodulation)调制相结合,实现传输数据的不等保护,并与基于规则LDPC码的系统传输性能进行比较。结果表明,当码长较小时,原模图LDPC码的误码性能与规则LDPC码的误码性能相当。在误码率(bit error rate,BER)为 10-6数量级时,码率为1/2,码长为256的AR4JA码高比特位误码性能比(3,6)规则LDPC码差0.35 dB,低比特位误码性能比(3,6)规则LDPC码差0.4 dB。BER为10-6数量级时,码率1/2,码长为512的AR4JA码高比特位误码性能比(3,6)规则LDPC码差0.05 dB,低比特位误码性能比(3,6)规则LDPC码差0.2 dB。随着码长的增加,原模图LDPC码性能优于(3,6)规则LDPC码。对大原模图中每个同类型的q条边用一个交织器进行重排,经过交织后得到的原模图就是导出图,导出图与LDPC码的因子图其本质是一样的。从导出图产生的整个过程可以看出,基础矩阵B和扩展规则是影响原模图LDPC码性能的2个主要因素。在本文之后的讨论过程中,都假设扩展规则为文献[11]中的改进型的PEG(progressive edge-growth)算法。
下面给出原模图LDPC码因子图的生成过程,如图1所示。考虑图1a所示的原模图,基础矩阵为B。图1a经过q=2次重复后得到图1b,之后对图1b中相同类型节点间的边进行置换便得到导出图,如图1c所示,该因子图对应的LDPC码称为原模图LDPC码。通过改变q值,能够得到任意码长的原模图LDPC码。

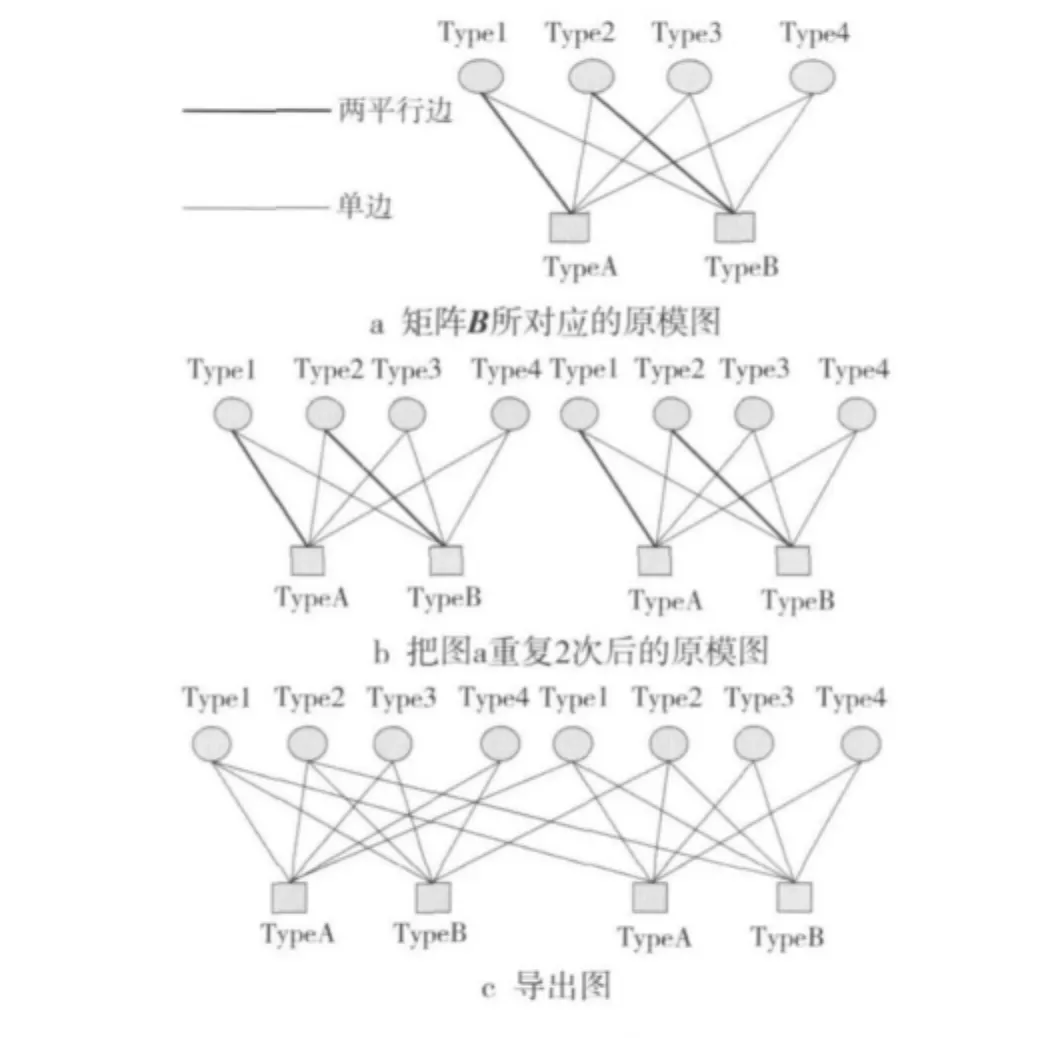
图1 原模图LDPC码因子图的生成过程Fig.1 Generate procedure of factor graph for protograph LDPC code
1 原模图LDPC码
LDPC码是一类由稀疏的校验矩阵(记为H矩阵)定义的线性分组码,每个校验矩阵都可由一个含有两类节点集合的Tanner图表示:一类为编码后比特的变量点集合,用V表示,另一类为校验约束关系的校验点集合,用C表示。由集合V,C以及这2类节点之间关联的边所组成的图形称为Tanner图。而原模图LDPC码可以看作一个由极少变量点和校验点构成的Tanner图。与LDPC码Tanner图的定义类似,原模图G=(V,C,E)也是由变量点集合V,校验点集合C以及连接变量点和校验点的边的集合E组成。原模图中的每条边e∈E分别连接一个变量点Vi∈V和一个校验点Cj∈C,每一条边都被看作一类边。在原模图中是允许平行边存在的,因此e→(Vi,Cj)∈V×C并不是一一映射的,原模图对应的校验矩阵称为基础矩阵,用B表示。
原模图LDPC码是与导出图相对应的LDPC码。导出图是由原模图经过重复后再对同类型的边进行交织后得到的,即首先对原模图重复q次,得到由q个相互独立的原模图组成的大原模图,之后再

2 系统模型
2.1 调制模型
在本文中,我们采用格雷映射的4PAM,如图2所示。星座信号定义为χ={-3,-1,1,3}。任意2个星座点之间的最小欧氏距离为 dmin。对于4PAM,bH表示星座信号点的高比特位,bL表示星座信号点的低比特位,bL和bH的BER为[12]


图2 格雷映射4PAM星座图Fig.2 Generalized 4PAM constellation with Graymapping
2.2 通信系统模型
4 PAM在加性高斯白噪声信道下的通信系统模型如图3所示,其中采用的映射器,我们使用格雷4PAM映射器,由信源产生的二元信号经编码器后产生编码码字,映射器将信号映射到信号星座点上(此前需将码字分解成上下支路信号来联合选择星座信号点),通过信道加噪后,迭代解映射器从信道接收到信号并进行解映射。最后对解映射器的软输出采用对数域BP算法进行译码。
2.3 软输出迭代译码
如果解码结果为软输出,如比特对数似然比,我们能够推导出如下迭代解映射算法。



图3 原模图LDPC码4PAM调制的系统方框图Fig.3 Systematic block diagram of protograph LDPC codeswith G4PAM
对于4PAM星座图,在加性高斯白噪声信道下,高低比特位对应的对数似然比分别为[13]

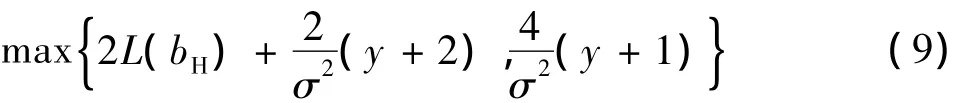
3 仿真结果与分析

分别经过64,128,256和1 024次扩展后经过删余操作得到码长为256,512,1024和4 096的AR4JA码,该码通过4PAM调制,得到高低比特位的误码率,并对仿真结果进行了进一步分析。仿真是在AWGN信道下进行的,译码算法采用对数域BP软输出迭代译码算法。
首先对码率R=1/2,信息长k=128的(3,6)规则LDPC码与信息长k=128的AR4JA码进行误码性能仿真,其高低比特位BER比较曲线如图4所示,(3,6)规则LDPC码和AR4JA码误码性能差别不大。在BER为10-6数量级时,码长为256的(3,6)规则LDPC码比码长为256的AR4JA码高比特位误码性能好约0.35 dB,(3,6)规则LDPC码低比特位误码性能比AR4JA码好约0.4 dB。

图4 码率R=1/2,码长为256的规则LDPC码与R4JA码高低比特位的BER性能曲线Fig.4 BER performance for high and low bits of regular LDPC codes and AR4JA codes with R=1/2,code-length 256
码率R=1/2,信息长k=256的(3,6)规则LDPC码与信息长k=256的AR4JA码高低比特位误码性能如图5所示,BER为10-6时,码长为512的(3,6)规则LDPC码高比特位性能相比AR4JA码差0.05 dB,低比特位误码性能比(3,6)规则LDPC码差0.2 dB。可见,在短的码长时,二者高低比特位误码性能相差不大。然而原模图LDPC码易用硬件实现结构简单的高速编码器。因此,在不等保护性能相当的情况下,可以选择原模图LDPC码来实现对重要数据实现更高级别的保护。
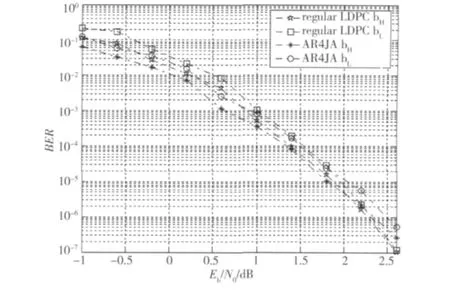
图5 码率R=1/2,码长为512的规则LDPC码与AR4JA码高低比特位的BER性能曲线Fig.5 BER performance for high and low bits of regular LDPC codes and AR4JA codes with R=1/2 and code-length 512
对于码长分别为1 024和4 096的AR4JA码和(3,6)规则LDPC码的高低比特位的性能曲线如图6和图7所示,从图6和图7中可以看出,在长码的情况下AR4JA码的不等保护性能要优于(3,6)规则LDPC码。因此对于长码,我们可以考虑使用原模图LDPC码来实现某些应用场合所需要的不等保护性能。
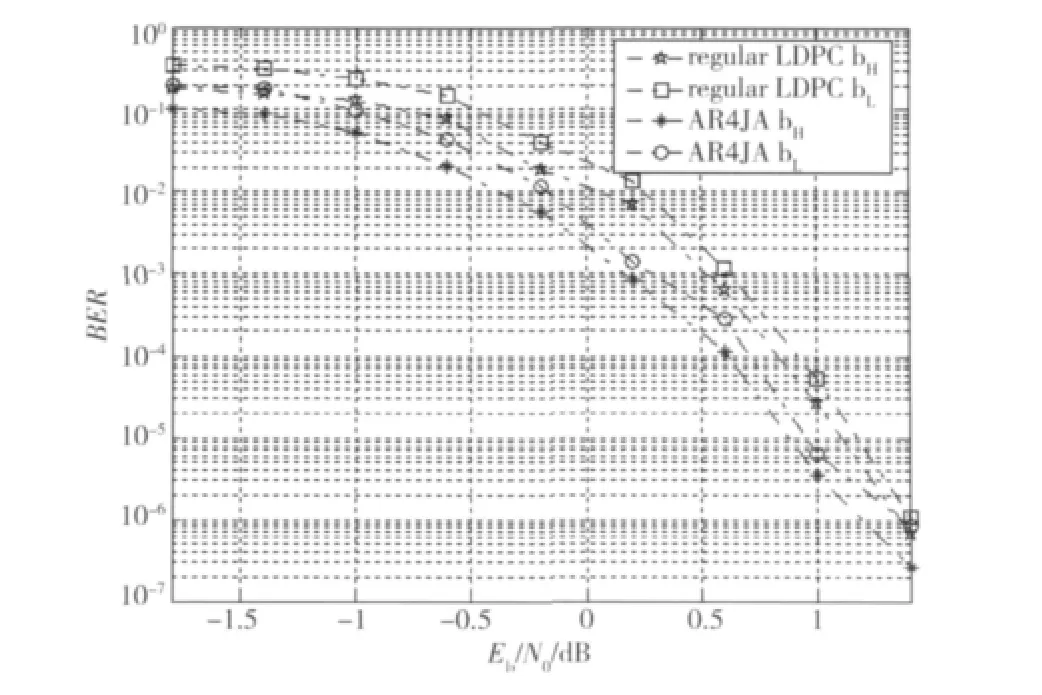
图6 码率R=1/2,码长为1 024的规则LDPC码与AR4JA码高低比特位的BER性能曲线Fig.6 BER performance for high and low bits of regular LDPC codes and AR4JA codeswith R=1/2 and code-length 1 024
另外,从所有仿真结果可以看出,低比特位BER大致等于两倍的高比特位BER。这一结果与理论值基本吻合。
4 结语
本文的主要目的是研究基于原模图LDPC码的不等保护传输性能。我们将4PAM与原模图LDPC码相结合来达到此目的。仿真结果表明这一方案不仅可以实现传输数据的不等保护,并且其不等保护性能在短码时与(3,6)规则LDPC码相当。在性能相当的情况下,由于原模图LDPC码编码更易于实现,码率可变等特性,利用原模图LDPC来实现不等保护可以减少硬件的复杂度。随着码长的增加,原模图LDPC码性能优于(3,6)规则LDPC码。
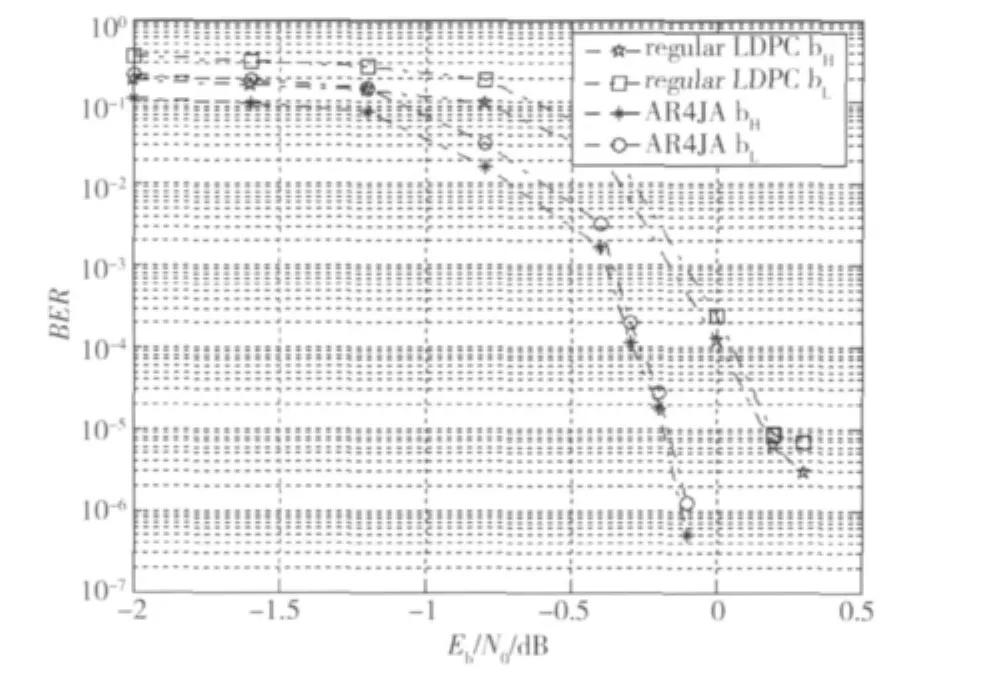
图7 码率R=1/2,码长为4 096的规则LDPC码与AR4JA码高低比特位的BER性能曲线Fig.7 BER performance for high and low bits of regular LDPC codes and AR4JA codeswith R=1/2 and code-length 4 096
[1]MASNICK B,WOLF J.On linear unequal error protection codes[J].IEEE Transactions on Information Theory,1967,13(4):600-607.
[2]KILGUSCC,GOREW C.Cyclic codeswith unequalerror protection[J].IEEE Transactions on Information Theory,1971,17(2):214-215.
[3]BOYARINOV I,KATSMAN K.Linear unequal error protection codes[J].IEEE Transactions on Information Theory,1981,27(3):168-175.
[4]BOYARINAOV IM,KATSM G L.Linear Unequal Error Protection[J].IEEE Transactions on Information Theory,1981,27(2):168-175.
[5]ISAKA M,FOSSORIERM PC,MORELOS-ZARAGOZA R H,et al.Multilevel Coded Modulation for Unequal Error Portection and Multistage Decoding-Part II:Asymmetric Constellations[J].IEEE Transactions on Communications,2000,48(5):774-786.
[6]刘军清,谢丹桂,郑胜.一种基于不等纠错保护的图像传输方法[J].电路与系统学报,2010,15(4):115-119.
LIU Jun-qing,XIE Dan-gui,ZHENG Sheng.An image transmissionmethod based-UEP[J].Circuit and System,2010,15(4):115-119.
[7]RICHARDSON T J,SHOKROLLAHIM A,URBANKE R L.Design of Capacity-Approaching Irregular Low-Density Parity-Check Codes[J].IEEE Transactions on Information Theory,2001,47:619-637.
[8]刘冰,高俊,陶伟,等.带宽有效传输下多进制LDPC码的不等错误保护[J].信号处理,2011,27(7):1088-1094.
LIU Bing,GAO Jun,TAOWei,et al.Unequal Error Protection Nonbinary LDPC Codes for Bandwidth Efficient Transmission[J].Signal Processing,2011,27(7):1088-1094.
[9]DEETZEN N V,SANDBERG S.Design of Band width-Efficient Unequal Error Protection LDPC Codes[J].IEEE Transactions on communications,2010,58(3):802-811.
[10]THORPE J.Low-density parity-check(LDPC)codes constructed from protographs[R].[s.l.]:IPN Progress Report,2003:42-154.
[11]BONELLO N,CHEN Sheng,HANZO L.Construction of regular Quasi-Cyclic protograph LDPC codes based on vandermondematrices[J].IEEE Transactions Veh Technol,2008,54(4):2583-2588.
[12]NIU Dimin,PENG Kewu,SONG Jian.LDPC Coded Modulation with Unequal Protection[C]//Communications,Circuits and Systems,2008.ICCCAS 2008.International Conference on. [s.l.]:Conference Publications,2008:114-118.
[13]XIEQiu-liang,PENG Ke-wu,SONG Jian.On the Channel Capacity and Iterative Demapping of Generalized 4PAMover AWGN Channel[C]//IEEE Singapore International Conference on Communication Systems.Singapore:Conference Publications,2008:860-863.
(编辑:魏琴芳)

