基于TDOA 的卫星干扰源定位方法的研究

郝才勇，刘 恒，刘宏立

(1.国家无线电监测中心深圳监测站，广东深圳 518000;2.湖南大学电气与信息工程学院，湖南长沙 410082)

0 引言

在卫星干扰源定位系统中，目前普遍采用的是基于到达时间差/到达频率差(time difference of arrival/frequency difference of arrival，TDOA/FDOA)的双星定位方法。该方法利用被干扰的卫星(主星)和满足定位条件的相邻卫星(邻星)，测量信号经过这2颗卫星转发后到达接收站的TDOA和FDOA，从而建立方程计算出干扰源位置。

双星定位方法的关键是获取准确的TDOA和FDOA值。研究发现［1］，定位误差中很大一部分来源于卫星星历中的速度误差，而星历中卫星位置的误差对定位精度的影响较小。卫星的位置决定了定位需要的TDOA值，因而TDOA值较为准确和稳定;卫星的速度决定了定位需要的FDOA值，速度的微小变化导致的定位误差可达到几百公里甚至上千公里［2］，因而FDOA值不稳定，难以准确测量。通常利用地理位置已知的参考站向卫星发射信号，接收站同时接收卫星转发的干扰信号和参考信号［3］，从而对卫星速度和频率差校准，但这需要多个参考站的参与，文献［4］研究表明至少有4个或以上参考站才能较好地消除星历不准确对定位精度的影响。此外，采用多个参考站仍然很难对卫星速度做出准确的预测，定位精度不太理想(参考站数量大于4个时，定位精度为30 km)。在对某个卫星信号定位时，有时难以找到4个或以上的参考站，导致定位误差进一步增大。同时定位精度还受到定位时段的影响，每天有2个时段，2颗卫星的相对位置会导致FDOA测量值的误差很大，定位精度严重恶化［1］，这段时间出现的干扰信号难以定位。

本文提出了基于TDOA的卫星干扰源定位方法，去除了导致定位误差较大的FDOA，仅采用TDOA，在单参考站条件下实现高精度卫星干扰源定位，且定位精度不受参考站数量和定位时段的限制。研究了TDOA卫星干扰源定位原理和定位算法，提出了信赖域算法实现定位，通过实测的数据进行实验来验证定位方法;最后，对定位精度和定位结果的有效性进行了分析。

1 TDOA定位原理

假设空间静止轨道上的3颗卫星:主星、邻星1和邻星2分别接收地面干扰源发射的信号，接收站测量经过这3颗卫星转发信号的到达时间，得到2组独立的时差TDOA。每一组独立的时差定义的方程在空间中确定了一个双曲面，另外，目标干扰源位于地球表面上，与空间双曲面相交可分别得到2条双曲线。这2条双曲线的交点就是目标干扰源的位置，如图1所示。

图1 TDOA卫星干扰源定位原理Fig.1 TDOA satellite interference locatingmethod

假设地球为标准椭球，干扰源的坐标为rm(x，y，z)，3 颗卫星的坐标分别为 r1(x1，y1，z1)，r2(x2，y2，z2)和 r3(x3，y3，z3)。卫星信号接收系统采集目标信号，对经过主星和邻星转发的2个信号做互相关运算和参数估计［5］，得到信号通过主星和邻星转发到达接收站的时差。假设信号经过主星分别和邻星1、邻星2转发得到的时差分别为△t1和△t2。则根据3颗卫星的几何关系，可得到时差方程为

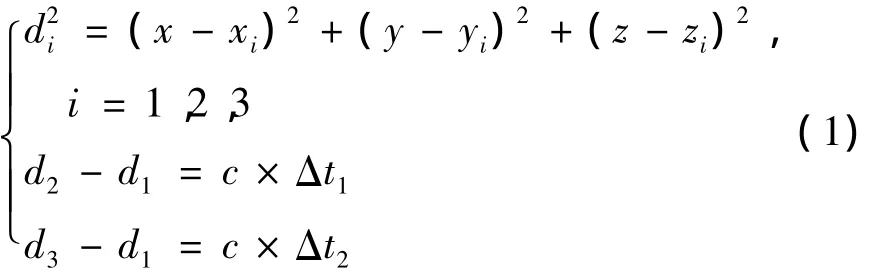
(1)式中:xi，yi，zi分别为第i颗卫星的空间位置坐标;di为第i颗卫星到干扰源的距离;c为电磁波传播速度。

地球模型采用WGS－84地球椭球模型(大地坐标系)［6］，表示为

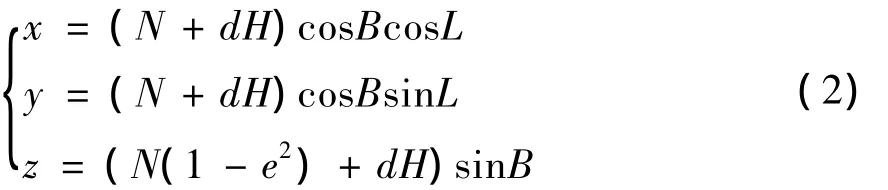
(2)式中:N=a/(1－e2sin2B)1/2，N为目标当地卯酉圈半径;L，B，dH分别为目标的经度、纬度和高程;a为地球长半轴;e为地球椭球第一偏心率。研究表明［7］:当目标高程较小(小于200 m)时，将高程设为0对于随机偏差的影响可以忽略。因此，可以假设高程dH=0，设地球短半轴为b，则(2)式可表示为椭球方程

由(1)式和(3)式可以求出目标干扰源的空间坐标rm(x，y，z)，然后将空间坐标系向经纬度坐标系变换，就可以计算出目标的经纬度位置。

2 TDOA定位算法

联立时差方程(1)和地球椭球模型方程(3)得到TDOA定位方程组

对(6)式的非线性方程组，采用信赖域算法求其最优化解。信赖域算法是求解非线性优化问题的一类重要的数值计算方法，具有很强的收敛性和可靠性。其基本思想是:设xk是当前迭代点，在以xk为中心，rk为半径的邻域内求解子问题，要求试探步长dk在信赖域内，即在每次迭代时有一正数rk，要求试探步长满足|dk|rk，用评价函数来决定dk是否被接受，若被接受，则令xk+1=xk+dk;否则令xk+1=xk，如果试探成功，信赖域半径保持不变或扩大，否则缩小半径［8］。当函数值收敛为满足精度的极小值时，迭代完成。表1为使用信赖域算法解方程(6)得到的一组迭代结果。

表1 信赖域算法迭代结果Tab.1 Results of trust－region method

从迭代结果可以看出，对给定的初值和初始信赖域半径，经过18次迭代之后函数急剧收敛。迭代达到22次时，函数F(x)达到精度要求，迭代完成。此时方程(6)的解为干扰目标在地球表面的位置。

3 定位试验

为了验证TDOA方法实现卫星干扰源定位的有效性和可靠性，并分析定位精度，采用实测的卫星数据进行干扰源定位实验。实验平台采用卫星干扰源定位系统，其中包括高增益卫星接收天线系统、数据采集系统、时差/频差数据相关和参数估计处理系统等。将已知发射源位置的某信号作为干扰目标，卫星星历采用国际卫星组织最新发布的数据，试验条件如表2。

表2 定位试验条件Tab.2 Locating experiment conditions

(7)式中:s1为经过主星转发信号的包络;(t+τ)为经过邻星i转发信号的复包络;s2，s3为经过邻星1和邻星2转发信号的包络;T为相关累积时间;τ和f分别为时差TDOA(Δt)和多普勒频差FDOA，由于在TDOA定位中，不需要使用频差，故此处不关心f的取值。经过对2组信号的接收，使用CAF分别得到互模糊函数A1(τ)，A1(τ)的峰值，即可求出△t1和△t2，代入(4)—(6)式，即可计算出目标定位点的位置。对表2给出的试验条件，使用TDOA定位方法得到的定位结果如图2所示。

目标信号经过3颗卫星转发后到达接收站，卫星干扰源定位系统以时分复用的方式分别接收主星－邻星1和主星－邻星2的信号，变换到中频后进行数据采样，使用互模糊函数［9］(cross ambiguity function，CAF)分别求出2路信号的TDOA值为

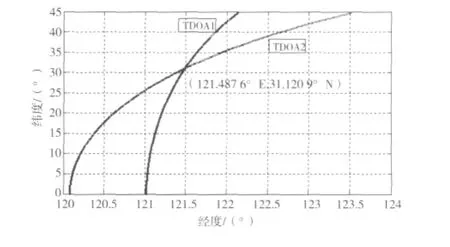
图2 实测数据定位结果Fig.2 Locating results of themeasured data

图2中使用TDOA方法定位得到的目标位置为(121.487 6°E，31.120 9°N)，距离目标的真实位置误差仅为4 km，相对于双星定位系统在至少4个参考站的条件下，定位误差为30 km(在单参考站情况下，TDOA/FDOA方法的定位误差为几百公里)的精度有了显著的提高。

为了进一步验证TDOA定位方法在单参考站条件下，定位精度高的可靠性和有效性，在同一实验条件下(主星、邻星相同，目标信号相同，星历相同，定位时段相同，参考站、接收站相同，采样带宽、采样时间相同)，分别使用TDOA定位方法和TDOA/FDOA方法对同一目标信号进行定位。在表2的定位实验条件中，选择5组不同的目标信号，其他参数保持不变，分别计算出2种方法下的定位结果和定位误差。TDOA/FDOA目标定位位置和误差表示的是主星分别和2颗邻星(邻星1、邻星2)得到的2次定位结果。数据采集时间为2011年3月16日12时05分，定位结果如表3所示。

表3 相同目标信号定位结果比较Tab.3 Comparison of the same target signal locating

从表3可以看到，在相同实验条件下进行的多次定位实验中:TDOA定位方法的定位精度均保持在几公里级，其中第4组数据误差较大，这是由于数据采集误差造成的，在可接受范围内(＜10 km);TDOA/FDOA定位方法的平均误差为401 km，而TDOA定位方法的平均定位误差仅为3.3 km。实验结果说明了TDOA定位方法具有可靠性;相对于TDOA/FDOA定位方法，TDOA定位方法在定位精度上提高了2个数量级。

4 误差分析

对于给定的星历，使用一定的采样带宽，可测量出TDOA时差线在地球表面偏移目标点距离的范围。表4为试验参数设置，其中115.5°E为主星经度，122.2°E为邻星经度。表5给出的是已知目标发射源到地球表面上TDOA时差线最近点(表4中的目标实际位置)的距离，距离值就是单条TDOA时差线的定位误差。

表4 TDOA时差线定位参数设置Tab.4 Locating parameters settings of TDOA line

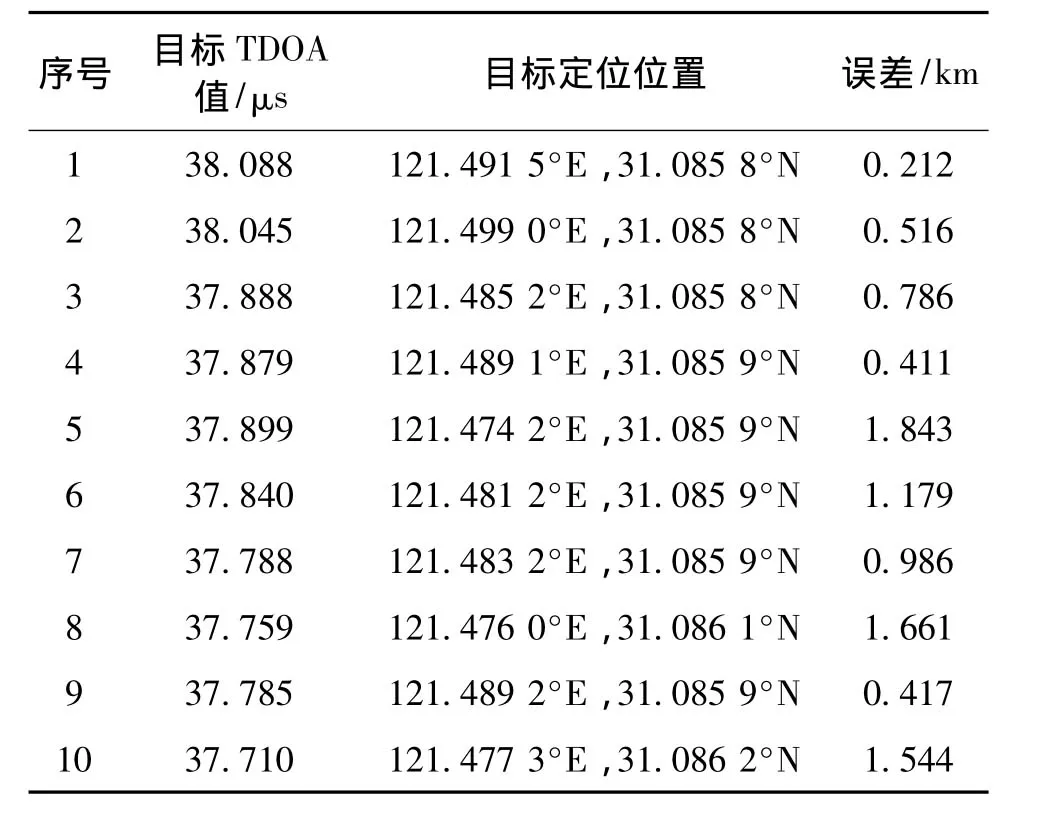
表5 TDOA时差线定位误差Tab.5 Locating errors of the TDOA line

在表4测试条件下，由表5可以得到时差位置线距离干扰源的平均误差为0.955 5 km，其中最大误差为1.843 km。

TDOA定位干扰源的误差由2条时差线偏移干扰源的距离和它们的相交角度决定，其定位误差范围如图3所示的菱形区域。

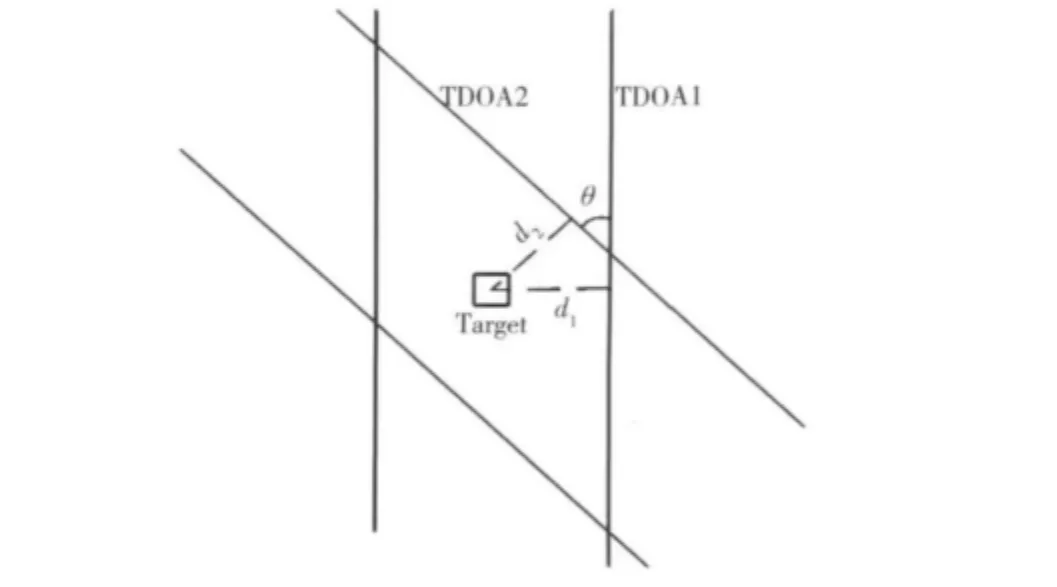
图3 TDOA定位误差范围Fig.3 Error range of TDOA locating

由表5得到的结果，取d1=d2=0.955 5 km，代入(7)式，则误差范围为:e(d1，d2，θ)≥3.652 km2，当 θ=7°时，误差范围为29.967 km2。说明当时差线的夹角大于7°时，能够满足定位误差范围小于30 km2的精度，且随着夹角θ的增大，定位误差范围逐渐减小，当θ=90°时，定位误差范围最小，仅为3.652 km2。

图3中，Target表示目标位置;d1，d2分别为2条时差线到干扰源的距离误差;θ为时差线的夹角。则定位误差范围可表示为

5 结论

基于TDOA卫星干扰源定位方法去除了导致定位误差较大的多普勒频差FDOA的影响，具有定位精度高、仅需单参考站定位条件并且不受定位时段影响等优点，其代价是需要2颗邻星。本文研究了TDOA卫星干扰源定位原理和定位算法，通过实测数据进行试验，验证了定位的可靠性，分析了定位误差，证实了该方法相对于TDOA/FDOA双星定位系统中采用单参考站时的定位精度提高了2个数量级，实现了对卫星干扰源准确有效的定位。

［1］HAWORTH D P，SMITH N G，BARDELLIR，et al.Interference localization for EUTELSAT satellites－the first European transmitter location system［J］.International Journal of Satellite Communications，1997，4(15):155－183.

［2］RICCARDO B，DAVID H，NIGEL S.Interference localization for the EUTELSAT satellite system［C］//IEEE.IEEE Globecom'95.Singapore:IEEE Press，1995，11:1641－1651.

［3］夏畅雄，叶尚福，王俊辉.卫星干扰源定位系统中卫星星历校正技术［J］. 宇航学报，2008，29(3):860－863.

XIA Chang－xiong，YE Shang－fu，WANG Hun－hui.Ephemeris Determination in Satellite Interference Location System［J］.Journal of Astronautics，2008，29(3):860－863.

［4］瞿文中，叶尚福，孙正波.卫星干扰源精确定位的位置校正算法［J］.电波科学学报，2005，20(3):342－346.

QUWen－zhong，YE Shang－fu，SUN Zheng－bo.Algorithm of position calibrator for satellite interference location［J］.Chinese Journal of Radio Science，2005，20(3):342－346.

［5］马金明.TDOA参数估计算法［J］.北京邮电大学学报，2007，1(30):96－99.MA Jin－ming.Research on TDOA Estimating Algorithms［J］.Journal of Beijing University of Posts and Telecommunications，2007，1(30):96－99.

［6］GUO Fu－cheng.Single Satellite Direction－Finding Localization Method Based on WGS－84 Earth Model［J］.Journal of Astronautics，2011，32(5):1179－1183.

［7］钟丹星，邓新蒲，周一宇.基于 WGS－84椭球模型的卫星测时差定位精度分析［J］.电子对抗技术，2002，5(17):18－21.

ZHONG Dan－xing，DENG Xin－pu，ZHOU Yi－yu.Precision Analysis of Satellites DTOA Location Based on WGS－84 Ellipsoid Model［J］.Electronic Warfare Technology，2002，5(17):18－21.

［8］薛西峰，邢志东，孟红云.求解非线性方程组的信赖域算法［J］.西北大学学报，2001，4(31)，289－291.

XUE xi－feng，XING Zhi－dong，MENG Hong－yun.Trust region method for sloving nonlinear equations［J］.Journal of Northwest University，2001，4(31)，289－291.

［9］SAY Song Goh，GOODMAN TN T，SHANG F.Joint Estimation of Time Delay and Doppler Shift for Band－Limited Signals［J］.Signal Processing，2010，9(58):4583－4594.

(编辑:王敏琦)