基于多周期条纹投影技术的位相逆推法在物体表面形状测量中的应用

宦 海，张思俊，陆振宇

(南京信息工程大学电子与信息工程学院，江苏南京 210044)

0 引言

摩尔条纹和条纹投影技术都是光学非接触测量技术，被广泛应用于测量物体三维表面形状［1］。在实验中，将条纹投影在物体表面，通过电荷耦合元件(charge－coupled device，CCD)检测物体表面产生形变的条纹，利用相移测量方法［2］或傅里叶变换法［3］计算出条纹的位相分布，最后通过分析条纹的位相分布特征得到物体的表面形状。由于通过计算得到的位相分布在－π～+π之间，所以必须应用空间位相解包裹法来复原物体表面形状。空间位相解包裹法是通过比较相邻两点的位相差来解包裹的，这就要求两相邻点的位相差不能大于2π，因此普通的条纹投影法不能用于测量非连续表面形状。

最近，学者们提出了一些新的条纹投影方法，并以此来测量非连续物体表面形状。这些方法或采用大周期条纹投影技术，或采用类似于多波长干涉技术的多周期条纹投影法［4－6］。在位相解包裹时采用大周期条纹投影法可以使相邻两点间位相跳变小于2π，从而解决非连续表面形状的测量问题。但是使用大周期条纹投影法的测量精度不高，所以研究者希望能够用小周期的条纹投影来测量不连续表面形状。根据这个思路，文献［7］提出了一种简单的方法:使用两个不同周期的条纹来测量物体表面形状;文献［8］中提出了一个改进的方法:使用几个不同周期的条纹投影来测量非连续表面形状。这些方法通过分析在不同周期条纹投影下，测量点的光强或位相变化来得到物体的表面形状，该方法具有较高的测量精度。本文介绍了一种基于正弦波位相调制干涉仪的多周期条纹投影方法［9］，并通过此方法来测量物体的表面形状。实验中检测到的条纹强度和位相分布在物体表面产生对应于不同条纹周期的检测光场，由于在条纹周期扫描中固定位相点的光场不变化，所以物体表面上每一点的光场都能逆推到固定位相点。当逆推场达到固定位相点时，不同条纹周期逆推场和的振幅变为最大值，同时位相变为0。物体表面每一个点到固定位相点的逆推距离决定了物体表面的位置。这种方法就被称为位相逆推法［10－12］。

此外，基于多周期条纹投影干涉技术的位相逆推法还可以应用在测量物体两个表面位相上。在透明物体表面的测量中，物体正面和背面测量点的位置使得逆推场的振幅有两个峰值，并且其对应的位相值均为0，因此采用上述位相逆推法可以同时确定上下表面两个点的位置。数值模拟和实验证实:在测量范围为毫米级时，基于多周期条纹投影法的位相逆推法测量精度可以达到微米级。

1 多周期条纹投影干涉仪和位相逆推法

多周期条纹投影干涉仪的示意图如图1所示。两个沿不同方向上传播、波长为λ的平面波在空间中产生了一组平行的干涉条纹。如图1所示，建立坐标系统(xp，yp，zp)。两个平面波的传播方向与zp轴的夹角为±θm，条纹的周期可用 Pm=λ/2θm来表示，当 θm很小时，sinθm≈θm。改变夹角 θm为 θ0，θ1，…，θM－1，相应地，条纹周期 Pm变为 P0，P1，…，PM－1。通过使用反馈控制系统，使得在周期扫描时，在xp=0的位置上，干涉条纹的位相保持在π/2不变。在坐标系统(xp，yp，zp)中，位相分布可写为(1)式中，km=为条纹的波数。

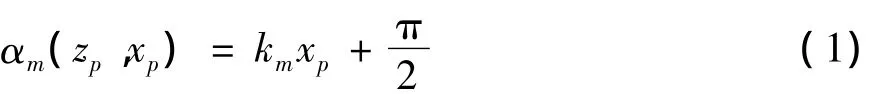
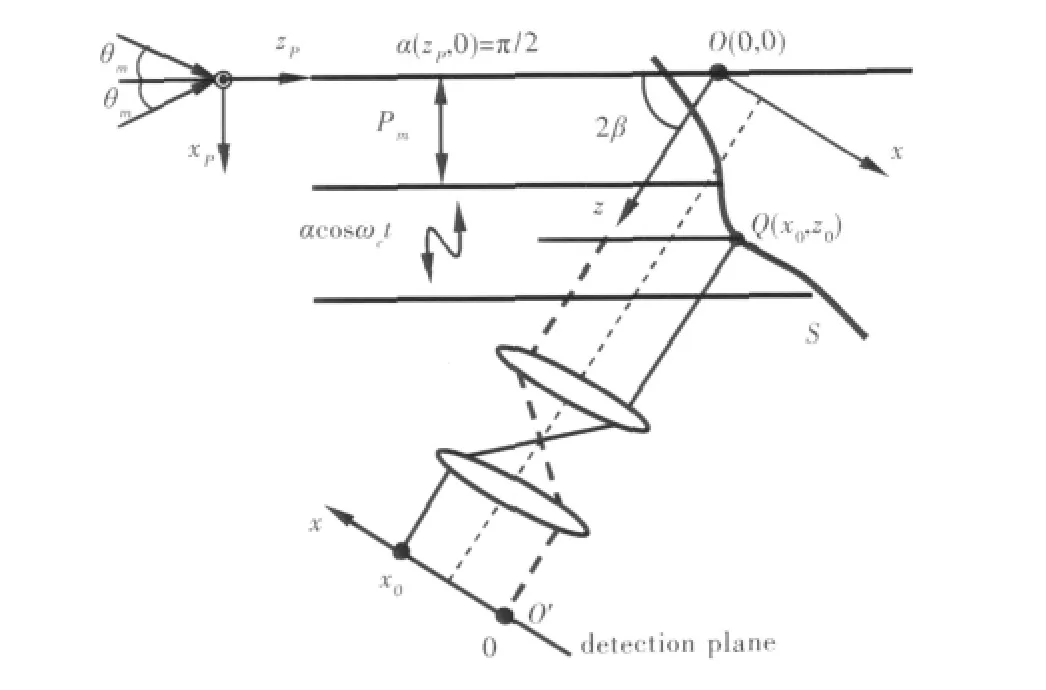
图1 采用正弦波位相调制的多周期条纹投影法示意图Fig.1 Schematic configuration formulti－period fringe projection and detection of the fringe patterns by sinusoidal phase－modulating interferometry

假设在物体表面上有一点Q，通过共焦点成像系统在检测平面上形成该点的像。在成像系统中定义另一个坐标系统(x，y，z)，坐标系统(x，y，z)的原点O与坐标系统(xp，yp，zp)的原点相对应。z轴平行于成像系统的光轴。zp轴与z轴的夹角为2β。坐标系统(x，y，z)的位相分布可写作为

为了引入正弦波位相调制干涉，使干涉条纹的强度沿xp轴方向以a cosωct的形式进行正弦振荡，其中ωc代表频率。随后在探测端面上检测出Q点产生的干涉信号

通过正弦波位相调制法计算得到干涉信号的幅度Bm和位相αm，αm(x0，z0)的计算值介于－π和π之间［9］。由于在条纹周期扫描中，探测点的横坐标x是由固定位相点所决定的，当条纹周期变化时，固定位相点的位相保持π/2不变，所以探测端面的位置决定了物体的坐标 x0。计算出 αm(x0，z0)减去kmx0cos2β+π/2的值，可以得到位相αmz

由于已经从共焦点成像系统的对应关系中得出物体的坐标x0，接下来利用位相逆推法求物体的坐标z0。在位相逆推法中，Q点的检测域由下式所决定

2 位相逆推法的仿真数值分析

如图2所示为位相逆推法的数值仿真结果。条纹的扫描周期从200～400 μm，M=6，Δk=0.003 1 rad/μm，β=45°，zmax=2 000 μm。设定 z0的值为1 525 μm。假设对于所有的Pm，干涉信号的振幅Bm均为1。从图2可以得出，当周期PC为266.7μm时，UR的振幅分布AR在z=zA处有最大值，并且位相分布φR在z=zφ处等于0。若位相测量值没有受到噪声影响，则zA和zφ的值等于点状目标物的位置z0。

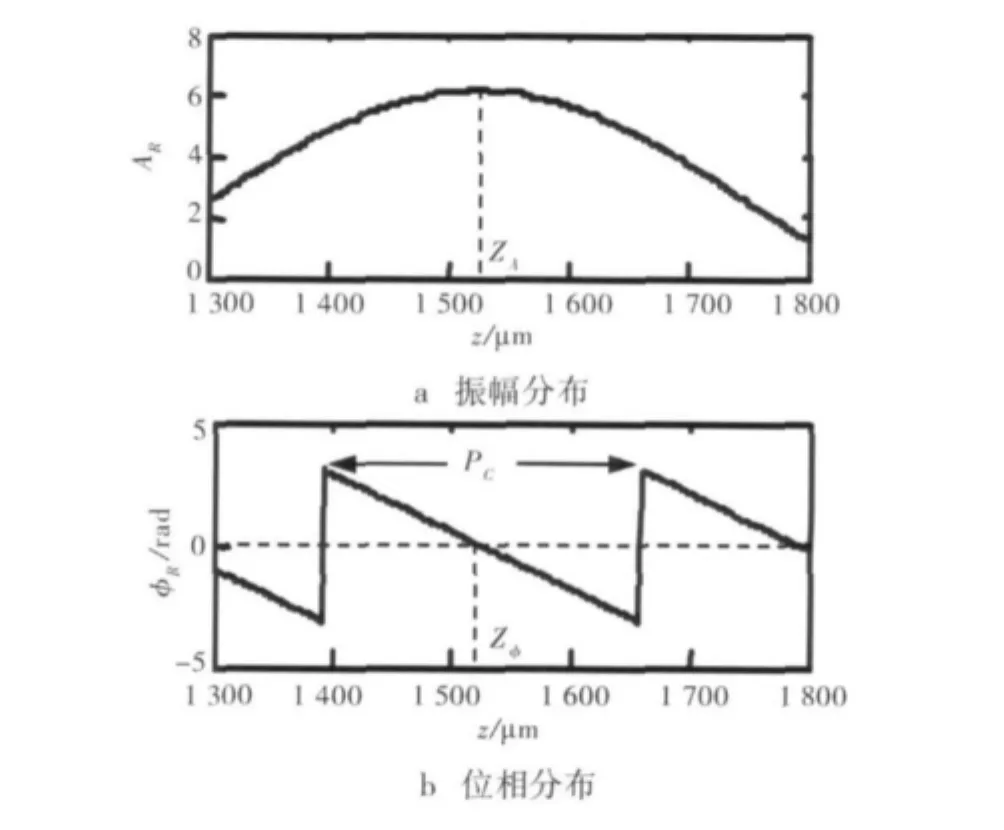
图2 物体表面某点的位相逆推法仿真结果Fig.2 Simulation results of the back－propagation method for one point object

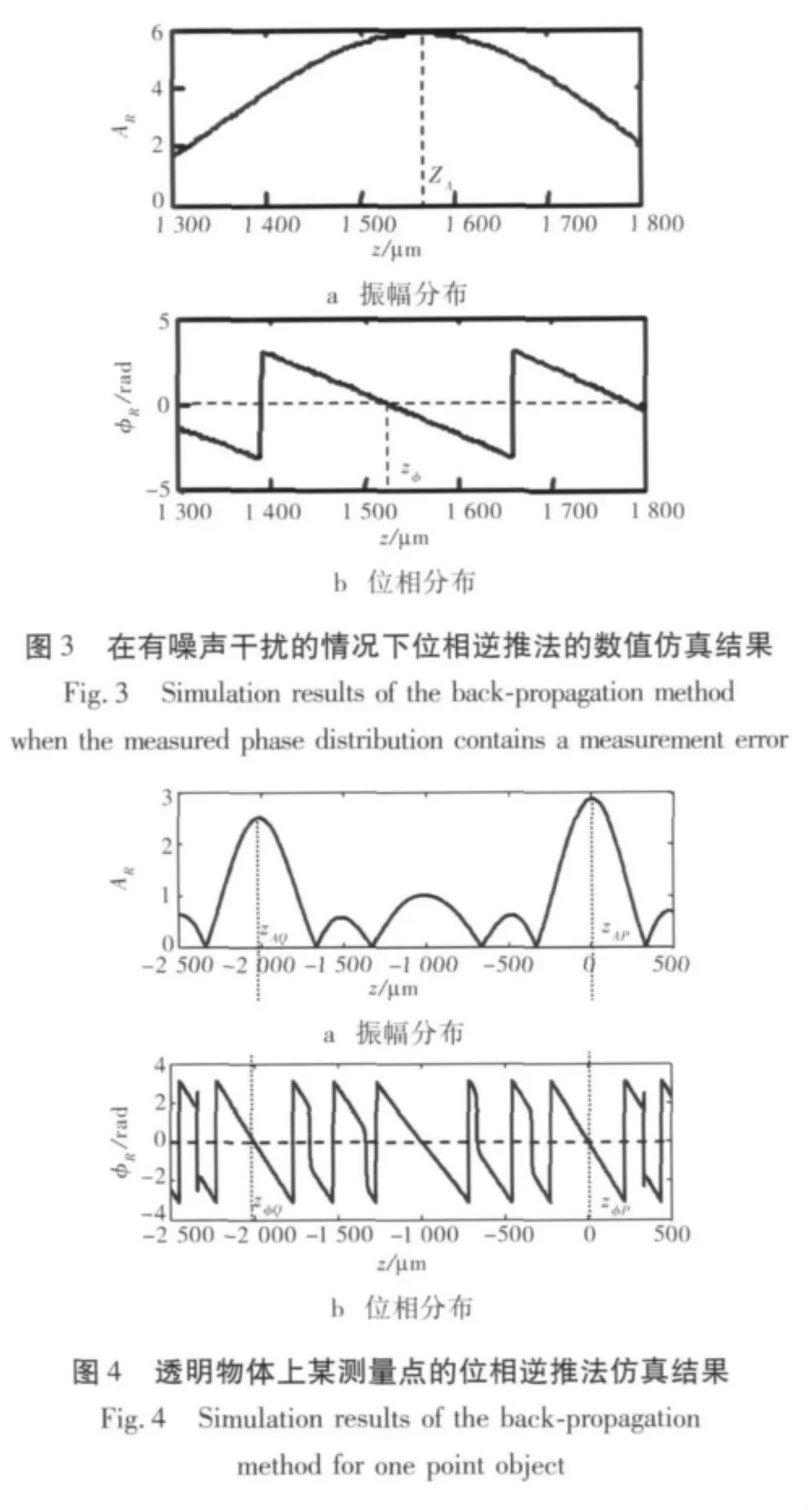
假设其他仿真条件不变，测得的位相分布αm受到一个随机噪声的影响，设随机误差符合正态分布，其平均值为0且标准偏差为σ。在σ=0.36 rad时，仿真结果如图3所示，在这种情况下，zA和zφ的值相对于z0的真实值都产生了误差，其中zA=1 579μm，zφ=1 531μm。通过仿真可以得出:当测量到的位相分布存在噪声影响时，逆推法得到的位相测量值和振幅测量值同时受到噪声的影响，但是位相测量值zφ比振幅测量值zA更精确，所以在实际测量中采用由位相值所得到的测量值。

图4为透明玻璃板表面上某一点的位相逆推仿真结果。条纹的扫描周期从140μm到800μm，M=18，Δk=0.002 2 rad/μm，β =30°，n=1.5。平板的厚度是2 830μm。玻璃板两个表面的位置z1和zQ的值分别为0μm和－2 000μm。假设对于所有的Pm，干涉信号的振幅Bm均为1。由图4可知，UR的振幅分布AR在z=zAP和z=zAQ处有最大值，同时其位相分布 φR在 z=zφP和 z=zφQ处为 0，其中周期 PC为476.6μm。由仿真结果可以得到:zAP=5μm，zAQ=－2 010 μm，zφP=2 μm，zφQ= －2 004 μm。因此，采用位相逆推法可以同时测量透明物体两个表面的位置坐标，并且位相值得到的结果精度高于振幅值得到的结果。

3 实验

3.1 实验装置

实验装置如图5所示，使用一个50 mw的激光二极管作为光源。光源发出的激光经过透镜L0准直后被分束器BS1分成两束激光，经M1和M2反射后形成干涉条纹。通过压电换能器PZT1改变镜子M1的角度θ，从而改变干涉条纹的周期Pm。压电换能器PZT2以fc=125 Hz的频率振动，用于在干涉条纹中引入正弦波位相调制。干涉条纹被分束器BS2分成两部分，一部分被光电二极管 PD接收，用于检测xf点的干涉信号，继而进行反馈控制。综合考虑式(1)和式(3)，检测到的干涉信号可写为

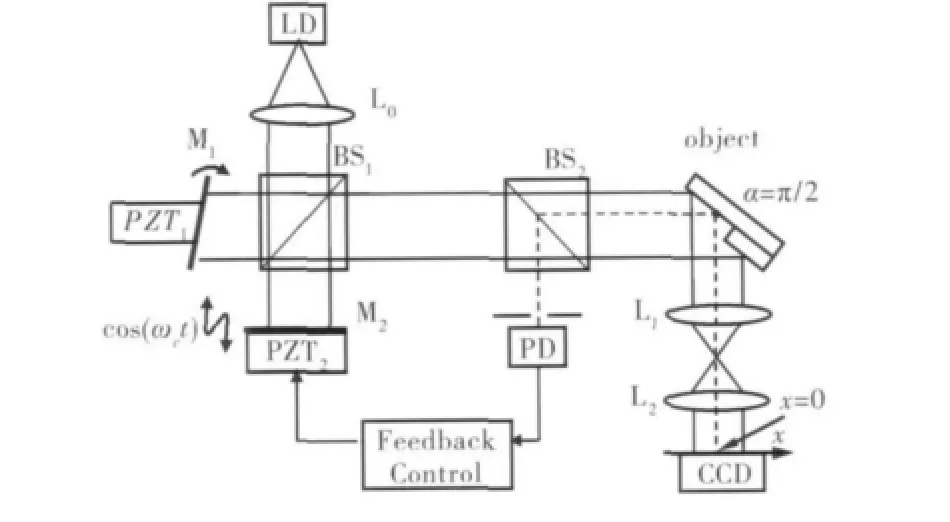
图5 多周期条纹投影法测量物体表面形状的实验装置Fig.5 Experiment setup of themulti－period fringe projection for surface profilemeasurement

在反馈控制电路中，滤除直流成分Am并且在cos(ωct)=0时刻对信号Im(t，xf)进行采样，得到反馈信号Sf=Bmcos(kmxf)，将由信号Sf产生的反馈控制信号作用于PZT2上，通过移动镜子M2，使Sf变为0。当干涉条纹的周期Pm发生改变时，反馈控制系统将点xf的位相固定为π/2。xf点定义为xp轴和x轴的原点，表达式(1)成立。

将干涉条纹的另一部分投影到被测物体表面，经共焦点成像系统成像于检测面上。该成像系统的放大率为M12=f2/f1，其中f1和f2分别为L1和L2的焦距。采用帧周期为1 ms的高速CCD照相机检测经正弦波位相调制后的干涉条纹。当被测物体是一面镜子时，CCD照相机检测到的条纹如图6所示。

图6 待测物体为一面镜子时检测到的干涉条纹Fig.6 Detected fringe pattern when object is amirror

3.2 实验结果

3.2.1 两个标准块构成的阶梯状光学表面的测量结果

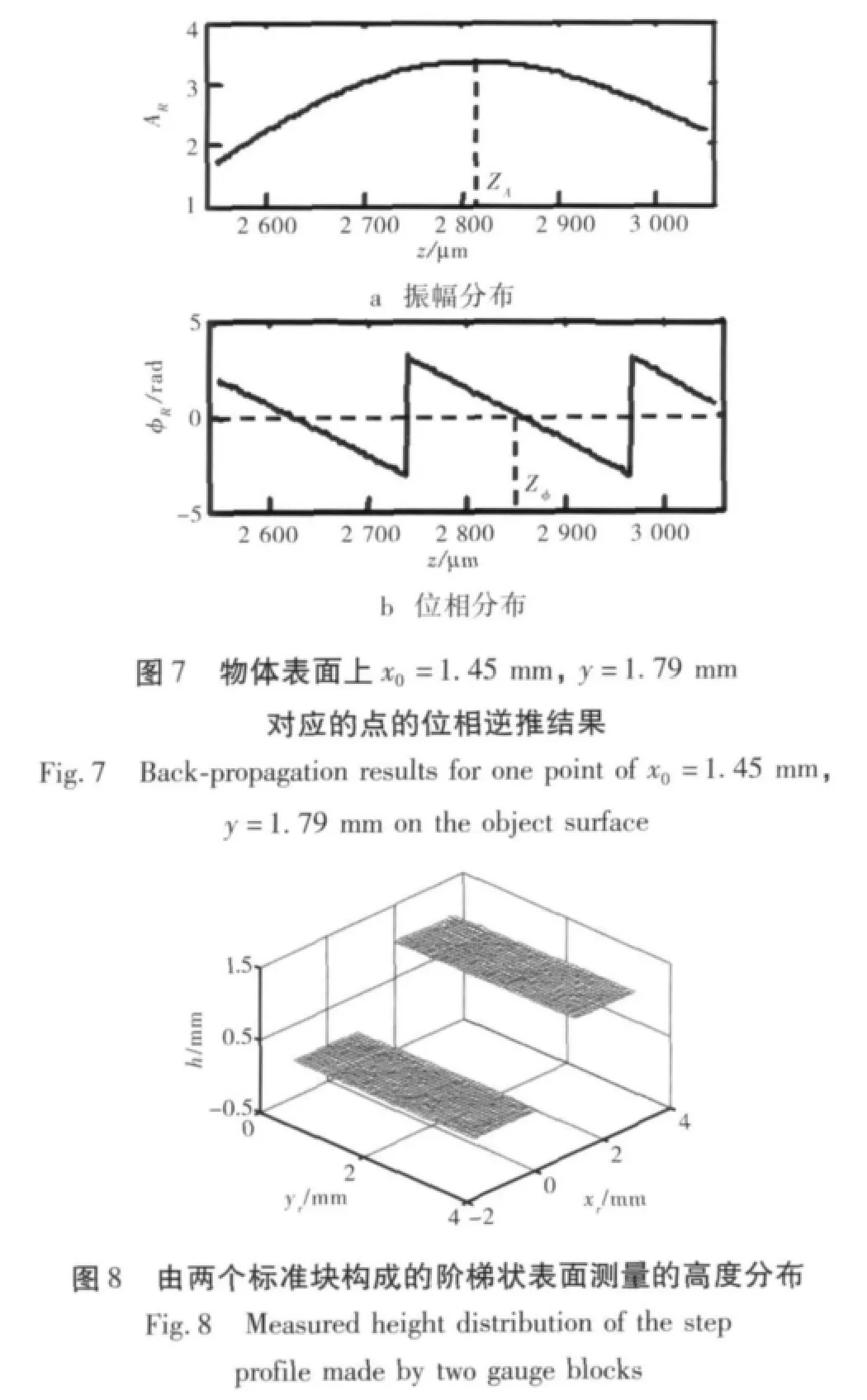
首先，将两个标准块构成的阶梯状光学表面作为待测物体。阶梯状物体高H为1 000μm，实验设备的相关参数如下:P1=249.8μm，P2=285.2μm，P3=332.6 μm，P4=400.3 μm，Δk=0.003 1 rad/μm，β=45°，zmax=2 000 μm，PC=266.7 μm，f1=100 mm，f2=50 mm。电荷耦合元件(charge－coupled device，CCD)所获取的图像大小是256×240像素，每个像素尺寸为7.4μm。因为M12=1/2，所以物体表面的测量面积约为3.8×3.6mm2。图7所示为物体表面上x=1.45mm，y=1.79mm测量点的振幅AR和位相φR，从测量结果可以看出，zφ的测量值为2 862μm。计算得到该点处h的值为998μm。图8和图9所示分别为在参考平面上测量的高度分布h和在y=1.79 mm横截线上测得的高度分布h，xr表示参考平面的横坐标。由于阶梯状被测物在条纹投影时会产生阴影，所以在xr=0.98mm到xr=1.95 mm的范围内得不到相关的测量信号。在y=1.79 mm的这条横截线上高度差h的平均值为998μm，每隔若干分钟重复测量。测量的重复误差大约是2.5μm。

3.2.2 2 mm厚玻璃板的测量结果

将2 mm厚玻璃板作为测量对象。实验相关参数如下:P1=143.0 μm，P16=1 002.4 μm，M=16，Δk=0.002 3 rad/μm，zmax=3 mm，β =45°，f1=100 mm，f2=25 mm。CCD所获取的图像大小是256×240像素，每个像素尺寸为7.4μm。因为M12=1/4，所以物体表面的测量面积约为7.4×7.2mm2。图10所示为玻璃板正面上x=2.90 mm，y=3.58 mm测量点的振幅AR和位相φR。分析可知，zAP和zAQ的测量值分别为－2 128μm和16μm，玻璃板厚度d的测量值为2 005μm。检测任意其他两个测量点，测量结果如表1所示。很明显，由位相分布得到的测量值精度要比振幅分布得到的测量值精度高。图11为玻璃板两个表面的测量位置，其中为了显示两个表面的形状分布，z轴是不连续的。厚度测量值d的平均值是2 001μm。每隔几分钟重复测量，共测量3次。重复测量误差约是2.5μm。由于玻璃板的两个表面是平行的，所以图11所示的形状也可看作是位相逆推法的测量误差。由实验结果分析可知，表面的波动约为2.8μm，所以位相逆推法的测量误差约为2.8μm。

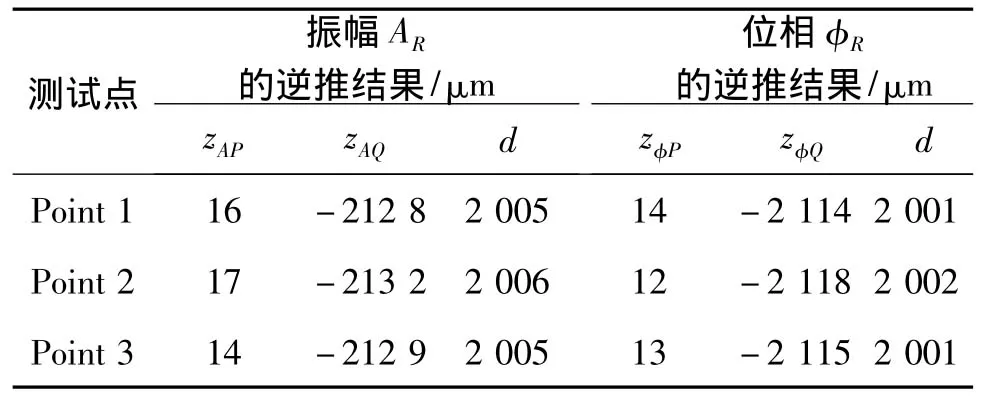
表1 表面3个点测量结果的比较Tab.1 Comparison ofmeasurement result of three points on the surface

图11 2 mm玻璃板上两个表面的测量位置Fig.11 Measured positions of the two surfaces of 2 mm glass plate

4 结束语

本文介绍了一种基于位相逆推法的多周期条纹投影干涉仪，并成功运用该种方法测量物体表面形状。在条纹周期的扫描中利用反馈技术使物体表面上一个点的位相保持在π/2。在位相逆推法中，对应于不同条纹周期的各测量点的振幅，位相值及相对固定位相点的空间位置构成一个逆推场，当逆推光场总和的振幅变为最大值且其位相变为0时，由逆推的距离可以得到物体表面的位置。由数值仿真及实验分析可以得到，当测量范围为毫米级时，基于多周期条纹投影法的位相逆推法测量精度可以达到微米级，并且基于多周期条纹投影技术的位相逆推法还可用于测量物体两个表面的形状。

［1］CREATH K，WYANT J.Moire and fringe projection Techniques in Optical Shop Testing［M］.New York:Wiley，1992:653－686.

［2］GREIVENKAMP J，BRUNING J.Phase Shifting Interferometers in Optical Shop Testing［M］.New York:Wiley，1992:653－686.

［3］TAKEDA M，INA H，KOBAYASHIS.Fourier－transform method of fringe－pattern analysis for computer－based topography and interferometry［J］.Opt Soc，1982(72):156－160.

［4］KUWAMURA S，YAMAGUCHI I.Wavelength scanning profilometry for real－time surface shapemeasurement［J］.Appl Opt，1997，36(19):4473－4482.

［5］WAGNER C，OSTER W，SEEBACHER S.Direct shape measurement by digital wavefront reconstruction and multi－wavelength contouring［J］.Opt Eng，2000，39(1):79－85.

［6］TIZIANIH，FRANZE B，HAIBLE P.Wavelength－shift speckle interferometry for absolute profilometry using a mode－hop free external cavity diode laser［J］.JModern Opt，1997，44(8):1485－1496.

［7］ZHAO H，CHEN W，YAN Y.Phase－unwrapping algorithm for the measurement of three－dimensional object shapes［J］.Appl Opt，1994，33(20):4497－4500.

［8］ZHANG H，LALOR M，BERTON D.Spatiotemporal phase unwrapping for the measurement of discontinuous objects in dynamic fringe－projection phase－shifting profilometry［J］.Appl Opt，1999，38(16):3534－3541.

［9］SASAKIO，OKAZAKIH.Sinusoidal phasemodulating interferometry for surface profile measurement［J］.Appl Opt，1986，25(18):3137－3140.

［10］LI Jin－huan，SASAKI Osami.Measurement of a crosssectional profile of a thread gauge using a sinusoidally vibrating interference pattern［J］.Appl Opt，2011，50(20):3470－3474.

［11］TAKAMASA S，SASAKIOsami.Rapid wavelength scanning based on acousto－optically tuned external－cavity laser diode［J］.Opt Com，2011，284(19):4615－4618.

［12］ROSENDAHLl Sara，HALLSTIG Emil，SJODAHL Mikael.Phase errors due to speckles in laser fringe projection［J］.Appl Opt，2010，49(11):2047－2053.

(编辑:田海江)