FDTD 全波分析缺陷地结构微带线的高效算法实现

兰 婧，杨 阳，2，戴婧怡

(1.南京航空航天大学电子信息工程学院，南京 210016;2.毫米波国家重点实验室，南京 210096)

0 引言

缺陷地结构(defected ground structure，DGS)［1］是由学者Park J I提出，通过在接地板上刻蚀缺陷的图形形成的，以改变接地板上的电流分布，从而实现滤波。DGS占用较小的电路面积，有利于实现高性能与小型化，由于其独特的性能逐渐成为微波电路设计领域中的研究热点。

在微波电路的实际计算中，时域有限差分法(finite－difference time－domain，FDTD)因其简单有效性而越来越受到重视，但传统的FDTD方法属于显式差分，计算时间步长上限受到Courant稳定性条件(Courant－Friedrich－Levy，CFL)［2－3］的限制，而太小的时间步长会导致计算量和内存需求的增大，进而影响计算效率。对于缺陷地结构来说，由于其包含有微细尺寸，传统FDTD方法仿真计算时间大大增加。近年来，时域交替隐式差分方法(alternating－direction implicit FDTD， ADI－FDTD)［4］、LOD－FDTD(locally one dimensionally FDTD)［5］和 CN－FDTD(Crank－Nicolson FDTD)［6］等隐式无条件稳定 FDTD方法相继被提出以克服稳定性条件的限制，但这些方法的共同点是计算复杂、效率较低，并且易产生较大的离散误差。

在隐式方法的基础上，提出了一种新的混合隐显式时域有限差分法(hybrid implicit－explicit FDTD，HIE－FDTD)［7］，相比前几种 FDTD 方法的变形，HIEFDTD方法介于隐式和显式差分方法之间，保持了一种弱稳定性，能取到比普通FDTD方法更大的时间步长，并且计算复杂度比ADI－FDTD等隐式方法低，有更高的计算效率，在保持和传统FDTD方法精度相同的情况下，能节省内存，并且比较适合在某个方向上具有细微结构的电磁问题计算。本文通过运用HIE－FDTD方法对其进行变换，针对该方法提出了其相应的边界吸收条件的处理方法并且加以应用。通过计算两款哑铃型DGS微带线(该DGS微带线中各带有一个比较窄的矩形连接槽)给出了结果证明。

1 HIE-FDTD算法推导

1.1 算法基本公式

文献［7－8］中的 HIE－FDTD 方法适用于在 y方向有微细尺寸的结构，但在一些结构如哑铃型DGS微带中，微细尺寸集中在传播方向，即z方向。于是，在各向同性均匀媒质区域，假设空间剖分最小步长在z方向，得出变换后新的三维HIE－FDTD差分方法基本矩阵形式为

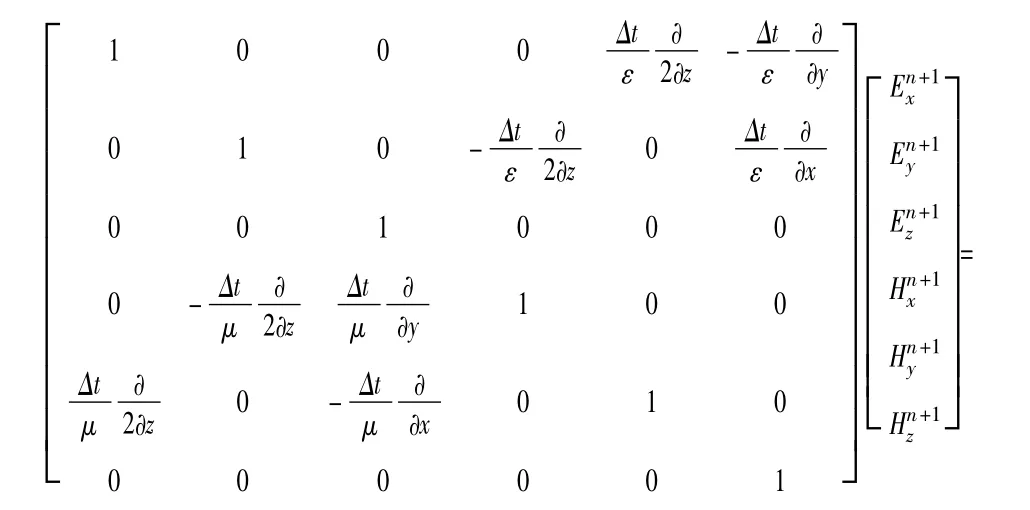
该HIE－FDTD方法需要求解2个隐式更新方程(隐式更新过程等价于对一个矩阵方程的求解，其中系数矩阵是一个带状三对角矩阵)，4个显式更新方程，计算复杂度远小于 ADI－FDTD［4］，CN－FDTD［6］方法的6个隐式更新方程、6个显式更新。提高了计算效率，节省了内存空间。

经变换的HIE－FDTD方法的稳定性条件［7］相应改为

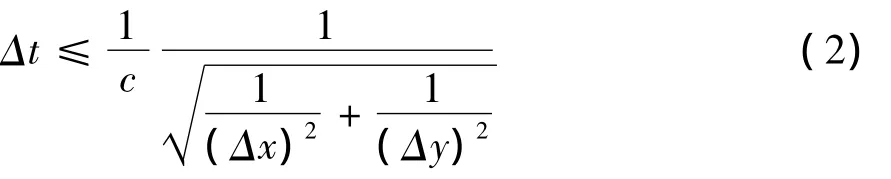
(2)式中:Δx，Δy分别为对应方向上的空间增量。

由(2)式可以看出，HIE－FDTD方法的时间步长只与2个方向的空间离散有关，如果计算模型在z方向上具有细微的结构，普通FDTD方法可取的时间步长将会非常小，使得普通FDTD方法难以实现，而HIE－FDTD方法却不会受到影响，并且HIE－FDTD方法也会因此减少计算时间。

1.2 吸收边界条件的处理

因为FDTD方法实际求解过程必须限定在一个有限的空间区域，所以，必须采用适当的吸收边界条件来模拟电磁波传播过程。Mur吸收边界条件［9－10］作为一种简单有效的差分数值算法，相比其他吸收边界条件节省占用内存，在FDTD方法中得到了广泛应用，因此，在对缺陷地结构做分析时我们采用Mur吸收边界条件，但并不同于其在传统FDTD方法中边界条件的使用方法。通常在使用Mur吸收边界条件时，尽量采用Mur二阶近似吸收边界条件，角点作一阶近似处理。具体公式参照文献［9］，而在HIE－FDTD方法中，由于需要求解复杂的三对角矩阵系统，不同于普通FDTD方法直接求解，场值的截断边界吸收条件需要分情况讨论。以Ex为例，关于Ex的求解可写成矩阵形式为(3)式中，A为三对角矩阵，由于三对角矩阵求解的特殊性，其首、末行元素只能用一阶Mur吸收边界条件得到。

至于不涉及三对角矩阵求解的Ez节点，以x=0边界为例，吸收边界条件仍然按照一般方法，即在截断边界上与棱边相邻的节点采用Mur一阶近似吸收边界条件，如(6)式，而其他节点都用Mur二阶近似吸收边界条件，如(7)式。

2 DGS全波分析实例

2.1 典型DGS微带线的分析计算

我们用经过变换的HIE－FDTD方法对典型DGS微带线进行时域和频域上的仿真分析，传统FDTD方法仿真结果与其结果进行了比较。典型DGS微带线(见图1)［1］由2个同样大小的大矩形槽和一个较窄的矩形连接槽构成，外形酷似哑铃，结构中基片介质参数εr=2.2，厚度h=0.787 4mm。计算空间为16×29 ×200，取Δx=0.787 4 mm，Δy=0.5 mm，Δz=0.1 mm。激励源为高斯脉冲，在微带线输入和输出端口设置两个参考面，得到其电场值Ez的时域波形。

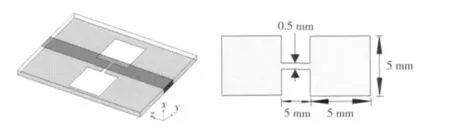
图1 哑铃型DGS微带线结构图Fig.1 Configuration of the dumb－bell shaped microstrip DGS

传统FDTD方法能满足的最大的时间步长Δt由 Courant条件［2］可得

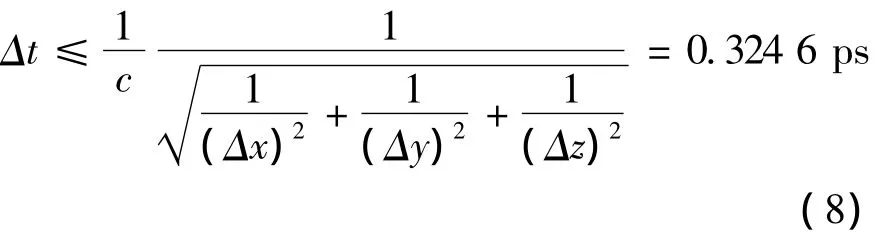
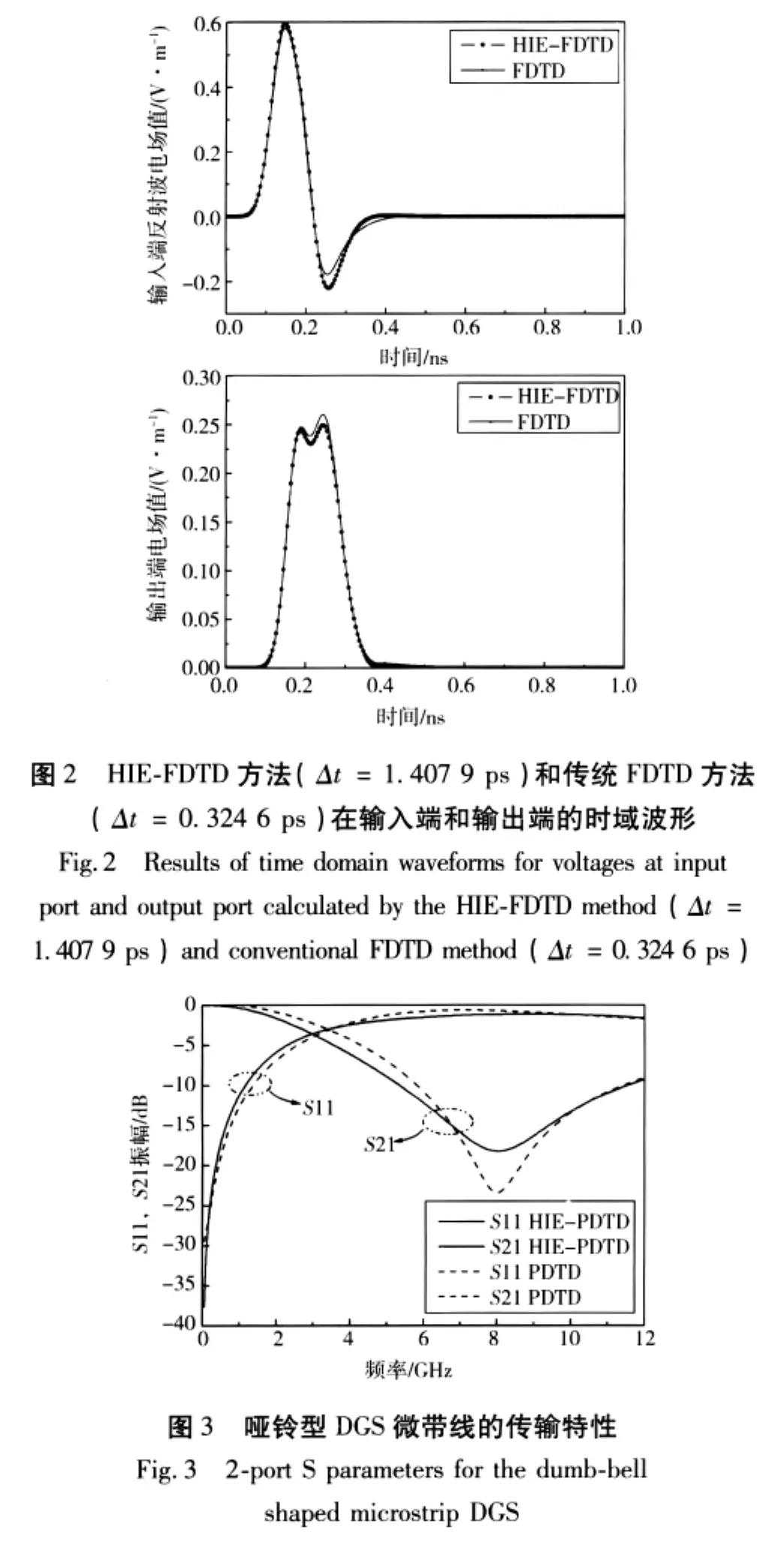
在HIE－FDTD方法中，由(2)式确定数值解稳定的条件为Δt≤1.407 9 ps。图2为HIE－FDTD方法和传统FDTD方法分别在输入和输出端得到的电场时域波形。可以看出，在时间步长取值比传统FDTD方法大的情况下，HIE－FDTD方法的结果和传统FDTD方法结果基本吻合。

接下来对时域数据离散快速傅立叶变换(fast Fourier transform，FFT)得到该DGS微带线的宽频带响应计算得出其S参数幅值图如图3所示。频率为0～12 GHz，HIE－FDTD方法计算的S参数与传统FDTD方法结果相近。

HIE－FDTD方法和传统FDTD方法在该计算过程中所用的计算时间如表1所示。由表1得出，因为HIE－FDTD方法计算过程比传统 FDTD方法复杂，在相同情况下，HIE－FDTD方法的计算时间要比传统FDTD方法大，但由于其弱稳定性能取到比传统FDTD方法要大的时间步长，仍能节省计算时间。

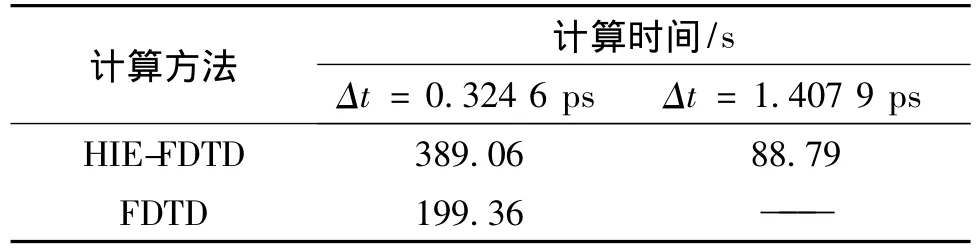
表1 计算过程中所用的计算时间Tab.1 CPU times for the simulations

2.2 Slanted哑铃型DGS微带线的分析计算

Slanted哑铃型DGS微带线结构如图4所示［11］，与典型DGS微带线一样由2个大矩形槽和一个较窄的矩形连接槽构成，但是2个大矩形槽沿窄带矩形槽左右对称，该DGS微带线可用于普通DGS微带线不适用的平行耦合线滤波器中，具有很好的滤波特性。基片介质参数εr=4.4，损耗因数tanδ=0.02，厚度h=1.5 mm。微带线宽度为w=3.09 mm，计算空间为32×23×295，取Δx=1.5 mm，Δy=1mm，同时因传播方向有纤细结构取Δz=0.1 mm。激励源为调制高斯脉冲。

图4 Slanted哑铃型DGS微带线结构图Fig.4 Configuration of the slanted dumb－bell shaped microstrip DGS

传统FDTD方法能满足的最大的时间步长Δt由Courant条件可得Δt≤0.331 2 ps。

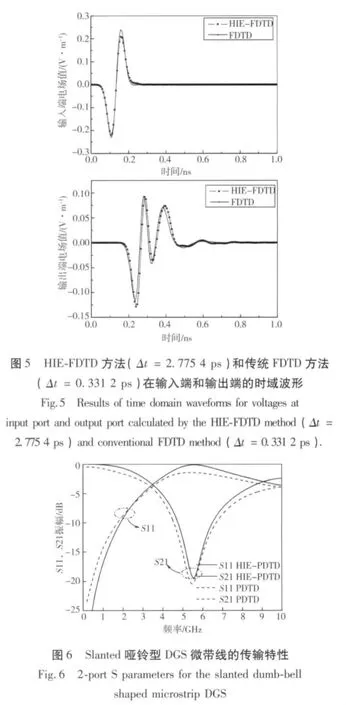
在HIE－FDTD方法中，由(2)式确定数值解稳定的条件为Δt≤2.775 4 ps。图5为HIE－FDTD方法和传统FDTD方法在输入和输出端得到的电场时域波形。该DGS微带线的S参数幅值图如图6所示。图6中，频率为0～10 GHz，HIE－FDTD方法计算的S参数都与传统FDTD方法非常接近。

HIE－FDTD方法和传统FDTD方法在该计算过程中所用的计算时间如表2所示。

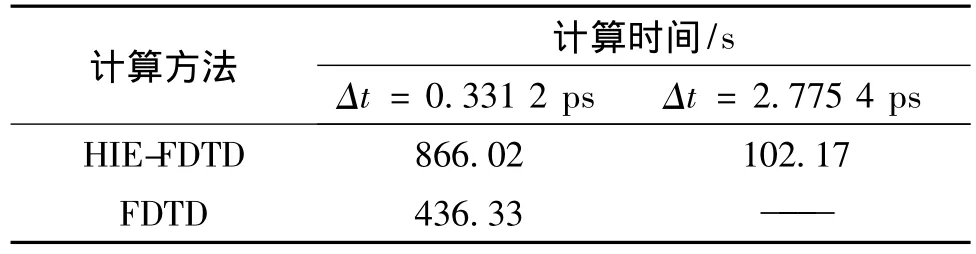
表2 计算过程中所用的计算时间Tab.2 CPU times for the simulations

从HIE－FDTD方法相关文献的计算结果看，在文献［7－8］中，其给出的 HIE－FDTD 方法的时域计算结果与传统FDTD方法的计算结果符合得很好，而在文献［12－13］中，HIE－FDTD 方法的时域、频域计算结果与传统FDTD方法的计算结果相比均有偏差，这和计算结构是否为二维、三维结构，是否需要考虑吸收边界有关，因为Mur边界在HIE－FDTD方法中的使用不能达到在普通FDTD方法相同的精度。

从文中HIE－FDTD方法和传统FDTD方法对2款DGS微带的时域和频域的计算结果看，HIEFDTD方法与传统FDTD方法的一致程度较高，并能显著减少计算时间，同时HIE－FDTD方法的吸收边界条件性能良好。

3 结论

本文将一种经变换后的弱稳定性条件的HIEFDTD方法应用于2款DGS微带线的电磁特性分析，还详细分析了吸收边界条件在HIE－FDTD方法中的应用研究。数值结果表明，HIE－FDTD方法不仅保持了和传统FDTD方法相近的精度，计算时间能减少到传统FDTD的1/2～1/4，并且提出的吸收边界条件的处理保证了吸收边界的稳定性，收敛效果良好。因其数值稳定条件在三维空间中只取决于2个方向，这种弱条件稳定性使得HIE－FDTD方法在保持精度的基础上，提高了DGS的仿真效率，该方法特别适用于DGS微带线以及其他在传播方向上具有微细结构的微带平面电路的电磁数值分析。

［1］PARK J I，KIM C S，KIM J，et al.Modeling of a photonic bandgap and its application for the low－pass filter design ［C］//1999 Asia－Pacific Microwave Conf Dig，［s.l.］:IEEE Press，1999，2:331－334.

［2］TAFLOVE A，HAQNESSSC.Computational Electromagnetics:The finite－difference time－domain method ［M］.Boston，MA:Artech House，2000.

［3］童创明.计算电磁学快速方法［M］.西安:西北工业大学出版社.2010.

TONG Chuang－ming.Fastmethod for computational electromagnetics［M］.Xi'an:Northwest Polytechnic University Press，2010.

［4］FUW M，TAN E L.Stability and Dispersion Analysis for ADI－FDTD Method in Lossy Media［J］.IEEE Trans Antennas and Propagat，2007，55(4):1095－1102.

［5］AHMED I，CHUA E K，LI E P，et al.Numerical dispersion analysis of the unconditionally stable three－dimensional LOD－FDTD method ［J］.IEEE Trans Antennas and Propagat，2010，58(12):3983－3989.

［6］YANG Y，FAN Z H，DING D Z，et al.Extend two－step preconditioning technique for the Crank－Nicolson finitedifference time－domainmethod to analyze the 3D microwave circuits［J］.International Journal of RF and Microwave Computer－Aided Engineering，2009，19(4):460－469.

［7］CHEN J，WANG J.A 3－D hybrid implicit－explicit FDTD schemewith weakly conditional stability［J］.Microw Opt Tech Lett，2006，48(11):2291－2294.

［8］CHEN J，WANG J.Comparison between HIE－FDTD method and ADI－FDTD method［J］.Microw Opt Techno Lett，2007，49(5):1001－1005.

［9］MUR G.Absorbing boundary conditions for the finitedifference approximation of the time－domain electromagnetic field equations［J］.IEEE Trans Electromagn Compat，1981，EMC－23(4):377－382.

［10］WEIC T，TAN E L.Mur absorbing boundary condition for efficient fundamental3－D LOD－FDTD ［J］.IEEE Microwave and Wireless Components Letters，2010，20(2):61－63.

［11］KARSHENASF，MALLAHZADEH A R，RASHED－MOHASSEL J.et al.Size reduction and harmonic suppression of parallel coupled－line bandpass filters using defected ground structure［C］//2009 13th International Symposium on Antenna Technology and Applied Electromagnetics and the Canadian Radio Sciences Meeting，Toronto，ON:IEEE Press，2009:1－6.

［12］HUANG B K，WANG G，JIANG Y S，et al.A Hybrid Implicit－Explicit FDTD scheme with weakly conditional stability［J］.Microw Opt Tech Lett，2003，39(2):97－101.

［13］AHMED I，LIEP.Convolutional perfectlymatched layer for weakly conditionally stable hybrid implicit and explicit－FDTDmethod ［J］.IMicrow Opt Tech Lett，2007，49(12):3106－3109.

(编辑:魏琴芳)