盲孔法测定径向锻造身管表面残余应力方法研究

刘力力，樊黎霞，董雪花

(1.南京理工大学 机械工程学院，江苏 南京210094;2.南京理工大学 理学院，江苏 南京210094)

由于径向锻造工艺的特点，锻后身管表面存在轴向和周向的残余应力，残余应力的存在会对身管的强度、刚度、稳定性及抗疲劳等性能产生影响，因此，有必要测定锻造后身管表面的残余应力分布，准确评价其对使用性能的影响。

盲孔法在1934年由德国学者Mathar［1］提出，现已发展成为一种较成熟的测定残余应力的方法。近年来国内外学者对影响盲孔法测量精度的各因素进行了深入的研究:文献［2］对孔位、孔径、孔深对测量精度造成的影响做了详细研究;文献［3］确定了不影响测量精度的最小的边界值及孔间距;文献［4］详细分析了由于钻削附加应变所引起的误差;文献［5－6］分别介绍了误差迭代计算修正法及A、B 系数分级使用修正法修正由孔边塑性变形所致的误差;近年随着有限元法的发展，许多学者开始应用有限元法确定盲孔法中的应变释放系数，文献［7－8］是用有限元数值模拟应变释放系数的测试试验，并通过基于孔边形状改变比能修正应变释放系数，以消除孔边塑性变形的影响。

国内外学者虽已对盲孔法进行了大量深入的研究，但主要都是以平板表面残余应力为例，只有少数以圆管为例，如文献［9］对用盲孔法测定圆钢管表面残余应力时的释放系数进行了一些研究。本文从测定径向锻造身管表面残余应力的实际需要出发，将盲孔法测定平板表面残余应力的理论应用到径向锻造身管表面残余应力的测量中。由于有限元法模拟应变释放系数的准确性已得到很多学者的验证，因此首先应用有限元软件ABAQUS 计算相同材料、受力情况及钻孔条件下不同外径身管表面盲孔的释放系数与平板表面盲孔的释放系数，通过释放系数差值的对比，得到盲孔法测量径向锻造身管表面残余应力的适用性范围。钻孔偏心是影响盲孔法测量精度的主要因素，已有的修正由钻孔偏心所致误差的方法都是通过对盲孔周围的受力分析，并要通过循环迭代得到最终的结果，如文献［10－11］，此方法受力分析过程复杂，且循环迭代不易收敛，本文结合有限元法测定应变释放系数准确方便的特点，提出了一种通过直接修正应变释放系数来修正由钻孔偏心所引起的误差的新方法。应用盲孔法测定某具体锻后身管表面的残余应力，根据身管的形状特点，忽略可能存在的孔边塑性变形及其它因素对测量结果的影响，只通过直接修正应变释放系数来修正由钻孔偏心所引起的误差。

1 盲孔法测量的基本原理

若主应力方向上板的残余应力为σ1、σ2(大小、方向未知)，在板上贴一(0° 90° 225°)应变花(使0°方向的应变片水平)，并在应变花中心钻一直径为a、深度为h 的小盲孔，如图1所示。

由于钻孔使孔周围部分的应力松弛而引起残余应力的变化，形成新的应力场和应变场。由钻孔而分别在3 个应变片上产生的应变与板上残余主应力有如下的关系［12］:

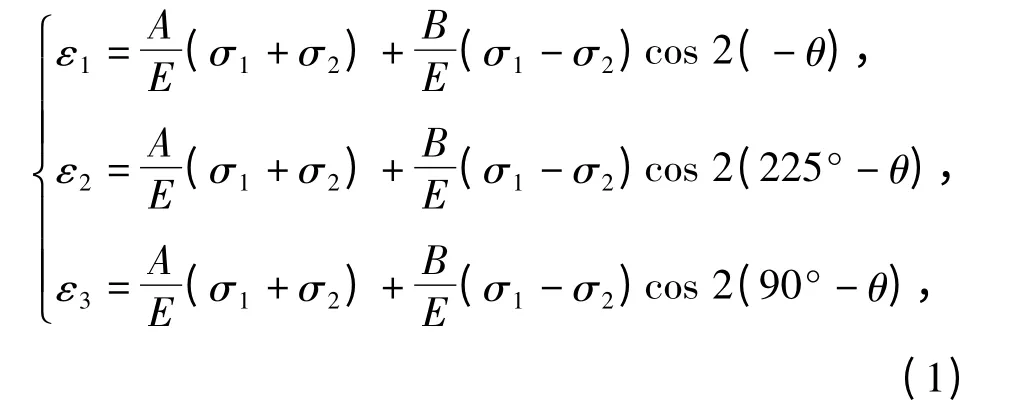
图1 盲孔法测量原理图Fig.1 Measurement principle of blind－hole method

式中:ε1、ε2和ε3分别为由应变片R1、R2和R3所测得的释放应变;A、B 为应变释放系数;σ1、σ2为残余主应力;θ 为应变片R1与残余主应力σ1间夹角;E为材料弹性模量。

为求解(1)式中的σ1，σ2与θ，需确定应变释放系数A，B.通孔的应变释放系数由公式计算得出，盲孔的应变释放系数通常由单向应力标定试验测定，近年来，用有限元法标定盲孔的应变释放系数的准确性及优越性已得到验证。

有限元法标定应变释放系数的原理图如图2所示，在板上施加确定的主应力σ1，σ2，用有限元模拟被测构件钻孔前后的受力状态，在距钻孔中心半径为r 的圆周上取与主应力σ1夹角分别为θi，θj的两点i，j，确定钻孔前后两点径向的应变值。则i，j 两点钻孔后的应变释放值与主应力σ1、σ2的关系式为

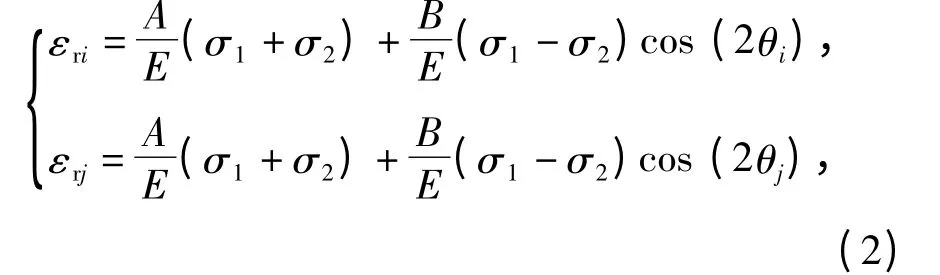
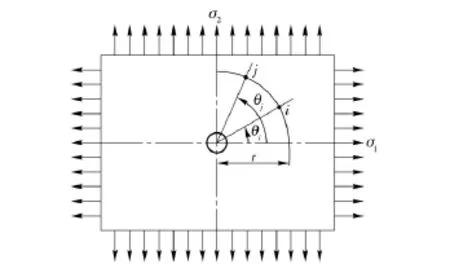
图2 有限元标定释放系数原理图Fig.2 Principle of calibration for relaxation coefficient

式中:εri，εrj分别为i，j 两点钻孔后径向的应变释放值，大小为钻孔后每点的径向应变与钻孔前每点的径向应变的差值。

求解(2)式中的方程组，即可求得应变释放系数A，B.

2 盲孔法测定径向锻造身管表面残余应力的有限元方法研究

2.1 盲孔法测定径向锻造身管表面残余应力的适用性范围

用盲孔法测定径向锻造身管表面的残余应力，主要是将一定范围内的径向锻造身管表面视为平面，因此对于不同外径的身管，在其表面钻孔后，只有在一定范围的表面内才可应用由平板理论推导出的(1)式，为得到盲孔法对于径向锻造身管的可应用范围，采用上节所述有限元法标定应变释放系数的方法，用ABAQUS 有限元软件建立不同外径身管的有限元模型，取无量纲参量D/a:身管外径D 与钻孔直径a 的比值，表征不同外径的径向锻造身管。分别取D/a=9，D/a =12、D/a =16 和D/a =20 的身管作为研究对象。材料性能:E=2.07 ×105MPa，泊松比υ=0.3，屈服强度σs=940 MPa;为保证钻孔后的材料仍处于弹性变形，而受单向力作用的孔边应力集中系数为3，所以模拟时施加的力需小于材料屈服强度的1/3，此模拟中，轴向施加200 MPa 的压力。作为对比参照，建立相同材料性能、受力情况与钻孔条件下的平板有限元模型。分别模拟身管和平板有孔与无孔的受力状态。身管和平板有孔与无孔的有限元模型如图3和图4所示。

图3 身管有限元模型局部视图Fig.3 Partial view of finite element model of gun barrel

取无量纲参量r/a:距钻孔中心距离r 与钻孔直径a 的比值，表征距钻孔中心的不同位置。由(2)式分别计算对应在不同D/a 的径向锻造身管上，不同r/a 值的圆周上的应变释放系数A，B，为得到更精确的A，B 值，在同一半径的圆周上取与受力方向夹角为0°，22.5°，45°，67.5°和90°的5 个测点(模型具有对称性，只取1/4 圆周上的点)，可求得C25 个A，B 值，求其算术平均值即为A，B 值。所求得的当D/a=9，D/a =12、D/a =16 和D/a =20 时的径向锻造身管上不同r/a 值圆周上的应变释放系数A，B值与相应平板上r/a 值圆周上的应变释放系数A，B值的误差值如图5～图8所示。

图4 平板有限元模型局部视图Fig.4 Partial view of finite element model of plate

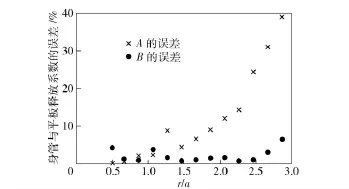
图5 D/a=9 时身管与平板释放系数A、B 的误差Fig.5 Errors between barrel and plate relaxation coefficients when D/a=9

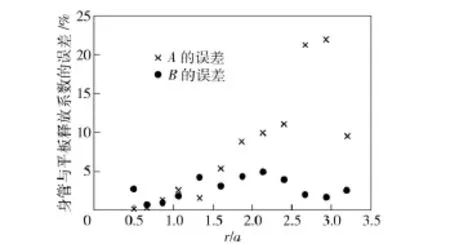
图6 D/a=12 时身管与平板释放系数A、B 的误差Fig.6 Errors between barrel and plate relaxation coefficients when D/a=12

当身管与平板的释放系数A 或B 的误差达到5%时，会对残余应力的计算结果产生影响。由图5～图8可知，当D/a =9，r/a =1.27 时，身管与平板的释放系数A 的误差最先超过5%，达到8.8%;当D/a=12，r/a=1.6 时，身管与平板的释放系数A 的误差最先超过5%，达到5.3%;当D/a =16，r/a=2.8 时，身管与平板的释放系数B 的误差最先超过5%，达到5.6%;当D/a =20，r/a =3.33时，身管与平板的释放系数B 的误差最先超过5%，达到5.5%.对于不同的D/a，当释放系数A 或B 的误差最先超过5%时所对应的r/a 的值如图9所示。

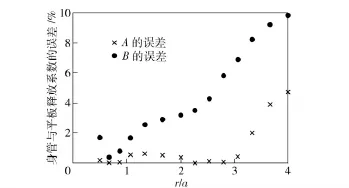
图7 D/a=16 时身管与平板释放系数A、B 的误差Fig.7 Errors between barrel and plate relaxation coefficients when D/a=16

图8 D/a=20 时身管与平板释放系数A、B 的误差Fig.8 Errors between barrel and plate relaxation coefficients when D/a=20

从图9中可知，随着D/a 的增大，r/a 也随之增大。对于盲孔法，钻孔直径及所选应变花通常都是固定的，应变片的外边缘处所对应的r/a 值通常小于2.5，从图9中可知，当D/a≥16 时，身管上应变花粘贴范围内的应变释放系数A，B 与平板应变释放系数A，B 的误差不超过5%，即可应用盲孔法测定其表面的残余应力。

图9 误差超过5%时，D/a 与r/a 的对应关系Fig.9 Relationship between D/a and r/a for error more than 5%

2.2 钻孔偏心修正法

文献［10］表明只有钻孔偏心的距离在0.025 4 mm 范围内时，才可忽略其对结果的影响，大多数钻孔设备都难以保证此精度。实际钻孔中心与所贴应变花的位置关系示意图，如图10 所示。图10 中:O点为应变花中心;P 点为钻孔中心;用线段OP 的长度s 及OP 与0°方向应变片的夹角β 表征钻孔偏心的位置;r1，r2，r3分别为钻孔中心与3 个应变片中心之间的距离。

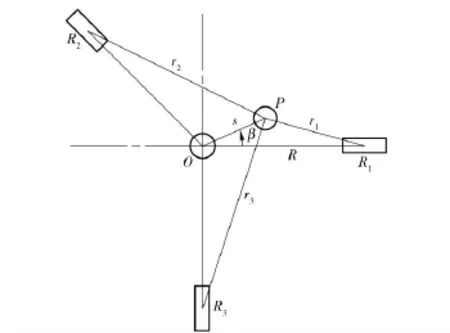
图10 钻孔与应变花的位置关系示意图Fig.10 Position relationship between drilling hole and strain gage

将应变片所测应变值看作应变片中心处的应变值，当钻孔中心与应变花中心重合时，即r1，r2，r3相等时，对于(1)式中的3 个方程，3 个应变片中心处的应变释放系数是相同的，当存在钻孔偏心时，即r1，r2，r3不相等时，3 个应变片中心处对应的应变释放系数分别为A1、B1;A2、B2;A3、B3.忽略钻孔偏心所引起的钻孔与应变片之间夹角的变化，仍采用应变花中心与应变片之间的夹角关系，只用钻孔偏心所引起的各应变片中心处应变释放系数的变化来修正钻孔偏心对结果的影响。则对应图10 所示的钻孔偏心与应变花的位置关系，(1)式变形为

求解(3)式方程组，即可求得钻孔处的主应力σ1、σ2及夹角θ.

3 试验应用

3.1 试验概况

将盲孔法测定径向锻造身管表面残余应力的方法应用到某具体锻后身管表面残余应力的测量中，身管尺寸参数:内径d =5.56 mm，D =24 mm;材料参数:E=2.07 ×105MPa，υ =0.3，σs=940 MPa;钻孔参数:a=1.5 mm，h=2 mm;则对应第2.1 节中所取的无量纲参量D/a =16，所贴应变花为一(0°－90°－225°)应变花，使0°方向与身管轴线平行，应变花外边缘处距应变花中心处的距离与钻孔直径的比值r/a=2.3，由2.1 节中所得结论知，可应用盲孔法测定此锻后身管表面的残余应力。钻孔后的试样如图11 所示。3 个应变片上所测得的应变值如表1所示。

图11 钻孔后的试样Fig.11 Sample of gun barrel after drilling

表1 应变片所测应变值Tab.1 Measured strain

3.2 钻孔偏心的修正及试验结果

对照图10，试验中所贴应变花的应变花中心到应变片中点的距离R =2.565 mm;钻孔偏心对应的s=0.571 2 mm;β =29.9°，由此计算出r1，r2，r3如表2所示。

表2 计算所得r1，r2，r3值Tab.2 Calculated r1，r2 and r3

应用2.1 节中所述有限元法计算应变释放系数的方法，计算对应此锻后身管的尺寸、材料参数及钻孔条件下的距钻孔中心不同点处的应变释放系数A、B 值，用MATLAB 软件对身管不同距离圆周上的应变释放系数A、B 值进行多项式拟合，得到A、B 值关于测点与孔中心距离r 的函数关系式为

将表2中的值分别代入(4)式，得到对应试验中实际的钻孔中心，3 个应变片中心处的应变释放系数A，B 值，具体结果如表3所示。

表3 应变片中心处的释放系数值Tab.3 Relaxation coefficients on gage’s center

将表1、表3中的具体数值及E 的数值代入(3)式，并求解(3)式的方程组，得到锻后身管表面残余主应力σ1、σ2及夹角θ 的值，将主应力分解到身管的轴向与周向上，即可得到锻后身管表面轴向σr与周向的残余应力σθ.具体结果如表4所示。

表4 身管表面各残余应力Tab.4 Residual stresses on barrel surface

4 结论

本文应用ABAQUS 有限元软件数值标定盲孔法的释放系数A，B 值，通过对比在相同条件下径向锻造身管表面与平板表面的释放系数值，得到盲孔法测量径向锻造身管表面残余应力的适用性范围;提出一种通过直接修正释放系数值的方法来修正钻孔偏心所引起的误差;并将此方法应用到某具体锻后身管表面残余应力的测量中。得到以下结论与建议:

1)随着身管外径与钻孔直径的比值D/a 的增大，身管与平板的释放系数的误差不超过5%的所对应的最大的r/a 值也随之增大。

2)对于盲孔法通常所选用的钻孔直径和应变花尺寸，当D/a≥16 时，在应变花粘贴范围内(应变片的外边缘处所对应的r/a 值通常小于2.5)，身管释放系数与平板释放系数的误差不超过5%，即可应用盲孔法测定其表面残余应力。

3)可通过直接修正释放系数值来修正钻孔偏心所引起的误差，此方法与有限元法结合，准确方便。

4)锻后身管表面存在轴向684 MPa 的残余压应力;周向680 MPa 的残余压应力。锻造后身管表面存在如此大的残余应力，将会对身管的使用性能有很大的影响。

References)

［1］ Mathar J.Determination of initial stresses by measuring the deformation around drilled holes［J］.Trans ASME，1934，56:245－254.

［2］ Bynum J E.Modifications to the hole－drilling technique of measuring residual stresses for improved accuracy and reproducibility［J］.Experimental Mechanics，1981，21(1):21－30.

［3］ 裴怡，包亚峰，唐慕尧，等.盲孔法测量精度的研究—边界及孔间距的影响［J］.焊接学报，1994，15(3):191－196.PEI Yi，BAO Ya－feng，TANG Mu－yao，et al.Effect of boundary and distance between holes on accuracy of blind hole technique［J］.Trans of the China Welding Institution，1994，15(3):191－196.(in Chinese)

［4］ Flaman M T.Brief investigation of induced drilling stresses in the center－hole method of residual－stress measurement［J］.Experimental Mechanics，1982，22(2):26－30.

［5］ 刘伯梁，焦建强，李广铎.钻孔法测定焊接残余应力时的εp［J］.实验力学，1994，9(2):115－123.LIU Bo－liang，JIAO Jian－qiang，LI Guang－duo.Effect of released plastic strain in determining residual welding stress by hole－drilling method［J］.Journal of Experimental Mechanics，1994，9(2):115－123.(in Chinese)

［6］ 黄蓝林，唐慕尧，孟繁森.焊接应力测量中A、B 系数分级应用的研究［C］∥第六届全国焊接学术会议论文选集.西安:西安交通大学出版社，1991:4－25.HUANG Lan－lin，TANG Mu－yao，MENG Fan－sen.The study of the classification application for the A、B coefficients in the measurement of welding stress［C］∥The Sixth National Conference of Welding.Xi’an:Xi’an Jiaotong University Press，1991:4－25.(in Chinese)

［7］ 谭明鹤，王荣辉，黄永辉.盲孔法测残余应力中应变释放系数的修正方法［J］.热加工工艺，2007，36(19):65－68.TAN Ming－he，WANG Rong－hui，HUANG Yong－hui.Correctional method of strain release coefficients by blind－hole technique to measure residual stress［J］.Hot Working Technology，2007，36(19):65－68.(in Chinese)

［8］ 刘晓红，苏文桂，张运泉.屈服状态下盲孔法测量残余应力孔边应变释放系数修正［J］.铸造技术，2010，31(1):36－39.LIU Xiao－hong，SU Wen－gui，ZHANG Yun－quan.Strain releasing factor amendment of hole edge under the yield Status［J］.Foundry Technology，2010，31(1):36－39.(in Chinese)

［9］ 王龙.盲孔法测量圆钢管表面应力的试验与分析［J］.建筑科学，2009，25(9):48－52.WANG Long.Experimental study and analysis of stress measurement of circular steel tubes by using blind－hole method［J］.Building Science，2009，25(9):48－52.(in Chinese)

［10］ Sandifer J P，Bowie G E.Residual stress by blind－hole method with off－center hole［J］.Experimental Mechanics，1978，18(5):173－179.

［11］ Wang H P.The alignment error of the hole－drilling method［J］.Experimental Mechanics，1979，19(1):23－27.

［12］ 陆才善.残余应力测试—小孔释放法［M］.西安:西安交通大学出版社，1991:10－24.LU Cai－shan.The measurement of the residual stresses［M］.Xi'an:Xi'an Jiaotong University Press，1991:10－24.(in Chinese)