基于双谱熵模型的故障模式识别

黄晋英，潘宏侠，毕世华，崔宝珍

(1.中北大学 机械工程与自动化学院，山西 太原030051;2.北京理工大学 宇航学院，北京100081)

近年来，信息熵作为故障模式识别的特征参量越来越得到工程界的重视［1］。信号的信息熵［2］是指信号中所含的平均信息量，随着先验概率的增加而减少，但却随着后验概率的增加而增加，反映了信号中所含信息的复杂程度。齿轮箱的振动信号在结构特性一定时，其信息熵维持在一定水平，当结构发生故障时，测试信号所含信息的复杂程度发生变化，其信息熵也发生变化，不同故障模式下，信息熵的值不同，采用信息熵可以实现对设备运行状态特征的描述和评价，区分故障。研究者将信息熵思想和不同信号分析方法相结合，建立了多种信息熵特征指标用于工程信号分析和系统状态监测与故障诊断［3］，如功率谱熵、小波能量谱熵［4］、奇异谱熵［5］、希尔伯特－黄变换熵［6］、EMD 时频熵［7］、关联距离熵、renyi 熵［8］等。本文提出的双谱熵模型，是在双谱域内建立的信息熵特征参量。

在研究信息熵理论的基础上，建立了振动信号的双谱熵模型，并针对实验室齿轮箱的4 种典型故障状态，对其振动信号进行了双谱分析，计算了双谱熵特征参量，建立BP 神经网络模型进行了故障模式识别，识别结果表明，利用双谱熵特征参量进行故障模式识别，在测点数量少的情况下能获得较高的诊断精度。

1 双谱熵模型的建立

1.1 双谱

设随机过程{x(n)}在任意n，n + m1，…，n +mk－1时刻的k 维随机矢量

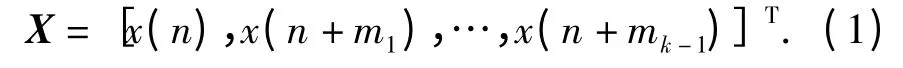
则三阶累积量为

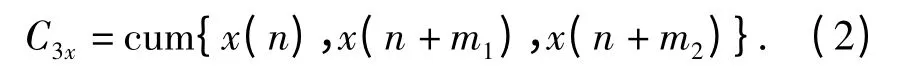
三阶累积量的Fourier 变换，即为信号的双谱。若三阶累积量C3x(m1，m2)绝对可和，即

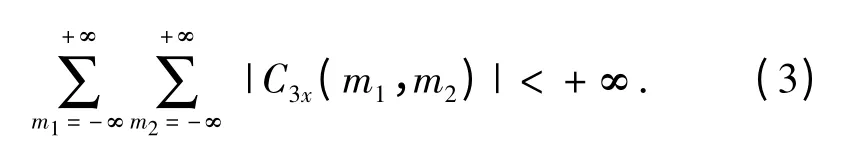
则双谱表示为［9－10］

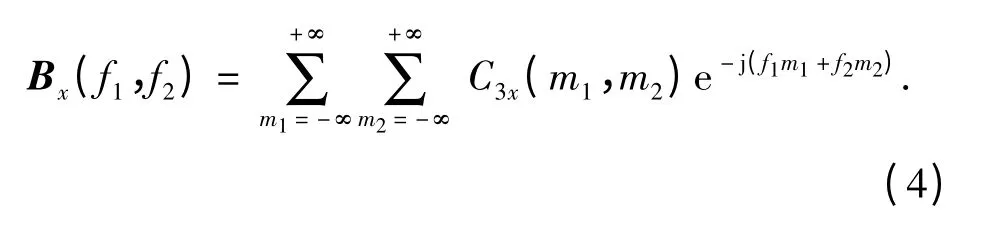
双谱为对称矩阵，是双周期函数，其周期为2π，三维图形通常呈“钉床”形［11］。

1.2 信号的信息熵

信息熵理论研究信息的定量描述方法，从平均意义上表征信号总体信息测度，计算公式如下:

式中:X={x1，x2，…，xn}为离散信号，从广义的角度来讲，可以是任意域的信号，其幅值出现的概率Pi=P(xi)，i=1，2，…，n，且

1.3 齿轮箱振动信号双谱熵模型的建立

测试得到的振动信号幅值通常在一定范围内连续分布，不可能按照幅值点一一计算概率，因此，基于信号能量在某分析域子空间的分布概率来建立信息熵。

1.3.1 子空间分布概率［12］

设S 为随机信号X 的特征空间，S1，S2，…，SN是其正交特征子空间，是S 的一个完全划分，则:

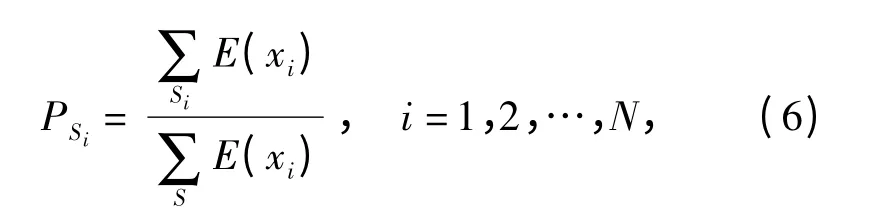
为信号X 在正交特征划分子空间SN下的子空间分布概率。式中:E(·)为能量函数;N 为子空间的个数。显然，PSi表征的是特征子空间Si能量所占整个信号特征空间能量的比例。

1.3.2 子空间分布概率概念下的信息熵

根据信息熵理论，可得到子空间分布概率概念下的信息熵

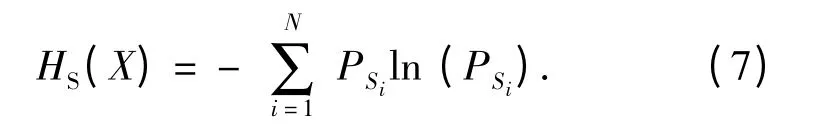
上述表征的是信号能量在各特征子空间之间分配的均匀程度，如果信号在某一特征子空间出现突变，其相应的子空间概率也会发生变化，从而导致信息熵变化。当各子空间能量相等时，信息熵HS(X)=ln N，因此HS(X)∈(0，ln N)，将(7)式标准化得

1.3.3 双谱熵计算模型

由时域信号计算得到的双谱是双频率的三维矩阵，在进行子空间划分时要考虑两维频率的划分，即将f1轴划分为N1组，将f2轴划分为N2组，此时划分出的总特征子空间数为N1N2，各子空间若用Sij来表示，则各特征子空间在S 下的子空间概率可表示为

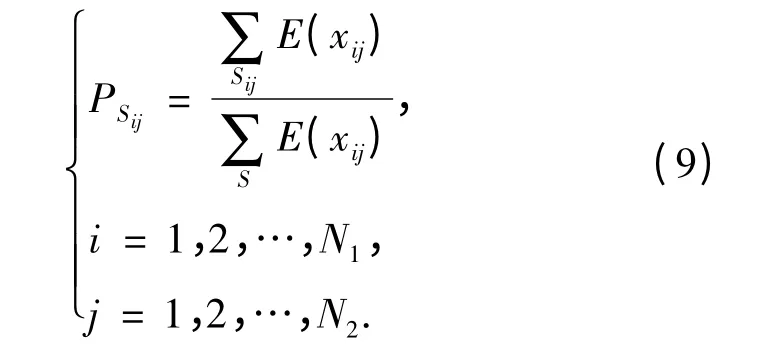
双谱熵可表示为

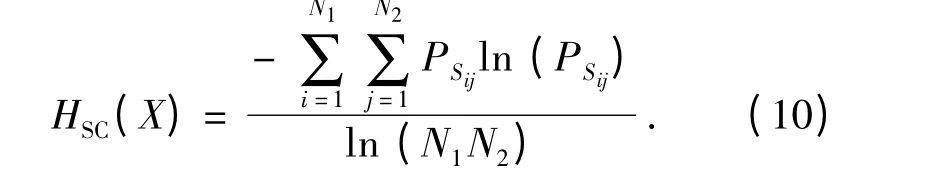
2 齿轮箱故障模式识别实验

实验对象为JZQ250 二级传动减速器，传动比10.35，共有2 对斜齿轮和6 个滚动轴承，其传动简图如图1所示。

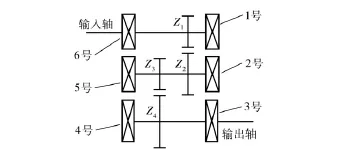
图1 齿轮箱传动简图Fig.1 Transmission of gearbox

输入轴齿轮Z1齿数为30;中间轴齿轮Z2和Z1啮合，齿数为69;Z3与输出轴齿轮Z4啮合，齿数分别为18 和81;1、2、5、6 号轴承型号相同，滚子数为6;3 号和4 号轴承滚子数为8.振动信号通过安装在减速器箱体上轴承座处的6 个压电式加速度传感器获得的，实验设置4 种工况:正常、Z2断齿、中间轴2号轴承外圈和内圈点蚀故障。通过变频器调节齿轮箱输入轴转速设置为900、1 200 和1 500 r/min，工作过程中利用抱闸给系统加小负载。输入轴转速为1 200 r/min 时，齿轮箱各特征频率如表1所示。

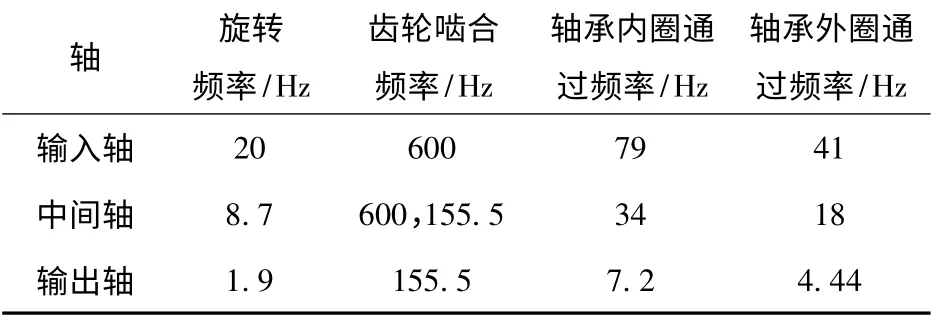
表1 齿轮箱特征频率Tab.1 Characteristic frequency of gearbox

2.1 双谱分析

图2～图5为1 200 r/min 时测点4 振动信号的双谱三维瀑布图。从双谱图上看，正常工况下仅在转频处出现最大峰值;断齿故障除在转频附近出现峰值带外，还出现了频率耦合现象，耦合频率约为(45，150)和(150，45)，是转频的倍频调制齿轮啮合频率的结果。两种轴承故障的双谱分布差异比较明显，内圈故障的特征峰值比较丰富，主要分布在300 Hz 以内，300 Hz 外也存在较明显的峰值，而外圈故障频带仅分布在300 Hz 以内。信号的双谱可以明显区分上述4 种工况。

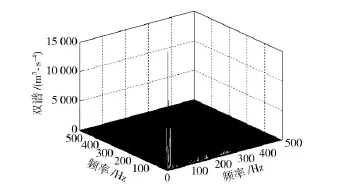
图2 正常工况双谱瀑布图Fig.2 Bispectrum waterfall in normal state

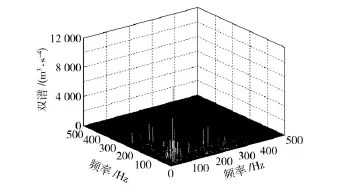
图3 断齿故障双谱瀑布图Fig.3 Bispectrum waterfall of gear fault

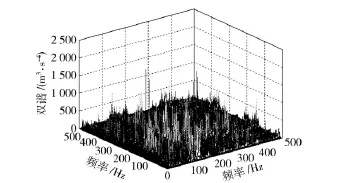
图4 轴承内圈故障双谱瀑布图Fig.4 Bispectrum waterfall under bearing’s inner race fault

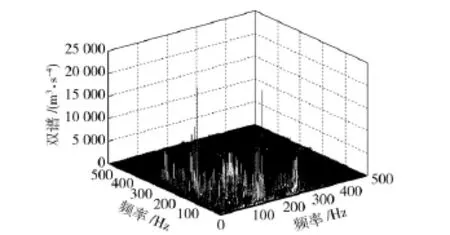
图5 轴承外圈故障双谱瀑布图Fig.5 Bispectrum waterfall under bearing’s outer race fault

2.2 双谱熵特征提取与分析

2.2.1 全频域的双谱熵特征

根据文中所建立的双谱熵模型，在0～500 Hz频带内计算测试信号的双谱熵，选取测点4、5 的计算结果作为故障模式识别的特征向量。3 种转速下各取5 个测试样本，4 种工况共取60 个样本进行分析计算，图6～图8为测点4、5 双谱熵分布散点图。从图中可以看出，正常工况下，信号不确定因素较少，复杂度小，信息熵数值较小，随着系统发生故障，振动信号的不确定性增大，复杂度提高，信息熵增大，信息熵的大小反映了各种故障引起齿轮箱振动特性变化的程度。测点4 的双谱熵基本能够识别上述4 种故障，测点5 离故障部位比测点4 近，其特征参量的离散度大，与测点4 相比分辨故障的能力较差，无法分辨两种轴承故障。但上述两测点均能判断出齿轮箱是否发生故障，从其他4 个测点的散点图中也可以得到相同的结论，分辨能力要比这两个测点差。

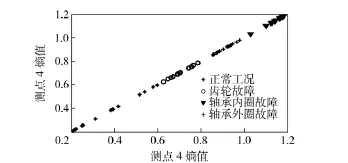
图6 测点4 双谱熵散点图Fig.6 Bispectrum entropy scatter gram for point No.4

图7 测点4、5 双谱熵散点图Fig.7 Bispectrum entropy scatter gram for point No.4 ＆ No.5

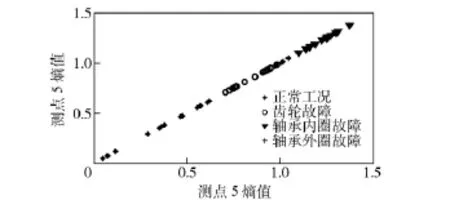
图8 测点5 双谱熵散点图Fig.8 Bispectrum entropy scatter gram for point No.5

2.2.2 频域分段双谱熵特征

在0～500 Hz 频带内，将信号双谱分为8 个频段，即(0～62.5 Hz，0～500 Hz)，(62.5～125 Hz，0～500 Hz)，…，(537.5～500 Hz，0～500 Hz)，计算各频段的双谱熵，作为故障模式识别的特征向量，仍以测点4 为例，4 种工况共60 个样本进行分析计算，图9～图12 为测点4 的8 个频段内的双谱熵分布图。从图中可以看出，各种工况下，后4 个频段的熵值位于不同的熵带，变化都很稳定，如正常工况0.3～0.55，齿轮故障0.7～0.9，轴承内圈故障0.85～1.05，轴承外圈故障0.45～0.95，轴承外圈故障工况下熵带的分散性最大。采用后4 个频段的双谱熵可识别是否存在故障。前4 个频段的双谱熵在其熵带范围内呈一定规律变化，不同工况的变化规律不同，可识别出故障的类型。

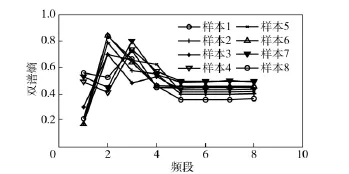
图9 正常工况测点4 双谱熵变化曲线Fig.9 Bispectrum entropy varying curve for point No.4 in normal state

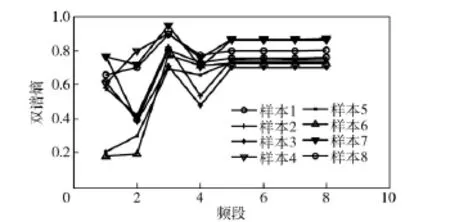
图10 齿轮故障工况测点4 双谱熵变化曲线Fig.10 Bispectrum entropy varying curve for point No.4 in gear’s fault

2.3 基于双谱熵特征和BP 网络故障模式识别

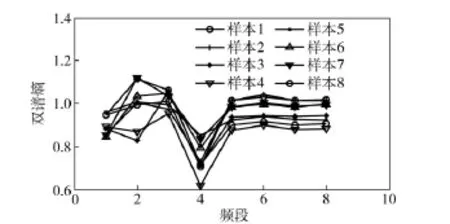
图11 轴承内圈故障工况测点4 双谱熵变化曲线Fig.11 Bispectrum entropy varying curve for point No.4 in bearing’s inner race fault

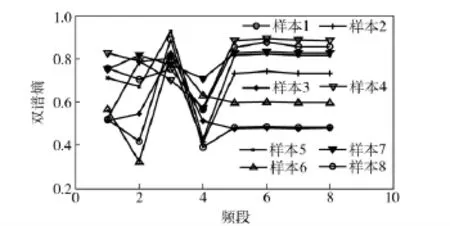
图12 轴承外圈故障工况测点4 双谱熵变化曲线Fig.12 Bispectrum entropy curve for point No.4 in bearing’s outer race fault

以测点4、5 的双谱熵特征参量为输入，建立2 ×5 ×4 的3 层BP 神经网络1;同时以测点4 的8 频段双谱熵特征参量为输入，建立8 ×5 ×4 的3 层BP 神经网络2，分别进行故障模式识别，训练样本为48 个，测试样本为12 个，两网络均以较快速度收敛到目标精度0.000 1，图13 为两网络的误差—迭代次数曲线。经测试样本进行测试，两网络均能正确识别本文中所列的4 种典型故障模式，表2为网络在各种工况下的理想输出，表3为网络1 的实际输出结果。从表2和表3中可以看出，网络的实际输出与理想输出存在误差，最大误差为0.012 126，均方误差为0.002 806，若将识别误差阈值设置为0.05，则上述网络的识别率为100%.以上诊断结果表明，利用双谱熵作为特征参量进行故障模式识别，特征向量个数少，网络简单，不管是单测点还是多测点，均能获得较高的诊断精度。

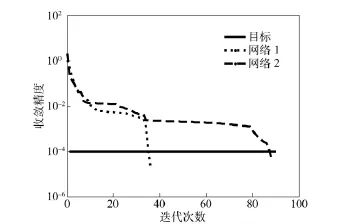
图13 网络1 和网络2 的收敛曲线Fig.13 Convergence curves of neural network 1 and 2

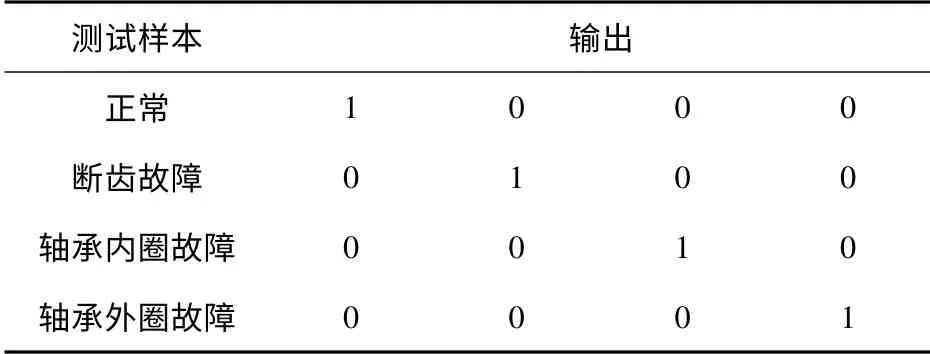
表2 测试样本的理想输出Tab.2 Desired output of test samples

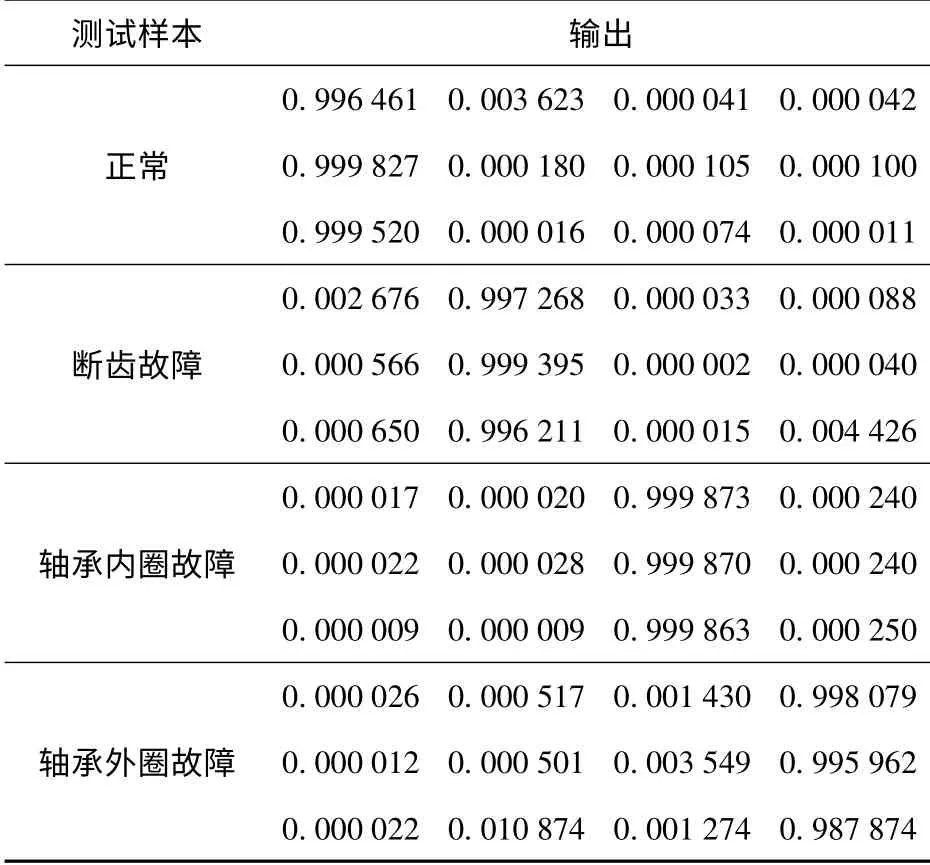
表3 测试样本的实际输出Tab.3 Output of test samples

4 结论

本文在双谱域内提取振动信号的故障特征参量，以解决齿轮箱振动信号复杂，敏感故障特征参量较难获得的问题。

根据振动信号的特点，在子空间分布概率下研究振动信号的信息熵，提出基于子空间分布概率的双谱熵模型和基于双谱熵特征参量的故障模式识别方法。经建立BP 神经网络识别验证，文中所提出的双谱熵特征参量对齿轮、轴承故障均比较敏感，用较少的测点可获得较高的诊断精度。

References)

［1］ 李杨寰，高峰，李腾，等.特征选择中信息熵的应用［J］.计算机工程与应用，2009，45(15):54－57.LI Yang－huan，GAO Feng，LI Teng，et al.Novel method for feature selection based on entropy［J］.Computer Engineering and Applications，2009，45(15):54－7.(in Chinese)

［2］ Bein B.Entropy［J］.Best Practice＆Research Clinical Anaesthesiology，2006，20(1):101－109.

［3］ Overbey L A，Todd M D.Effects of noise on transfer entropy estimation for damage detection［J］.Mechanical Systems and Signal Processing，2009，23:2178－2191.

［4］ Li Bing，Zhang Peilin，Liang Shubao，et al.Feature extraction and selection for fault diagnosis of gear using wavelet entropy and mutual information［C］∥Proceedings of 9th International Conference on Signal Processing.IEEE，2008:2846－2850.

［5］ 耿俊豹，黄树红，陈非，等.基于信息熵贴近度的旋转机械故障诊断［J］.华中科技大学学报:自然科学版，2006，34(11):93－95.GENG Jun－bao，HUANG Shu－hong，CHEN Fei，et al.Rotating machinery fault diagnosis based on close degree to information entropy［J］.Journal of Huazhong University of Science and Technology:Nature Science Edition，2006，34(11):93－95.(in Chinese)

［6］ Yu D J，Yang Y，Cheng J S.Application of time－frequency entropy method based on Hilbert－Huang transform to gear fault diagnosis［J］.Measurement，2007，40:823－830.

［7］ 于德介，张嵬，程军圣，等.基于EMD 的时频熵在齿轮故障诊断中的应用［J］.振动与冲击，2005，24(5):26－27.YU De－jie，ZHANG Wei，CHENG Jun－sheng，et al.Application of time－frequency entropy to gear fault diagnosis based on EMD［J］.Journal of Vibration and Shock，2005，24(5):26－27.(in Chinese)

［8］ Mammone N，Morabito F C.Enhanced automatic artifact detection based on independent component analysis and Renyi’s entropy［J］.Neural Networks，2008，21:1029－1040.

［9］ 陈进，姜鸣.高阶循环统计量理论在机械故障诊断中的应用［J］.振动工程学报，2001，14(2):126－134.CHEN Jin，JIANG Ming.The state－of－art of the application of the higher－order cyclostationary statistics in mechanical fault diagnosis［J］.Journal of Vibration Engineering，2001，14(2):126－134.(in Chinese)

［10］ 王华民，陈霞，安钢，等.基于高阶累积量的齿轮箱故障诊断研究［J］.机械强度，2004，(3):247－249.WANG Hua－min，CHEN Xia，AN Gang，et al.Fault diagnosis of gearbox based on higher order cumulants［J］.Journal of Mechanical Strength，2004，(3):247－249.(in Chinese)

［11］ Ai S F.Gear fault detection and diagnosis based on order bispectrum［C］∥Proceedings of 6th International Conference on Fuzzy Systems and Knowledge Discovery.United States:IEEE Computer Society，2009:463－467.

［12］ 谢平.故障诊断中信息熵特征提取及融合方法研究［D］.秦皇岛:燕山大学，2006.XIE Ping.Study on information entropy feature extraction and fusion methods in fault diagnosis［D］.Qinhuangdao:Yanshan University，2006.(in Chinese)