基于分数阶傅里叶变换的线性调频脉冲时延估计特性分析

邓兵，王旭，陶然，刘贤忠

(1.海军航空工程学院 电子信息工程系，山东 烟台264001;2.北京理工大学 电子工程系，北京100081)

时延估计是信号处理领域中参数估计的一项重要内容，时延估计的性能直接影响着定位系统的性能，因而成为雷达、声纳等的研究热点之一［1-2］。目前，关于时延估计的方法主要有:相关时延估计［3-4］、基于Hilbert 变换的时延估计［5-6］、子空间分解时延估计［8-9］、高阶统计量时延估计［9-11］等。随着分数阶傅里叶变换(FRFT)理论的不断发展，作为傅里叶变换的广义形式，FRFT 以其独具的优势而得到了越来越多的应用［12］。2009年，Tao 等［13］提出了一种基于FRFT 的线性调频(LFM)脉冲时延估计方法，并从输出噪声和估计有效性两个方面进行了分析。众所周知，针对宽带LFM 脉冲的时延估计问题最为经典的方法就是脉冲压缩(也就是匹配滤波时延估计或相关时延估计)，并被广泛应用于高分辨力雷达的数据处理中。相比于脉冲压缩，文献［14］的方法运算复杂度更低(约减少1/2)，且更便于与时频滤波、波束形成［15］等FRFT 的其他应用相组合，因此，也就具有更大的应用前景，如阵列合成孔径雷达［16］。不同的是，脉冲压缩特性体现在时域，而基于FRFT 的LFM 脉冲时延估计［13］的特性是表现在分数阶傅里叶域。考虑到时域和频域都是分数阶傅里叶域的特例，因此，本文以脉冲压缩的时域特性为参照，来分析基于FRFT 的LFM 脉冲时延估计的分数阶傅里叶域特性，并具体对比两者在数字信号处理上的差异，为该方法的进一步应用奠定基础。

1 预备知识

时延估计基本问题就是根据接收信号来快速准确地估计出其相对于发射信号的时间延迟，从而来得出目标距离。脉冲压缩技术则是为了解决简单脉冲信号的距离分辨力和作用距离相互矛盾的问题而提出的，其通过对大时宽带宽积信号进行脉压来同时获得长脉冲的大能量和短脉冲的高分辨。常用的大时宽带宽积信号有LFM 信号、二相编码信号等。其中，针对LFM 信号的脉冲压缩不仅应用于常规脉冲压缩雷达，也应用在合成孔径雷达。LFM 脉冲压缩的有关特性如下［1］:1)最大输出信噪比:2E/N0;2)脉宽压缩比:时宽带宽积D;3)压缩前后脉冲振幅比:D1/2.其中:E 为脉冲信号能量;N0为白噪声单边功率谱密度;D =TB 为脉冲信号的时宽带宽乘积，T 为脉冲持续时间，B 为脉冲信号带宽。

FRFT 是傅里叶变换的广义形式，它在统一的时频域上进行信号处理，作为一种线性变换，不受交叉项困扰，且具有与FFT 相当的快速算法。近年来出现了许多基于FRFT 的信号处理方法，并已在信号分析与重构、信号检测与参数估计、变换域滤波、语音分析、图像处理、神经网络、模式识别、阵列信号处理和雷达、通信、声纳中得到了广泛的应用。FRFT 定义式如下:

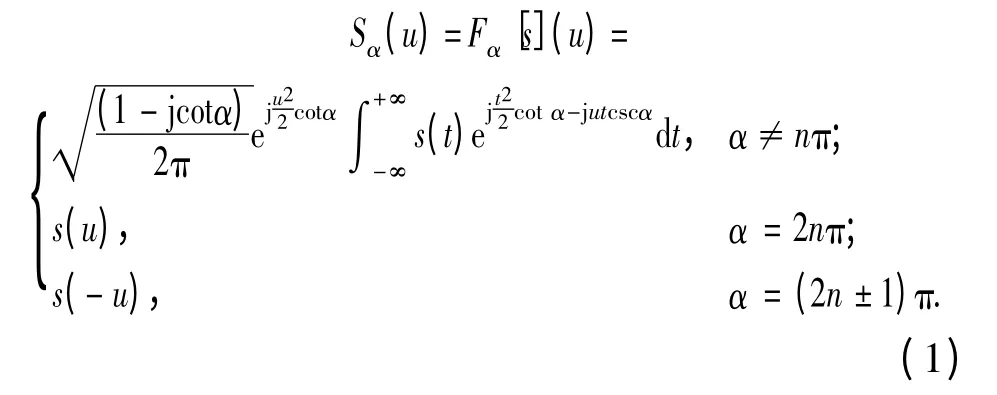
式中:α 为FRFT 阶数;Fα为FRFT 算子。

设接收信号为~s(t)=s(t-τ)，则有

因此，可以依据接收信号~s(t)的FRFT 谱峰值位置相对于参考信号s(t)的FRFT 谱峰值位置的位移情况来计算时延τ.相应的时延估计子为

2 分数阶傅里叶域特性分析

既然FRFT 以2π 为周期，不妨将α 取值区间设为［-π，π］.根据FRFT 相关理论［12］可知实现LFM信号能量聚集的最优FRFT 阶次为cot αm= -2πμ，那么可进一步限定αm∈(-π/2，π/2).因此有:

2.1 峰值输出信噪比

既然α 阶FRFT 等效为角度α 的时频面旋转，因此，白噪声在任意阶次的分数阶傅里叶域内能量分布仍然是均匀的。设白噪声的α 阶分数阶傅里叶功率谱密度为Nα，则有白噪声能量为:NαUαT，其中Uα为白噪声的α 阶分数阶傅里叶功率谱宽。根据帕赛瓦尔准则，显然有:

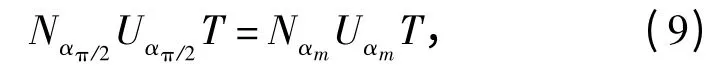
式中:Nαπ/2为白噪声的频域单边功率谱密度N0，这是因为当α=π/2 时FRFT 就等效为传统傅里叶变换。既然Uαπ/2|sin αm| =Uαm［17］，代入(9)式得到:

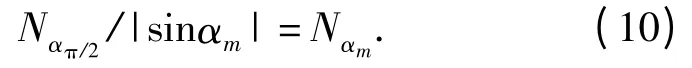
根据帕塞瓦尔准则可以知道FRFT 结果的模平方给出的是能量谱，也就是说，基于FRFT 的时延估计峰值表征的是LFM 脉冲在αm阶分数阶傅里叶域的能量聚集程度。因此，等效的αm阶分数阶傅里叶域峰值输出信噪比为

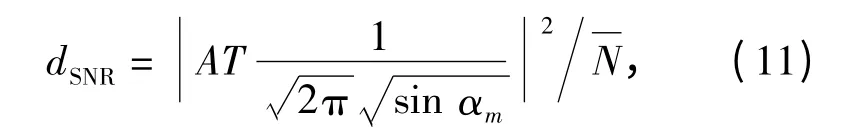
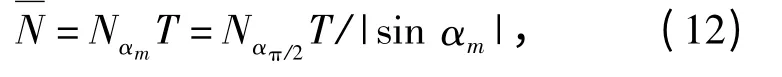
代入(11)式，得到:

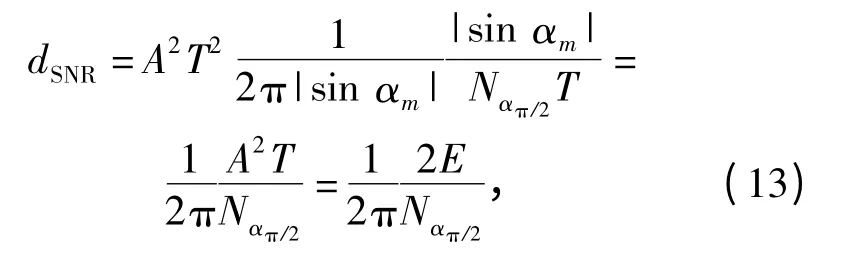
式中:E 为LFM 脉冲的能量。对比LFM 脉冲压缩的最大瞬时输出信噪比，两者相差常数1/2π，这是因为本文推导所用的FRFT 定义式采用的是角频率的原因。

2.2 脉宽压缩比

根据(2)式、(8)式，可知αm阶分数阶傅里叶域压缩后脉宽就是|Sαm(u)|的LFM 脉冲主瓣宽度。从(7)式可得

那么根据(8)式所示的时延估计子换算成多目标时延分辨力为

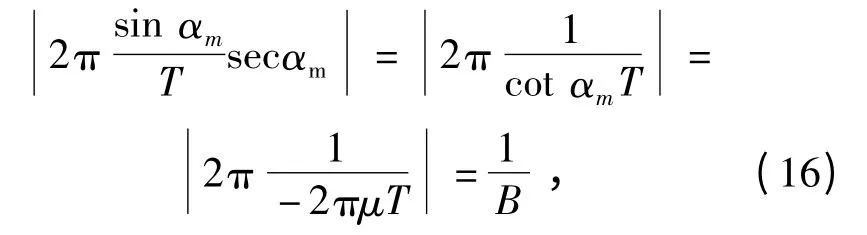
式中:B = |μT|为脉冲调频带宽。可以发现这与LFM 脉冲压缩的时延分辨力一致，因此，两者的脉宽压缩比均为T/B-1=D，即，时宽带宽积。

2.3 峰值振幅比

根据(14)式，可以得到压缩前后脉冲峰值振幅比为

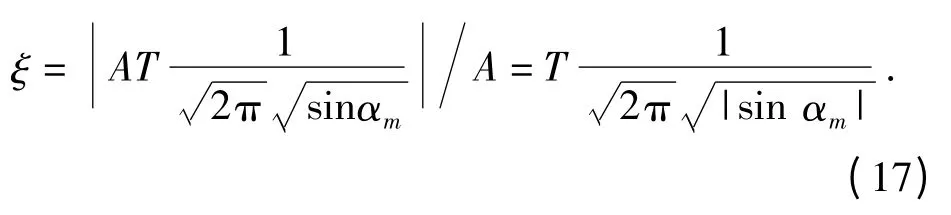
当αm→0 时，有|sin αm|→0，且有sin αm≈αm，cos αm≈1.既然cot αm= -2πμ，因此，从(17)式可知压缩前后脉冲峰值振幅比与脉冲宽度T 和调频率绝对值|μ|成正比。

当|μ|足够大时，有

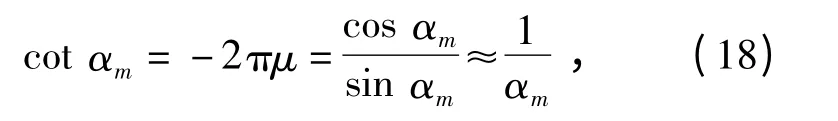
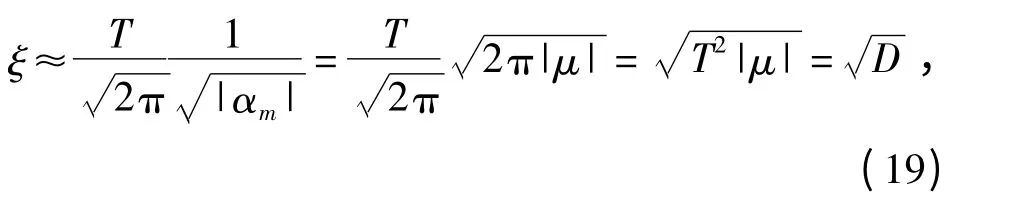
从(19)式可见:当|μ|足够大时，峰值振幅比约等于D1/2.

3 数字信号处理的性能比较

从前面的分析可以知道:基于FRFT 的LFM 脉冲时延估计与LFM 脉冲压缩的理论特性一致。不过，两者都可以采用数字信号处理的方式实现，那么在数字实现上两者是否存在性能差异呢?

设采样频率为fs，根据奈奎斯特采样定理有fs≥2B(不妨设fs=ηB，η≥2)，则采样周期LFM 脉冲压缩是在时域完成，则其数字实现的时延估计是以ts为步长来确定的。即，时延估计值来自于离散数值集{ts，2ts，…，Nts}，其中N =R/ts，R 为脉冲重复周期(一般情况下总可以选择R 为ts的整数倍)。这也就意味着无噪条件下LFM脉冲数字压缩的时延估计精度不会低于既然LFM 脉冲压缩后的脉宽为那么在满足奈奎斯特采样定理前提下LFM 脉冲压缩的数字实现方式对目标检测和时延估计影响可忽略。

基于FRFT 的LFM 脉冲时延估计是在分数阶傅里叶域内完成，那么根据(8)式所示的时延估计子可以知道时延估计值来自于离散数值集{us，2us，…，Nus}secαm，其中us为αm阶分数阶傅里叶域离散步长。由分数阶傅里叶域采样理论［17］可知:

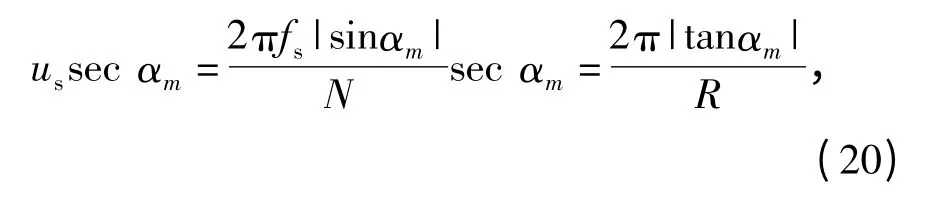
将cot αm= -2πμ 代入(20)式，可得:

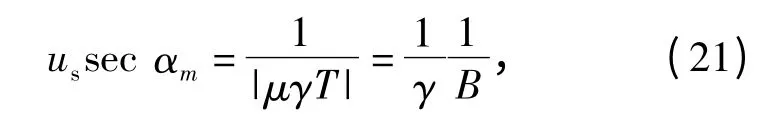
式中γ=R/T ＞1.显然，有

也就意味着，数字实现方式同样对基于FRFT 的LFM 脉冲时延估计没有影响。(注:上述推导是对整个脉冲重复周期的N 点数据作一次FRFT 的结果，如果采用的是分为H 段流水处理的方式，那么理论上只需要保证γ/H ＞1 即可，实际上为了保证足够的精度，最好保证γ/H≥5).

实际应用中一般有γ ＞η，也就是说，同样的数据率采用基于FRFT 的LFM 脉冲时延估计精度会优于LFM 脉冲压缩。而且，从上述分析也可以发现:在数字实现上，LFM 脉冲压缩通过提升采样频率来减小时延估计的离散步长ts，而基于FRFT 的LFM 脉冲时延估计是通过延长脉冲重复周期(或分段时长)来减小时延估计的离散步长ussecαm.

4 仿真

仿真所用数据如下:脉宽T =10 μs，调频带宽B=10 MHz，那么时延分辨力为1/B=0.1 μs，即距离分辨力约为15 m.观测距离区间取为［10 km，15 km］，设置有6 个目标，假定各目标强度相同，位置分别为10 500、11 000、12 000、12 010、13 000、13 020 m.仿真结果如图1和图2所示，可以看出:目标3 与目标4 的间距小于分辨力而不能区分，目标5 与目标6的间距大于分辨力而能够区分。

5 结论

本文以LFM 脉冲压缩的时域特性为参照，对比分析了基于FRFT 的LFM 脉冲时延估计特性，得到如下结论:

1)基于FRFT 的LFM 脉冲时延估计的峰值输出信噪比为与脉冲压缩最大输出信噪比相差系数1/2π.

2)αm阶分数阶傅里叶域压缩后脉宽是相应的多目标时延分辨力为1/B，脉宽压缩比同样为时宽带宽积。

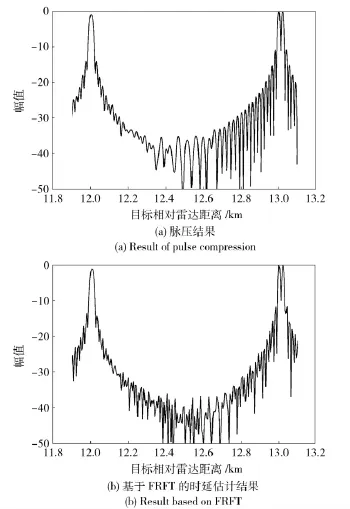
图2 局部放大对比图Fig.2 Zoom of Fig.1

4)如果采用数字信号处理来实现，两者的时延估计离散步长不一样。LFM 脉冲压缩依据采样频率的提升来减小离散步长，而基于FRFT 的LFM 脉冲时延估计则通过延长脉冲重复周期(或分段时长)来减小离散步长，因此，后者的精度往往更高，所需数据率可以更低。

References)

［1］ 丁鹭飞，耿富录，陈建春，等.雷达原理［M］.第4 版.北京:电子工业出版社，2009.DING Lu-fei，GENG Fu-lu，CHEN Jian-chun，et al.Radar theory［M］.4th ed.Beijing:Publishing House of Electronics Industry，2009.(in Chinese)

［2］ 向敬成.信号检测与估计［M］.北京:电子工业出版社，1994.XIANG Jing-cheng.Signal detection and estimation［M］.Beijing:Publishing House of Electronics Industry，1994.(in Chinese)

［3］ Quazi A H.An overview on the time delay estimate in active and passive systems for target localization［J］.IEEE Trans Acoustics，Speech and Signal Processing，1981，29(3):527 -533.

［4］ Knapp C，Carter G.The generalized correlation method for estimation of time delay［J］.IEEE Trans Acoustics，Speech and Signal Processing，1976，24(4):320 -327.

［5］ Cabot R C.A note on the application of the Hilbert transform to time delay estimation［J］.IEEE Trans Acoustics，Speech and Signal Processing，1981，29(3):607 -609.

［6］ Hussain Z M，Boashash B.Hilbert transformer and time delay:Statistical comparison in the presence of Gaussian noise［J］.IEEE Trans Signal Processing，2002，50(3):501 -508.

［7］ Cedric L B，Vincent B，Wang Y D.Modified ESPRIT(M-ESPRIT)algorithm for time delay estimation in both any noise and any radar pulse context by a GPR radar［J］.Signal Processing，2009，90(1):173 -179.

［8］ Ge F X，Shen D X，Peng Y N，et al.Super-resolution time delay estimation in multipath environments［J］.IEEE Trans Circuits and Systems-I，2007，54(9):1977 -1986.

［9］ Govindan R B，Raethjen J，Kopper F，et al.Estimation of time delay by coherence analysis［J］.Physica A:Statistical Mechanics and its Applications，2005，350(2 -4):277 -295.

［10］ Liang Y C，Leyman A R.Time delay estimation using higher order statistics［J］.Electronics Letters，1997，33(9):751 -753.

［11］ Wu Y.Time delay estimation of non-Gaussian signal in unknown Gaussian noises using third-order cumulants ［J］.Electronics Letters，2002，38(16):930 -931.

［12］ 陶然，邓兵，王越.分数阶傅里叶变换理论及应用［M］.北京:清华大学出版社，2009.TAO Ran，DENG Bing，WANG Yue.Fractional Fourier transform and its applications［M］.Beijing:Tsinghua University Press，2009.(in Chinese)

［13］ Tao Ran，Li Xue-Mei，Li Yan-Lei，et al.Time delay estimation of chirp signals in the fractional Fourier domain［J］.IEEE Trans Signal Processing，2009，57(7):2852 -2855.

［14］ 邓兵，陶然，齐林，等.分数阶Fourier 变换与时频滤波［J］.系统工程与电子技术，2004，26(10):1357 -1359.DENG Bing，TAO Ran，QI Lin，et al.Fractional Fourier transform and time-frequency filtering［J］.Systems Engineering and Electronics，2004，26(10):1357 -1359.(in Chinese)

［15］ Yetik I S.Beamforming using fractional Fourier transform［J］.IEEE Trans Signal Processing，2003，51(6):1663 -1668.

［16］ 吴曼青，葛家龙.数字阵列合成孔径雷达［J］.雷达科学与技术，2009，7(1):1 -9.WU Man-qing，GE Jia-long.Digital array synthetic aperture radar［J］.Radar Science and Technology，2009，7(1):1 -9.(in Chinese)

［17］ Tao Ran，Deng Bing，Zhang Wei-qiang，et al.Sampling and sampling rate conversion of band limited signals in the fractional Fourier transform domain［J］.IEEE Trans Signal Processing，2008，56(1):158 -171.