防空火箭炮递阶控制策略设计

杨帆，马大为，乐贵高，姚佳

(1.南京理工大学 机械工程学院，江苏 南京210094;2.东南大学 电气工程学院，江苏 南京210096)

由于战略的需要，火箭炮逐渐由压制型武器向精确打击型防空武器转变。防空火箭炮运行过程中，由于存在弹炮质量比大而造成的转动惯量变化大、强大的燃气流力矩的干扰和大范围的参数摄动等因素［1］，传统火炮控制理论已无法满足系统指标要求，而新兴的控制理论，如神经网络、模糊控制、内模控制等逐渐得到重视［2］。

滑模控制是近年研究的热点，由于其具有完全的鲁棒性，控制器结构简单、易于实现［3］等特点，在导弹自动驾驶仪设计［4］、飞行器姿态控制［5］等军工领域得到广泛应用。但由于滑模控制本质上的开关特性会引起控制信号的抖振，从而影响控制精度，甚至损害系统的机械结构，故需考虑抑制控制信号的抖振。文献［1－3］均未提出抑制抖振的方法;文献［4－5］分别使用动态滑模与自适应滑模，削弱了控制信号的抖振，但控制器结构较复杂，工程上不易实施;文献［6］通过渐进状态观测器为控制量中的高频成分提供高频旁路，消除了由未建模动态引起的输出位移的抖振，但其控制输入量的平滑度仍有待提高。

针对上述问题，笔者结合由Saridis 提出的递阶理论，针对防空火箭炮运行时的特点，设计了改进型递阶控制策略。其中决策级算法用于实时修改控制器参数;实时控制级采用新型二阶滑模算法，消除了输入至控制器的信号的畸变，同时所选切换函数能使其所确定的滑动模态渐近稳定且具有良好的动态性能，保证防空火箭炮在满足指标的条件下平稳地运行。

1 防空火箭炮数学模型

防空火箭炮由方位子系统与俯仰子系统构成，其数学模型一致。

1.1 基于电流解耦的永磁同步电机线性化模型

假设:1)忽略电机铁心的饱和;2)不计电机的涡流和磁滞损耗;3)转子没有阻尼绕组;4)励磁电流无动态响应;5)电动机气隙磁场均匀分布，感应反电动势呈正弦波状［7］;6)采用转子磁极位置定向矢量控制时定子电流励磁分量id=0.

由上述，可得dq 坐标轴下，解耦后的永磁同步电机线性化数学模型［1］:

式中:ud与uq分别为dq 坐标系上的电枢电压分量;iq与L 为dq 坐标系上的电枢电流分量和等效电枢电感;R 与ωr(=pnωm)分别为电枢绕组电阻和dq坐标系的电角速度;ψf与pn为永久磁铁对应的转子磁链和电机极对数;Tem与TL分别为电磁转矩和负载力矩;B 与J 分别为阻尼系数和转动惯量;Kt为电磁转矩系数。

1.2 被控对象数学模型

系统电流环采用滞环比例控制，Kcp为电流环控制参数;速度环采用比例控制，Kvp为控制参数，Kv为速度反馈系数，iq为控制电流，ωm为电机轴输出角速度，ωd为输入角速度即控制量u，系统结构如图1所示。

速度环输出ωm经减速器到达位置输出θm，该环节传递函数为

式中Kj为减速比系数。

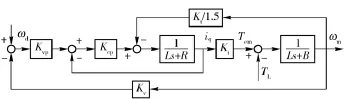
图1 系统速度环结构框图Fig.1 Block diagram of system with velocity loop

令x1=θm，x=［x1x2x3］T，可得防空火箭炮系统的状态方程:

2 控制算法设计

2.1 控制策略描述

经典的递阶控制由3 个基本控制级构成，分别为组织级、协调级和执行级［8］。防空火箭炮接收炮位计算机的位置指令，属于随动设备，故取消传统递阶控制中的组织级，设计包括决策级与实时控制级在内的两层递阶控制结构。

2.2 决策级算法

决策级算法负责计算实时转动惯量J.

某型号防空火箭炮样机由转塔与发射箱两部分构成。火箭炮发射箱通过耳轴连接至转塔，发射箱单边4 ×4 管，空载时质量为m1;左右发射箱共计32管。将发射管编号为Gij，其中i =1，2，3，4，j =1，2，3，4，5，6，7，8，载弹时Gij=1，无弹时Gij=0，该状态由载弹传感器得知。

转塔由俯仰系统与方位系统构成，方位转角范围为0°～360°，俯仰转角范围为0°～70°.

俯仰轴系转动惯量计算如下:假设:1)空载时，发射箱对俯仰轴的转动惯量为J1e;2)第ij 管中装入12 kg 火箭弹，对俯仰轴增加的转动惯量为J1ij，实际设计中很难保证发射箱质心与转动轴重合，设质心与俯仰轴心距离为L1，则俯仰轴系的转动惯量J1可表示为:

方位轴系转动惯量计算如下:假设:1)转塔对方位轴的转动惯量为J2e;2)俯仰角0°且空载时，发射箱对方位轴的转动惯量为J*1;3)俯仰角0°时，第ij 管中装入12 kg 火箭弹，对方位轴增加的转动惯量为J2ij，单边发射箱质心距回转轴L2，θ 为俯仰角，则俯仰轴系转动惯量J2可近似表示为

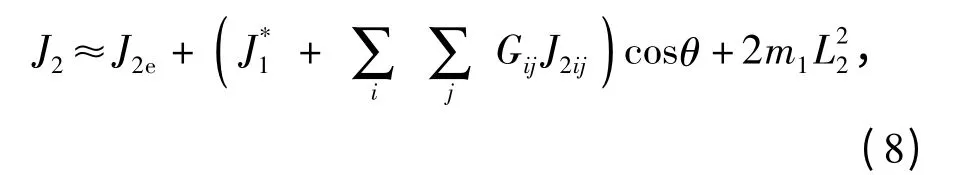
式中:L1，L2，J*1，J1e，J2e，m1是已知量，J1ij和J2ij根据发射管位置的不同，可计算得出。

2.3 实时控制级算法

实时控制级采用二阶滑模控制策略，控制结构如图2所示。

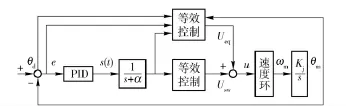
图2 滑模位置控制器结构图Fig.2 Block diagram of sliding－mode position controller

由(6)式，可将本系统描述为

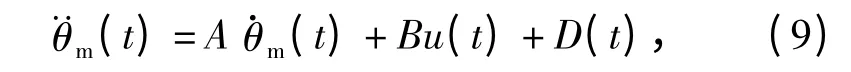
式中:A=－a2/a1，B=b/a1，D(t)=－ θ···m/a1－d(t)，将D(t)视为扰动量，Dmax为D(t)的最大值，即

输入控制量u 可表示为

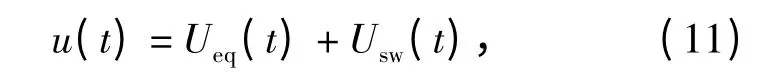
式中:Ueq(t)为等效控制律;Usw(t)为切换控制律。

设θd是来自炮位计算机的未来点位置信息，θm是系统的位置反馈信息，则跟踪误差e 定义为

由(9)式和(12)式得到

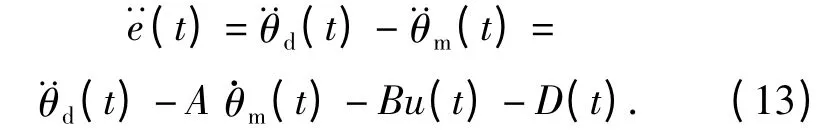
本文对PID 切换函数［9］进行优化如下

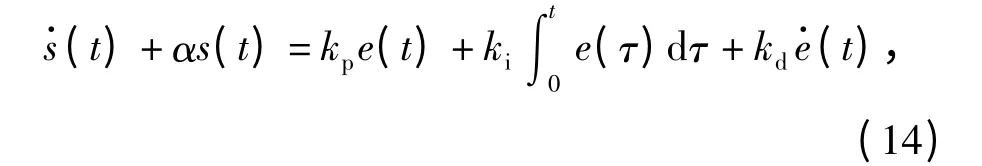
式中:kp，ki，kd分别为比例、积分、微分增益;α 为低通滤波器常数。

滑模面的二阶导数可表示为

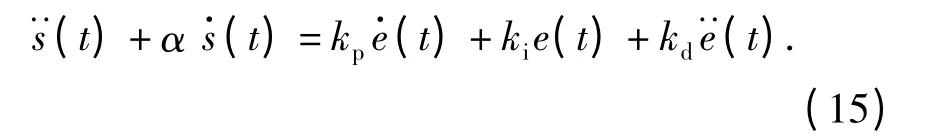
将(13)式代入(15)式有

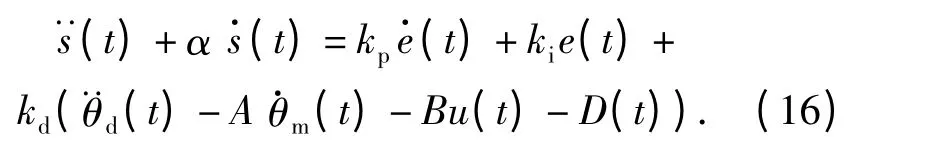
按照指数趋近律设计切换控制律为

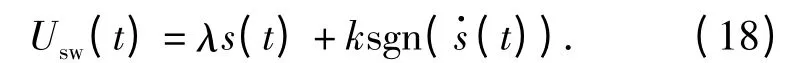
考虑控制律满足滑模控制达到条件，系统稳定，此时要求λ ＞1/(Bkd)且k ＞Dmax/B.

2.4 参数选择与控制律优化

切换控制律Usw为弥补扰动D(t)带来的影响。(19)式要求k ＞Dmax/B，若k 值选取过小，会降低控制器的鲁棒性甚至影响到系统的稳定性;反之，则造成多余的控制输入从而产生抖振。在防空火箭炮运行过程中，主要承受静阻力矩和动态力矩［10］，其值是可估计的，可在此基础上合理设定k值。

另外，由于(18)式中存在开关函数，其不连续的特性也会引发抖振，故使用Sigmoid 形函数tanh(·)代替sign(·)，将(18)式改写为

2.5 微分估计器

本文设计的控制策略需使用相关数据的一阶或高阶微分项，这些信息无法直接测量获得。为避免差分法中存在的信号畸变与噪声敏感等问题，微分估计器被广泛使用。本文直接使用文献［11］的成果。

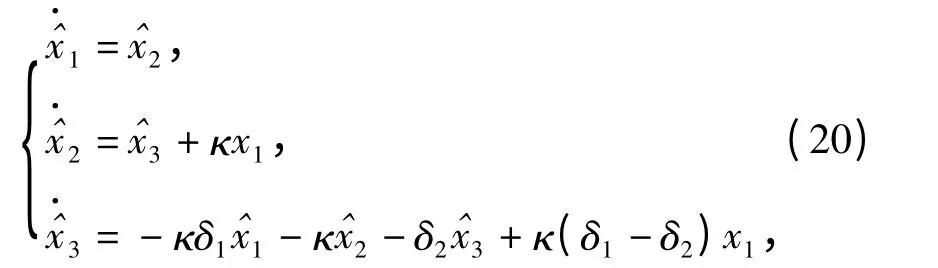
式中:δ1=8，δ2=9δ1，κ =27δ21为设计参数，x1是输入值，由获得x1的一阶微分估计值，由+κx1获得x1的二阶微分估计值。

3 仿真与分析

仿真对象为防空火箭炮俯仰子系统，设计指标为:最大跟踪角速度50°/s，最大跟踪角加速度55°/s2，定位误差小于1 mil，跟踪误差小于4 mil.

将表1参数代入(6)式得:A=－0.345 5/J，B=2.184 8/J，其中J 由(2)式获得。控制器参数:kp=22，ki=0.1，kd=0.51，λ =12，φ =1.1，α =160，k =2.5，kcp=10，kvp=10.PID 控制器位置环参数:kp=20，ki=0，kd=0.24.算法选择ODE45，仿真步长为0.001 s.

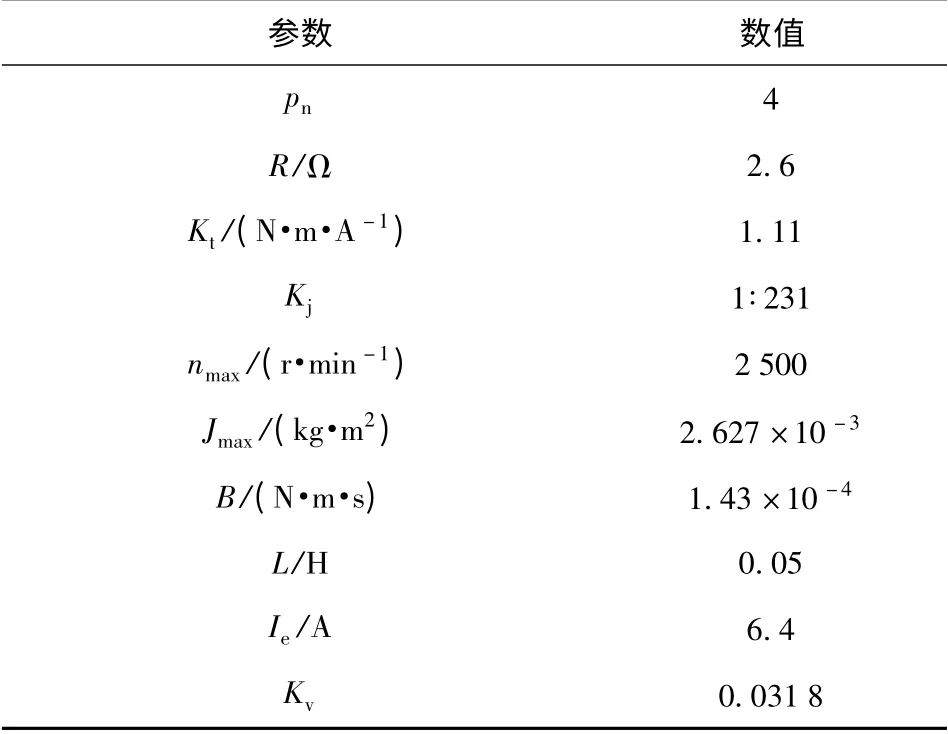
表1 俯仰子系统参数Tab.1 Parameters of elevation system

控制输入量u∈［－10 V，10 V］，以电压形式输入到驱动器中，对应电机转速－2 200～2 200 r/min.

图3和图5中，PID 表示使用PID 加二阶前馈控制响应曲线，2－SMC 表示采用基于二阶滑模控制的递阶控制策略的响应曲线。

1)给定正弦信号θd=30sin(πt/2)，假定火箭炮俯仰子系统在30°～60°角之间做正弦运动，电机轴上加载干扰TL=15sin(20πt).采用PID 控制与二阶滑模控制的跟踪误差曲线如图3所示。

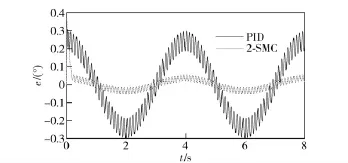
图3 跟踪误差曲线Fig.3 Tracking error

无负载扰动时的二阶滑模控制输入曲线如图4(a)所示，输出扭矩如图4(b)所示，可看出，在无扰动情况下，控制输入平滑;带负载扰动时的二阶滑模控制输入曲线如图4(c)所示，输出扭矩如图4(d)所示，表示输出转矩有效抵消了干扰力矩TL.

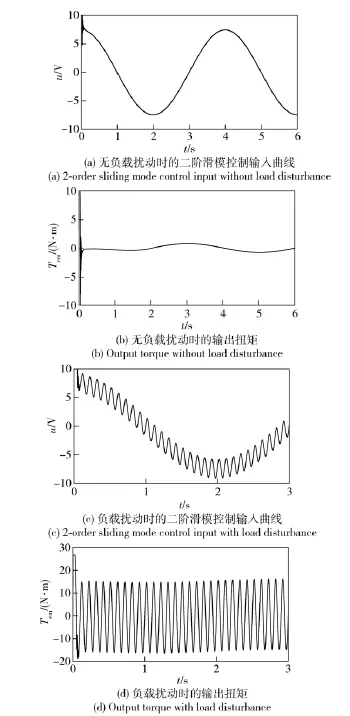
图4 二阶滑模控制输入及输出转矩Fig.4 2－order sliding mode control input and output torque

2)给定阶跃信号t=0 s 时θd=15°，1 s 后在电机轴间隔0.2 s 加载幅值为15 N·m，持续时间为0.01 s 的脉冲力矩来模拟火箭炮发射时的冲击载荷。阶跃信号的响应曲线如图5(a)所示;图5(b)为响应曲线局部放大图;该条件下控制输入如图5(c)所示，可看出控制输入相对平滑，在遇到扰动时有相应的切换控制输入保证火箭炮位置环的稳定。

4 实验验证

在某交流伺服实验台上进行实验验证，系统的控制周期为10 ms.图6和图7中，PID 表示使用PID 加二阶前馈控制响应曲线，2－SMC 表示采用基于二阶滑模控制的递阶控制策略的响应曲线，伺服系统与控制器参数如第3 节所述。

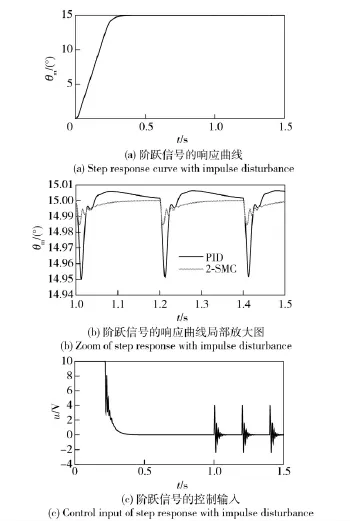
图5 阶跃响应与控制输入曲线Fig.5 Step response and control input

1)系统满惯量负载，给定曲线50°sin(0.3πt)，采用不同控制方法的误差曲线对比如图6所示。

该条件下跟踪误差最大值不超过0.18°，均方差为0.048 7°(＜4 mil)，满足指标要求。

2)控制器参数不变，系统惯量减小至原惯量的2/5，模拟空载后的情况。给定曲线50°sin(0.3πt)，跟踪误差曲线如图7所示，表明采用的控制策略跟踪精度较高，且对转动惯量变化不敏感。

该条件下跟踪误差最大值不超过0.15°，均方差为0.042 4°(＜4 mil)，满足指标要求。

3)控制器参数不变，满惯量负载，0 s 时刻，给定阶跃信号θd=50°，响应曲线如图8所示。

该条件下系统最大超调量为0.459 4°，调节时间小于1 s，此时稳态误差仅为0.014 6°(≤1 mil)，系统恢复稳定，响应时间满足指标要求。

5 结论

本文提出一种改进型递阶控制策略。

图6 满惯量负载跟踪误差曲线Fig.6 Tracking error with full－load inertia

图7 2/5 惯量负载跟踪误差曲线Fig.7 Tracking error with 2/5－load inertia

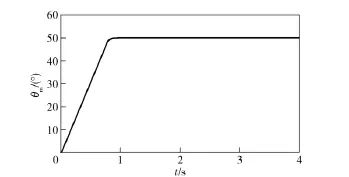
图8 满惯量阶跃响应曲线Fig.8 Step response with full－load inertia

1)将递阶控制思想应用防空火箭炮的控制中，控制律中显含J，使控制输入弥补了由惯量变化造成的参数摄动。

2)设计新型切换函数，将误差进行滤波及PID变换处理，消除了信号的畸变，通过分析扰动的方法合理设定滑模增益k，有效抑制了控制输入量的抖振。

3)加入微分估计器，能较准确地获得相关信息的微分估计值。

结果表明，该控制策略可以有效抑制防空火箭炮系统的参数摄动与外部扰动造成的影响，输入控制曲线相对平滑，控制器的可行性、实时性和控制精度皆能满足指标的要求，与传统的控制策略相比，有一定的优势与应用价值。

References)

［1］ 朱玉川，马大为，李志刚，等.带积分项的火箭炮优化滑模伺服控制［J］.兵工学报，2007，28(10):1272－ 1275.ZHU Yu－chuan，MA Da－wei，LI Zhi－gang，et al.Optimal sliding mode servo control with integral term for rocket launcher［J］.Acta Armamentarii，2007，28(10):1272－1275.(in Chinese)

［2］ 柴华伟.某集束防空火箭炮位置伺服系统的鲁棒控制与应用研究［D］.南京:南京理工大学，2008.CHAI Hua－wei.Robust control and application research on position servo system of cluster antiaircraft rocket launcher［D］.Nanjing:Nanjing University of Science and Technology，2008.(in Chinese)

［3］ 孙常胜，陈杰，窦丽华.基于最优化的坦克稳定器滑动模态变结构控制［J］.兵工学报，2001，22(1):15－18.SUN Chang－sheng，CHEN Jie，DOU Li－hua.Variable structure control for sliding mode of tank stabilizator based on optimization［J］.Acta Armamentarii，2001，22(1):15－18.(in Chinese)

［4］ 尚安利，于德海，顾文锦.基于动态二阶滑模控制算法的导弹自动驾驶仪设计［J］.兵工学报，2006，27(1):50－53.SHANG An－li，YU De－hai，GU Wen－jin.Missile autopilot design based on dynamic second order sliding mode control［J］.Acta Armamentarii，2006，27(1):50－53.(in Chinese)

［5］ 段洪君，史小平.基于滑模自适应的飞行器鲁棒姿态控制［J］.兵工学报，2009，30(7):1004－1008.DUAN Hong－jun，SHI Xiao－ping.Robust attitude control for micro air vehicle based on sliding adaptive algorithml［J］.Acta Armamentarii，2009，30(7):1004－1008.(in Chinese)

［6］ SUN Chang－sheng，TIAN Jie，CHEN Jie，et al.Optimal sliding mode variable structure control of servo regulators with asymptotic observers［C］∥Proceedings of the 3th World Congress on Intelligent Control and Automation.IEEE，2000，4:3021－3025.

［7］ GUO Ya－jun，MA Da－wie，LE Gui－gao.Backstepping and sliding mode cascaded compound control for AC position servo system［C］∥Asia Pacific Conference on Postgraduate Research in Microelectronics ＆ Electronics.IEEE，2009:145－148.

［8］ Valavanis K P，Saridis G N.Probabilistic modeling of intelligent robotic systems［J］.IEEE Transaction on Robotic and Automation，1991，7(1):164－ 171.

［10］ 朱玉川.某箱式多管火箭炮快速装填与高精度自动操瞄系统研究［D］.南京:南京理工大学，2006.ZHU Yu－chuan.Research on rapid loading and high precision automatic operating ＆ aiming system of a certain canister multiple rocket launcher［D］.Nanjing:PhD Dissertation，Nanjing University of Science and Technology，2006.(in Chinese)

［11］ 齐国元.非线性系统新型估计器及其在控制中的应用［D］.天津:南开大学，2004.QI Guo－yuan.New style estimators for nonlinear systems and applications in control［D］.Tianjin:Nankai University，2004.(in Chinese)