考虑参数随机性的供输弹系统动力学及动作可靠性仿真研究

李伟，马吉胜，狄长春，吴大林

(1.海军航空兵学院 教研部，辽宁 葫芦岛125001;2.军械工程学院 火炮工程系，河北 石家庄050003)

供输弹系统是大口径自行火炮实现爆发射速和持续射速的关键辅助系统，其性能好坏、可靠性高低直接关系到在严酷的战争环境下自行火炮能否有效发扬火力。供输弹系统是集机电液一体化的复杂系统，其动力学涉及机、电、液等领域的耦合。在建立其动力学模型时必须充分考虑机电液系统之间的耦合效应，建立完整的包括机、电、液在内的闭环模型，从而提高求解精度，真正满足实时动态仿真的需求。

供输弹系统工作过程受多种随机参数的影响，其动力学响应是一个随机过程。基于确定参数的动力学分析得到的计算结果仅仅是随机响应中的一个元素，难以全面描述供输弹系统的动力学特性。并且由参数随机性引起的机构动作可靠性问题也无法得到阐释。从调研结果来看，供输弹系统的故障多数并不是由零部件的失效引起的，往往是由于供输弹系统的输出指标达不到规定要求而导致的系统工作循环终止，属于机构动作可靠性的范畴。因而，研究考虑参数随机性的供输弹系统动力学不仅是全面掌握其动力学特性的有效途径而且对研究系统动作可靠性具有很重要的现实意义。

1 供输弹系统机电液耦合动力学模型

1.1 供输弹系统工作过程

供输弹系统可以完成0°～65°任意角装填，输弹过程为2 级输弹。1 级输弹时，双联泵大泵单独供油，马达经齿轮传动带动链轮驱动链条推送弹丸，并通过挂钩带动推壳小车一起运动;当推壳小车运动到限位槽后与链条脱钩完成排壳;当链条伸出一定长度后，电磁阀控制双泵供油，开始2 级输弹;输弹到位后，电磁阀控制马达反转将链条收回;当链条快回收到位时，小泵单泵供油完成收链。

1.2 机电液耦合动力学模型的建立

利用MSC.Adams 和Easy5 仿真平台构建供输弹系统机电液耦合动力学模型，其联合仿真结构如图1所示。图中x、分别为链条位移和速度，用于在MSC.Easy5 中建立控制方程;MAdams为链轮驱动力矩，通过函数Varval(MEasy5)将液压系统中马达输出力矩MEasy5赋予MAdams;为链轮转速，用于在MSC.Easy5 中建立压力和流量方程;pin、Qin和pout、Qout分别为液压马达进出口压力和流量。

供输弹系统的拓扑结构［1］如图2所示。H1为固定铰，H3为齿轮箱输出轴与链轮间也联轴器连接，简化为固定铰，H2、H7、H1c、H5c、H6c为旋转铰，H4、H5、H6、H8、H9、H10、H11、H2c、H4c为非完整约束。

模型中通过定义碰撞铰进行非完整约束的定义，H3c为平移铰。对往复推送式输弹链条B4进行了详细的建模，其共有链节45 个，滚子45 个，1 个链头。链节间采用旋转铰，链节滚子与链轮及链条箱隔板间通过碰撞铰实现力的传递和自由度的约束。

图1 供输弹系统联合仿真结构Fig.1 Co-simulation structure of ramming system

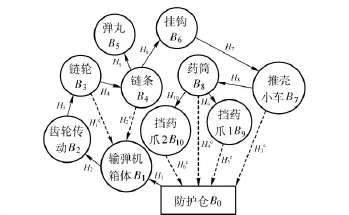
图2 供输弹系统拓扑结构Fig.2 Topological structure of ramming system

完成拓扑结构的定义后，MSC.Adams 应用带乘子的拉格朗日方法自动建立系统动力学方程并将碰撞铰以等效接触力形式引入方程，则供输弹系统的动力学方程可表示为

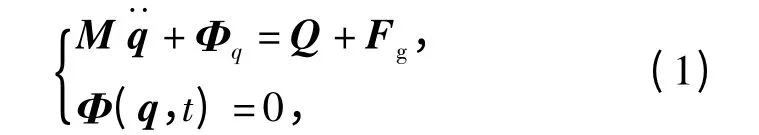
式中:q 为系统广义坐标列阵;M，Φq，Q 分别为系统的广义质量阵、约束方程Φ(q，t)=0 的雅克比阵及广义力阵;Fg为接触力F 相对于广义坐标q 的广义力列阵，采用基于impact 函数的实体碰撞接触模型［2］计算。

机械系统模型通过传感器和行程开关(借助MSC.Adams 的Sensor 和Measure 功能实现)反馈给控制模块(主要由逻辑判断模块组成，在MSC.Easy5中通过编写代码建立)，控制模块向液压系统电磁阀发出控制信号，以实现供输弹药系统的有序自动运行。

液压系统模型的建立是利用MSC.Easy5 提供的框图式建模环境，按照供输弹液压系统原理图通过调用液压元件库模型和编写非标准液压元件代码实现。求解时采用Adams 外部数据库［3］协同方式，将Easy5 中模型以一套GSE 方程形式加入Adams中(以动态链接库.dll 形式引入)，调用Adams/Solver，利用GSTIFF 积分器求解所有模型。

1.3 仿真结果及VV＆A 验证

图3为仿真得到的输弹过程链条头速度和位移曲线。往复推送式输弹链的啮合冲击及多边效应造成了系统动力学参数的周期性波动，由于耦合效应，这种周期性波动在液压系统中也较为明显。进行VV＆A 验证的常用方法［4］有:主观确认法、动态关联法和谱分析法等。但对于具体的仿真对象，进行验证最为有效的办法是用仿真结果与试验数据的一致性来对仿真模型的可信度进行评价。由于无相关实验测速数据，对供输弹系统动力学模型的验证只能以火炮出厂时进行的输弹、收链时间测试数据为依据。样本数据为从大量测试数据中随机抽取的，其中包含了随机参数的影响以及供输弹系统个体间差异、不同批次间的差异，具有很强的代表性。经统计处理，得到了输弹过程各动作的工作时间阈，如表1所示。从表中数据对比可以看到3 种装填角条件下仿真值均落在实验值区间内，说明仿真模型的计算结果是可信的。仿真模型计算时采用确定的设计参数，未考虑参数变化的随机性，其响应的计算值为确定值。

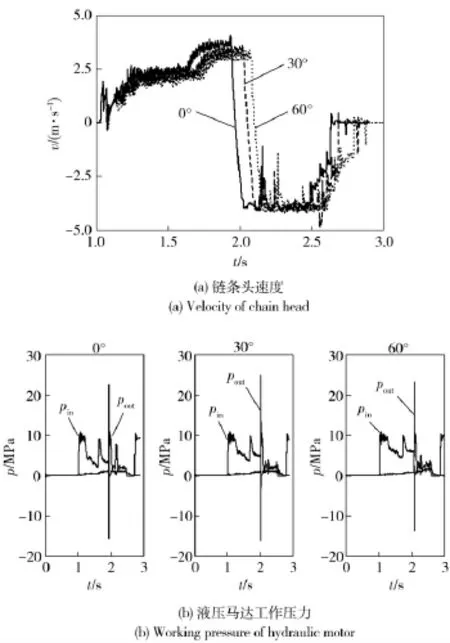
图3 仿真结果Fig.3 Simulation results

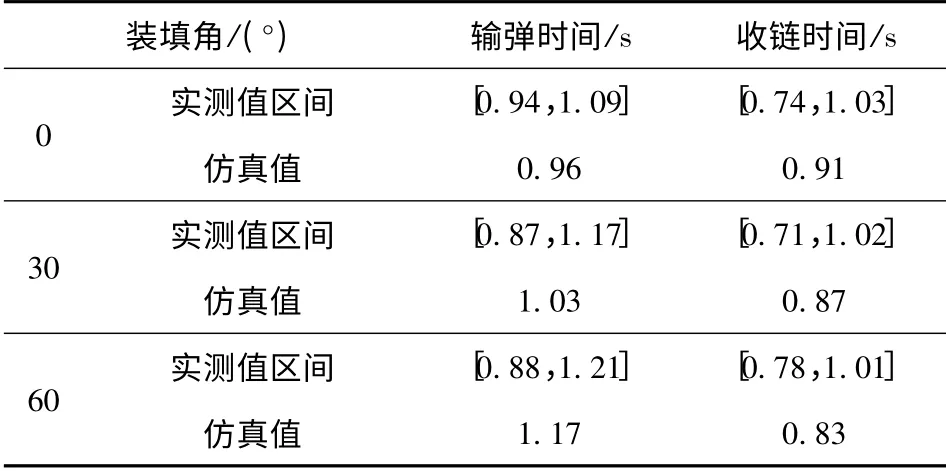
表1 数据对比Tab.1 Comparison of data

2 动力学随机响应VP-MCS-SVM 法

对于复杂结构的非线性随机动力学响应问题就目前的研究状况而言，最适合的方法是蒙特卡洛模拟法(MCS).然而，对于具有高可靠度的问题，想要得到精确的失效概率，所需要的计算量是非常巨大的，甚至是无法接受的［5］。对于供输弹机电液耦合系统，由于其刚体数目、自由度数目很大且存在大量接触，而且涉及多个系统间的相互耦合，仅一次确定性仿真计算就需要花费很长的机时(HP 9300 Workstation 8 G DDRII，MD Adams/Solver，GSTIFF 求解器求解需要3.0～3.5 h).运用MSC 方法求取机构动作可靠性时大样本量的要求无法满足。

因此，本文提出了VP-MCS-SVM 法，将虚拟样机(VP)仿真得到的小样本量的动力学仿真结果作为支持向量机(SVM)［6-7］的训练样本，通过训练在预测精度满足要求的情况下，再对大样本进行动力学响应预测。这能够有效发扬VP 和SVM 各自的优势，有效解决供输弹系统随机动力学求解效率和求解精度的矛盾，其求解流程如图4所示。

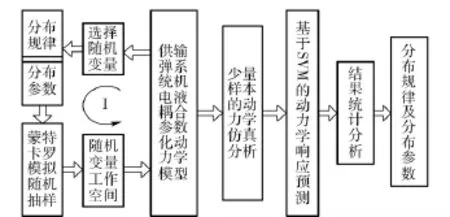
图4 供输弹系统随机动力学响应求解流程Fig.4 Solving process of ramming system's random dynamic responses

2.1 参数的随机性

在可靠性分析计算时通常将随机变量认为是服从理想分布，即其变量取值范围(-∞，+∞)或(0，+∞)，这显然不符合工程实际，而用两端截尾分布来描述工程实际中的随机变量则更为合理。各随机变量分布规律及其分布参数的确定最可靠的方式是针对具体参数进行专项实验，对所得大量数据进行统计处理，分析其分布规律，确定其分布参数。然而，在实际中上述方式很难办到，只能通过已有数据或类似的情况得到近似的分布特性及参数，也不乏分布规律难以确定的情况。而且还有一些随机因素不易进行试验，如对生产使用情况的估计、人的因素等，这时只能加入一些主观估计［8］。

表2为所研究的5 个随机参数的分布特征，均假设服从正态分布，分别为液压油温T(℃)、调压阀调定压力p(MPa)、大泵环形泄漏间隙hbp(mm)、小泵环形泄漏间隙hsp(mm)和马达环形泄漏间隙hmo(mm).

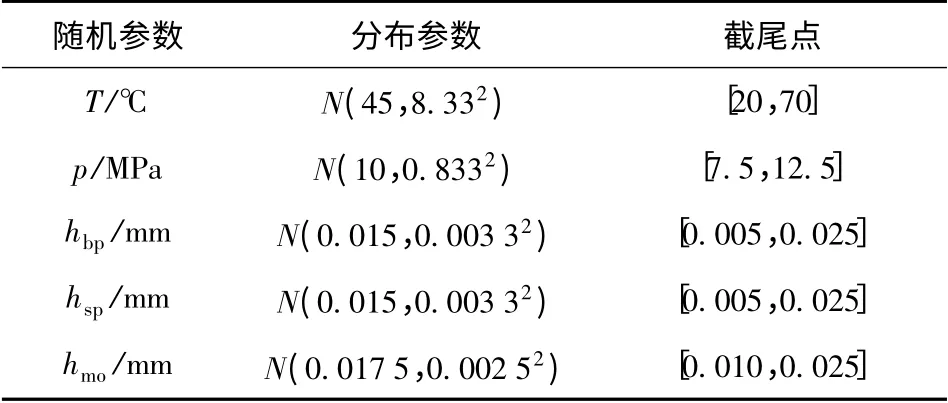
表2 随机参数分布特征Tab.2 Distribution characteristics of random parameters

2.2 动力学响应的随机性

由MCS 随机抽样产生100 个样本的试验空间，通过供输弹系统机电液耦合动力学模型进行100 次动力学求解，可以得到SVM 的训练样本。为清晰显示曲线簇的变化情况，图5和图6仅给出60°装填角条件下输弹过程随机动力学响应。

图5 链条头速度曲线簇Fig.5 Curve subgroup of chain head velocity

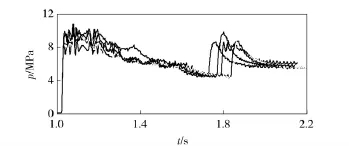
图6 系统压力曲线簇Fig.6 Curve subgroup of system pressure

从仿真结果来看，由于链传动固有的多边形效应和啮合冲击导致链条速度的周期性波动，同时引起液压系统压力和流量的波动，图中曲线的波动正是耦合作用的体现。

由于1 级输弹行程较长，所以hbp对输弹收链总时间影响较大;2 级输弹主要是提高输弹链卡膛点速度，所以hsm对输弹链卡膛点速度影响明显;hmo对两者都有显著影响。T 会影响液压油的密度、动力粘度等基本属性进而影响执行元件的泄漏量和粘性阻尼力，对输弹链卡膛点速度及输弹收链总时间有较大影响。p 对系统所能达到的最大工作压力有影响，主要体现在1 级、2 级输弹起始阶段，对两次加速过程有影响。从图中可以看出当考虑参数的随机性后，供输弹系统动力学表现出明显的随机性。

2.3 动力学响应预测

建立SVM 预测模型，将虚拟样机仿真得到的100 个样本中的90 个作为训练样本，10 个作为检验样本，预测相对误差最大为-1.03%.利用训练好的SVM 预测模型对由MCS 抽样所产生的容量为1 000 的试验空间进行动力学响应预测，并运用统计推断理论对其进行分析，如图7所示。

从图7可以看到，输弹链卡膛点速度vklt在正态分布概率试纸上概略成呈线性，并结合分布直方图可以初步确定其服从正态分布。分别按照正态分布、对数正态分布、威布尔分布应用K-S 检验法进行假设检验。通过对各种检验结果的分析和比较，发现vklt在α=1%显著水平下，只有假定其服从正态分布时才能通过K-S 检验。

对vklt进行参数估计可得:vklt～N (3.31，0.1492).截尾点可通过在随机变量极限状态下的确定性仿真得到:vklt∈［1.78，3.87］m/s.计算得正规化系数Kv=0.999 914 5，则其概率密度函数可表示为

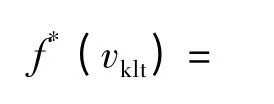
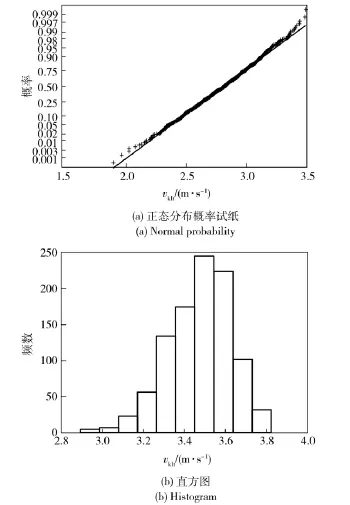
图7 卡膛点速度的分布Fig.7 Distribution of bayonet-chamber velocity

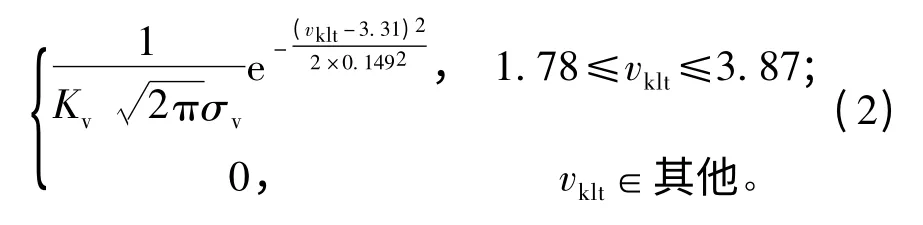
3 供输弹系统动作可靠性

机构动作可靠性是指机构在规定的使用条件下，在规定的使用时间内，精确、及时、协调地完成规定动作(运动)的能力，用概率表示就是机构动作可靠度。它强调了机构动作在几何空间中运动的精确度，在时间域内的精确性，以及机构间在几何空间、时间域上的协调性、同步性要求［8］。

3.1 动作可靠性模型

设机构由使用要求确定的性能输出参数为yk(k=1，2，3，…，s)，它是随机变量x1，x2，x3，…，xn的函数，故yk也是随机变量，有y =F(x1，x2，x3，…，xn).又设机构性能输出参数的允许极限值为Yk(k=1，2，3，…，s).当定义yk≤Yk事件为机构动作可靠时，则有

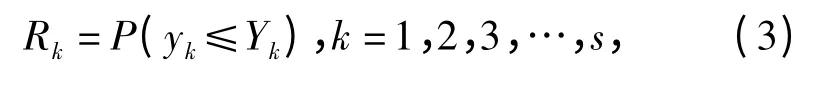
式中:Rk为机构第k 项性能输出参数达到规定要求的可靠度。

供输弹系统工作的主要参数指标为输弹链卡膛点最小速度要求vmin，klt和工作总时间ttot.当vmin，klt小于或ttot大于一定值之后判定系统出现功能故障，而实际上vmin，klt和ttot是相关的，并且系统对vmin，klt的要求是确定性的:vklt≥3.0 m/s.已知输弹链卡膛点速度服从两端截尾正态分布，则其可靠度为

3.2 考虑随机参数漂移时动作可靠度

考虑随机参数漂移主要基于2 点:1)随机参数的估计有一定偏差;2)随着服役时间变长，运转过程中的摩擦磨损等原因使得双联泵及马达性能劣化，即hbp、hsm和hmo三个随机变量的分布中心发生漂移，这一劣化过程是不可避免的，势必引起机构动作可靠度的降低。假设其分布形态不发生变化，只是分布均值发生漂移μ +Δμ，如图8所示。而T 和P 两随机参数的分布不变。

图8 分布参数的漂移Fig.8 Drift of distribution parameters

令Δμ 分别取2.5 μm 和5 μm，通过MCS-SVM方法可预测得到1 000 个样本空间的动力学响应，通过K-S 检验确定其仍服从正态分布。

1)Δμ=2.5 μm.vkt～N(3.24，0.2512)，vklt∈［1.435，3.80］m/s，正规化系数Kv=0.987 2.则动作可靠度为0.828.

2)Δμ =5.0 μm.vkt～N(3.08，0.2802)，vkt∈［0，3.73］m/s，正规化系数Kv=0.989 5.则动作可靠度为0.613 8.

图9为3 个随机参数均值漂移前后输弹链卡膛点速度的概率密度函数。从图中可以看出，在同样的随机环境和工作参数下，随着机构本身性能参数的劣化，系统响应的分布形式并没有发生变化，仍服从两端截尾正态分布，但分布均值减小、方差增大，供输弹系统的动作可靠度显著降低。

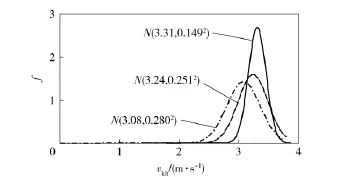
图9 卡膛速度的两端截尾概率密度Fig.9 PDF of two end truncated distribution of bayonet-chamber velocity

4 结论

本文采用基于软件接口的协同仿真策略，利用MSC.Adams 和Easy5 仿真平台对供输弹系统机电液耦合系统进行了动力学模型的构建和求解。由于目前在进行针对于仿真模型验证的专门实验上条件仍不具备，因而在进行VV＆A 验证时不能提供有力的数据佐证，这也是本文的一大缺憾。

针对利用MCS 法求解复杂结构系统随机动力学问题时计算量过于庞大的难点问题，提出了VPMCS-SVM 随机动力学求解方法，有效地解决了求解精度和求求解效率的矛盾。结合统计分析理论对供输弹系统的动作可靠性及随机参数漂移时的动作可靠度问题进行了研究。文章所采用的分析方法可为复杂系统的动力学分析和动作可靠性分析提供借鉴。

References)

［1］ 洪嘉振.计算多体系统动力学［M］.北京:高等教育出版社，1999.HONG Jia-zheng.Computational dynamics of multibody systems［M］.Beijing:High Education Press，1999.(in Chinese)

［2］ Msc Company.Adams/View user guide［DB/CD］.California:Msc Company，2005.

［3］ Msc Company.Thermal hydraulic systems library user guide［DB/CD］.California:Msc Company，2005

［4］ 康凤举.现代仿真技术与应用［M］.北京:国防工业出版社，2001.KANG Feng-ju.Technology and application of modern simulation［M］.Beijing:National Defense Industry Press，2001.(in Chinese)

［5］ Palaniappan R，Nam H K，Raphael T H.Inverse measure estimation for high reliability using low-number Monte Carlo simulations［C］∥11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference.Portsmouth:AIAA，2006.

［6］ 方瑞明.支持向量机理论及应用分析［M］.北京:中国电力出版社，2007.FANG Rui-ming.Support vector machine theory and application analysis［M］.Beijing:China Electric Power Press，2007.(in Chinese)

［7］ 邵秀丽，侯乐彩，黄海宽.基于SVM 和蒙特卡洛的滴丸含水量建模仿真［J］.南开大学学报:自然科学版，2009，42(5):57 -61.SHAO Xiu-li，HOU Le-cai，HUANG Hai-kuan.Modeling and simulation of pills moisture based on SVM and Monte Carlo［J］.Acta Scientiarum Naturalium Universitatis Nankaiensis:Natural Science Edition，2009，42(5):57 -61.(in Chinese)

［8］ 李良巧，顾唯明.机械可靠性设计与分析［M］.北京:国防工业出版社，1998.LI Lian-qiao，GU Wei-ming.Mechanical reliability design and analysis［M］.Beijing:National Defense Industry Press，1998.(in Chinese)