量化量测下约束方差滤波的容许量化水平研究

吴允刚，唐振民

(南京理工大学 计算机科学与技术学院，江苏 南京210094)

基于量化量测的估计是当前国内外的研究热点之一，得到了越来越多学者的关注。量化是指实际系统中把信号在幅度域上连续取值变换为幅度域上离散取值的过程，对传感器本身而言，量化水平即表征着仪器的分辨率。早期的研究工作可以追溯到1970年，Curry［1-2］、Clements［3］等提出了量化量测下基于最优条件均值估计的近似Kalman 滤波器，因该算法需要计算高维数值积分而限制了其应用。随着计算机性能的提高，2000～2005年间出现了大量的以文献［4 -7］为代表的通过近似数值计算方法来解决这一问题的成果。2007年，Moschitta［8］研究了量化量测下，克拉美-罗下界(CRLB)与量化间隔、测量误差之间的关系。Sun［9］研究了量化量测下传感器网络中能量约束下的参数优化问题。2008年，Djuric 等［10］给出了量化量测下无线传感器网络中的CRLB 计算公式。Duan 等［11］针对某典型的空中交通管制ATC 系统，基于UT 变换的思想研究了量化量测下最小均方误差(MMSE)意义下的状态估计问题。2010年，Zhou 等［12］研究了在量化量测下纯方位系统中的状态估计。Balkan 等［13］研究了量化量测下无线传感器网络参数优化问题，提出了通过加入适当的过程噪声来提高系统的最优估计性能。

上述学者的研究成果为进一步研究量化量测下的估计问题奠定了理论基础。目前，针对量化量测估计的研究大多集中于滤波器的设计、以及传感器网络的参数优化等问题，而对量化水平与估计误差之间的关系研究文献相对较少。如何设计一种估计算法能够在满足估计精度的前提下尽可能容许尽可能低的量化水平，是值得探讨的问题。误差协方差分配(ECA)理论为解决该问题提供了必要的理论基础。ECA 理论的核心思想是将给定的满足实际工程期望指标的滤波误差上界包含在稳态估计误差方差中。文献［14］研究了系统模型噪声一定时，在误差方差上界约束下，系统能够容许的最大量测强度噪声的满意滤波问题。

本文研究了量化量测下一种当前估计型稳态满意滤波器的设计问题。该滤波器在满足指定的估计误差方差上界约束下，容许系统有尽可能低的量化水平。其工程意义在于:在满足估计误差方差精度的前提下，确定尽可能低的量化水平，降低传感器的分辨率，从而可以相应降低传感器成本。

1 问题描述

量化量测下离散线性系统的数学模型

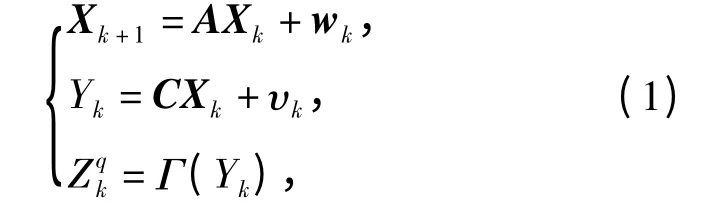
式中:Xk为n 维k 时刻的系统状态;Yk为量化前的测量值;Zqk为量化后的测量值，Zqk为标量;A 和C为适维矩阵且A 可逆;wk是n 维零均值方差为Q的高斯白噪声;υk是零均值方差为R 的高斯白噪声;Γ 为量化函数。

2 量化量测下当前型稳态滤波器及其性质

2.1 量化策略

采用文献［9］的量化策略。设传感器能够测量的幅值范围［U1，U2］，记U = U2- U1，量化水平lq(lq=2b，b 为比特位数)。可得到lq个量化点{aj∈［U1，U2］，j =1，2，…，lq}.U1=a1＜a2＜… ＜alq= U2，aj+1- aj= δ = U/(lq- 1).若Yk∈［aj，aj+1)，则对于Yk，P{Zqk=aj}=1 -p，P{Zqk=aj+1}=p，这里p=(Yk-aj)/δ.

若设量化误差εq=Zqk-Yk，则

故Zqk是Yk的无偏估计，且量化误差方差的上界为1/4δ2.

为方便问题讨论，假设εq是与υk不相关的白噪声，且用量化误差方差上界1/4δ2作为量化误差方差。记Rq=U2/4(lq-1)2.

故(1)式所描述的系统可改写成如下形式

2.2 量化策略下当前型稳态滤波器

对于(3)式所描述的系统，当前估计型稳态滤波器为

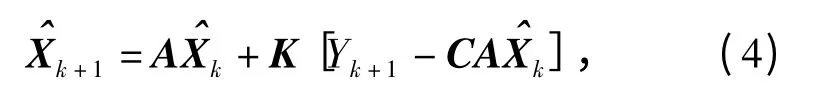
式中K 为待定定常滤波增益。估计误差系统Σe:

估计误差的协方差阵满足:

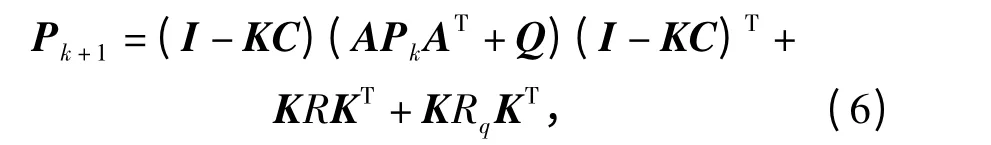
其相应的稳态误差协方差定义为

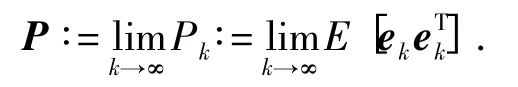
稳态误差协方差P 满足

下面首先讨论当前型稳态滤波器估计误差协方差阵P 的性质，定义函数

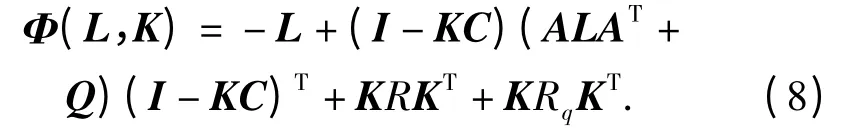
引理1［14］量化量测下，若存在滤波增益K 使误差系统Σe渐近稳定，当且仅当矩阵变量L 的不等式

有正定解，且若滤波增益K 使误差系统Σe渐近稳定，则相应的稳态协方差阵P 满足

式中，Ω(K)={L|Φ(L，K)＜0，L ＞0}.

根据文献［14］，由于(9)式是矩阵变量L 线性不等式，所以Ω(K)凸矩阵集，Ω(K)的下确界P 可以通过min{trace(L)|L∈Ω(K)}求得。

下面给出量化量测下，当前估计型稳态滤波方差与量化水平的关系。

定理1 量化量测下，当随机测量噪声R 固定时，误差系统Σe的当前估计型稳态滤波方差阵P是量化水平lq的单调递减函数，即若0 ＜lq1＜lq2，则P1≥P2，其中Pi(i=1，2)是相应于lqi(i =1，2)的稳态滤波方差阵。

证明1 记Pi相应的稳态滤波增益为Ki，i=1，2.则对P2和K2，有

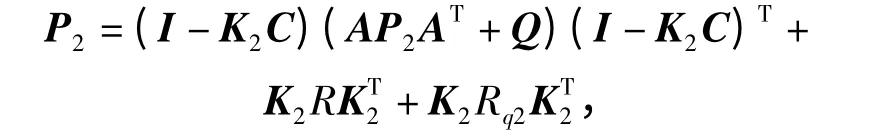
由于lq1＜lq2，所以

因此有

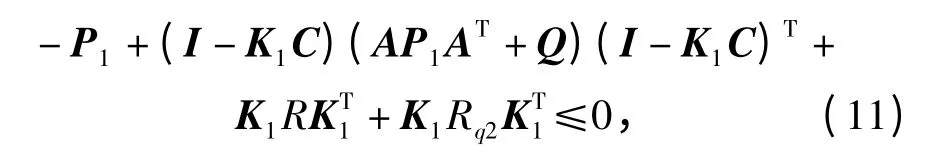
而P2是相应量化水平lq2的稳态滤波方差阵，由引理1 则对如下不等式的任意解(，K)

均有P2＜.若(11)式取等号，则P1为相应于量化水平为lq2的稳态滤波方差阵，由于稳态滤波方差阵的唯一性可知，P1=P2.若(11)式等号不成立，则(P1，K1)是Φ(，K)＜0 的一组解，因此P2＜P1.综上述，P1≥P2.

利用Schur 补分解定理可以给出定理1 的LMI形式。

定理2 若P，K 是系统(3)式的稳态滤波方差阵及滤波增益，则(P，K)是如下

LMI-1:

约束极大值问题max{trace(M)}的极值点。式中

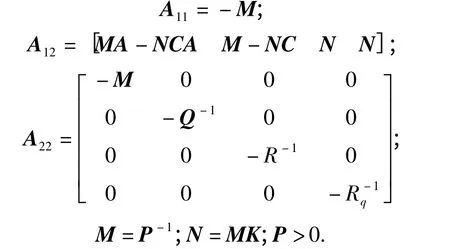
证明2 记M=P-1，N=MK，则Φ(P，K)＜0，P ＞0 等价于

由Schur 补引理可知，(13)式的矩阵不等式有解，等价于(12)式有解。由定理1 可知

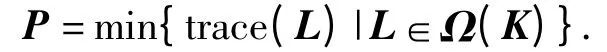
故(P，K)是max{trace(M)}的极值点。证毕。

3 误差方差约束下的容许量化水平

本节讨论当给定误差方差上界指标，即当diag(P)＜σ2(σ2为给定的方差上界常数)时，能够容许的最小量化水平。当在连续测量下(不经过量化处理)，即lq→+∞时(此时Rq→0)，考虑下列LMI 约束极大值问题。

LMI-2:

式中:

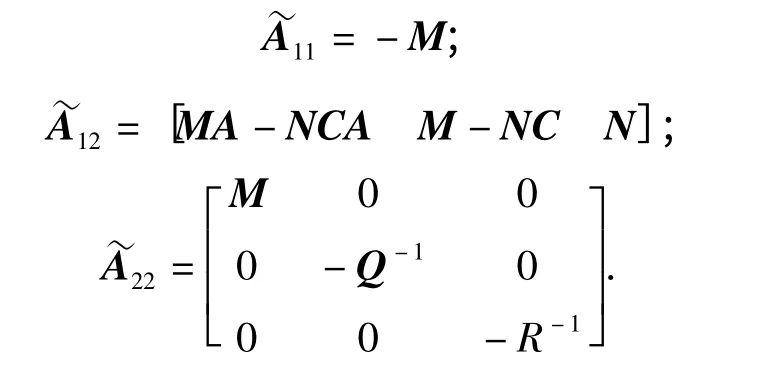
设M0是上面优化问题的最优解，则P0是稳态滤波的误差方差阵。对于满足diag(P0)＜σ2的方差上界指标σ2，在一定的量化水平下，总存在一种定常滤波增益，使滤波误差方差阵满足diag(P)＜σ2.由定理2 可知，要获得方差约束diag(P)＜σ2下滤波器能容许的最低量化水平，就应要求满足diag(P)＜σ2的所有滤波方差阵中非对角元素取尽可能大数值的矩阵。

下面给出量化量测误差方差约束下容许量化水平的滤波器设计方法。

LMI-3:

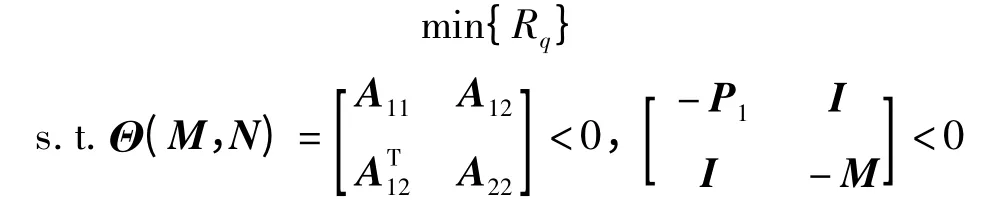
式中:P1与P0有相同的非对角元素，且diag(P1)=σ2.

记R*q为上述问题的最优解，则容许的量化的比特数和量化水平为

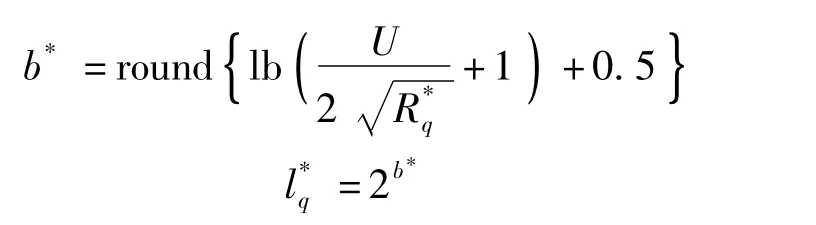
其中round{·}为取整函数。

算法流程图如图1所示。由于该算法每步都是求解凸优化问题，一般经几次循环便可获得满意的结果。

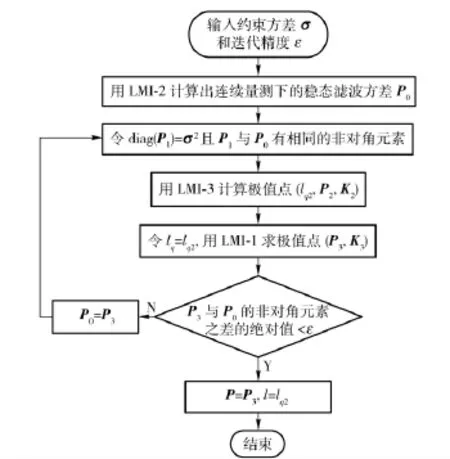
图1 误差方差约束下容许的量化水平算法流程Fig.1 Algorithm flowchart for allowable quantization level under constraint of error variance

4 算例

4.1 航空交通管制系统(ATC)

考虑一个典型的ATC 系统。从获取的目标高度的量化信息中估计目标的高度和上升/下降速度。设系统状态方程为

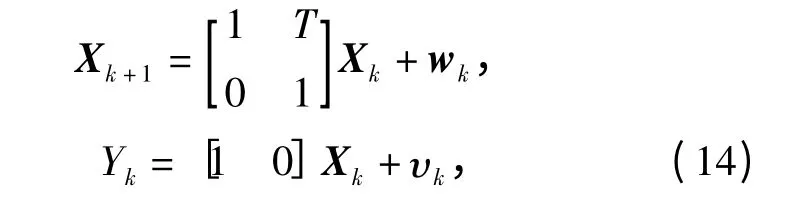
目标位置量化值为Zqk=Γ(Yk).

假设探测设备的探测范围为［50 m，10 000 m］，设一探测设备量化器的量化水平lq0=210.

wk是均值为0，方差的高斯白噪声。υk是均值为0，方差R =(50 m)2的高斯白噪声。

根据定理1 使用MATLAB-LMI 软件求出lq0=210时的稳态滤波误差方差阵和滤波增益

令lq0→∞，其余变量保持不变。求得连续量测下的稳态滤波误差方差阵及滤波增益:

为了做比较，选取滤波误差方差阵的上界指标为1.2，2，3，4，5，6，7，8 倍的对角元素，即σ2i=i ×diag{Pkal}，(i =1.2，2，3，4，5，6，7，8)，根据所设计的滤波方法，分别得到上述方差约束下的稳态滤波误差方差阵、增益和容许的量化水平。图2和图3分别为不同方差约束下的容许量化水平和比特位数。从图中可以看出，当方差约束指标增大时，系统容许的量化比特位数减小，能够降低传感器的分辨率，从而可以相应降低传感器成本。如当方差约束指标扩大为初始方差指标Pkal的8 倍时，容许的量化比特位数从10 位减少到5 位。表1为不同方差约束下的稳态滤波方差值，可以看出，文本给出的滤波器所得到的稳态滤波方差随着方差约束指标的增大而增大，并且满足相应的方差上界指标约束。

图2 不同方差约束下的容许量化水平Fig.2 Allowable quantization level corresponding to different constraints of variance

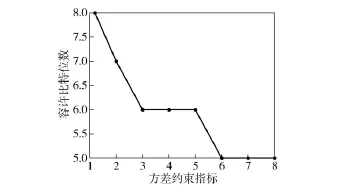
图3 不同方差约束下的容许比特位数Fig.3 Allowable quantization bits corresponding to different constraints of variance

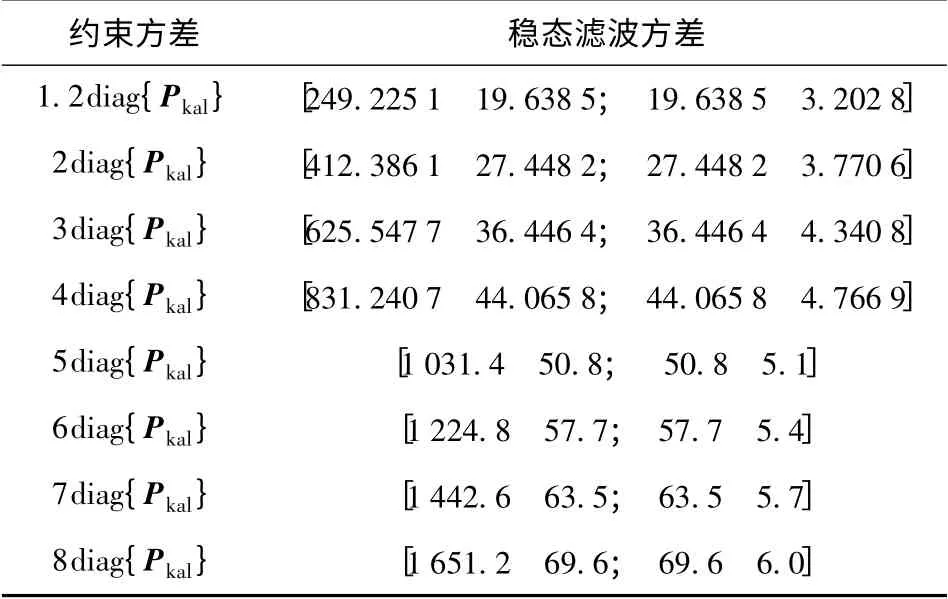
表1 不同方差约束下的稳态滤波方差Tab.1 Steady state error covariance corresponding to different constraints of variance

4.2 基于传感器网络的目标跟踪系统

考虑由10 个传感器构成的目标跟踪系统，目标的动态方程同(13)式，各传感器的测量方程为

各传感器测量误差方差为Ri∈［40 m2，90 m2］.可求出连续量测下稳态滤波误差协方差阵

表2为各传感器在不同方差约束下的容许量化比特位数，当方差约束指标增大时各传感器相应的容许量化比特位数减小。从表中可以发现，由于各传感器测量误差方差的差异，致使各传感器的容许量化比特位数并不相同。图4为不同方差约束下的位置滤波方差值，可以看出，位置估计误差方差在迭代20 步左右进入稳态值，同时该稳态值满足相应的方差上界指标约束。

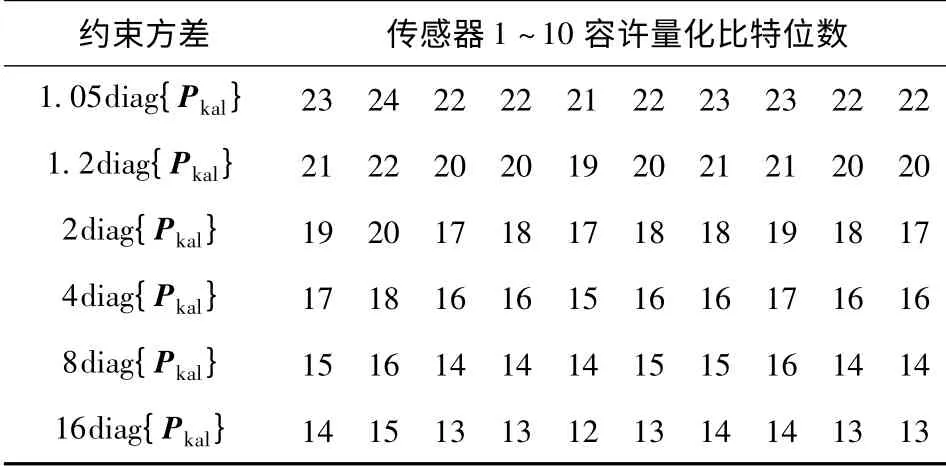
表2 不同方差约束下的容许量化比特位数Tab.2 Allowable bits of sensors corresponding to different constraints of variance

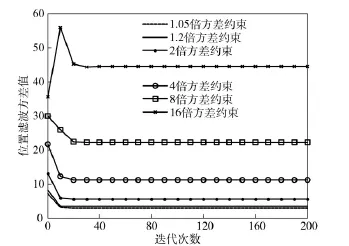
图4 不同方差约束下的位置估计误差方差Fig.4 Filtering error variance of altitude corresponding to different constraints of variance

由此可见，在滤波稳定下，当给定滤波误差方差阵的上界时，且探测器测量误差确定时，便可以得到容许的探测器量化水平的下界，从而给探测设备量化器的设计提供有益的参考。

5 结论

在实际工程中，由于技术和成本的制约，不可能无止境地提高系统的量化水平来提升传感器分辨率或选择高分辨率的传感器。探讨如何选取传感器的量化水平，具有重要的理论研究意义和工程应用价值。本文通过研究量化水平与当前估计型稳态滤波方差的关系，提出了一种在给定滤波误差方差阵的上界时计算所容许的量化水平下界的迭代算法。通过实例的数值仿真，验证了该算法的可行性。

References)

［1］ Curry R E.Estimation and control with quantized measurements［M］.Cambridge:MIT Press，1970.

［2］ Curry R，Velde W V，Potter J.Nonlinear estimation with quantized measurements-PCM，predictive quantization，and data compression［J］.IEEE Trans on Information Theory，1970，16(2):152 -161.

［3］ Clements K，Haddad R.Approximate estimation for systems with quantized data［J］.IEEE Trans on Automatic Control，1972，17(2):235 -239.

［4］ Sviestins E.Wigren T.Optimal recursive state estimation with quantized measurements［J］.IEEE Trans on Automatic Control，2000，45(4):762 -767.

［5］ Sviestins E，Wigren T.Nonlinear techniques for climb/descent rate estimation in ATC systems［J］.IEEE Trans on Control Systems Technology，2001，9(1):163 -174.

［6］ Ruan Y.Willett P Marrs A.Fusion of quantized measurements via particle filtering［C］∥Proc 2003 IEEE Aerospace Conference.IEEE:2003，4(4):1967 -1978.

［7］ Karlsson R，Gustafsson F.Filtering and estimation for quantized sensor information［R］.Sweden:Linkoping University，2005.

［8］ Moschitta A，Carbone P.Noise parameter estimation from quantized data［J］.IEEE Trans on Instrumentation and Measurement，2007，56(3):736 -742.

［9］ Sun S L，Lin J Y，Xie L H，et al.Quantized Kalman filtering［C］∥22nd IEEE International Symposium on Intelligent Control.IEEE:2007:7 -12.

［10］ Djuric P M Vemula M Bugallo M F.Target tracking by particle filtering in binary sensor networks［J］.IEEE Trans on Signal Process，2008，56(6):2229 -2238.

［11］ Duan Z S，Jilkov V P，Li X R.State estimation with quantized measurements:approximate MMSE approach［C］∥11th International Conference on Information Fusion.IEEE，2008:1 -6.

［12］ Zhou Y，Li J X，Wang D L.Posterior cramér-rao lower bounds for target tracking in sensor networks with quantized range-only measurements［J］.IEEE Trans on Signal Process Letters，2010，17(2):157 -160.

［13］ Balkan G O，Gezici S.CRLB based optimal noise enhanced parameter estimation using quantized observations［J］.IEEE Trans on Signal Process Letters，2010，17(5):477 -480.

［14］ 盛安冬，王远刚，戚国庆，等.满意滤波在航迹辨识中的应用［J］.自动化学报，2002，(4):559 -563.SHENG An-dong，WANG Yuan-gang，QI Guo-qing，et al.Appliction of satisfactory filtering to tracking identification problem［J］.Acta Automatica Sinica，2002，(4):559 -563.(in Chinese)