基于概率有限元法机床主轴可靠性分析
徐化文,杨林建
(四川工程职业技术学院,四川 德阳 618000)
对机械系统进行可靠性分析研究时,考虑到机械系统的“应力-强度”模型中输入、输出参数的不确定性,将概率分析和有限元分析结合起来,采用概率有限元法进行分析并确定主轴的可靠度。
不确定因素,是自然界中各事物的固有特性。在机械系统中,有许多的不确定性因素,如模糊性和随机性等。可靠性分析的根本原因。在于分析基本变量的不确定性:物理量的不确定性,统计方法的不确定性与分析模型的不确定性等等。
有限元分析法,是一种求解工程问题近似解的数值方法,广泛地应用于可靠性工程中。在有限元分析中,输入的参数常常是确定性的,如分析的结构形状和尺寸是确定的,施加的载荷是确定的,材料属性参数也是确定的,最后计算得出的结果(如应力、变形等)也是确定的。
然而,实际上所输入的参数,都存在着不确定性。输入参数的统计随机性,必然会对输出参数产生影响。研究表明,采用随机有限元法或概率有限元法,能很好地解决常规解决方式所带来的问题,主要为不确定性的输入参数对最终输出结果参数的影响方式和影响程度,而且不仅可以对现有的机械系统进行可靠性分析,确定其可靠度,而且可以对新设计的产品模型的可靠度进行验证分析,保证新产品满足一定的可靠度要求。
1 可靠性分析的基本过程
在进行可靠性分析中,其基本过程为:
结构的极限状态由功能函数Z=g(x)来表达,其中随即变量X=(X1,X2,…,Xn)表征各参数的不确定性。当g(x)>0,结构处于安全状态;当g(x)=0,表示结构处于极限状态;而当g(x)<0,则表示结构处于失效状态。
失效概率可表示为

式中,f(x)表示随机变量的联合概率密度函数,但是建立f(x)表达式对于较大部分的结构来说是比较困难的。
随着以数值模拟技术为基础的有限元理论和技术的发展,结合有限元法的概率有限元法或随机有限元法,能有效的用来进行结构可靠性分析和参数不确定性分析。在ANSYS中,主要采用响应面法和蒙特卡洛法来分析可靠性概率。
2 蒙特卡洛模拟法
蒙特卡洛模拟法是一种数值方法[3],主要通过随机变量的随机模拟或统计试验,来求解物理、数学和工程技术的问题近似解,因此也常被称为随机模拟法或统计试验法。
随着科技的发展,采用传统的数学方法或物理试验进行常规的计算处理,众多复杂的问题有时难以解决,而蒙特卡洛法则是解决这些难题的有效手段。
蒙特卡洛模拟的一般过程:
首先,构造一个简单适用的随机模型或概率模型,使问题的解和其中的随机变量的均值、概率、方差等某些特征相对应。
其次,根据概率模型的特点,使用适当的加速收敛方法,以提高其模拟精度。
再根据模型中随机变量的分布,产生随机数,实现一次随机模拟过程需要足够数量的随机数。
最后对模拟结果进行统计处理,给出问题的解和解的精度。
设结构功能函数Z=g(X1,…,Xn),式中Xi为具有任意分布的随机变量。对Xi(i=1,…,N)进行N次随机抽查,得到N组值(j=1,…,N)。将第j组(j=1,…,N)的值代入功能函数,得到N个Zj值(j=1,…,N)。设在N个Zj值中存在Nf个Zj<0,则结构的失效概率可以表示为

随着数值模拟技术的不断发展和完善,采用蒙特卡洛法与有限元法相结合的方式,能有效地解决与随机变量有关的工程实际问题。
对随机变量的数值模拟可概括如下:从整体中抽取简单样本做抽样试验。设X1,X2,…,Xn是n个独立的随机变量,来自同一个整体,假设他们分布的情况相同,且具有相同的有限均值和方差,用参数μ和σ2表示,则对于任意ε>0则有
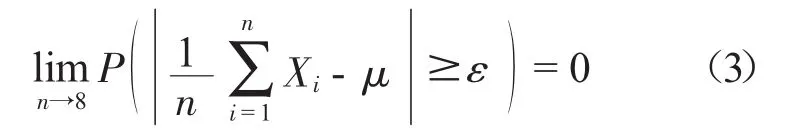
另外,假设随机事件A发生的概率用P(A)来表示,且在n次独立测试中,随机事件A发生次数为m,则频率用W(A)=m/n表示,则对于任意ε>0有

以上分析过程可总结为:有限元技术结合蒙特卡洛法来分析可靠性,就是进行N个循环,每进行一次循环,即将多一个随机变量在各自的分布函数范围内随机取值,将所得到的这些数值按有限元分析的步骤,即建模、网格划分并求解计算,其结果是变量的数值。然后对各个变量重复地进行随机取值,得到结果变量的N个数值,最后对随机变量和输出变量进行统计,确定其分布函数,敏感性等参数,进行可靠性分析。
蒙特卡洛法应用范围较广,其计算结果认为是可信的,前提条件是只要建模准确,模拟次数足够多。由于其他各种分析方法要求诸多假设,可能引入系统误差,而且在数学上实现很困难,所以,目前蒙特卡洛法是进行可靠性分析且检验结果较正确的唯一手段。
3 机床主轴实例分析[4~6]
机床主轴的力学模型如图1所示。
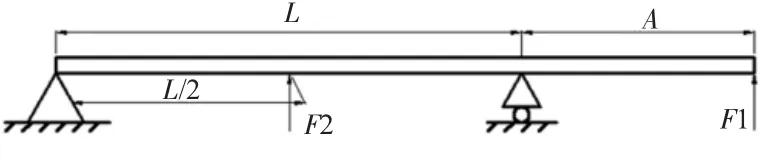
图1 机床主轴力学模型
相关数据列举如下:
F1=2 000±20 N;
F2=1 000±10N;
L=400 mm;
A=200 mm;
轴外径D1=80 mm,内径D2=40 mm;
轴端面的许用挠度Y=(0.000 1 0.000 2)L。
3.1 获得主轴各变量的分布函数
对于 F1、F2,按照“3σ”原则,
F1取μ=2 000 N,σ =20/3 N;
F2取μ=1 000 N,σ =10/3 N。
F1(μ1σ1)=(2 000,20/3)N,
F2(μ2σ2)=(1 000,10/3)N。
考虑加工误差和安装误差引起的相对位置误差,取L和A的变异因素为0.005,
L(μLσL)=(400,2)mm,
A(μAσA)=(200,1)mm。
轴材料的弹性模量也为随机变量,
E(μEσE)=(2.06×105,0.062×105)MPa。
3.2 建立仿真循环文件
在ANSYS10.0环境下,利用交互式界面或APDL语言进行仿真循环文件的建立。该文件的内容有:尺寸、载荷参数的确定,材料属性的确定,单元类型的确定,有限元几何模型的创建,单元网格的划分,施加载荷和边界条件进入求解器执行求解,进入通用后处理器作结果后处理,最终得到的变形图如图2所示,获得最大应力变形值UY_MAX,定义极限状态方程Z=Y-UY_MAX,定义概率分析文件名zhuzhoufenxi4.txt。
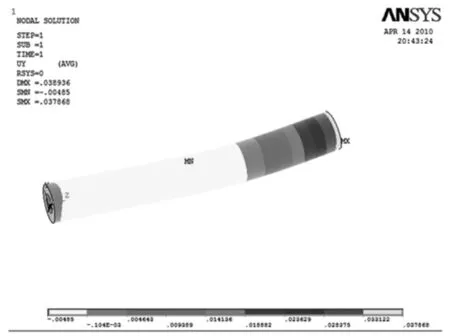
图2 主轴变形分析结果
3.3 进入概率分析模块执行PDS求解
在PDS中输入载荷、主轴尺寸、弹性模量的均值和标准差,定义Z和UY_MAX为随机输出变量,选择分析方法为蒙特卡洛模拟方法中的拉丁超立法,定义抽样次数500次,执行概率分析。
3.4 结果与分析
图3 UY_MAX样本趋势图表明曲线走势平稳,则说明仿真次数足够多。
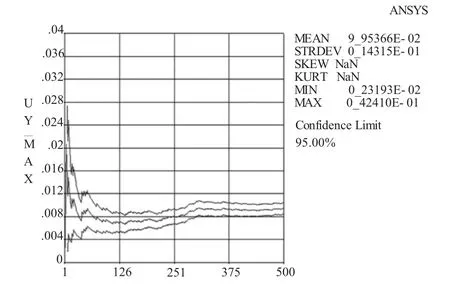
图3 UY_MAX样本趋势图
图4 为Z<0的可靠度计算结果。

图4 Z<0的可靠度计算结果
从图4可以看出,Z>0的概率是97.16%。由此可知该主轴的的最大挠度的可靠度为97.16%。
4 结束语
本文主要将概率分析与有限元分析相结合,采用概率有限元方法进行可靠性分析。由以上的分析结果得出,只要能够准确地获得机械模型变量的分布函数,就能够利用概率有限元的方法获得机械系统的可靠度。此方法方便快捷,有助于工程技术人员进行机械系统的可靠性设计、分析和预测。
[1]朱文予.机械概率设计与模糊设计[M].北京:高等教育出版社,2001.
[2]金伟娅,张康达.可靠性工程[M].北京:化学工业出版社,2005.
[3]杜 比,卫军明.蒙特卡洛方法在系统工程中的应用[M].西安:西安交通大学出版社,2007.
[4]叶 勇,郝艳华,张昌汉.基于ANSYS的结构可靠性分析[J].机械工程与自动化,2004(6):63-65.
[5]张胜民.基于有限元软件ANSYS7.0的结构分析[M].北京:清华大学出版社,2003.
[6]巫少龙.机械模糊可靠性优化设计研究[D].杭州:浙江工业大学机电学院,2004.

