新型旋转式压电惯性电机振子的冲击振动分析

邢继春，许立忠，王春光

(1.燕山大学 机械工程学院，河北 秦皇岛 066004;2.秦皇岛技师学院，河北 秦皇岛 066001)

基于压电效应的电机，称为压电电机。压电电机的种类型很多。除了各种类型的摩擦接触式超声电机外，还有非接触型超声电机、离合器耦合型压电电机、直线型表面波电机、真空型超声电机、冲击型压电电机等。此类电机在精密驱动领域已经发展为一种独特的驱动形式，例如超真空用精密位移装置、微型机器人手臂、扫描隧道显微镜等［1-2］。

新型旋转式压电惯性电机，是利用压电晶体的逆压电效应和惯性位移原理，用锯齿波作为激励电信号产生惯性冲击力驱动电机旋转［3］。与其它驱动方式相比，压电型惯性冲击驱动具有结构简单、能够在高速运动的同时实现长距离纳米级定位、容易实现多自由度驱动和不需要专用的位置保持装置等特点［4］。近年来国内外研究人员利用压电惯性冲击原理研制了一系列直线型和旋转型压电电机，并对该种电机的运动机理以及驱动信号和电机的结构参数对电机的性能的影响进行了阐述［5-7］。本文通过对电机核心部件振子的受迫冲击振动分析，进一步揭示此种电机的运动机理。

1 电机的结构设计

图1为旋转式惯性电机示意图。主要由振子、下轴、连接件、上轴、底座组成。其中惯性振子是由压电双晶体片、粘结剂、振子金属体构成。压电陶瓷片的尺寸10 mm×5 mm×0.5 mm，并且沿厚度方向极化。

图1 电机结构示意图Fig.1 The configuration of vibrator

2 激励信号

对惯性式旋转压电电机，激励方式非常重要。由于压电陶瓷片的容性负载特性比较突出，所以整个电机可以等效为一个容性负载。

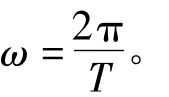
图2 激励信号的电压波形Fig.2 Applied electrical signal wave

在时域内，得到驱动电压为:

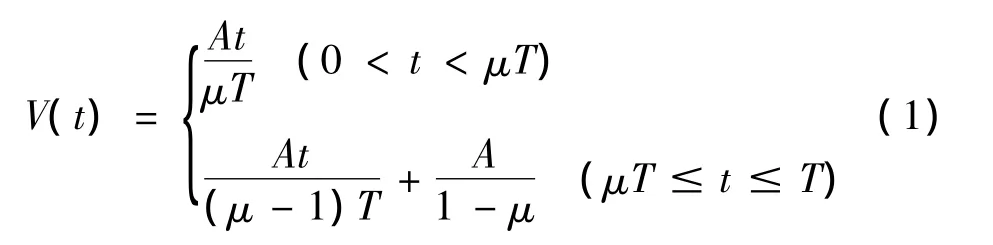
根据电容充放电原理，在激励电压信号处于上升沿时，压电陶瓷片两端电压响应为:

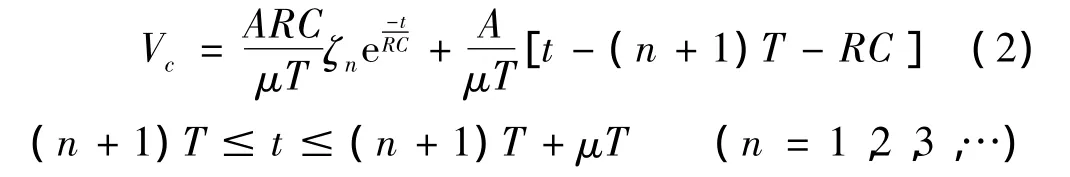
在激励电压信号处于下降沿时，压电陶瓷片两端电压响应为:

3 冲击受迫响应

如图3所示是旋转式压电惯性电机振子结构图。振子结构是由梁和环组合而成，利用梁—环面内弯曲原理计算梁的模态函数φn(x)。

由于压电陶瓷片厚度hp很薄，其每片平均电场为:

图3 简化的振子结构图Fig.3 The configuration of Simplified vibrator

根据振型叠加原理，梁弯曲振动位移可表示为:

此时的pzt元件只能贴在梁的上表面、下表面或上下表面。因此，pzt元件的应变为:

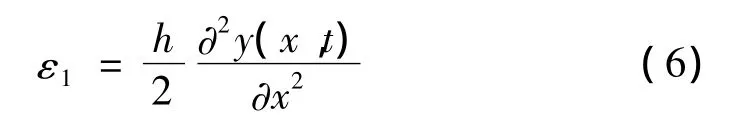
其中，h为梁的高度。

由第2类压电方程，可得到梁弯曲应力为:

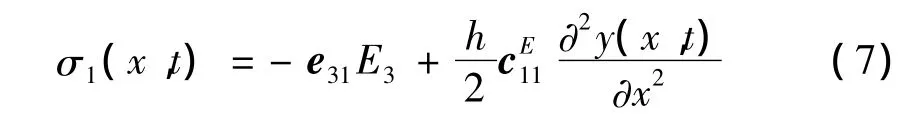
其中，e31为压电应力常数矩阵为机械刚度常数矩阵。分布的pzt元件应变能可写成:

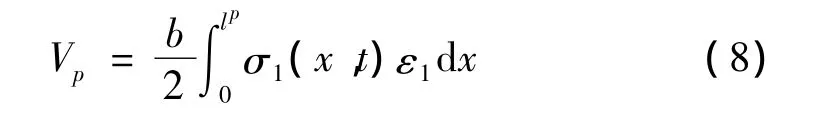
其中，b为pzt元件的宽度。另外，均匀梁(不含pzt元件)的应变能用下式表示:

梁在振动中的动能(含pzt元件):

其中，mij为梁的广义质量。

由于阻尼的存在，振子的耗散函数为:

其中，cij为梁的广义阻尼。

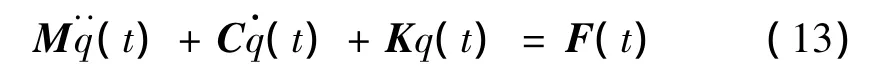
其中:M=［mij］为均匀梁的广义质量矩阵;C=［cij］为均匀梁的广义阻尼矩阵;K=［kij］为均匀梁广义刚度矩阵;F(t)为广义力列阵。

当利用位移振型正交性条件，可导出:

其中:Mj，Cj和Kj为均匀梁第j阶模态质量、模态阻尼、模态刚度，且模态力为用4片pzt来激振振子，压电片的长度为lp，宽度为b，厚度为hp，1，2片平均作用点为xa，3，4 片平均作用点为xb。

利用正交性导出广义力列阵为:

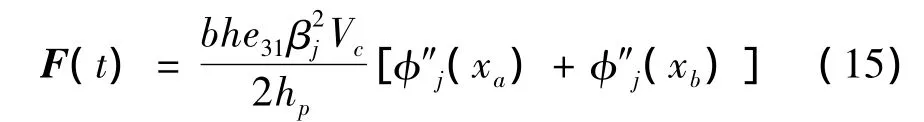
利用杜哈梅积分写出压电振子在激励信号下有阻尼受迫振动的通解为:

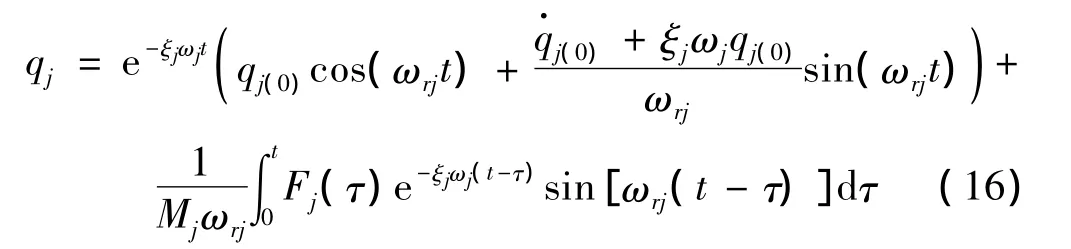
考虑阻尼的情况下，在激励电压信号处于上升沿时，振子的强迫响应为:

其中:

（1）夯实组织保障。为有效推进全市预算绩效管理，市人民政府成立了由市长任组长、常务副市长任副组长，市财政局等单位负责人为成员的预算绩效管理工作领导小组。

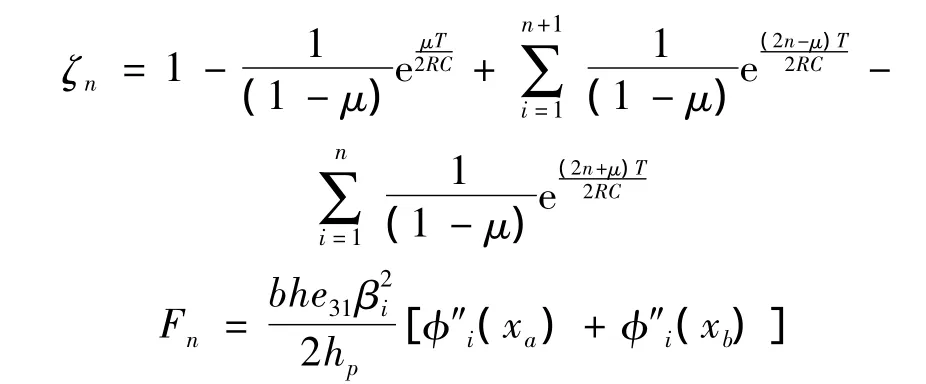
在激励电压信号处于下降沿时，振子的强迫响应为:

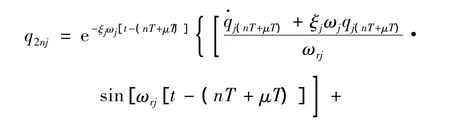
其中:

将式(17)、(18)代入式(5)得到压电振子梁位移响应为:

压电振子梁速度响应为

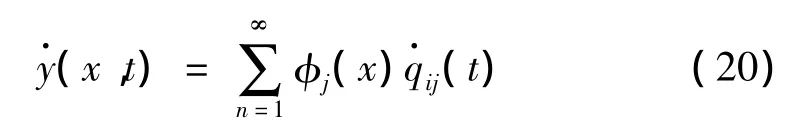
压电振子梁加速度响应为:

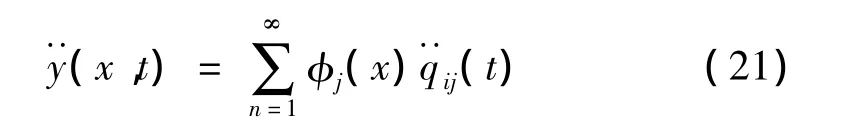
4 结果分析

4.1 压电陶瓷片两端电压分析

取旋转型惯性压电电机的驱动电压峰值为30 V，占空比μ=0.8，驱动电路电阻为100 Ω，单个压电陶瓷片的电容为2.4 nF。图4为在不同频率的锯齿波信号驱动下，电容两端电压的响应情况。结果表明:

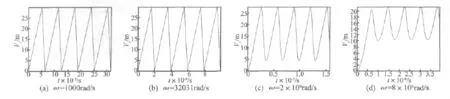
图4 在不同频率激励信号下压电陶瓷片两端电压Fig.4 The voltage of piezoelectric element under different frequency excitation signal

(1)压电振子在较低频率激励下，压电陶瓷片两端电压Vc的响应与激励信号波形基本相同，只是Vc的峰值略小于激励信号峰值30 V，为29.95 V。这是因为式(2)和式(3)中的指数项的值很小趋近0。

(2)压电振子在较高频率激励下，压电陶瓷片两端电压Vc的响应与激励信号波形不同，并且随着激励频率的增大Vc的峰值降低。随着激励信号频率的增大，Vc的波形也由锯齿波逐渐变为上升沿与下降沿对称的波形。

(3)由于旋转型惯性压电电机振子的工作模态为一阶固有频率32 031 rad/s，并且激励信号的频率低于其工作频率。选择低于其工作频率的激励信号时，压电陶瓷片两端电压Vc的响应与激励信号波形基本相同。

4.2 振子受迫振动分析

振子材料选用铜，系统参数如表1所示，取激励电压峰值A=30 V，研究压电振子梁端部在工作模态下的位移、速度与加速度响应(见图5)。图5表明:

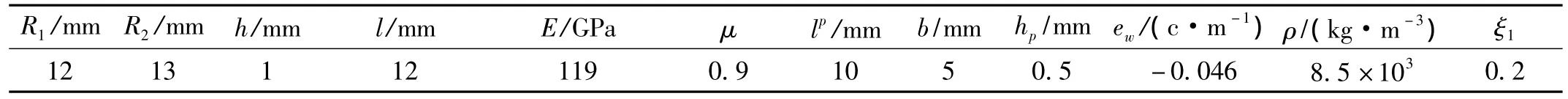
表1 振子参数Tab.1 The parameters of the vibrator

图5 振子位移、速度与加速度响应Fig.5 The displacement，velocity and acceleration of vibrator

(1)在频率较低ω≪ωj时，振子梁端部的响应波形与激励波形相似，由于阻尼的存在振子瞬态响应不显著。随着频率的增加，振子梁端部的响应波形由近似锯齿波变为近似正弦信号，振子的瞬态响应越来越显著。

(2)在频率较低ω≪ωj时，在激励信号上升沿和下降沿时间段的初始时刻瞬态速度响应随激励频率的增加显著。由于阻尼的存在，随时间推移，速度衰减一个恒值。随着频率增加，下降沿的时间变短，速度响应未能衰减至恒值。激励频率接近振子固有频率时，瞬态速度响应显著，速度响应波形逐渐趋于正弦波形，相位与位移信号相差90°。

(3)在频率较低ω≪ωj时，在激励信号上升沿和下降沿时间段的初始时刻瞬态加速度响应随激励频率的增加显著。由于阻尼的存在随时间推移，加速度衰减至0。随着频率增加，下降沿的时间变短，加速度响应未能衰减至0。激励频率接近振子固有频率时，瞬态响应显著，加速度响应波形逐渐趋于正弦波形，相位与位移信号相差180°。

4.3 旋转型惯性电机运动机理分析

旋转式压电惯性电机空载时轴承的摩擦力矩计算公式:

其中:f为滚动摩擦系数(0.001～0.015);d为轴承内径;F为轴承负载，即上轴、下轴、连接件、振子的重力。

旋转式压电惯性电机能够产生旋转的临界加速度a0，则有:

其中，Jr为振子环的转动惯量。

在一个周期内，振子系统梁端部位移响应和加速度响应如图6所示。

图7为振子振动分析示意图。假设振子由于激励信号突变所产生的惯性力矩M，以及惯性电机的最大静摩擦力矩Mc。如图6所示，将振子梁端部的加速度响应分为六个区域。在a，d，c，f区域为惯性力矩大于最大静摩擦力矩，在b，e区域为惯性力矩大于摩擦力矩。水平虚线为产生运动的临界加速度值。

惯性电机在一个周期所转过角度的大小，由其在该时间段内所获得和转动冲量矩的大小决定。也就是说在a区域由振子端部加速度响应曲线和上水平虚线所围成的面积与f区域振子端部加速度响应曲线和下水平虚线所围成的面积之差。若为正逆时针旋转，若为负顺时针旋转。

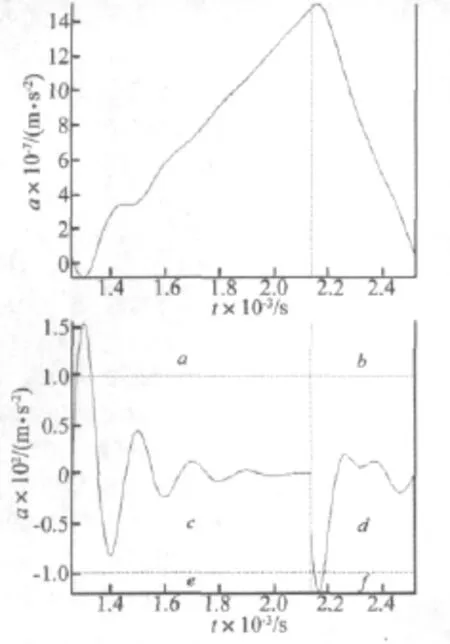
图6 振子梁端部位移和加速度响应Fig.6 The displacement and acceleration responses of the vibrator-beam end

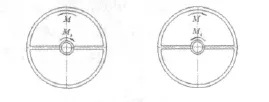
图7 振子运动分析图Fig.7 The analytical chart of Vibrator movement

为了更好的提高惯性电机的运行效果，根据旋转型惯性压电电机原理，可以尽可能的减小a，d区域面积，扩大c，f区域面积。同时，适当选择摩擦副也可以提高电机的驱动力矩。

4.4 激励信号的占空比对振子的影响

(1)在频率较低ω≪ωj时，压电振子梁端部的瞬态响应由于阻尼的存在得到充分衰减。上一周期下降沿的瞬态响应，对相邻周期上升沿的影响较小。上升沿对应的振子端部瞬态响应不明显。激励信号的占空比为μ=0.1～0.9区间时，由于上升沿和下降沿的突变所产生的惯性力矩较小，驱动力矩M小于静摩擦力矩Mc，电机处于静止状态。如果改变占空比，使其处于0＜μ＜0.1区间，则上升沿斜率增加获得较大惯性力矩(大于最大静摩擦力矩)，惯性电机转子出现逆时针旋转。而在0.9＜μ＜1区间，下降沿斜率增加获得较大惯性力矩(大于最大静摩擦力)，惯性电机转子出现顺时针旋转。

(2)为了获得较大的驱动力矩，应该尽可能的减小a区域面积，扩大f区域面积，有利于电机轴顺时针旋转。在激励信号占空比μ=0.5时，a区域面积最小。这是因为激励信号的上升沿和下降沿时间相等，压电振子梁端部的瞬态响应由于阻尼的存在得到充分衰减。并且激励信号上升沿和下降沿的斜率变小，压电陶瓷片电压变化变缓，压电振子惯性力矩减小。

(3) 当激励信号频率接近压电振子工作模态的固有频率。压电振子端部位移响应和加速响应幅值明显增大。在一个周期内，a，d和c，f超出虚线区域的面积基本相等，电机轴发生左右往复旋转。在不同激励信号占空比情况下，差别不大。

4.5 振子参数改变对电机运行的影响

振子产生的加速度响应曲线与临界加速度a0(水平虚线)所围成的面积可以反映惯性冲击力矩的大小，该面积为;

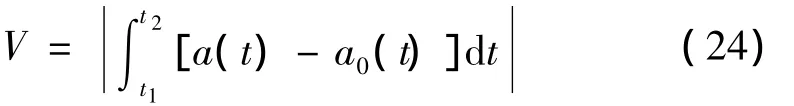
振子材料选用铜，上轴和下轴选用铝，连接件选用绝缘塑胶材料。取激励电压峰值A=30 V，激励锯齿波信号频率为4×103rad/s。其它系统参数如表1所示，改变振子外环半径R2，计算V值如表2所示。改变振子梁长l，振子环外半径和内半径差保持1 mm，计算V值见表3。改变振子梁高h，计算V值见表4。从表2～表4可知:

(1)随着振子环外半径R2的增加，临界加速度a0逐渐降低，而V值逐渐增大。

(2)随着振子梁长l的增加，临界加速度a0逐渐降低，同时V值逐渐减小。

(3)随着振子梁厚h的增加，临界加速度a0逐渐增大，同时V值逐渐减小。

由此可知，增大振子环外半径R2、减小振子梁厚h和振子梁长l，可以增加振子的惯性冲击力矩。

表2 不同R2下的a0和V值Tab.2 The value ofa0andV under differentR2

表3 不同l下的a0和V值Tab.3 The value ofa0andV under differentl

表4 不同h下的a0和V值Tab.4 The value ofa0andV under differenth

5 结论

本文根据电容充放电原理，推导了压电陶瓷片两端电压响应公式，并利用杜哈梅积分推导出压电振子在激励信号下阻尼受迫响应公式。运用动力学方法分析了旋转型惯性电机运动机理，可以通过减小a，d区域面积，扩大c，f区域面积以及适当选择摩擦副提高电机的驱动力矩。研究了激励信号的占空比对振子冲击力矩的影响规律，以及振子参数对振子冲击力矩的影响规律。结果表明，增大振子环外半径R2、减小振子梁厚h和振子梁长l，可以增加振子的惯性冲击力矩。这些研究工作为旋转式压电惯性电机的设计与控制奠定了理论基础。

［1］赵淳生.超声波电机设计与应用［M］.北京:科学出版社，2007.［2］温建明，程光明，曾 平，等.新型惯性式压电旋转驱动器［J］.吉林大学学报，2007，37(5):1112-1115.

［3］陈西平.压电型惯性冲击式运动机构驱动理论和试验研究［D］.长春:吉林大学，2003.

［4］ Liu Y T，Higuchi T，Fung R F.A novel precision positioning table utilizing impact force of spring-mounted piezoelectric actuator-part II: theoretical analysis［J］. Precision Engineering，2003，27(1):22-31.

［5］陈西平，付 庄，曹其新，等.压电型惯性冲击机构的驱动波形分析［J］.压电与声光，2005，27(3):316-319.

［6］Yoshida R，Okamoto Y，Okada H.Development of smooth impact drive mechanism(2nd report)［J］.J.Jpn.Soc.Precision Eng，2002，68(4):535-541.

［7］邢继春，许立忠，梁永丽.旋转式惯性压电电机的振子模型研究［J］.振动与冲击，2010，29(11):105-109.

［8］Kim S C，Kim S H.A precision linear actuator using piezoelectrically driven friction force［J］.Mechatronics，2001，118:969-985.