基于时序分析的拉伸件成型裂纹的特征参数提取

骆志高，叶红英，胥爱成

（江苏大学 机械工程学院，江苏 镇江 212013）

在薄板成型过程中，变形程度、受力情况以及摩擦与润滑等情况千差万别，制件在成型过程中产生裂纹在所难免，而当裂纹扩展到一定程度则可能造成经济损失亦或灾难性的事故。因此，从经过处理的声发射信号中提取到相关的特征参数，成为本研究的主要目的。

近年来，在声发射信号特征参数提取方面国内外均取得了相当的成果。Khamedi等［1］采用小波技术研究了不同马氏体含量的双相钢在拉伸试验中产生的声发射信号能量基本上集中在两个或三个不同组成部分的频率范围，每个频率范围与单独的微观故障结构相关。Chen等［2］采用声发射技术对磨削烧伤与振动进行了分析，采用小波包分解与短时傅里叶变换对声发射信号进行预处理并分解至不同频段，得到了较好研究成果。Mohanty等［3］采用高斯时间序列模型对金属结构进行寿命预测，结果表明与其他组合方法相比，采用高斯时间序列模型的预测误差要小得多。何正嘉等［4］采用第二代小波变换对数控机床铣削过程产生的声发射信号进行分析，最终有效地提取并识别出立铣刀破损状态特征以及对工件表面加工质量的影响，为故障诊断、误差溯源、质量控制提供了科学的依据。吴小俊［5］对焊接裂纹声发射监测系统进行了软、硬件设计，并开发了一套基于虚拟仪器技术的焊接裂纹声发射监测分析系统平台。成建国［6］采用神经网络模式识别法对混流式水轮机转轮产生裂纹时的声发射信号进行识别，并通过所设计的特征提取器提取出五个特征参数，从而成功识别出金属裂纹声发射信号。

本文将声发射技术应用在对金属拉伸件的成形质量进行实时在线检测尚处于萌芽阶段，同时由于该类型信号的样本采集及特征识别比较困难等特点，若能发现裂纹产生的声发射信号并对其进行识别，则对于金属板料加工有重要意义，所以对其研究具有很高的学术价值和经济价值。同时，本文在采用小波包技术与时序分析相结合的方法提取反映制件裂纹特征参数的准确性方面取得了较大的提高。本文选取ST14材料盒形拉伸成型件为研究对象，研究板材在深拉伸状态下裂纹声发射信号特征参数的提取。采用时序分析和MATLAB相结合，从经过小波包分解的声发射信号中提取出相关的特征参数。

1 时间序列分析

1.1 时间序列分析概论

时间序列是一种处理动态数据的参数化时域分析方法。其主要手段是选择恰当的数学模型来近似描述动态数据，通过研究分析，更本质地了解数据的内在结构和复杂特性，以达到控制和预报的目的［7］。本研究中的声发射信号是将已经小波包分解后的平稳信号通过时间序列分析来提取其特征参数，从而使提取到的特征参数值更加的精确。由于声发射传感器的频率带宽为100～300 kHz，故采集的信号为高频信号，因此可以忽略其他复杂信号。

1.2 时间序列模型类型的选择

时间序列模型一般分为三种：ARMA（n，m）模型、AR（n）模型和MA（m）模型。一般来说，AR模型与ARMA模型的自相关函数ρk具有拖尾特性，MA模型的ρk具有截尾特性；而MA模型与ARMA模型的偏自相关函数具有拖尾性质，AR模型的偏自相关函数具有截尾性质。因此，可根据需要建模的时序数据的自相关函数与偏自相关函数的性质进行建模类型的选择［8］。

1.3 时间序列模型定阶准则

FPE准则（最小最终预报误差准则）是由样本对模型定阶。它是以模型输出的一步预报误差方差来判定模型阶次：一步预报误差方差阵的行列式越小，就认为模型拟合得越理想，这时的模型阶次认为是最佳的阶次，即FPE（n）最小的n值作为模型的最佳阶数。

1.4 时间序列模型参数的估计

模型参数估计是建立时间序列模型必不可少的重要内容，常用的方法分为两类：AR模型的参数估计方法分为两类：一类称为直接估计法，包括最小二乘估计法、自相关法（即解Yule-Clayton方程估计法）等；另一类称为递推估计法，包括矩阵递推估计法、参数递推估计法、实时递推估计法等［9］。在本研究中，主要采用最小二乘估计法来进行模型参数的估计。

2 MATLAB在特征参数提取中的应用

Matlab是Math Work公司于1984年推出的功能强大的大型工程软件，其科学计算功能的强大和开放式的开发思想使其成为当今最为流行的、最为优秀的科技应用软件之一，在数值分析、科学计算、算法开发、建模和仿真等方面具有独特的优势。特别是在一些常用的复杂的矩阵运算以及仿真运算上，Matlab充分体现了其优越［10］。

将声发射原始信号进行数据处理并检验合格后，在MATLAB软件中计算各数据的自相关系数与偏相关系数，确定模型类型，图1和图2是一组分解信号的自相关系数与偏相关系数连线图。

由图可知：该组信号的偏自相关系数具有明显的截尾特性，而自相关系数则是拖尾特性，所以该组信号的时序模型确定为模型。同理，可确定其他各组信号的时序模型。根据检验结果，所有分解信号都满足建立模型的条件。

对8组分解信号采用FPE准则确定模型的最佳阶次。在MATLAB软件中的命令为：

按上述程序生成各分解信号的FPE分布线图，并求取与各分解信号最小FPE值对应的阶数。

根据软件计算所得最佳阶数分别对各组信号进行时序建模，得到各组信号的自回归模型。对于AR模型的参数估计，MATLAB中采用 ar函数，具体调用格式为：

其中，y为需要建模的时间序列信号，n为模型阶数，＇approach＇表示采用的参数估计方法，包括向前反馈法、最小二乘法、Yule-Walker法、Burg法等。本研究采用最小二乘法估计模型参数。

经检验，模型残差符合正态分布，说明所建立的时序模型是正确的。

最后采用E=trapz（f0，px0）命令提取时序谱能量值作为反映裂纹信号的特征参数。

3 金属拉伸制件声发射信号数据分析

3.1 测试方法

3.1.1 实验过程

本实验对金属板料ST14（尺寸为400×600×1.5 mm）在拉伸模具上进行拉伸试验。在板料拉伸成型之前，需将板料放置压边圈的中间位置，故需要将在板料上标出其对称线，方便放置于压边圈中央。在拉伸过程中，板料始终与卸料板相接触，故将声发射传感器分别置于卸料板的周围，并用声发射仪采集全过程声发射信号。

本研究的主要实验步骤如下：

（1）根据模具尺寸裁剪板料，并对板料进行标定；标定目的是在数据采集时，将板料放置在凸模的正中间位置；

（2）将声发射传感器安装在板料上，测定断铅信号，以判定声发射检测设备的完整性；

（3）根据模具结构及制件裂纹可能产生的位置，安装声发射检测设备；并在声发射传感器所在零部件上进行断铅信号测定，以确保声发射检测设备可以采集到声发射信号；

（4）对液压机的运行速度、模具压边力等参数进行调整，确保制件产生不明显的小裂纹以及不产生明显裂纹；

（5）对采集到的信号进行分析处理和裂纹信号的识别。

3.1.2 实验参数的设置

（1）声发射传感器的选择及参数设置

针对金属裂纹产生的声发射信号的特点，选取鹏翔科技的PXR15谐振式声发射传感器，其主要性能参数为：频率带宽：100～300 kHz，灵敏度＞65 dB，谐振频率：150 kHz，使用温度范围：-20～80℃，尺寸：φ18×17 mm。

（2）前置放大器的选择及参数设置

本次实验采用PXPAIV前置放大器，其优点是高带宽、抗冲击、体积小、低噪音以及较高的兼容性，其主要性能参数为：

频率带宽：15 kHz～1.5 MHz，增益：34/40 dB，噪声：2.8 μVRMS，使用温度范围：-30 ～ 80℃，电源功耗：28 V/30 mA，主要尺寸：90×35×30 mm。

（3）声发射采集卡的选择及参数设置

本次实验采用的是PXDAQ12254型号声发射卡，集成在数据处理系统中，其主要性能参数为：

声发射输入通道数：4通道/卡，输入电阻：40 Ω，信号带宽：5 kHz～4 MHz，采样分辨率：12字节，采样速度：20 MSps/S，噪声最小阀值：28 dB，最大信号幅度：100 dB，通道隔离度：≥90 dB。

3.2 实验数据处理

3.2.1 数据采集

在金属中，裂纹产生的频率可达100 kHz以上，为增大信号的分辨率，设定采样频率为1 000 kHz。图3和图4是分别是有明显裂纹与无明显裂纹的声发射信号图。

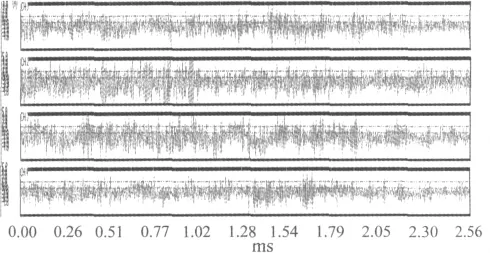
图3 制件有明显裂纹声发射信号图Fig.3 Parts of AE signals with significant crack

3.2.2 数据处理

本研究将处理过的2组声发射信号S1，S2分别导入到MATLAB软件中，通过时序分析得到各分解信号的自回归谱，如下图5和图6所示：

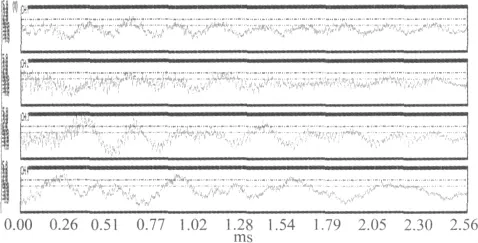
图4 制件无明显裂纹声发射信号图Fig.4 Parts of AE signals with no significant crack

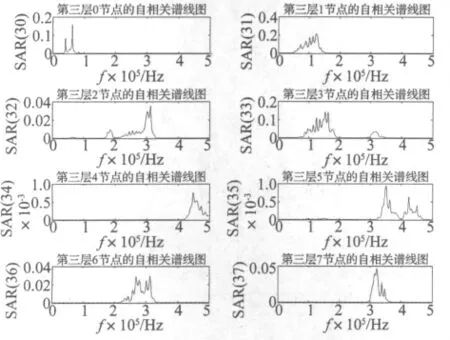
图5 信号S1的各分解频带时序谱值图Fig.5 The timing spectrum value figure of each decomposed band for the signal S1

3.2.3 能量参数的提取

由于大多数金属都具有一定的塑性，裂纹向前扩展一步，则将积蓄的能量释放出来，而裂纹尖端区域卸载。这样，裂纹扩展产生的声发射很可能比裂纹形成的声发射还大得多。故声发射信号的能量值对裂纹特征十分敏感。

为直观的将声发射信号的能量分布从频率由高到低显示，将声发射信号S1，S2各通道的时序谱能量值连成平滑的曲线，如图7、图8所示：

图6 信号S2的各分解频带时序谱值图Fig.6 The timing spectrum value figure of each decomposed band for the signal S2

3.3 实验结果分析

从有裂纹信号的各频带能量分布图（图7）与无裂纹信号的各频带能量分布图（图8）可以看出这两种信号的明显区别为：

（1）有裂纹声发射信号各分解频带能量值之和远大于无裂纹声发射信号能量值；而且自125 kHz到300 kHz频段，各分解频段的能量值都比无裂纹声发射信号的大很多；

（2）有裂纹声发射信号能量分布是先增大后减小趋势；而无裂纹声发射信号能量分布是渐减小的趋势；

（3）有裂纹声发射信号与无裂纹声发射信号的第一分解频带的能量值百分数呈现相反的比例趋势，很明显：有裂纹声发射信号的第一分解频带的时序谱值占整段信号时序谱值的比值较小，而无裂纹声发射信号的第一分解频带的时序谱值占整段信号时序谱值的比值较大；同理，这两组分解信号的第三分解频段的时序谱值呈现相同的规律，不同的是有裂纹声发射信号所占比值较大，而无裂纹声发射信号所占比值较小。

4 结论

根据金属拉伸制件在成型过程中产生的声发射信号特点，对经过小波包分解的声发射信号进行时序分析和MATLAB处理，成功的得到了各信号的自回归谱图。同时，为直观的将声发射信号的能量分布从频率由高到低显示，将声发射信号各通道的时序谱能量值连成平滑的曲线，从而得到了声发射信号的能量分布图。这为判断成型制件的质量提供了有利的依据。

［1］ Khamedi R，Fallahi A，Oskouei A R.Effect of martensite phase volume fraction on acoustic emission signals using wavelet packet analysis during tensile loading of dual phase steels［J］.Materials and Design，2010，31：2752-2759.

［2］ Chen X，Griffin J.Grinding burn and chatter classification using genetic programming［J］.Source：Key Engineering Materials，2009，389-390：90-95.

［3］ Mohanty S，Das S，Chattopadhyay A，et al.Gaussian process time series model for life prognosis of metallic structures［J］.Journal of Inteuigent Material Systems and Stvuctures，2009，20（8）：887-896.

［4］何正嘉，曹宏瑞，李 臻，等.铣削刀具破损检测的第二代小波变换原理［J］.中国科学 E辑：技术科学，2009，39（6）：1174-1184.

［5］吴小俊.声发射技术在焊接裂纹检测中的应用研究［D］.重庆：重庆大学，2008.

［6］成建国.金属裂纹声发射信号识别及报警的方法研究［D］.广西：广西大学，2008.

［7］尹光志，岳 顺，钟 焘，等.基于ARMA模型的隧道位移时间序列分析［J］.岩土力学，2009，30（9）：2727-2732.

［8］王振龙，胡永宏.应用时间序列分析［M］.北京：科学出版社，2007.

［9］任 欣，万新南.基于MATLAB的AR及BP模型在矿井涌水量预测中的应用与比较［J］.煤炭技术，2009，28（3）：64-66.

［10］杜欣慧，张丽芳，李 青，等.电力系统负荷预测软件中VB与Matlab的接口方法研究［J］.电力系统保护与控制，2010，38（19）：208-211.