基于改进智能算法的非线性转子系统的参数辨识

韩 放，郭杏林，高海洋

（大连理工大学 工业装备结构分析国家重点实验室，大连 116023）

确定转子系统的未知参数是一项非常复杂的工作，对于具有非线性刚度和碰摩特性的转子系统来说，由于碰摩力的间断性使得参数的识别变得更加的困难。目前，优化算法越来越多的用来求解机械系统的反问题当中［1］，从而也为参数识别提供了一个有效的替代方法［2］。近年来，人们从仿生学的机理中受到启发，提出了许多用于求解优化问题的智能方法，如模拟退火算法［3］、遗传算法［4］、蚁群算法［5］等，虽然在求解中不需要任何的梯度信息，但由于智能算法是一种基于全局的优化算法，因此时间消耗比较大，为了能够降低搜索时间提高搜索能力，许多学者提出了改进方法，如局部搜索算法与遗传算法相结合的提高算法［6-7］，GASA算法［8］，GA 与 AA 的混合算法［9］，融合粒子群和局部搜索的优化算法［10］，遗传算法与神经网络的混合算法［11］等。

本文在多种智能算法的启发下，试图探寻一种较好的平衡方法。在对多种经典算法进行研究和对比后，设计了一种改进遗传蚁群算法（GAAC）与局部邻域搜索（local Neighborhood-searching，LNeS）相结合的新算法（Ne-GAAC）。以考虑非线性刚度和碰摩特性的单盘转子模型为对象进行仿真分析，讨论了Ne-GAAC方法在识别非线性转子系统若干参数的有效性和可行性。

1 遗传算法与蚁群算法的融合

遗传算法（Genetic Algorithm，GA）具有快速全局搜索能力，但对于系统中的反馈信息没有利用，往往导致无为的冗余迭代，求解效率低。蚁群算法（Ant Colony Algorithm，ACA）是通过信息素的累积和更新而收敛于最优路径，具有分布、并行、全局收敛能力，但是其缺点是初期信息素匮乏，求解速度较慢。本文算法吸取了GA和AC的优点，首先形成改进的GAAC算法，具体步骤如下：

（1）进行遗传算法编码、选择、交叉、变异运算，形成蚁群算法的新的寻优区［Pmin，Pmax］和初始化参数，将初始化参数分配给相应的蚂蚁，并将多态蚁群算法中对侦查蚂蚁获得的侦查素的定义运用到遗传算法率先得到的初始元素的信息量中，生成额外的信息素分布：

式中：dij表示由遗传算法得到的元素j所对应的目标函数值，表示由遗传算法得到的所有元素所对应的目标函数最小值［12］。定义蚁群算法中元素的信息量初值为τC，因此集合Ici（1≤i≤M）（M为待识别参数量）中的元素j的信息素初值重新设置为［9］：

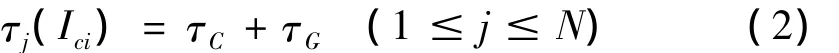
蚂蚁的数目为s，全部置于蚁巢，设置最大迭代次数NCmax。

（2）启动所有蚂蚁，每只蚂蚁从集合Ici开始，根据概率pj用轮盘赌法依次在每个集合中选择若干元素，直到蚁群全部到达食物源，蚂蚁的转移概率为：

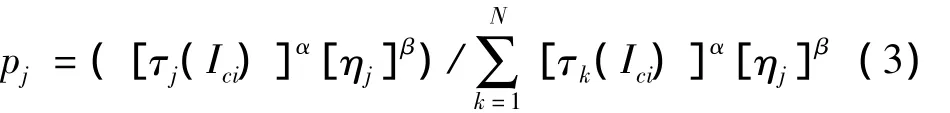
（3）当所有蚂蚁在每个集合中都选择了一定数量的元素后，计算用各蚂蚁所选元素做样本的输出误差，记录当前所选参数中的最优解，并保留。对所有集合Ici（1≤i≤2）中各元素的信息素按下式做调节

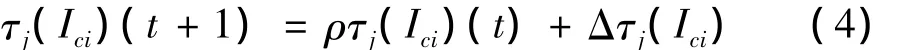
其中，参数0≤ρ≤1表示信息素的持久性，即残余信息素的保留部分。

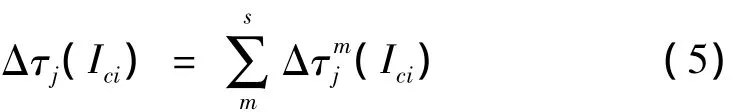
式中：Δτj（Ici）表示在本次循环中第k只蚂蚁在：

式中：Ici的第j个元素上留下的信息素，如式（6）所示，集合Q是常数，用来表示蚂蚁完成一次循环后所释放的信息素总量。它用于调节信息素的调整速度；Lm是以蚂蚁k选择的元素作为样本时的输出误差。

2 Ne-GAAC中的局部邻域搜索算法

在改进的GAAC算法中，每次循环结束时求出最优解，将其保留并与之前迭代后的最优解比较，当搜索到最优解可能出现的区域后，就需要一种搜索机制进行精细的局部搜索，准确的定位最优解的位置。本文设计出一种局部邻域搜索机制，用于Ne-GAAC中的局部搜索。

为了明确Ne-GAAC中的局部邻域搜索设计，首先需要定义几个相关的概念［10］：

局部邻域搜索启动临界值：预先设定的一个值，当GAAC搜索到的某一个解的适应值与目标值相等时，Ne-GAAC算法以GAAC搜索到的这个解为初始值启动一个局部邻域搜索。在D维空间中一点X（x1，x2，x3，…，xd），若存在一个正数，称任意一维上（xi-δ，xi+δ）为该维度上的邻域，则X所有维度上邻域构成的集合称为X基于维度的邻域，简称X的邻域，记为U（X，δ）。

禁忌邻域：记录在禁忌列表中的邻域称为禁忌邻域。对于禁忌邻域内的点，GAAC不进行搜索，任何进入禁忌邻域区的蚂蚁，自动重新分布。

基于以上的定义，可以设计Ne-GAAC中的局部邻域搜索算法：

（1）产生一个初始解，并将初始解置为当前解；

（2）产生当前解的基于维度的邻域，在该邻域内随机产生m个衍生解，评价这些解的适应值；

（3）若某个衍生解优于当前解，将该衍生解置为当前解，算法结束，否则转下一步；

（4）所有衍生解均劣于当前解时，转（2）；若重复操作若干次后仍未寻找到比当前解更优的解，表明该处极有可能是局部优化区，结束该局部邻域搜索区的搜索，算法结束。

3 Ne-GAAC的算法及流程图

3.1 Ne-GAAC的算法设计

（1）Ne-GAAC算法启动，经过遗传算法迭代形成蚁群算法初始参数及寻优区间，运行蚁群算法，设置最大迭代次数。

（2）判断是否达到最大迭代次数，若是，算法结束；否则，转下一步；

（3）GAAC迭代，在每次循环结束时求出最优解，将其保留并与之前迭代后的最优解比较，若多次寻优中出现了停滞和陷入局部最优问题，则满足局部邻域搜索启动条件，将这个解传递给LNeS作为初始解，把初始解置为当前解，设置m值和δ值，初始化一个局部邻域搜索，将初始解的邻域记入禁忌邻域，然后转下一步。

（4）根据当前解和当前m值、δ值，按照局部邻域搜索算法依次进行一次迭代。若搜索到比当前解更优的解，将该解置为当前解，转（2）；若既未搜索到满足误差条件的解，也未搜索到比当前解更优的解，则按给定条件重复搜索直到得到满足条件的解，结束该邻域搜索，然后转（2），否则，保持当前解不变，然后转（2）。

3.2 Ne-GAAC流程图

流程图如图1所示：

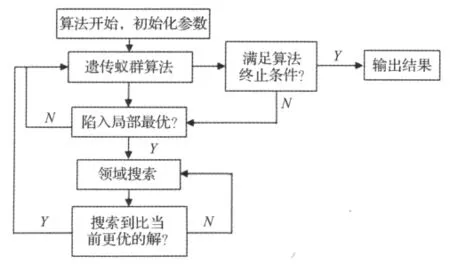
图1 Ne-GAAC算法流程图Fig.1 Flowchart of Ne-GAAC

4 仿真算例

4.1 经典函数验证

考虑 Duffing系统［13］：

利用本文方法识别系统进入混沌运动时参数a，b的取值见表1。

表1 a、b的识别结果Tab.1 Identification results of a，b

通过表1可以看出，利用本方法识别非线性系统中的参数可以取得较好的识别结果。

4.2 具有非线性刚度和碰摩的转子模型

具有非线性刚度和碰摩的转子系统模型如图2所示，对于具有非线性刚度的转子系统，其非线性刚度可以采用振动位移或速度的多项式函数形式表示，根据文献中实验结果，以线性项和立方项之和来表示源于中性轴伸长和对称的转轴材料物理非线性因素，其非线性应力—应变关系为［14］：

图2 单盘转子模型Fig.2 Model of rotor system

其对应的转轴弹性力可以表示为：

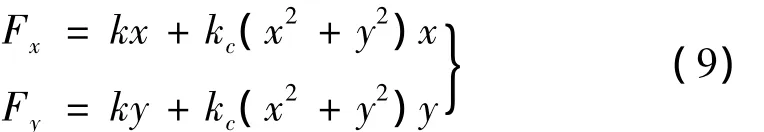
式中：k和kc分别为转轴材料的线性和非线性刚度项系数。

转子和定子间发生碰摩如图3所示，在x-y坐标系中碰摩力化为：

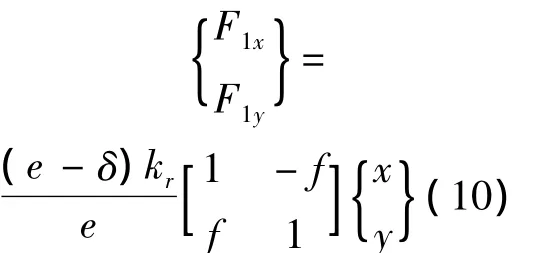
图3 碰摩力模型Fig.3 Model of rub-impact

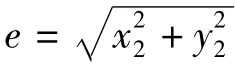
忽略两端支承的振动，不考虑转轴的质量，则具有非线性刚度和线性阻尼的碰摩转子系统动力学方程如下：

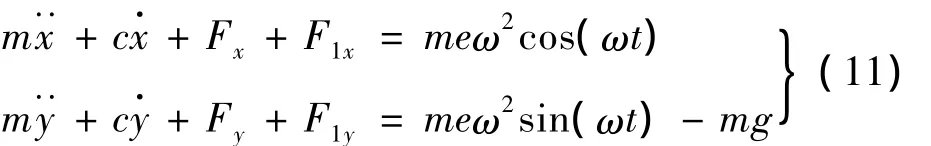
利用四阶龙格库塔法求解。

4.3 参数和目标函数选取

4.3.1 参数设置

表2给出了Ne-GAAC方法的参数选取，本文识别的参数为非线性碰摩转子的碰摩刚度kr，非线性刚度kc和摩擦系数f，参数范围分别为kr∈（1.0e5，1.0e7），kc∈（1.0e12，1.2e14），δ∈（1.0e-4，1.0e-6）。

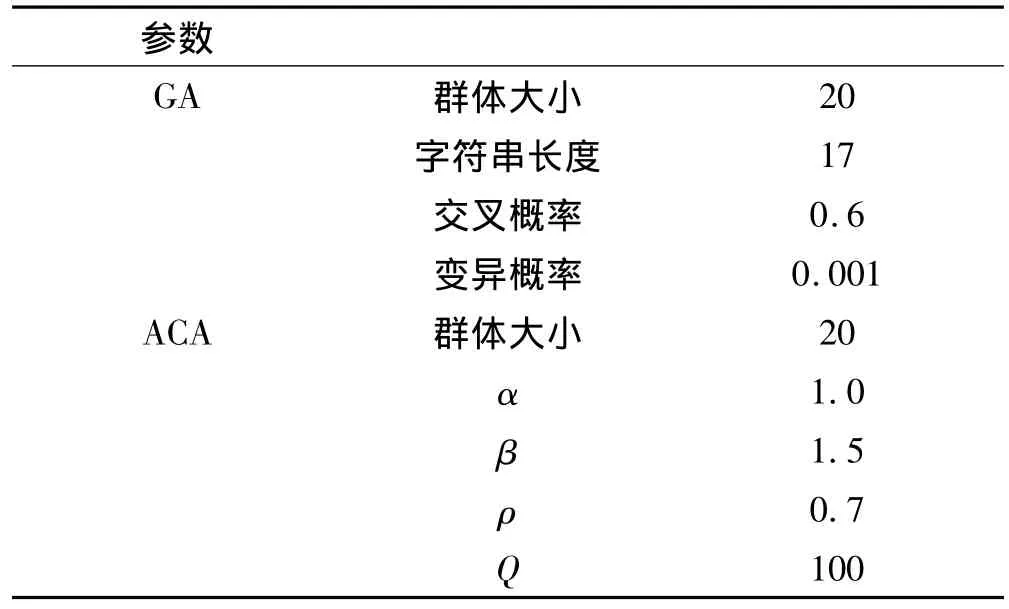
表2 Ne-GAAC方法的参数选取Tab.2 Control parameters of Ne-GAAC

4.3.2 目标函数选择

在工程优化问题中，目标函数的选择也是非常重要的，本文选用公式（12）-（14）三种不同形式的目标函数，通过对比得到最适宜求解非线性转子系统的目标函数。

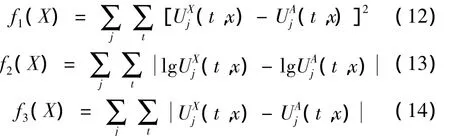
其中，U为响应值，X和A分别为仿真和分析结果，j为计算节点的位移向量，t为迭代时间。

4.4 结果分析

当ω=400，1 100，1 250 rad/s（单周期，双周期，混沌）情况下，三个参数的识别结果见表3。

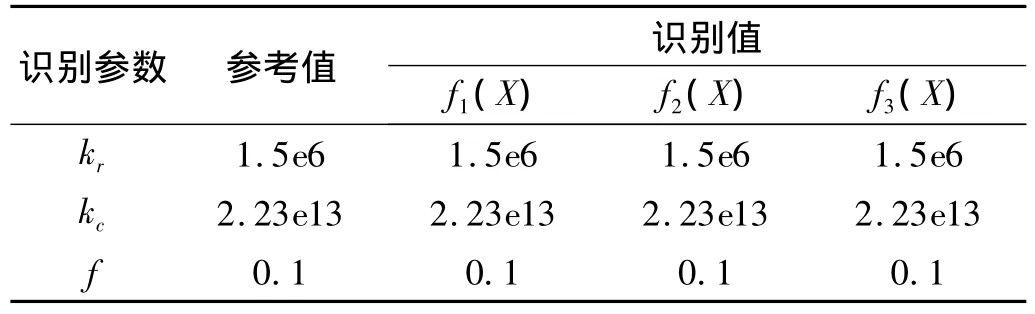
表 3 ω =400，1 100，1 250 rad/s（单周期、双周期、混沌）识别结果Tab.3 Identification results when ω =400，1 100，1 250 rad/s

表3为不存在噪声时单周期、双周期、混沌状态下的识别结果，对于三种形式的目标函数，识别值与参考值一致。

表4～表6为具有高斯白噪声（0，0.01）时，取20组随机样本的识别结果，由表格中的数据可以看出，转子系统由稳定向不稳定过渡的过程中，采用f1形式的目标函数识别结存在的误差较大，采用f2、f3两种形式的目标函数进行识别均能得到满意的识别结果。

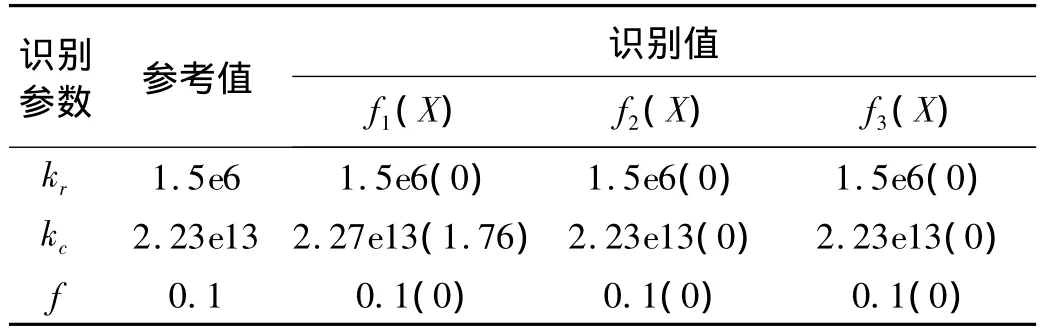
表4 ω=400 rad/s时（单周期）具有高斯噪声下的识别结果Tab.4 Identification results with Gaussian noise when ω=400 rad/s

表5 ω=1 100 rad/s时（双周期）具有高斯噪声下的识别结果Tab.5 Identification results with Gaussian noise when ω=1 100 rad/s

表6 ω=1 250 rad/s时（混沌）具有高斯噪声下的识别结果Tab.6 Identification results with Gaussian noise when ω=1 250 rad/s

当ω=1 250 rad/s并含有噪声（0，0.01）时，考虑目标函数为f2的形式时非线性刚度kc寻优区间的优化过程，如图4所示，由图4可以看出经过遗传算法优化后区间范围明显缩小，从而可以很好的提高蚁群算法的运算速度。图 5给出了非线性刚度kc的识别过程，其中1代表改进的GAAC算法，2代表邻域搜索算法，当GAAC达到给定的条件后进入局部邻域搜索，经过改进的GAAC和邻域搜索算法的循环迭代，最终得到了非线性刚度的识别结果。

表7通过Ne-GAAC、ACA、GA三种算法的对比可以看出，本文所提出的Ne-GAAC方法在非线性转子系统的参数识别中具有收敛速度快、运算效率高的优点。

表7 ω=400 rad/s不含有噪声时Ne-GAAC、ACA、GA算法数据比较Tab.7 Comparison of identification results for Ne-GAAC、ACA、GA without Gaussian noise when ω =400 rad/s

5 结论

本文从智能优化算法出发，考虑了遗传算法和蚁群算法的不同特点，形成了改进的GAAC算法，有效的弥补了两种算法的不足，同时为了能够更精确的定位最优解，将邻域搜索机制与改进的GAAC算法相结合，形成了Ne-GAAC算法，通过算例验证充分说明了本算法在不含有噪声的非线性转子系统参数识别中能够准确的识别非线性参数，当该系统存在噪声时，在不同非线性特性下也能得到较好的识别结果。三种目标函数的结果对比，也可以得到在非线性转子系统的参数识别中应采用f2形式的目标函数，能够获得最为满意的识别结果，最终通过三种算法的对比更加充分的是说明Ne-GAAC算法在非线性转子系统的参数识别方面具有收敛速度快、运算效率高的优点。

［1］Assis E G，Steffen J R V.Inverse problem techniques for the identification of rotor-bearing systems［J］.Inverse Problems in Engng，2003，11（1）：39–53.

［2］卢文秀，褚福磊，郭 丹.基于遗传算法的碰摩位置辨识［J］.清华大学学报（自然科学版），2005，45（2）：208-211.

［3］Kirkpatric S.Optimization by simulated annealing［M］.Science，1983，220（320）：671-680.

［4］周 明，孙树栋.遗传算法原理及应用［M］，国防工业出版社，1999：18-64.

［5］Dorigo M，Maniezzo V，Colorni A.Ant System：Optimization by a Colony of Cooperating Agents［J］.IEEE Transactions on Systems，Man，and Cybernetics-PartB：Cybernetics，1996，26（1）：29-41.

［6］Hagemana J A，Wehrens R，Van Sprang H A，et al.Hybrid genetic algorithm-tabu search approach for optimising multilayer optical coatings［J］.Analytica Chimica Acta，2003，490：211-222.

［7］Hsiao C T，Chahine G，Gumerov N.Application of a hybrid genetic algorithm/Powell algorithm and a boundary element method to electrical impedance topography［J］.Journal of Computational Physics，2001，173：433 454.

［8］ Renders J M，Flasse S P.Hybrid methods using genetic algorithms for global optimization［J］.IEEE Trans Syst Man Cybern Part B，1996，26（2）：243-258.

［9］杨剑峰.基于遗传算法和蚂蚁算法求解函数优化问题［J］.浙江大学学报（工学版），2007，41（3）：427-430.

［10］吴 亮，蒋玉明.融合粒子群和局部邻域搜索的优化算法［J］.计算机工程与设计，2010，31（7）：1557-1557.

［11］ Kim Y H，Yang B S，Tan A C C.Bearing parameter identification of rotor-bearing system using clustering-based hybrid evolutionary algorithm［J］.Struct Multidisc Optim，2007，33：493-506.

［12］段海滨.蚁群算法原理及其应用［M］.北京：科学出版社，2005：136-139.

［13］刘秉正.非线性动力学与混沌基础［M］.长春：东北师范大学出版社，1995：139-148.

［14］罗跃纲.转子系统故障的若干非线性动力学问题及智能诊断研究［D］.沈阳：东北大学，2002.