异步电机定子的振动与模态分析

韩 伟，贾启芬，邱家俊

（天津大学 机械学院，天津 300072）

异步电机在很多工业领域具有广泛的应用历史，然而至今仍有很多问题有待解决。其中的一个问题就是电机运行过程产生的电磁噪声，这是由高频电磁力引起电机强迫振动产生的，当电机结构发生共振时，电机的噪声会更大［1-2］。为了降低噪音，预测电机产生的振动和噪声需要准确地确定谐振频率和激振力，因此必须对电机定子结构的固有频率和振动特性进行详细的研究。国内外不少学者进行了这方面的研究。文献［3-4］对电机定子的振动特性进行了试验研究；文献［5］利用解析法计算了异步电机定子的固有频率；文献［6］研究了电机定子齿槽对异步电机振动噪声的影响。随着有限元方法的引入和发展，不少研究者开始利用有限元法和试验相结合的方法对电机的振动特性进行了研究，文献［7］利用有限元和实验相结合的方法研究了绕组对异步电机定子的固有频率的影响，文献［8-10］利用有限元法和实验相结合的方法对异步电机的固有频率和振型进行了详细的研究；文献［11］提出了一种非破坏性测定电机定子叠片了大型异步电机的振动模态；文献［12］利用有限元方法研究也存在着一些问题，概括起来问题主要集中在以下几个方面：①由于铁芯是由长度为2～6 mm的空心圆柱硅钢片冲制叠压而成，各片之间还通过绝缘材料隔开，故铁芯不是简单的连续弹性介质，不能把电机铁芯叠片结构简化为硅钢实体或者弹性模量较小的各向同性体；② 计算结果分析仅局限于定子的径向平面振动模态，对于有效防止电机产生其它三维振动模态的共振参考价值不大。因此，有必要进一步改进电机的有限元建模方法，提高计算结果的准确度，同时系统的分析定子的三维振动模态。

本文基于异步电机简化的三维物理模型，建立了各种不同的电机定子的有限元模型，通过比较不同的定子有限元模型的计算结果准确度，改进了定子的有限元建模方法，系统的分析了定子三维振动模态。试验样机的有限元计算结果与实验结果进行了比较验证。

1 数学模型和研究方法

振动模态分析，就是利用系统固有频率的正交性，以系统的各阶模态向量所组成的模态矩阵作为变换矩阵，对选取的物理坐标进行线性变换，使得振动系统以物理坐标和物理参数所描述的、互相耦合的运动方程组能够变为一组独立的模态方程。由于坐标变换是线性变换，因而系统在原有物理坐标系中，对于任意激励的响应，便可视为系统各阶模态的线性组合，故模态分析方法又称为模态叠加法。而各阶模态在叠加中所占的比重或加权系数则取决于各阶模态的响应。取一单元体，设单元体的动能为T，应变能为U，阻尼消耗的能量为Wd，外力的势能为We。建立拉格朗日函数为：

利用哈密顿原理和应力-应变关系、应变-位移关系可以导出单元的运动方程为：

其中（·）表示对时间的求导，下标和上标e表示单元，Me表示单元体的质量矩阵，Ce表示单元体的阻尼矩阵，Ke表示单元体的刚度矩阵，Fe表示单元体的载荷矩阵，qe表示单元体的节点位移。对整个系统的各单元集合，便可以得到振动系统的运动方程为：

式中：M为系统整体的质量矩阵，C为系统整体的阻尼矩阵，K为系统整体的刚度矩阵，F为节点力矢量。而固有频率一般为无阻尼自由振动，令F={0}和C={0}，根据微分方程理论，式（3）的解可以表示为：

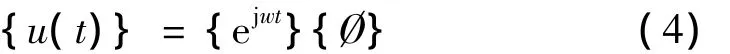
根据线性方程理论有非零解的充分必要条件为：

解出满足式（5）、（6）的频率w和对应的非零解向量Ør（r=1，2，3，…，n），其中w和Ør分别为电机的固有频率和固有振型。

作为结构力学的经典内容，自由振动模态分析的理论和计算方法都比较成熟，并形成了各种数值分析软件。本文利用有限元软件Ansys对异步电机进行三维有限元分析，在一定的简化基础上，将电机模型全部拉伸为8面体单元，保证了计算结果的精确度，提高了工作的效率。同时结合实验数据，全面研究异步电机定子的模态和固有频率。

2 三维有限元建模

为便于比较，以一台4 kW、三相异步电机实验样机为例，构建了6种基本的有限元计算模型。机壳的材料为铸铁，定子铁芯叠片的材料为硅钢片，硅钢片表面涂有一层薄绝缘材料，绕组的材料为铜。

图1 两种铁芯模型Fig.1 Two modal of the core

模型Ⅰ 只考虑了定子铁芯、绕组和机壳（没有散热筋和底脚）在通常的电机结构中，绕组通过绝缘树脂与定子铁心相粘连，其对定子铁心的刚度影响较小，其影响主要以附加质量体现［13］，将绕组的质量折算到定子齿中，使定子齿的密度增大，以考虑绕组对定子振动系统的影响。由于铁芯是由很多薄硅钢片叠压而成的离散介质体，如果要建立铁芯的实际模型，则其建模与计算的难度将是无法估计的，本文采用等效替换的方法，把铁芯叠片简化为8个相同的离散单元体，每个单元体与机壳均采用刚性联结，且8个单元体之间无轴向相对位移。铁芯的建模过程如下：首先只建立铁芯实体模型的1/8，然后通过移动复制1/8铁芯实体建立8个相同的铁芯段，8个铁芯段再分别与机壳进行体粘结布尔操作，对每个铁芯段分别进行网格划分，然后利用耦合命令CPINTF耦合单元体之间重合节点的轴向位移。铁芯的虚拟模型和有限元模型如图1所示，绿色部分表示耦合此处重合节点的轴向位移。该定子模型如图2（a）所示，定子各部分的材料属性如表1所示。

表1 电机各部分的材料特性Tab.1 Material properties of motor

模型Ⅱ在模型Ⅰ的基础上添加了轴向散热筋和加强筋，主要是考查散热筋和加强筋对定子固有频率的影响。其各种材料属性同表1。有限元模型如图2（b）。

模型Ⅲ在模型Ⅰ的基础上添加了底脚，主要是考查底脚对定子固有频率的影响。其各种材料属性同表1。有限元模型如图2（c）。

模型Ⅳ在模型Ⅰ的基础上既添加了轴向散热筋和加强筋，又添加了底脚。同时考查轴向散热筋、加强筋察和底脚对定子固有频率的影响。其各种材料属性同表1。有限元模型如图2（d）。

图2 模型Ⅰ到模型Ⅳ的有限元计算模型Fig.2 FE Models of modeⅠ to Mode Ⅳ

模型Ⅴ在模型Ⅳ的基础上，铁芯简化为材料均匀各向同性的连续体，其弹性模量取为 1.521 ×1011N/m2［10］。其它的材料属性同表1。

模型Ⅵ 在模型Ⅳ的基础上，铁芯简化为硅钢实体，其弹性模量取为2.058 ×1011N/m2［2］。其它的材料属性同表1。

3 结果分析

对上述模型做无任何机械约束的自由振动模态分析，得到定子三维振动的前五阶固有频率如表2所示。模型Ⅳ的前五阶固有振型如图3所示。比较模型Ⅰ的计算结果与实验结果，发现模型Ⅰ的前五阶固有频率均与实测值误差较大，其中，第一阶的固有频率的计算结果与实测值的误差最大，为38.89%，说明模型Ⅰ的计算结果的准确度很低。比较模型Ⅱ的计算结果与实验结果，发现模型Ⅱ的前五阶固有频率与实测值最大的最大误差为15.58%，说明模型Ⅱ的计算结果与模型Ⅰ的计算结果相比，模型Ⅱ的计算结果的准确度有了很大的提高。同理，模型Ⅲ的计算结果与模型Ⅱ的计算结果相比，模型Ⅲ的计算结果的准确度更高。而模型Ⅳ的计算结果与实验结果相比，最大误差不超过9%，模型Ⅳ的计算结果的准确度是上述模型中最高的。模型Ⅴ的计算结果与实验结果相比，计算所得的固有频率值最大误差为43.39%，说明模型Ⅴ的计算结果的准确度比模型Ⅰ还低。模型Ⅵ的计算结果与实验结果相比，计算所得的固有频率值最大误差为53.67%，说明模型Ⅵ的计算结果的准确度是上述模型中最低的。

表2 模型Ⅰ－Ⅵ的结果与实测值的比较Tab.2 Comparison of modalⅠto Ⅵanalysis results with measured Results

图3 模型Ⅳ的前五阶振动模态Fig.3 The first to fifth mode shapes of modalⅣ

另外，由图3和表2可知，模型Ⅳ得到了多个低阶固有频率和振型的计算结果，在前五阶模态中，有2个椭圆振动模态、3个低阶轴向和径向平面振动的组合模态。其中一、四、五阶模态为轴向和径向平面振动的组合模态，二、三阶为椭圆振动模态。与文献［2，13］的计算结果相比，很多没有被计算和分析的低阶模态，都被准确地计算出来了，这些低价振动模态都有可能被不平衡电磁力激起，准确地计算和分析这些模态对于降低电机的振动与噪声具有重要的参考价值。

综合以上分析，可以得到如下一些结论：

（1）在电机定子的有限元建模过程中，充分考虑散热筋、加强筋和底脚对定子固有频率的影响，可以有效提高定子固有频率的计算结果的准确度。

（2）在电机定子的有限元建模过程中，当把定子铁芯简化硅钢实体或者弹性模量取为1.521×1011N/m2的均匀各向同性体时，定子模型的固有频率的计算结果与实验结果相比误差较大，尤其是轴向阶数m≠0的第一阶固有频率。由此可知，在计算定子的三维振动模态时，定子铁芯是不能利用硅钢实体或者其它的各向同性体［10］来等效替换的。

（3）根据本文的等效替换方法，把定子铁芯等效为多个离散的单元体（单元体的个数可通过多次试算得到）时，定子模型固有频率计算结果的准确度可以得到有效的提高。

（4）在综合考虑了散热筋、加强筋、底脚和铁芯结构对模型计算结果的影响之后，使得该有限元模型的计算结果达到了很高的准确度。

4 计算实例

为了进一步验证本文模态分析计算的有效性，根据实验样机数据，建立了一个考虑绕组、散热筋、加强筋、底脚、铁芯和端盖的有限元模型。绕组、散热筋、加强筋、底脚、铁芯等的建模处理方法均按照本文上节讨论所得的建模处理方法进行建模（模型Ⅳ的建模方法），端盖装配与机壳，两者之间可以视为紧密配合（贴合面无相对位移）。由于在实际的工作环境中，电机底脚通过螺纹与地面保持接触，螺纹的松紧对电机的振动具有重要的影响，情况比较复杂，故本文主要是对样机模型做三维的自由振动模态分析。试验样机的有限元模型如图4所示，表3列出了该模型的前三阶固有频率，图5为该模型的前三阶固有振型。

图4 实验样机的有限元模型Fig.4 FE modal of prototype motor

图5 模型Ⅶ的前三阶固有振型Fig.5 The first to fifth mode shapes of modalⅦ

5 实验

为了能够保证有限元模型计算结果的可靠性，对样机进行了实验模态分析。实验由两种工况组成，即：自由状态下不带端盖的定子实验模态分析、自由状态下带端盖的定子实验模态分析。根据实验要求，对自由状态下不带端盖的定子和自由状态下带端盖的定子布置了40个测点，每个测点要测试两个方向的加速度响应信号（R和θ方向）。

表3 模态分析结果与实测结果对比Tab.3 Comparison of modal analysis to results with measured results

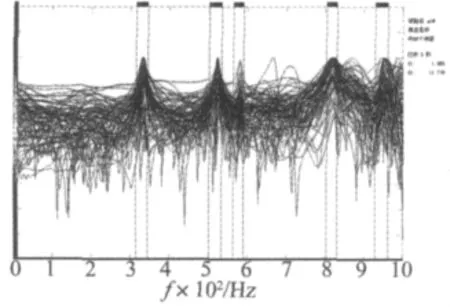
图6 自由状态下不带端盖电机定子的频响函数集中结果Fig.6 Frequency response functions results of unrestrained stator without end-shields

图7 自由状态下带端盖的电机定子的频响函数集中结果Fig.7 Frequency response functions results of unrestrained stator with end-shields

利用CL-YD-302系列力锤及力传感器单点激励第4点R方向，采用CA-YD-108压电式加速度传感器拾取各点R、θ方向的加速度信号。实验的分析带宽为1 000 Hz，共记录了40个力信号的时间历程，80个加速度响应的时间历程，将实验中采集到的每次激励的力信号、各测点两个方向响应的加速度信号数据，在模态分析软件上进行了以快速傅里叶变换为核心的数据处理工作，共获得了80个频响函数。图6和图7为所有的频响函数的集中结果显示。

在以上工作的基础上应用专用模态分析软件，进行实验对象的模态参数识别，得到了两种工况下电机定子的固有频率，表2为模型Ⅰ-Ⅵ的计算结果与无端盖定子实测值的比较，表3为实验样机的计算结果与实测值的比较。由表3可知实验频率和模态频率很接近，相对误差均低于10%，表明模态仿真是可靠的。

6 结论

本文利用三维有限元模态分析法，通过比较采用不同的有限元建模方法时不同定子模型固有频率计算结果的准确度，得出对离散的铁芯叠片结构，采用多个离散单元体等效替换的方法，与传统的简化方法相比，可以大大提高三维振动固有频率计算结果的准确度。采用本文的建模方法，综合考虑散热筋、加强筋、底脚和离散铁芯叠片结构对固有频率计算结果准确度的影响后，使得该有限元模型的模态计算结果达到了很高的准确度，能够满足工程精度要求，证实了本文的建模方法的优越性和模态分析计算的有效性。对于降低电机的振动与噪声具有重要的参考价值。

［1］ Ishibashi F，Noda S，Mochizuki M.Numerical simulation of electromagnetic vibration of small induction motor［J］.Proc-Electr Power Appl，1998，145（6）：528-534.

［2］吴建华.基于物理模型开关磁阻电机定子模态和固有频率的研究［J］.中国电机工程报，2004，24（8）：109-114.

［3］Girgis R S，Sc M，Ph D，et al.Method for accurate determination of resonant frequencies and vibration behavior of stators of electrical machines［J］.Proc，1981，182（1）：1-11.

［4］ Verma P S P，Eng B S，Ing D，et al.Experimental verification of resonant frequencies and vibration behaviour of stators of electrical machines， part 2-experimental investigations and results［J］.Proc.，1981，128（l）：22-32.

［5］ Ishibashi F，Kamimoto K， Hayashi T，et al. Natural frequency of stator core of small induction motor［J］.Proc-Electr power Appl，2003，150（2）：210-214.

［6］ Kobayashi T，Tajima F，Ito M，et al.Effects of slot combination on acoustic noise from induction motors［J］.Transactions on Magnetics，1997，33（2）：2101-2104.

［7］Noda S，Mori S，Ishibashi F，et al.Effect of coils on natural frequencies of stator cores in small induction motors［J］.Transactions on Energy Conversion，1987，2（1）：93-99.

［8］ Watanabe S，Kenjo S，Ide K，et al.Natural frequencies and vibration behaviour of motor stators［J］.Transactions on Power Apparatus and Systems，1983，102（4）：949-956.

［9］ Ishibashi F，Kamimoto K，Noda S，et al.Small induction motor noise calculation［J］. Transactionson Energy Conversion，2003，18（3）：357-361.

［10］ Ishibashi F，Matsushita M，Noda S，et al.Change of mechanical natural frequencies of induction motor［J］.Transactions on Industry Applications，2010，46（3）：922-927.

［11］ Tang Z J，Pillay P，Omekanda A M，et al.Young＇s modulus for laminated machine structures with particular reference to switched reluctance motor vibrations［J］.Transactions on Industry Applications，2004，40（3）：748-753.

［12］王天煇，王凤翔.大型异步电机定子振动与模态分析［J］.中国电机工程报，2007，27（12）：41-45.

［13］孙剑波，詹琼华，黄 进.开关磁阻电机的定子振动模态分析［J］.中国电机工程报，2005，25（22）：148-152.