一种新的估计瞬时频率的方法-经验包络法

郑近德，程军圣，杨 宇

（湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082）

频率在信号处理、通信、物理学等领域都是一个很重要的概念，它是刻画波形的周期性质和振荡模式的一种属性。频率在物理上定义为周期的倒数，据此定义，如果要定义频率，必须有一个完整的波形才能有周期。然而对一些平稳或非平稳信号而言，不存在固定的周期，但它却有一定的振荡模式，其频率随时间不断变化，传统的频率的定义所具有的物理意义无法明确地描述其频率瞬变现象。因此，需要一个类似于频率的物理量来反映和刻画信号这一性质。于是相关学者提出了瞬时频率的概念。Carson等提出了瞬时频率的概念，并对其定义进行了详细研究。Gabor［1］给出了解析信号的概念，Ville等［2］提出了现在普遍接受的一般实信号的瞬时频率（instantaneous frequency，简称IF）的定义。即，实信号的瞬时频率定义为该信号所对应的解析信号的相位函数关于时间的导数。其中，解析信号是基于希尔伯特变换而定义的。

常用的求信号的瞬时频率的方法有：相位差分法［3］，锁相环法［4-5］，基于希尔伯特变换的解析信号法［6］，Teager能量算子法［7-8］，以及 LMD 方法中的反余弦法［9-10］。这些方法即有自己的优势，但有各自的缺点。相位差分法包括前向差分，后向差分和中心差分，效果比较好的是中心差分法，其优点在于对线性调频信号是无偏的，且具有零延迟；而且它对应为一系列时频分布的一阶矩。但其缺点是对噪声太敏感，对含噪信号表现很大的方差［3］。Teager能量算子法是数学表达式的近似变换，原理简单，并且无需进行复数计算，计算量减小，因此近年来在求取信号的瞬时特征方面得到广泛应用，取得了很好的效果［8］。由于Teager能量算子法基于假设信号具有线性相位（即瞬时频率为常数）且假设瞬时幅值近似为常数，因此，对于大部分窄带信号有很好的效果，但如果瞬时幅值是时间的瞬变函数，或者波形有波内调制（intrawave modulations）或谐波失真（harmonics distortion），能量算子法将会有很大的误差，甚至不能使用。

对于单分量实信号，瞬时频率最一般的求法是，通过希尔伯特变换定义其解析信号，瞬时频率定义为其解析信号相位的导数。这是学术界普遍接受的定义瞬时频率的方法。但是科恩指出，这种定义有几种自相矛盾的佯谬结论［11］。首先，瞬时频率可以不是频谱中的频率之一。其次，如果有只有少数的明显的频率组成的一个线性频谱，那么瞬时频率可以是连续的，而且可以在无数个值范围内变化。第三，虽然解析信号的频谱对于负频率为零，但瞬时频率却可以是负的。第四，对于一个带限信号，它的瞬时频率可以在频带之外。第五，为了计算某一时刻的解析信号，却要必须知道全部时间的信号。事实上，不是所有的单分量信号都可以进行希尔伯特变换，必须要满足Bedrosian定理和 Nuttal定理［12］。

以上的讨论一般只适合单分量信号，如果是多分量信号，一般是先通过 EMD［6］，LMD［9-10］等方法将其分解为若个单分量信号和一个残余项之和。再对得到的单分量信号求瞬时频率，进而求得多分量信号的瞬时频率。

基于希尔伯特变换的以上条件限制和问题，本文尝试避开希尔伯特变换求瞬时频率，提出了一种新的估计瞬时频率的新方法-经验包络法（empirical envelope method，简称 EE）。

1 经验包络法

经验包络法的核心是经验调幅调频分解（简称经验AMFM分解），因此，下文先介绍经验AMFM分解。

1.1 经验AMFM分解［12］

一般单分量信号x（t）未必是形如x（t）=a（t）cosφ（t）的形式，而把x（t）写作调幅部分和调频部分的乘积的形式对于求瞬时频率是非常重要的，能量算子法和反余弦法都基于此假设。因此有必要研究把任意的单分量信号唯一地写作调幅和调频部分的乘积形式的一般方法。诺顿·黄等［12］提出了一种把一般单分量信号特别是内禀模态函数写成调幅调频形式的方法，称之为经验调幅调频分解。具体步骤如下：

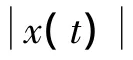
（2）三次样条拟合极值点（τk，xk）（k=1，2，…，M），得到信号的经验包络函数a11（t）。对于一般实信号极值点是固定的，因此经验包络函数也是唯一定义的。得到经验包络函数后，可以用它来标准化数据，x（t）除以经验包络函数a11（t），得：

（3）x1（t）是标准化的数据，理论上x1（t）的包络估计函数a12（t），应该小于等于1，否则，对x1（t）重复上述步骤经过n次迭代：

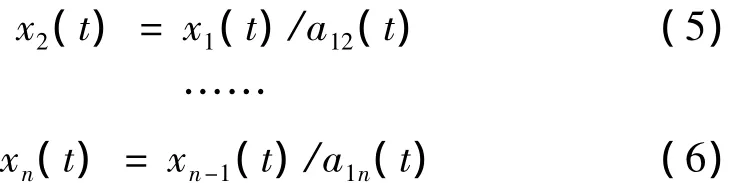
直到a1n（t）≤1，即x1n（t）为一纯调频函数，迭代结束。记纯调频信号x1n（t）为F（t），则存在φ（t），使得：

（4）x（t）的调幅部分定义为：

至此，x（t）被分解为a（t）cosφ（t）的形式。

上述过程经验地实现了信号的调幅调频分解。一般地，上述过程收敛过程比较快，迭代次数不会太多，1～3次即可实现数据的标准化。如经验模态分解一样，上述方法只是经验分解，没有解析的表达式和严格的数学证明。另外，分解过程可能会引起原始信号波形的失真，但失真的总和是可以忽略不记的，因为上述过程有过零点周期性地严格控制着，而过零点的位置是不变的。

本文在经验AMFM分解的基础上提出了一种新的估算瞬时频率的方法-经验包络法。

1.2 经验包络法

由经验AMFM分解过程易知，任意单分量信号x（t）可以近似写作x（t）=a（t）cosφ（t）的形式，F（t）=cosφ（t）的瞬时频率即为原始信号的瞬时频率，因此，只要求出F（t）的瞬时频率即可。由此提出了如下的求瞬时频率的经验包络法：

（1）首先由经验AMFM分解，任意单分量信号x（t）可写作：x（t）=a（t）cosφ（t）。

（2）再令F（t）=cosφ（t），并对其两边求导，得：

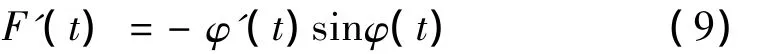
式中，由于φ'（t）=2πf（t）一般为线性或相对载波部分sinφ（t）变换缓慢的函数，因此可视φ'（t）=2πf（t）为F'（t）的包络部分。

（3）再对F'（t）进行经验AMFM分解，得：

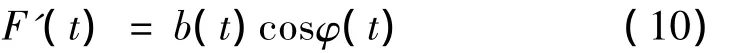
这里的b（t）近似为上式中的φ'（t）。因此，原信号的瞬时频率为：

经验包络法是基于信号的经验AMFM分解提出的，计算简单方便，不需要繁杂的程序和极值点处的特殊处理，只要应用两次经验AMFM分解和一次求导即可。经验包络法的核心是经验AMFM分解，分解的效果直接决定了求得的瞬时频率的准确性。这里有个矛盾，为了得到的纯调频信号，则需要增加迭代的次数，但由于采用三次样条拟合包络，迭代的次数增加，拟合的误差会增大，求得的瞬时频率误差也会随之增大。如果迭代的次数过少，三次样条拟合的误差减小，得到的纯调频信号的个别点仍大于1。实验表明，经验包络法对信号的纯调频程度要求不高，即允许有个别点的值大于1，对结果影响很小。因此，一般迭代次数越少，经验包络法求得的瞬时频率效果会更好。而如果得到的调频信号有大于1的点，反余弦法则会出现突变，甚至不能使用，这也是经验包络法优于反余弦法之处。经验包络法求取瞬时频率的流程如图1所示。

图1 经验包络法流程图Fig.1 Flow-process diagram of emprical envelope method

事实上，经过经验AMFM分解，信号被分解为调幅部分和纯调频部分的乘积，对于纯调频信号F（t）=cosφ（t），可以采取类似于LMD方法中的反余弦法求取瞬时频率，即对F（t）=cosφ（t）两边求反余弦，得：

φ（t）相位以2π展开，再对其求导得到瞬时频率：

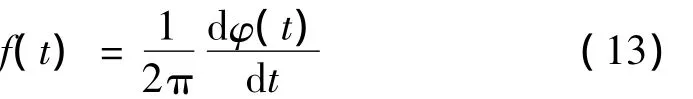
基于反余弦法求瞬时频率，直接方便，不需要希尔伯特变换，而且由于是基于信号本身的反余弦计算，计算量较小，精确性较高。但反余弦法的缺点是其求得的瞬时频率在信号的极值点处会有不稳定的突变，需要平滑处理。并且对信号的标准化要求较高，如果标准化后的数据有大于1的点，则在该处反余弦法会有很大的误差。

文献［12］提出另一种基于经验AMFM分解的估计瞬时频率的方法，即标准希尔伯特变换法（Normalized Hilbert transform，简称NHT）。内禀模态函数经过经验AMFM分解，得到纯调频信号F（t）=cosφ（t），此时F（t）瞬时幅值为1，不再受Bodrosian定理的限制，因而可以对其希尔伯特变换，求取瞬时频率。由于信号满足Bodrosian定理，克服了希尔伯特变换会出现负频率的缺陷，比直接希尔伯特变换有了很大的提高。但由于仍然采用希尔伯特变换，在端点处会产生能量泄露，因此端点效应仍无法避免。

2 仿真信号分析

为了比较希尔伯特变换，标准希尔伯特变换，反余弦法和经验包络法四种方法求取瞬时频率的效果和优缺点，先考察信号：

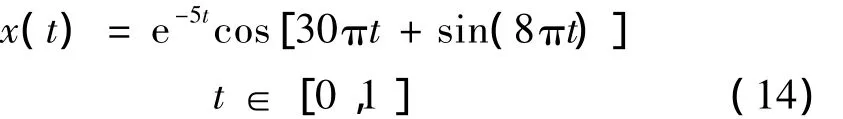
由于信号简单和篇幅关系，信号时域波形略。分别用上述四种方法求式（14）所示信号的瞬时频率，结果如图2所示。其中，HT表示希尔伯特变换法，NHT表示标准希尔伯特变换法，ACOS表示反余弦法，EE表示经验包络法，Truth表示信号的真实频率，无特殊说明，下同。

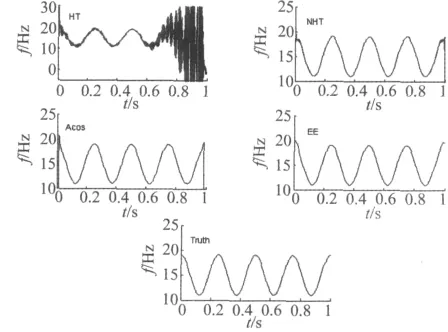
图2 不同方法求得的x（t）的瞬时频率与其真实频率Fig.2 IFs get by different methods of x（t）and its true IF

为了说明各种方法求得瞬时频率的效果和精确性，误差分析采用相对误差来作为评价指标。相对误差定义为：

其中，A是真实值，这里为信号的真实频率。Δ是绝对误差，这里为各种方法求得的瞬时频率与真实频率差值的绝对值。

上述四种方法计算式（14）信号的瞬时频率的相对误差如表1。

表1 瞬时频率的相对误差Tab.1 The relative error of IFs

由图2和表1知，希尔伯特变换求取的瞬时频率有明显的端点效应，而且还出现了负频率，相对误差较大；经过标准化后求取的瞬时频率负频率消失，相比希尔伯特变换有了很大的提高，但仍然有端点效应；反余弦法求得的瞬时频率与理论瞬时频率吻合，但在两端部分有突变现象；而由本文提出的经验包络法求得的瞬时频率和真实瞬时频率最为接近，而且相对误差比其他方法较小，此例初步说明了经验包络法的有效性和优越性。

上述考察的是单分量信号，初步表明了本文方法有很好的效果，进一步考察多分量信号：

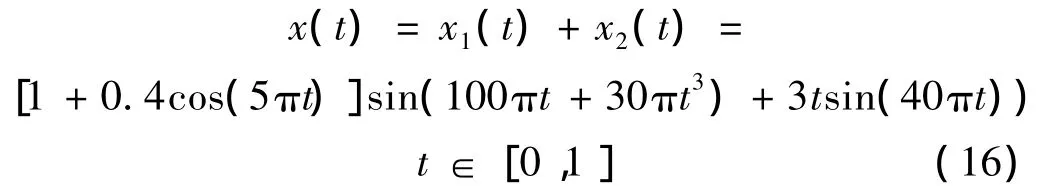
信号x（t）是调幅调频信号x1（t）和调幅正弦信号x2（t）的叠加。其时域波形及其EMD分解结果如图3所示。

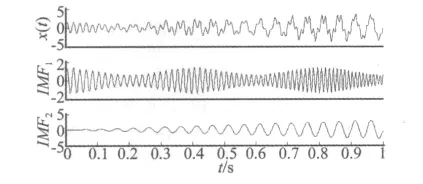
图3 x（t）及其EMD分解结果Fig.3 x（t）and its EMD decomposition results

分别用上述四种方法求取分量IMF1，IMF2的瞬时频率，结果如图4、图5所示。需要说明的是，由于分量IMF1和IMF2理论上分别对应为调幅调频信号x1（t）和调幅正弦信号x2（t），故图4和图5中的真实频率Truth分别表示x1（t）和x2（t）的瞬时频率。

上述四种方法求得的第一个分量IMF1的瞬时频率的相对误差如表2所示。

图4 不同方法求得的IMF1的瞬时频率Fig.4 IFs of the IMF1calculated by different methods

表2 不同方法求得IMF1的瞬时频率的相对误差Tab.2 Relative errors of the IFs of IMF1 calculated by different methods

由图5和表2知，希尔伯特变换和标准希尔伯特变换法求得的IMF2瞬时频率端点效应较严重。而反余弦法和经验包络法求得的瞬时频率结果都非常接近理论瞬时频率，二者都有非常好的效果。但经验包络法求得的瞬时频率的相对误差比反余弦法更小。

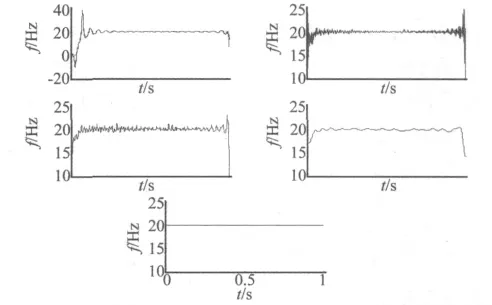
图5 不同方法求得的IMF2的瞬时频率Fig.5 IFs of the IMF2calculated by different methods

上述四种方法求得的第二个分量IMF2的瞬时频率的相对误差如表3所示。

表3 不同方法求得IMF2的瞬时频率的相对误差Tab.3 Relative errors of the IFs of IMF2 calculated by different methods

由图5和表3可知，由希尔伯特变换求得的IMF2的瞬时频率出现了负频率，而标准希尔伯特变换克服了这一缺点，有了很大的提高，但端点效应很明显。反余弦法求得的瞬时频率都有轻微的波动。而由经验包络法求得的瞬时频率相对误差最小，最接近理论值，与上述方法相比，经验包络法有明显的优越性。

需要说明的是，上述图4，图5中求得的IMF1，IMF2的瞬时频率的误差和以及端点效应，不仅仅是因为经验AMFM分解，还有一部分是因为EMD分解，因为EMD分解也会出现端点效应。

为更好地说明上述四种方法的分解效力，下面以实测信号为例来说明。图6是一外圈有凹槽的6311型球滚动轴承的振动加速度信号及其EMD分解的前四个IMF分量的时域波形。采样频率为4 096 Hz，采样点数为1 024，转频为25 Hz。

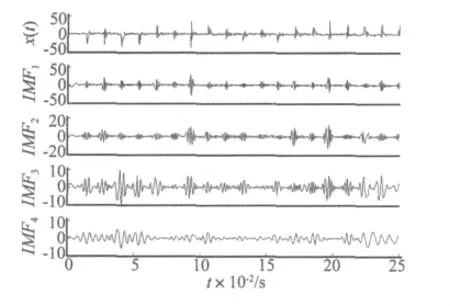
图6 轴承振动加速度信号时域波形及其EMD分解的前四个IMF分量波形Fig.6 Bearing vibration acceleration signal waveform and its first four components generated by EMD

由于前两个分量的瞬时频率较高，波动较大，不方便比较，因此，分别用希尔伯特变换，标准希尔伯特变换，反余弦法和经验包络法求第三个分量IMF3和第四个分量IMF4的瞬时频率，如下图7，8所示。

从图7和图8中可以看出，希尔伯特变换求得的瞬时频率有负频率，而且有端点效应，而反余弦法和经验包络法求得的瞬时频率较为理想。但从图8可以看出，反余弦求得的瞬时频率有突变点，经验包络法要优于反余弦法。

3 结论

提出了一种新的估计瞬时频率方法，经验包络法，并将其与希尔伯特变换，标准希尔伯特变换和反余弦法进行了比较，并通过仿真信号和实测信号分析，结果表明经验包络法具有一定的优越性。经验包络法的关键在于求取信号包络，经验调幅调频分解中是采用三次样条拟合信号绝对值的极大值而得，因此会有一定的拟合误差。如果提高求取包络的方法，经验包络法的准确性也将会有很大的提高。实例已表明有经验包络法有很好效果，但对此方法的使用范围，误差产生的较小等问题还需要进一步研究，以使其更完善和精确，应用更广泛。

［1］ Gabor D.Theory of communication［J］.Journal of the IEEE，1946，93：429-457.

［2］Ville J.Theorie et application de la notion de signal analyticque［J］.Cables et Transmissions，1948，2A（1）：61-74.

［3］张贤达.非平稳信号分析与处理［M］.北京：国防工业出版社，1998.

［4］Boashash B.Estimating and interpreting the instantaneous frequency of a signal-part 1：fundamentals［J］.Proceedings of the IEEE，1992，80（4）：520-538.

［5］Boashash B.Estimating and interpreting the instantaneous frequency of a signal-part 2：algorithms and applications［J］.Proceedings of The IEEE，1992，80（4）：540-568.

［6］Huang N E，Wu Z H，A review on Hilbert-Huang transform：method and its applications to geophysical studies［J］.Reviews of Geophysics，2008，46（2）：1-23.

［7］MaragesP， KaiserJF. Energy separation in signal modulation to speech analysis［J］.IEEE Transactions on Signal Process，1993，41（10）：3024-3051.

［8］ Kaiser J F.Some useful properties of Teager＇s energy operators［J］.Proc.IEEE Int.Conf.Acoust.Speech Signal Processing，1993（3）：140-158.

［9］Smith J S.The localmean decomposition and its app lication to EEG perception data［J］.Journal of the Royal Society Interface，2005，2（5）：443-454.

［10］程军圣，张 亢，杨 宇，等.局部均值分解与经验模态分解的对比研究［J］.振动与冲击，2009，28（5）：13-16.

［11］科恩著，白居宪，译.时频分析：理论与应用［M］.西安：西安交通大学出版社，1998.

［12］ Huang N E，Wu Z，Long S R，et al.On the frequency［J］.Advances in Adaptive Data Analysis.2009，1（2）：177-229.