高阶振型对高墩桥梁抗震性能的影响及其识别

卢 皓，管仲国，李建中

（同济大学 桥梁工程系，上海 200092）

跨越山谷的高墩桥梁在我国的铁路和公路建设中被广泛使用，例如宜万铁路渡口河特大桥的最高墩128 m，黄延高速公路的洛河特大桥最高墩达143 m。文献［1］指出对于墩高超过40 m，墩身第一阶振型有效质量低于60%，且结构进入塑性的高墩桥梁应作专项研究，美国CALTRANS抗震设计规范仅适用于规则桥梁，而高墩桥梁一般都是典型的非规则桥梁［2］。

近年来，国内外学者对高层建筑结构以及高墩桥梁的抗震性能进行了很多的研究，Sasaki等［3］通过对高层框架式建筑结构的分析说明在Pushover分析中仅考虑一阶振型的加载模式是不足以去识别损伤可能出现的位置；Krawinkler等［4］指出对于受高阶振型作用显著的高层建筑结构和桥梁高墩，pushover方法并不适用，其应用受到一定条件的限制；Panagiotou等［5］对高阶振型影响下的高层建筑中墙体结构的地震反应进行了探讨，并使用双重塑性铰概念（DPH）对高层建筑中墙体结构的抗震设计提出建议。Ceravolo等［6］研究了高墩抗震设计中使用能力设计方法时应考虑的塑性铰位置，并探讨了地震动的频谱特性本身对高墩抗震设计的影响；李建中等［7-8］指出高墩的位移延性能力与地震荷载、高阶振型效应、墩身质量等有一定的关系；梁智垚［9］通过IDA方法，计算了非规则桥梁中的不同墩高墩柱的屈服位移、极限位移和位移延性能力，讨论了墩身质量和高阶振型参与对高墩墩身节点位移、截面曲率的影响。上述学者的研究都指出了高阶振型对高层建筑及桥梁高墩的地震响应有显著影响，但分析高墩桥梁的抗震性能的数据并不全面，缺乏充足的统计数据，现有的研究成果及实验数据主要是针对墩高为30 m以下的中、低墩。现行的桥墩延性能力计算方法仍然采用静力的计算方法，利用约束混凝土的应力应变关系，进行P-M-φ分析，在计算中假设墩身的曲率沿墩高线性分布，得到截面曲率延性和桥墩的位移延性能力，采用静力方法研究桥墩的延性性能很难考虑桥墩本身质量和高阶振型的贡献。对中、低墩，由于其桥墩本身质量和高阶振型贡献可以忽略，采用静力方法研究是可行的。对于高墩，由于其具有截面尺寸大、结构周期长、墩身质量大等特点，并且由于地震动输入的频谱特性本身就会影响高阶振型的贡献程度，截面曲率沿墩高的分布将呈现复杂的曲线分布，忽略桥墩自身的惯性力和高阶振型的贡献会导致较大的误差。

因此，对不同地震动输入下高阶振型对高墩桥梁抗震性能的影响进行更深入广泛的研究是有必要的。

1 地震动记录的选择

地震动记录的选取和调整对非线性时程分析的可靠性是很重要的过程，场地条件对地震波的传播又有较大的影响。场地条件对地震动的影响不仅仅表现在对地震动幅值变化上，而且还表现在对地震动频谱特性的变化上。本文按照吕红山［10］对中美两国场地分类指标的比较找出的联系，从美国太平洋地震工程中心的强震数据库中选取选用了7条震级在6.8～7.5之间的Ⅱ类场地远场地震波，各地震波记录的地震动参数见表1。

表1 地震动记录Tab.1 Ground motion records

2 计算模型及方法

墩柱计算模型采用墩底固结的悬臂梁，墩身质量堆聚在相应的节点上，将与墩柱相邻的一跨上部结构质量等效为墩顶集中质量。分别以60 m、90 m墩高，墩顶质量分别采用1 000 t和2 000 t作为4个不同的计算模型进行分析，不同模型的基本参数见表2。

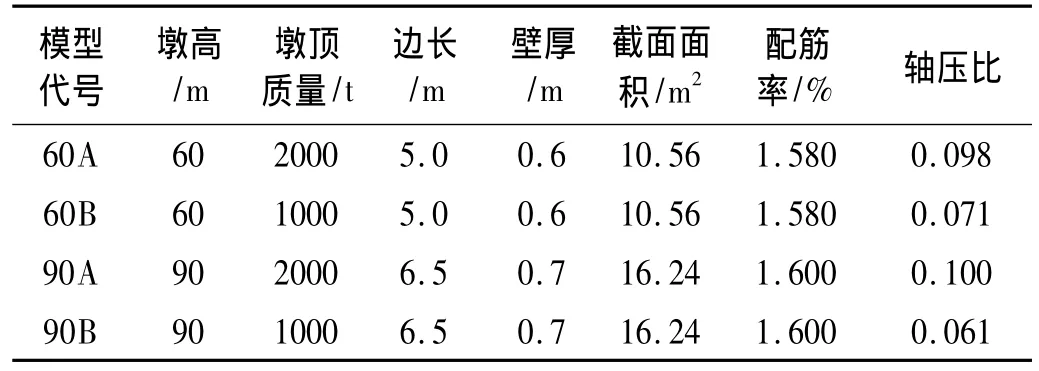
表2 墩柱基本参数Tab.2 Basic parameters of piers

本文采用OpenSees地震分析软件进行非线性静力分析和非线性时程动力分析［12］。墩柱使用纤维单元模拟，梁智垚等［11］对桥梁高墩的计算模型进行了有益的探讨，证明了在高墩抗震性能分析中采用纤维单元模型的适用性。

2.1 非线性静力分析方法

非线性静力分析起初用于结构地震危险性的快速估算，随着基于性能的结构设计方法的产生和发展，进一步得到推广和应用，ATC-40、FEMA440等规范都采用了Pushover方法。图1为使用与前三阶模态相对应的侧向力分布模式进行Pushover得到的墩底剪力Vbn和墩顶位移urn的关系曲线。本文采用与一阶振型对应的侧向力分布模式进行Pushover分析，以墩底截面曲率达到屈服曲率时的墩顶位移作为屈服位移，墩底截面曲率达到极限曲率时的墩顶位移作为极限位移。

由图1（b）可知，使用二阶振型作为侧向力分布模式的Pushover分析得出的关系曲线出现了“反向”的形状，Goel等［13］在对高层建筑进行高阶振型Pushover分析时发现这种现象，并通过基本的结构动力学和塑性理论解释了这种现象产生的原因。以90 A计算模型为例，将90 A计算模型的第二阶振型Pushover曲线以及Pushover分析中不同侧向力的墩身位移曲线绘入图2。

图1 Vbn-urn关系曲线Fig.1 Vbn-urncurves

图2 Pushover和墩身位移曲线Fig.2 Pushover and displacement curves

由图2可知，在Pushover分析的弹性阶段（点a，b，和c），墩身的变形形状和第二阶振型形状成比例。并且墩顶位移随着侧向力增加而增加，由于高墩模型按二阶振型分布的侧向力的合力为负值，当墩身在墩底塑性铰区域以上出现塑性变形机制后，侧向力就会使墩顶的运动方向与之前弹性阶段的方向相反，这就是产生图2（a）中“反向”Pushover关系曲线的原因。

2.2 IDA分析方法

目前，桥墩的延性能力计算方法还主要是采用静力的计算方法［14］，为了能够较为准确的计算墩柱延性能力，本文使用增量动力分析方法（IDA）［15］，IDA方法能够逐级施加地震动荷载来研究结构的整个损伤、破坏过程。梁智垚已经证明了由于高阶振型参与的影响，IDA分析时高墩墩顶位移最大值和墩底曲率最大值不会同时达到［9］。若某级PGA下墩底曲率达到屈服曲率，则称为“屈服曲率”，而该级PGA下墩顶的最大位移称作“屈服位移”。此外，极限状态下延性构件的极限曲率和极限位移也参照上述原则确定。为了观察结构的整个非线性阶段并较为准确地捕捉屈服状态和极限状态，使用0.01的调幅系数（Scale Factor）调整各条地震动输入进行IDA分析，记录各地震激励下高墩屈服状态和极限状态的位移延性能力。

3 计算结果及分析

3.1 MPA方法与IDA方法的位移延性能力比较

图3为采用表1中的7条地震波对不同墩柱分别进行IDA分析和MPA分析得到的屈服位移和极限位移，柱状图为IDA分析的结果，水平直线为相应的MPA方法计算结果。

由图3（a）可和，在不同地震波激励下，IDA和MPA两种方法的屈服位移计算结果差别并不相同，60 m墩在E3、E5、E7地震波激励下以及90 m墩在E3、E4、E7地震激励下，两种方法的屈服位移计算结果相差较小；墩顶质量为1 000 t的90 m墩在E1地震激励下，两种方法的屈服位移计算结果相差较小。由图3（b）可知，60 m墩在E6地震波激励下，IDA和MPA两种方法的极限位移计算结果相差较大。除了E7地震波，90 m墩在其他地震波激励下，两种方法的极限位移计算结果都有不同程度的偏差，E6地震波激励下的偏差较大。通过分析可知，当60 m墩和90 m墩在E7地震激励下达到屈服状态时，以及60 m墩在E3、E5、E7地震激励下达到屈服状态时，使用MPA方法已能够较为准确计算屈服位移。而在其他地震波激励下，使用MPA方法计算屈服位移将会产生较大偏差。而当60 m墩和90 m墩在E7地震激励下达到极限状态时，使用MPA方法也能够较为地准确计算极限位移。

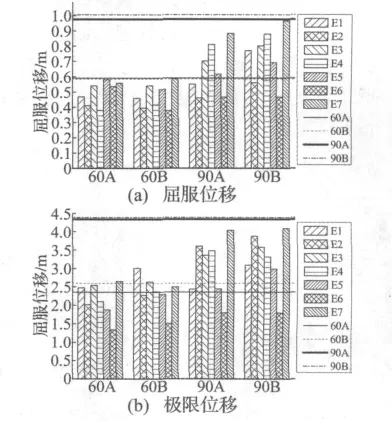
图3 屈服位移和极限位移Fig.3 Yield displacement and ultimate displacement

图4为采用表1中的7条地震波对不同墩柱分别进行IDA分析和MPA分析得到的最大位移延性能力，柱状图为IDA分析的结果，水平直线为相应的MPA方法计算结果。

图4 最大位移延性能力Fig.4 Maximum displacement ductility capacity

由图4（a）可知，在E1、E2、E4地震波激励下，60 m墩采用IDA方法计算的位移延性能力都大于MPA方法计算出的结果，因此，使用MPA方法的位移延性结果能够偏于安全的对60 m高墩进行抗震设计。而在E5和E6地震波激励下，采用IDA方法计算的位移延性能力小于MPA方法的计算结果，在这种情况下使用MPA的分析结果进行抗震设计已不能满足指定的性能目标。由图4（b）可知，在E2地震波激励下，90 m墩采用IDA方法计算的最大位移延性能力远大于MPA方法计算的结果。除了E2、E3地震波以外，IDA方法计算出的90 m墩的最大延性能力与MPA方法计算的结果相比都偏小。

3.2 MPA方法与IDA方法的墩身曲率包络比较

通过分析IDA结果可知，各地震波激励下，达到屈服状态时，墩顶质量不同对60 m和90 m墩的墩身曲率包络形状并无影响，只是数值稍有不同；达到极限状态时，除了E1地震波激励下使得60 m墩的曲率分布略有不同外，墩身曲率包络形状基本相同，且由于在实际工程中，墩顶质量偏大，故选取60 A和90 A计算模型作为研究对象，图5给出了采用7条地震波进行IDA分析，对应墩底截面曲率达到屈服曲率和极限曲率时刻的截面曲率沿墩身分布的包络曲线。为了便于比较，MPA分析得到的相应状态墩身曲率分布曲线也绘与同一图内。由于pushover分析采用了一阶振型作为侧向力分布并在加载过程中保持不变，其截面曲率均为正曲率且成倒一阶振型形状分布。

由图5（a）可知，除了E3、E5以外，60 m墩在其它地震激励下屈服状态墩身曲率包络形状与MPA分析得到的计算结果均不相同。由图5（b）可知，除了E1、E3、E4以外，60 m墩在其它地震波激励下极限状态墩身曲率包络形状与MPA分析得到的计算结果有不同程度的差别，IDA方法比MPA方法计算出的墩身曲率最大超出340%。由图5（c）可知，90 m墩在各地震激励下的墩身曲率包络在40 m墩高附近均呈现明显反向弯曲的形状。由图5（d）可知，对于90 m墩，各地震波激励下，极限状态墩身曲率包络曲线并不相同，在E2、E3、E5、E6地震波激励下极限状态墩身曲率包络在50 m墩高附近出现墩底曲率之外的大值，墩身曲率分布在中上部呈现明显凸起的形状，IDA方法比MPA方法计算出的墩身曲率最大超出614%。

通过以上对比分析可知，60 m墩在E2、E5、E7地震动激励下，90 m墩在 E2、E3、E5、E6地震动激励下，在墩底截面曲率达到极限状态时，墩身曲率会产生墩底截面曲率之外的大值，也就是说，在墩柱从屈服状态到极限状态的过程中，墩身会出现墩底之外的一个塑性铰区域。对能力保护设计而言，需要正确估计塑性铰区域的位置，而使用仅考虑一阶振型的pushover分析是无法估计桥墩在某些地震波激励下墩身出现墩底截面之外的第二个塑性铰区域。

图5 墩身曲率包络Fig.5 Pier curvature envelope

4 谱分析

为了识别高阶振型在各地震波激励下对高墩地震响应产生的影响，将墩底剪力和墩顶位移urn的关系曲线转换为谱加速度和谱位移格式。Chopra将Vbn-urnPushover曲线转换为Fsn-Dn关系［13］，转换关系如下：

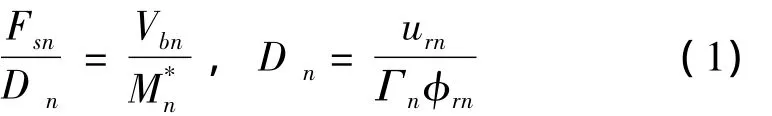
根据IDA分析的结果，将阻尼比为5%的7条地震动调整至对应分析结果屈服和极限的水平，并将其反应谱转换为ADRS（Acceleration-Displacement Response Spectrum）格式，与已经转换为谱加速度和谱位移关系的Pushover曲线绘制入图7，这里只是要观察墩柱各阶模态在不同地震动激励下进入塑性的程度，因此直接使用了弹性反应谱。限于篇幅，只列出90 A的分析图形。

图6 Fsn-Dn关系曲线Fig.6 Fsn-Dncurves

图7 A-D格式反应谱与墩柱能力谱Fig.7 Demand diagram and capacity diagram in A-D format

图7（a）给出了屈服水平下一阶和二阶pushover的能力谱关系曲线，在地震动激励下墩底截面达到屈服曲率时，90 m墩柱一阶振型都已经进入塑性，而二阶振型在多数地震波激励下仍保持弹性；图7（b）给出了极限水平下二阶和三阶pushover分析的能力谱关系曲线，在地震波激励下墩底截面达到极限曲率时，90 m的一阶、二阶振型都进入了塑性，而三阶振型在多数地震波激励下仍保持弹性。由于高墩弹性阶段后的变形和损伤位置将会受到进入塑性的高阶振型的影响，对照图5，可知二阶振型是桥墩从屈服状态到极限状态过程中墩身出现塑性铰的主要原因。并由图7可知，在高墩的抗震性能的分析中，屈服状态和极限状态下墩柱高阶振型贡献的程度受到地震波自身频谱特性的影响，各地震波输入下屈服状态和极限状态的高阶振型进入塑性的程度并不相同，因此，将中、低墩中不考虑高阶振型和地震波自身频谱特性的静力计算方法应用于高墩的位移延性能力的计算中是不适当的。

5 结论

通过选取7条Ⅱ类场地地震波并使用基于一阶振型的非线性静力推倒方法（MPA）和增量动力方法（IDA）对高墩的屈服位移、极限位移、位移延性系数以及墩身曲率分布进行分析和探讨，结果表明：

（1）高墩在Ⅱ类场地的不同地震动激励下达到屈服状态和极限状态时，由于高阶振型的参与程度不同，导致采用两种方法计算屈服位移和极限位移以及最大位移延性能力的结果差别不同，MPA方法的计算结果只在个别地震动激励下适用。

（2）对于高墩，在所选Ⅱ类场地不同地震动激励下，两种方法估计的墩身屈服曲率的包络以及极限曲率的包络都有不同程度的区别，由于高阶振型对不同地震波激励的敏感性不同，部分地震动激励下，墩身极限曲率的包络会出现墩底曲率之外的大值，也就是说地震动激励下随着结构塑性程度的增加，可能使墩身出现墩底之外的另一个塑性铰区域。

（3）高墩的高阶振型Pushover曲线会出现“反向”的现象，这种现象只会出现在基阶振型以外的更高阶振型的Pushover曲线中，而这种现象在中低墩中是很罕见的。

（4）通过谱分析可知，在所选7条地震波的IDA分析中，当高墩达到屈服状态时，一阶振型已进入塑性，二阶振型大都保持弹性；而当高墩达到极限状态时，一阶和二阶振型都已进入塑性，而三阶振型大都保持弹性。对于高墩，二阶振型是墩身出现塑性铰的主因。

［1］JTG/T B02-01-2008公路桥梁抗震设计细则［S］.北京：人民交通出版社，2008.

［2］California Department of Transportation.Caltrans seismic design criteria version 1.5［S］.September 2009，Business Transportation and Housing Agency， State of California，2009.

［3］ Sasaki K K，Freeman S A，Paret T F.Multi-mode pushover procedure（MMP）-A method to identify the effects of higher modes in a pushover analysis［J］.Proc.of the Sixth US National Conference on Earthquake Engineering，Earthquake Engineering Research Inst，Oka.1and，California，1998：1-12.

［4］ Krawinkler H，Senevirations G D P K.Pros and cons of a pushover analysis of seismic performance evaluation［J］.Engineering Structures，1998，20（4）：452-464.

［5］ Panagiotou M，Restrepo J I.Dual-plastic hinge design concept for reducing higher-mode effects on high-rise cantilever wall buildings［J］.Earthquake Engineering and Structural Dynamics，2009，38：1359-1380.

［6］ Ceravolo R，Demarie G V，Giordano L，et al.Problems in applying code-specified capacity design procedures to seismic design of tall piers［J］.Engineering Structures，2009，31（8）：1811-1821.

［7］李建中，宋晓东，范立础.桥梁高墩位移延性能力的探讨［J］.地震工程与工程振动，2005，25（1）：43-48.

［8］宋晓东.桥梁高墩延性抗震性能的理论与试验研究［D］.上海：同济大学，2004.

［9］梁智垚.非规则高墩桥梁抗震设计理论研究［D］.上海：同济大学，2007.

［10］吕红山，赵风新.适用于中国场地分类的地震动反应谱放大系数［J］.地震学报，2007，29（1）：67-76.

［11］梁智垚，李建中.桥梁高墩合理计算模型探讨［J］.地震工程与工程振动，2007，27（2）：91-98.

［12］ Silvia M，Frank M，Michael H.Open system for earthquake engineering simulation user manual［M］.Berkeley：Pacific Earthquake Engineering Research Center，University of California，2007.

［13］ Goel R K，EERI M，Chopra A K.Role of higher-“mode”pushover analyses in seismic analysis of buildings［J］.Earthquake Spectra，2005，21（4）：1027-1041.

［14］ Priestley M J N，Seible F，Calvi G M.Seismic design and retrofit of bridges［M］.New York：John Wiley＆Sons，1996.

［15］ Dimitrios V C，Allin C.Incremental dynamic analysis［J］.Earthquake Engineering and Structural Dynamics，2002，31：491-514.