空间热载荷作用下星载天线耦合动态影响分析

游斌弟，赵志刚，李文博，赵 阳

（1.哈尔滨工业大学（威海）船舶与海洋工程学院，威海 264209；2.哈尔滨工业大学 航天学院，哈尔滨 150001）

星载天线是依附在卫星上用来实现运动指向的空间机构，广泛应用于国外数据中继卫星和通信卫星［1］。2003年中国航天科技集团在中星22上首次采用了自主研发的偏馈双反射面Ka可移点波束天线，实现了卫星天线的定位跟踪运动［2］。

天线结构暴露在外层空间，长期经受太阳辐射、深冷空间周期性作用，引起温度剧烈变化，会在反射器的正面与背面产生不均匀的温度变化。随时间变化的温度梯度，使得天线工作产生较大的热变形或热振动，导致天线指向精度严重下降，无法正确接收或发送信息和指令，甚至引起航天器在轨姿态变化［3-4］，为此，本文考虑空间热载荷作用下对星载天线动态影响。

目前，研究温度与变形相互耦合的热弹动力学方法较为成熟。Sundaresan［5］应用非线性应变位移关系，分析了温度时变规律已知情况时，得到热弹耦合结构刚度矩阵；Wu［6］基于梁变形的线弹性假设，研究了热载荷作用下柔性梁的动力学特性；Singha［7］用有限元法研究了复合材料板大范围的柔性自由振动；Ribeiro［8］研究了热载荷作用下四边固支圆柱壳在振动特性。丁勇等［9-10］构造了一种薄壁圆管温度傅里叶 -有限单元，分析了哈勃太空望远镜一块太阳能帆板的温度场和弯曲位移场和大型空间结构热-动力学耦合有限元分析；程乐锦等［11］分析复杂的空间结构给出了热动力学响应，并发现热动力学耦合效应和热诱发振动稳定性的决定因素是结构参数及加热条件。然而上述研究都局限与结构动力学问题，为了进一步研究在热载荷作用下作大范围运动的多体系统动力学问题，Johnston［12］研究了在温度时变规律已知的情况下太阳能帆板的刚-柔耦合动力学特性，但没有考虑非线性效应；Saniei［13］考虑了几何非线性效应，研究了非均匀温度分布的高速转子的频率特性；Oguamanam［14］建立了热流作用下中心刚体-薄板的刚柔耦合系统的动力学模型，研究了运动过程中的非线性效应。刘锦阳等［15-17］从非线性应变-位移关系式出发，用虚功原理建立了热载荷作用的柔性梁/板的热传导方程和旋转刚体-梁系统的刚柔耦合动力学方程。然而，目前考虑热载荷因素只局限于单个物体的刚柔耦合动力学分析，未能推广到多体系统中，尚未建立热载荷情况下壳体的刚柔耦合多体动力学模型。

针对以上情况，本文根据天线反射面的几何特性，采用离散化的壳体单元，考虑壳体温度沿厚度方向变化，推导了有限元离散化的热传导方程。在此基础上，从应变应力关系出发，利用拉格朗日方程推导了热载荷作用下大范围运动的星载天线刚柔耦合动力学方程，研究了热冲击作用下柔性反射面形面变形和系统的刚柔耦合动力学特性的影响，为进一步提高天线的指向精度奠定理论基础。

1 反射面有限元离散化热传导方程

星载天线在轨运行时承受着时刻变化的热载荷，对于在轨的某一时刻，由于卫星本体姿态及天线指向的不同受到不同的热载荷，且热载荷不均匀造成温度分布不均衡，导致变形受到约束，引起热应力的产生。根据天线抛物反射面的材料特性和几何特点，基于薄壳壳体有限元单元法对抛物反射面进行温度场分析，为星载天线刚柔耦合动力学建模的提供理论基础。

1.1 几何描述

天线反射面是由二次曲线旋转产生，其厚度远小于口径尺寸，可认为薄壳结构，利用壳体单元对反射面进行离散化，如图1所示，为了较准确地描述反射面的几何形状，将（ξ，η）定义为反射面上的自然坐标，ζ为厚度方向坐标，且-1≤ξ≤1，-1≤η≤1，-1≤ζ≤1。因此，壳体内任意一单元的变形坐标列阵δ可近似表示为：

图1 反射面壳体单元描述Fig.1 Shell element description of antenna reflector

或写成：

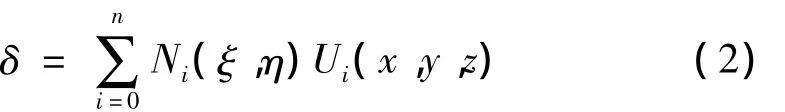
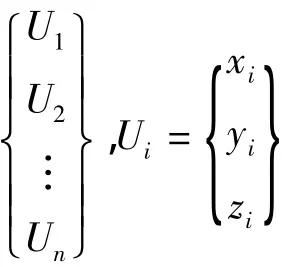
1.2 热弹性方程

对于连续抛物面薄壳壳体，材料为各向同性，根据基尔霍夫-勒夫的切面应力假设，其法向应力为零，横向位移独立于厚度，σz=0，τxz=τyz=0，则应变和应力列阵ε、σ分别为：

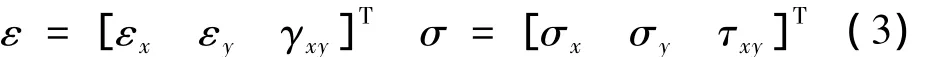
满足本构关系：

式中：

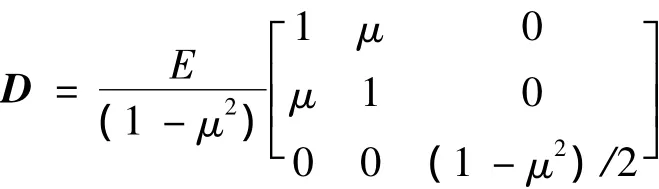
其中E和μ分别为材料的弹性模量和泊松比；ε0为温度变化引起的热应变，可表示为：

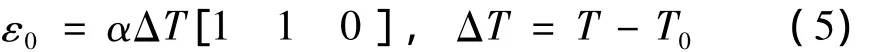
式中：α为热膨胀系数；T和T0分别为柔性反射面上任意一点的温度和参考温度。在线弹性假设下，应变与变形的关系式为：

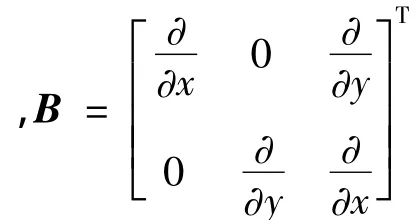
1.3 有限元离散的热传导方程

在空间环境下，星载抛物反射面内部产生较大的温度变化，其温度在反射面厚度方向上呈现非线性变化，如图1所示。因此，在厚度方向上采用二次函数g（ζ）进行插值，每个节点有3个自由度，分别反应反射面正面s1、中面s2和背面s3的温度T1、T2和T3，则任意一单元温度T为：

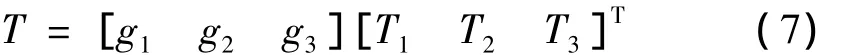
其中：

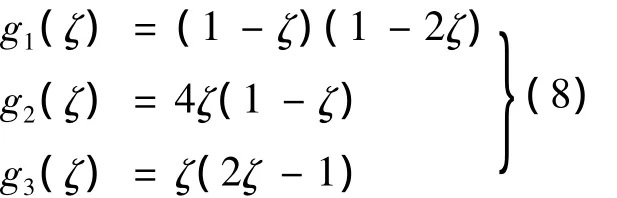
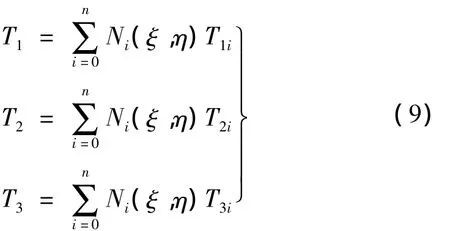
或者写成：

式中：［N'］=［g1g2g3］［N1N2…Nn］，{T}e为单元温度列阵。

则任意一单元平均温差ΔT为：

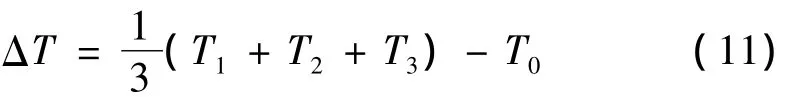
根据伽辽金法，可得单元内的加权积分的瞬态热传导方程为：

由于天线在轨道上绕地球运动时，受到太阳热流载荷S0的作用，设S0的方向与反射面的夹角为γ，如图2所示，γ随着天线指向位置变化而变化。则反射面上任一微元ds受到的太阳辐射外热流q可表示为：

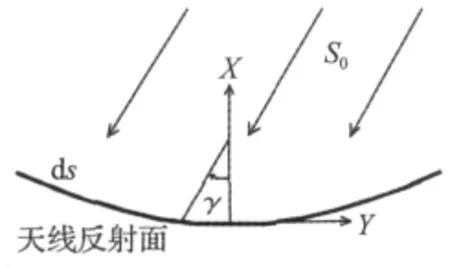
图2 太阳辐射外热流Fig.2 External thermal flux of solar radiation

式（12）按单元有限元方程进行集成，得到整体温度场的微分方程：

其中：C、KT、RT和F分别为整体热容矩阵、热传导矩阵、热辐射矩阵和热载荷矩阵。

2 星载天线刚柔耦合动力学建模

在星载天线动力学建模中，作如下假设：

（1）卫星本体为漂浮基座；

（2）星载天线机构（除了反射面）视为刚体；

（3）关节驱动不考虑间隙非线性影响；

（4）反射面与天线转轴末端刚性连接在一起；

（5）不考虑太空微重力作用影响；

（6）柔性反射面发生小变形，其弹性变形可认为线性变形。

根据模型假设，建立旋转关节轴线为z方向，绕z轴转动，旋转角为θ1，θ2，天线转轴末端坐标系∑e；建立惯性坐标系∑0、本体坐标系∑B和各关节坐标系∑i，其中本体坐标系∑B中x轴为滚动轴，y轴为俯仰轴，z轴为偏航轴（如图3）。在关节坐标系{∑i}中，原点固定在关节i，轴固结在关节坐标系{∑i}的原点，关节i均为理想约束。

图3 星载天线的动力学模型Fig.3 Dynamic model of satellite antenna

由图3可知，柔性反射面未变形A点，当发生热弹性变形δ时变为A'点，假设反射面的弹性变形量小于其壁厚的1/10，可认为是线性变化。

下面将对系统能量和外载荷描述，利用柔性反射面的离散化单元信息，建立考虑热载荷的星载天线耦合动力学模型。

（1）卫星本体和转轴的动能Tbm和势能Vbm：

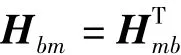
（2）柔性反射面动能Ta：

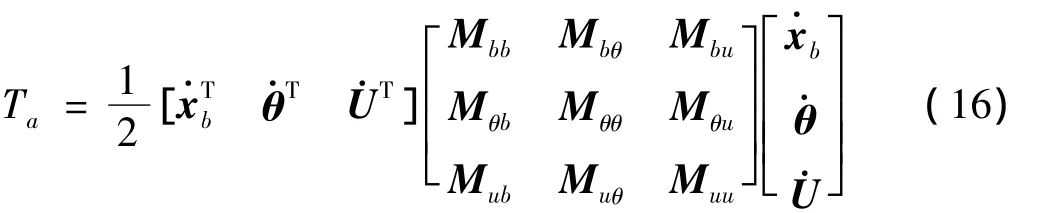
式中：Mjk（j=b，θ，u；k=b，θ，u）的具体表达式见文献［18］。

（3）热弹性变形引起柔性反射面势能Va：

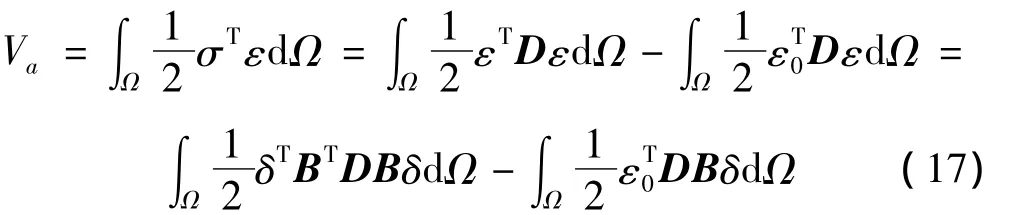
由式（1）、式（5）和式（17），可知，非线性耦合弹性刚度阵Ku和热弹性力FT分别为：

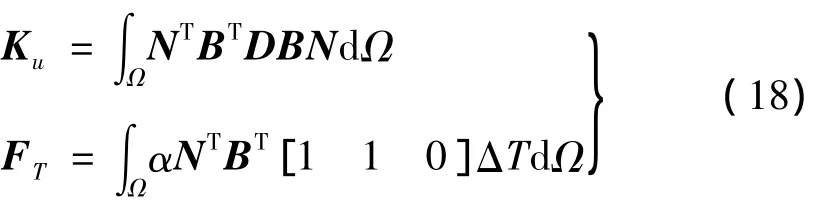
最后利用Lagrange方程，得出整个星载天线的动力学方程：

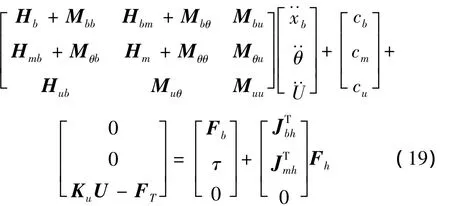
式中：cb，cm，cu分别为卫星本体、转轴、柔性反射面模态坐标的速度非线性项；Fb，τ分别为卫星本体控制力/力矩及转轴关节控制力矩；JTbh为转轴末端相对卫星本体雅可比矩阵；JTmh为转轴末端相对关节雅可比矩阵；Fh为外力/力矩。

3 空间热载荷对星载天线影响分析

星载天线机构由卫星本体、天线转轴、反射面以关节旋转铰链接而成，其中天线刚性连接在天线转轴末端上（如图3）。主要物理参数见表1（国际单位），每个刚体质心在其几何中心ai=bi=0.5。

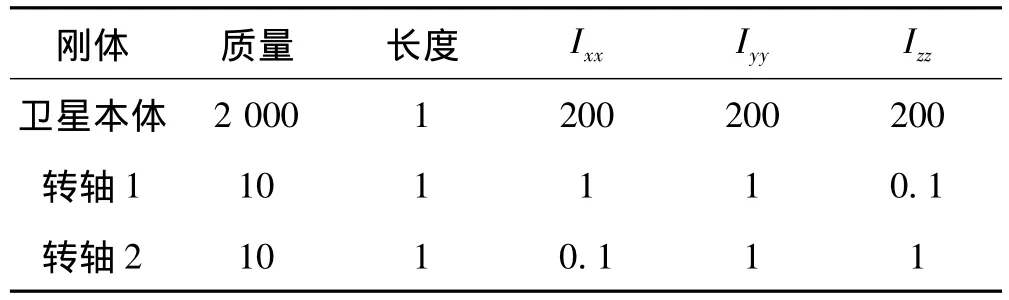
表1 星载天线机构物理参数Tab.1 Parameters of satellite antenna

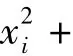
初始参数：卫星本体位置及速度均为0；转轴关节角θ1=θ2=0，各关节速度均为0，卫星本体控制力/力矩Fb和外力/力矩Fh均为0，关节力矩τ1=5 N·m，τ2=10 N·m，仿真步长 0.001 s；仿真时间 5 s。

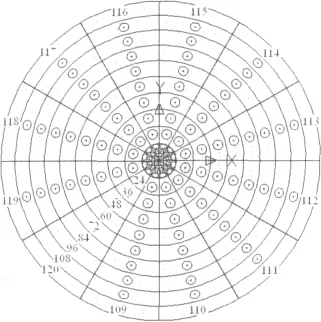
图4 反射面有限元离散化Fig.4 Finite element discretization of antenna reflector

为了方便计算，本文将天线面的节点受空间环境作用达到的温度T∞分别设定为200 K、300 K、400 K，研究这三种工况时星载天线在关节驱动力的作用下，反射面位置随着天线指向角的变化而受到不同的热载荷情况。图5为反射面壳单元110的温差变化过程，可知，随着环境温度的升高，其反射面的正面、中面和反面产生的温差呈现幅值升高。

图5 反射面壳单元110温差变化Fig.5 Temperature difference of flexible antenna reflector（Element 110）

以柔性抛物反射面的壳单元110为分析对象，如图6所示。在初始时刻关节驱动力矩τ突变启动下，激发了柔性发射面的小幅振动幅值和弹性变形，随着力矩τ的持续作用，系统的转速增大，导致非线性项cu增大，造成高频抖动；另外，在T∞为200 K、300 K和400 K的情况下，温度增高引起抛物面反射不均匀温度梯度，引起的热应变造成反射面壳体的软化效应，由图6可知，随着太空环境温度T∞增大，则非线性耦合刚度Ku的软化效应愈显著，热膨胀引起的应力增大，使得壳体的弹性变形的波动幅值越来越大，产生不稳定振动，这是由于结构变形产生瞬变热流，导致了反射面截面内的温度梯度，引起了动态的温度载荷，与结构变形发生耦合，诱发耦合颤振。

图6 柔性反射面（单元110）弹性变形量Fig.6 Elastic deformation of flexible antenna reflector（Element 110）

为了分析柔性反射面对天线转轴指向的影响，如图7至图9所示，分别考虑T∞为200 K、300 K和400 K的情况下，天线转轴沿着θ1、θ2运动。由图7可知，由于转轴末端与反射面固结，天线转轴指向直接受到反射面弹性变形的影响，在指向过程初期，发生小幅值扰动，此时曲线基本重合，即天线工作初期温度增高引起的热膨胀对系统的动态特性影响很小。经过1.5 s后，随着角速度的增大，其震荡幅值变大，说明热效应对整个系统的动态特性有着显著的影响。由图8、图9可知，扰动幅值小，频率低，对天线转轴角速度和指向角将产生稳态偏差，随着驱动力矩和热载荷的持续作用，其天线指向角偏差越来越大，t=5 s时，T∞=200 K与400 K 产生的θ1偏差为 0.927 deg，θ2偏差为 -0.775 deg，严重降低了天线指向精度，因此空间热效应对天线指向精度影响不可忽略。

如图10至图12所示，分别考虑T∞为200 K、300 K和400 K的情况下卫星本体的姿态运动，由图10可知，由于卫星本体的质量相对于其它部件质量大的多，考虑热效应的反射面扰动对卫星本体的影响较小，但呈现相应的波动差异，发生小幅的低频抖动。由图11、图12可知，由于温差引起的热载荷作用在反射面上，产生的作用很小，且其姿态角和角速度为光滑曲线，说明反射面的热效应对卫星本体的角速度和姿态角影响不大，但随着时间的持续作用，其卫星姿态角偏差将变大。

综上所述，在不同的空间热环境下，反射面随着指向位置的变化产生不均匀的温度梯度，进而产生热应力、热变形；在关节驱动力和热载荷耦合作用下，激发柔性反射面震荡，引起了自身的弹性振动，其弹性振动进而又影响了整个星载天线的动态性能，因此，研究大范围运动的星载天线动力学特性，必须考虑柔性反射面热效应与弹性变形的耦合作用。

4 结论

（1）根据天线抛物反射面薄壳特点，从应力-应变关系出发，利用壳体单元的有限元离散化，考虑壳元厚度方向温度变化，且其厚度方向上采用二次函数进行插值，推导了反射面各个单元瞬态温度有限列式，并结合热弹性动力学理论，建立了反射面热传导方程；

（2）考虑星载天线的热效应因素，利用反射面的应变能表达式并结合拉格朗日法建立大范围运动的刚柔耦合星载天线的多体动力学方程，研究了温度载荷引起的非线性耦合弹性刚度阵Ku和热弹性力FT变化对星载天线的动力学特性影响很大，其热弹耦合效应不能忽视；

（3）考虑了空间环境的热效应，对漂浮基星载天线系统进行动力学分析，结果表明，随着温度梯度的增大，引起了动态的温度载荷，与结构变形发生耦合，诱发耦合颤振，加剧柔性反射面的弹性振动，使得反射面与天线转轴、卫星本体的速度非线性耦合作用变大，其抖动的频率和幅值变大，造成卫星姿态和天线指向的扰动，严重降低了星载天线的指向精度。

［1］赵 阳，白争锋，王兴贵.含间隙卫星天线双轴定位机构动力学仿真分析［J］.宇航学报，2010，31（6）：1533-1539.

［2］孙 京，马兴瑞，于登云.星载天线双轴定位机构指向精度分析［J］.宇航学报，2007，28（3）：545-550.

［3］Chung P W，Thornton E A.Torsional buckling and vibrations of a flexible rolled-up solar array［A］.AIAA，1995：1654-1664.

［4］Murogona M，Thornton E A.Buckling and quasistatic thermal-structural response of asymmetric rolled-up solar array［J］.Journal of Spacecraft and Rockets，1998，35（2）：147-155.

［5］Sundaresan P，Singh G，Venkateswara Rao G.A Simple approach to investigate vibratory behavior of thermally stressed laminated structures［J］.Journal of Sound and Vibration，1999，219（4），603-618.

［6］Wu G Y.Transient vibration analysis of a pinned beam with transverse magnetic fields and thermal loads［J］.ASME Journal of Vibration and Acoustics，2005，127（3），247-253.

［7］ Singha M K，Nonlinear vibration of symmetrically laminated composite skew platesby finite elementmethod［J］.International Journal of Non-linear Mechanics，2007，42（9）：1144-1152.

［8］ Ribeiro P.Non-linear vibrations of laminated cylindrical shallow shells under thermomechanical loading［J］.Journal of sound vibration，2008，315（3）：626-640.

［9］丁 勇，薛明德.辐射换热条件下空间薄壁圆管结构瞬态温度场、热变形有限元分析［J］.宇航学报，2002，23（5）：49-56.

［10］丁 勇，薛明德，姚海民.空间薄壁管结构瞬态温度场、热变形有限元分析［J］.应用力学学报，2003，20（1）：42-48.

［11］程乐锦，薛明德.大型空间结构热动力学耦合有限元分析［J］.清华大学学报（自然科学版），2004，44（5）：681-688.

［12］ Johnston J D，Thornton E A.Thermally induced attitude dynamics of a spacecraft with a flexible appendage［J］.Journal of Guidance，Control and Dynamics，1998，21（4）：581-587.

［13］ Saniei N，Albert C，Luo J.Thermally induced nonlinear vibrations of rotating disks［J］.Nonlinear Dynamics，2001，26（4）：393-409.

［14］ Oguamanam D C D，Hansen J S，Heppler G R.Nonlinear transient response of thermally loaded laminated panels［J］.Journal of Applied Mechanics，2004，71（1）：49-56.

［15］刘锦阳，袁 瑞，洪嘉振.考虑几何非线性和热效应的刚-柔耦合动力学［J］.固体力学学报，2008，29（1）：73-77.

［16］刘锦阳，袁 瑞，洪嘉振.考虑热效应的柔性板的刚-柔耦合动力学特性［J］.上海交通大学学报，2008，42（8）：1226-1237.

［17］刘锦阳，崔 麟.热载荷作用下大变形柔性梁刚柔耦合动力学分析［J］.振动工程学报，2009，22（1）：48-53.

［18］游斌弟，赵志刚，赵 阳.柔性天线面对漂浮基星载天线扰动分析及抑制［J］.航空学报，2010，31（12）：2348-2356.