混合结构时程分析中的阻尼比计算研究

周国伟，张志强，李爱群，徐金军

(1.东南大学 土木工程学院，南京 210096;2.广州市设计院，广州 510620;3.东南大学 混凝土及预应力混凝土结构教育部重点实验室，南京 210096;4.国内贸易工程设计研究院，北京 100001)

混合结构时程分析中的阻尼比计算研究

周国伟1，2，张志强1，3，李爱群3，徐金军4

(1.东南大学 土木工程学院，南京 210096;2.广州市设计院，广州 510620;3.东南大学 混凝土及预应力混凝土结构教育部重点实验室，南京 210096;4.国内贸易工程设计研究院，北京 100001)

混合结构由于其建筑及功能上的种种优点，在现代建筑中得到广泛应用。对这类结构进行分析时，主要有两个问题：一是在考虑不同材料的情况下，结构的整体阻尼比如何计算;二是在整体阻尼比的计算结果下，如何针对小阻尼材料进行修正。以高楼顶加钢塔的这一混合结构形式为例，建立一种非比例阻尼矩阵的构造方法，计算结果表明该构造方法得到的振型阻尼比可以较好的反映对主体结构和顶部钢塔影响最大的4阶振型的耗能特点。此外，基于反应谱法推导了顶部钢塔在整体阻尼比(第一阶主振型的阻尼比)计算下的误差，在此基础上，给出了相应的修正公式，最后采用上述方法分析了洛阳某高层顶部钢塔的地震响应。

混合结构;非比例阻尼;阻尼比;高阶振型

阻尼比是结构动力分析的基本参数，对结构动力分析结果的可靠性和精度有很大影响。对于由同种材料组成的结构，目前公认的是阻尼比处于某一范围。我国规范规定混凝土结构阻尼比取0.05，钢结构取0.02。而组合结构的阻尼比确定方法却没有统一的认识，我国《高层混凝土结构技术规程》［1］建议取0.04计算，众多试验验证了该取值具有一定代表性。但是，在高阶振型下，该取值显然不能反映结构的耗能特性。以建筑楼顶加建钢塔的结构为例，高阶振型很可能主要表现为钢结构部分的局部振动，该振型的阻尼比应该是接近钢结构的阻尼比。Newmark等［2］根据对原型和模型的实测数据，建议在原子能电站设计中，按不同结构和不同内力采用不同的阻尼比。此外，结构阻尼比还和结构的频率、响应相关。Hart等［3］根据1971年San Fernando地震中的12栋高层房屋的强震破坏记录，用傅氏变换对前三阶阻尼比进行识别，得出地面运动越强，阻尼比越大的结论。这批结构在地震中，钢结构阻尼比最大为11.3%，最小为1.5%;钢筋混凝土结构阻尼比最大为16.5%，最小为1.5%。Celebi［4］搜集了美国旧金山5栋建筑在1989年Loma Prieta earthquake(强震)作用下建筑的实测数据和低幅振动的阻尼数据，分析表明强震下，结构的阻尼比明显大于低幅值振动中的阻尼比，约为低幅值震动情况下的5～8倍。文献［5］考虑振幅和应力的影响，基于复阻尼理论采用流固耦合动力方程对某深水钢柱墩进行分析，结果表明，考虑耦合效应后，结构动力响应明显增大。在采用软件进行时程分析时，常采用基于振型的积分形式，这种积分形式需要指定结构某一振型的阻尼比。如能合理确定结构的各振型阻尼比，使该振型阻尼比能较好地反映该阶振型各不同材料的耗能的关系，其计算结果应该可信得多。文献［6－9］介绍了一种非比例阻尼矩阵的构造方法，主要思路是用各子结构的比例阻尼矩阵组装成非比例阻尼矩阵。本文基于该方法，考虑公共边界，通过自编程序，集成了更精确的阻尼矩阵，用于混合结构阻尼比的计算［10］。

在屋顶上加建钢结构塔或网架等，受到的是经过主体建筑放大后的地震作用，在交界处形成刚度和质量的突变，水平地震作用远远大于放在地面时的水平地震作用［11］，这就是“鞭梢效应”，对于鞭梢效应，目前比较认同的计算方法是在整体计算时选取足够多的振型［12］。另一种常用的设计方法是主体结构和附加结构单独计算，具有一定的随意性，且附加的钢结构在屋顶和地面下的响应不尽相同，相比之下，整体分析的结果更可信。但是，在选取足够多振型的情况下，各振型的阻尼比通常是按整体阻尼比计算的，高阶振型的阻尼比误差也会对顶端突变部位的计算结果产生较大影响。所以，进行整体分析后，有必要对上部的不利结构进行调整，用于指导设计。

1 本文非比例阻尼矩阵的构造

由前述的研究现状可知，采用各子结构的比例阻尼矩阵构造非比例阻尼矩阵是目前比较公认的一种构造方法，本文的阻尼矩阵构造亦基于此基础。按文献［6］介绍的非比例阻尼矩阵构造方法，即：

式中：C1= α1［M1］+ β1［K1］，为主结构的阻尼矩阵;C2=α2［M2］+ β2［K2］，为子结构的阻尼矩阵，C 为组合结构的整体阻尼矩阵。其中，α1、α2为质量矩阵系数，β1、β2为刚度矩阵系数;

X 表示公共边界;ωm1、ωn1、ωm2、ωn2取自整体分析计算时所得到的结构自振频率，ζ1和ζ2分别为主体结构和子结构的阻尼比。需要指出的是，在选取各阶频率时，必须反映各子结构的动力特性。对于主体结构，一般为整体分析的前两阶平动振型;对于顶部的塔楼，则需要观察振型特点，慎重选取。本文建议在构造阻尼矩阵时，所选取4个振型的频率分别为主体结构整体振动最显著的两阶振型频率和子结构局部振动最明显的两阶振型频率，这样主体结构和子结构的阻尼矩阵均能反应各自的耗能特点，由此集成的整体阻尼矩阵亦能更好地反映各阶振型的阻尼特性。

1.1 公共边界的处理方法

按本文方法构造非比例阻尼矩阵时，应先构造两个比例阻尼矩阵，然后再组合为整体阻尼矩阵。公共部分可仿造有限元整体刚度的集成方法处理。以4层混凝土－钢组合结构的层间模型为例，计算简图如图1。

图1 结构离散示意图Fig.1 The schematic diagram of the discrete structure

离散后，下部结构的质量矩阵和刚度矩阵为：

其中：［M］为结构的质量矩阵;mi(i=1，2，…)为各楼层的集中质量;ki(i=1，2，…)为各楼层的层间抗侧刚度。对于层模型，将各层的质量等效于楼层处，因此，可近似认为m12=m2;m22=0;这样，上部结构的质量矩阵和刚度矩阵为：

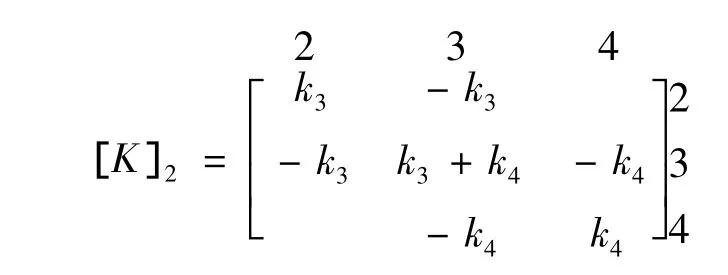
将上、下两结构在2节点处组合，即得到4层结构的整体质量矩阵和刚度矩阵。阻尼矩阵也可以按类似的方法集成。上、下部子结构在组合时，其在公共节点处所乘的系数不一致，以图1表示的模型为例，集成后的阻尼矩阵为：

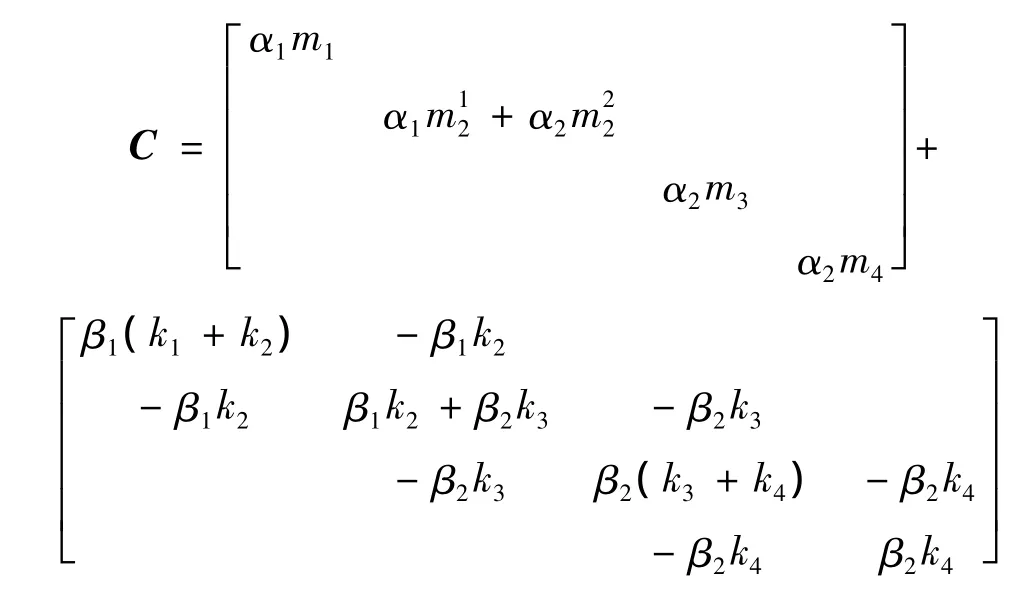
可见，在公共节点处，体现质量矩阵和刚度矩阵的主对角元素分别为+、β1k2+ β2k3;该模型只是简单的层模型，实际结构的模型公共节点可能错综复杂，因此，在组合非比例阻尼矩阵时，对于刚度矩阵和质量矩阵应先在各单元先乘以各自材料的组合系数(α、β)值，然后再集成。由于公共边界的存在，严格意义上并不能写成文献［6］中的分块形式。

1.2 结构振型阻尼比的计算

本文推荐采用阻尼比的定义计算公式(2)计算结构的振型阻尼比：

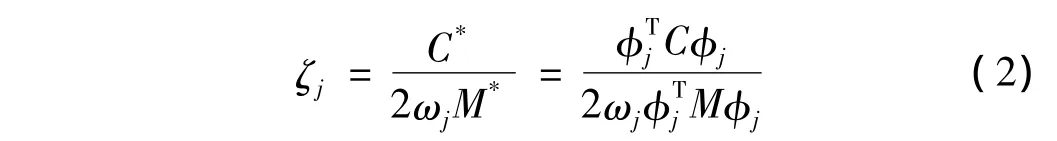
式(2)中，ζj为结构第 j振型的阻尼比;φj为结构第j振型的振型向量;ωj为振型的圆频率;C、M为结构的阻尼矩阵和刚度矩阵。由于是定义式，不论是比例阻尼或是非比例阻尼，式(2)都是适用的。对于比例阻尼体系，当按式(1)定义阻尼矩阵时，对于指定的两阶阻尼比，ζi=ζ，其他振型的阻尼比和频率有如下关系：

由式(3)可见，若选取的结构前两阶主振型构造阻尼矩阵，结构的高阶振型阻尼比随频率增高而增大。因此，在构造阻尼矩阵如只取两阶振型确定 α1、β1、α2、β2(假设取整体平动的前两阶)，会导致高阶局部振型阻尼比偏大，计算结果偏不安全。基于上述原因，本文推荐按式(2)计算振型阻尼比按下列步骤操作：

(1)采用有限元分析软件ANSYS对整体结构、下部混凝土主结构和上部的钢结构进行模态分析。提取结构刚度和质量信息文件name.full。

(2)采用FORTRAN语言对name.full文件进行编译，可从该文件中提取出质量矩阵和刚度矩阵，以压缩格式存储为Nx3的矩阵形式，其中，前两列为元素在矩阵中的行号和列号，第三列为元素值。需要注意的是，对于上部附属钢结构进行单独模态分析时，不能约束住其公共节点，以便得到完整的上部子结构的刚度矩阵，用于组装。

(3)将前面所得到的两个刚度矩阵进行组合。得到结构的整体刚度矩阵。这个过程需要通过程序实现［7］。

(4)结构的整体质量矩阵也可以由相同方法得到;

(5)对得到的各子结构的质量矩阵和刚度矩阵乘以阻尼矩阵的组合系数，将乘以系数后的分块质量矩阵和分块刚度矩阵集成为整体阻尼矩阵的质量部分和刚度部分，再将二者相加，得到整体阻尼矩阵;

(6)由得到的整体阻尼矩阵、整体刚度矩阵和整体模态分析得到的位移向量，采用式(2)计算结构的振型阻尼比。

1.3 顶部突变结构在整体阻尼比计算下的修正方法

研究

振型分解反应谱法是目前常用的结构设计计算方法。常用的结构设计软件在计算时，要求输入结构的整体阻尼比，通常该阻尼比取结构的第一阶振型的阻尼比。按SRSS方法计算的结构内力可表示为：

式(4)中：FEK表示水平地震作用标准值;Fj=αjγjXG，表示第j振型计算下的地震作用标准值，其中，αj为j振型的地震影响系数，γj为j振型的振型参与系数，X为j振型的水平相对位移，G为计算节点的质量。

从式(4)可以看出，某一振型阻尼比的取值误差对振型分解反应谱法的计算结果影响主要体现在两个方面：

(1)阻尼比取值误差造成了地震影响系数α的计算误差，从而导致该振型的下的内力计算产生误差;

(2)结构内力是各振型内力计算结果的SRSS或CQC组合，因此，某一振型的计算结果产生误差后，对整体计算结果的影响还要体现在其在参与组合时的权重。

顶端柔性子结构的地震响应主要取决于高阶振型，如不能取反映高阶振型的阻尼比，就会造成顶端柔性结构部位的计算误差。在这种情况下，如只输入结构的整体第一阶阻尼比，就应针对高阶振型对柔性部位的计算结果进行修正，使计算结果更符合真实情况。

设第k，k+1阶振型对柔性部位影响比较大，需针对该阶振型对顶端进行修正。该阶振型在精确确阻尼比计算下的影响系数为αk、αk+1，而在整体阻尼比计算下的影响系数统一为α，则第k阶振型的地震力产生的误差为(第k+1阶同)：

式(5)中：γj为第j振型的振型参与系数;Xji为第j振型向量第i自由度的值;Gi为第i自由度的重力荷载代表值;将式(5)在第k阶、k+1阶振型的地震力Fk、Fk+1处泰勒展开，并忽略高阶小量，可得：

将式(5)代入式(6)中，可得到在整体阻尼比α计算下的相对误差：

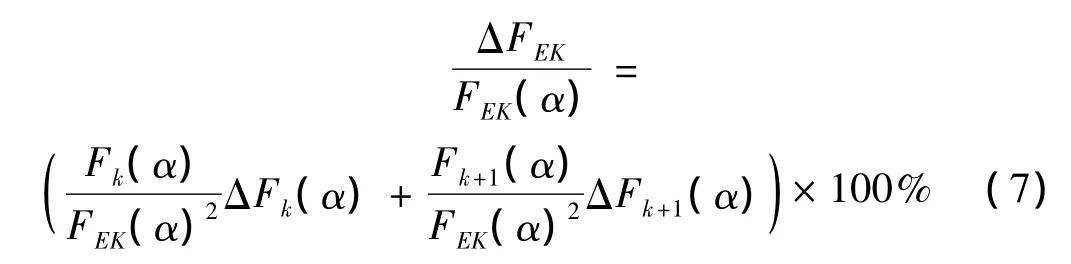
令 ：αk=(1+lk)α，lk为第k阶振型地震影响系数分别按精确阻尼比与按整体阻尼比计算之间的误差，该值从地震影响系数的角度体现了阻尼比取值误差的大小。

若需要对多阶振型进行修正，则可计算多个ηk值，从而，结构在整体阻尼比计算下的修正结果可表示为：

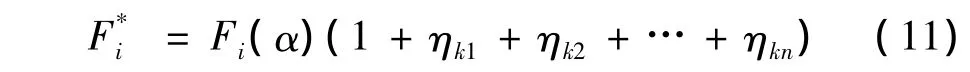
在实际计算中，通常只需要对影响大的少数几阶进行修正即可。

从式(11)中可以看出，当高阶振型表现为顶端突变结构的局部振动时，βk在振型组合中占了相当大的比重，修正系数ηk就较大;主体的βk在高阶振型下是通常非常小，主体结构部位计算得到的修正系数ηk就小。所以通常只针对顶端不利部位进行修正。本文对不同阻尼比下的反应谱进行统计分析，计算了不同阻尼比下各反应谱的之间的差值(见表1)，按0.01分段，同一区间内可按线性插值处理。

表1 阻尼比每相差0.01对α值的计算误差Tab.1 The error in α with each difference of 0.01 in damping ratio

从表1可以看出，按振型分解反应谱法计算时，假设阻尼比在0.02～0.05之间，那么阻尼比取值造成某一振型的计算误差最大约为30%。再乘以该阶振型在组合中的权重βk即可得到修正系数。

综上所述，对于顶端突变的结构，在计算分析中主要要注意两点：

(1)选取的振型一定要包括能体现对顶端突变部位的某几阶高阶振型。若未包含这些振型，计算结果将不可信，更不用谈如何修正。

(2)在选取了合适的振型后，考虑整体阻尼比对不利部位的影响，按式(11)计算得到修正系数，对顶部部位乘以相应的放大系数。

2 实例计算

采用前述的研究方法，本文计算了洛阳某大楼的振型阻尼比，并对其进行弹性时程分析。时程分析中的振型阻尼比分别采用按整体阻尼比统一指定和按各振型阻尼比分别指定，采用本文的修正方法对整体阻尼比计算下的计算结果进行修正，与按各振型分别指定的计算结果对比。由于弹性时程分析的积分方法也采用基于模态的积分，结果表明，本文的修正方法计算得到的修正系数对与时程分析也具备一定的参考价值。

2.1 算例简介

主体为钢筋混凝土结构高层建筑，在顶部标高124.02 m以上设有四个钢格构塔(平面上位于矩形平面的四个角上，对称布置)，用于安装通讯发射设备或者为了取得更好的建筑效果。钢塔分为13层，平面三角形，由三根柱支撑，总高度45 m。钢塔下部七层设有斜撑，上部五层无斜撑，顶部为单根竖杆。结构有限元模型见图2。从结构形势上看，顶部钢塔高度达45 m，与主体结构相比，刚度与质量的突变非常大，所以，该结构的模态中应该存在大量的以钢塔振动为主的振型。并且，在顶部钢塔非常柔的情况下，有些振型是只表现为顶端钢塔的局部振动。有限元的模态分析也证明了这一点。该结构多阶局部振型的周期很接近，所以，在构造阻尼矩阵时，可以在这些振型中选取计算频率，确定钢塔部分的质量矩阵系数和刚度矩阵系数。计算软件采用etabs有限元分析软件。

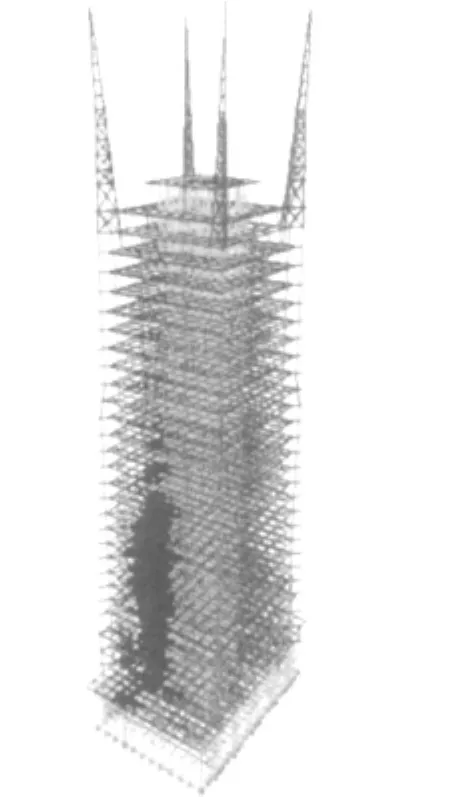
图2 结构有限元模型Fig.2 The finite element model of the structure

2.2 分析结果的比较

按本文的方法计算得到的前二十阶阻尼比见表2，图3为结构部分振型示意图。

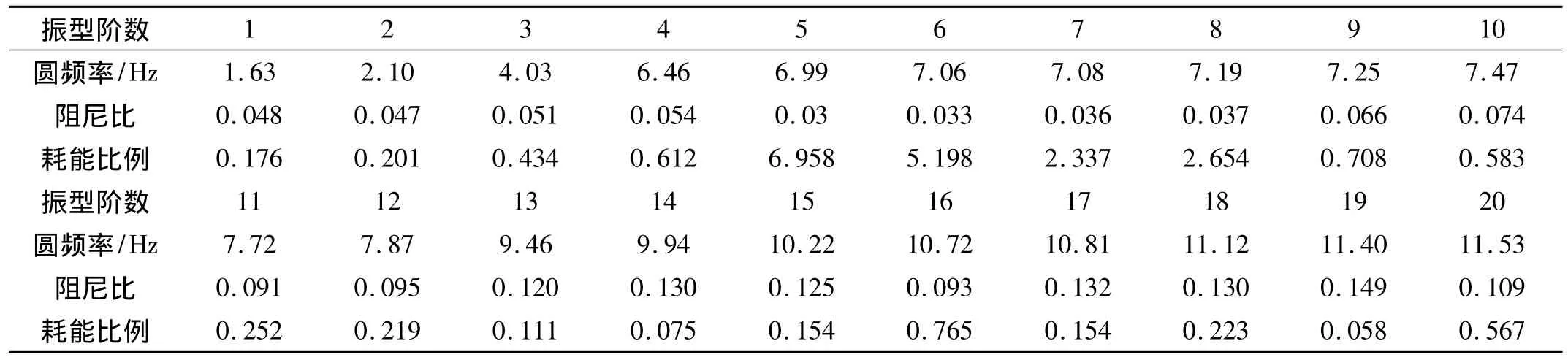
表2 结构前二十阶振型阻尼比Tab.2 The damping ratios of the models before 20

图3 1000号大楼振型示意图Fig.3 The vibration models of the No.1000 tower

结合表2和图3可看出，该结构的前两阶振型为整体平动振型，结构整体耗能以下部混凝土结构为主;第五振型至第八振型中，上部钢塔楼的独立振动现象非常明显，底部混凝土结构位移非常小，在表2中，这些振型的阻尼比基本上在0.03左右，该取值可以反映这些振型的耗能特点。

为验证高阶振型的阻尼比对突变部位的影响，对本结构分别按①所有振型阻尼比0.048;②除第5～8振型阻尼比按表2中的取值外，其余振型阻尼比取0.048两种方法进行时程分析，提取钢塔顶部的位移时程进行对比。地震波选取Elcentro波，峰值调整至35 gal，计算时间取20 s。两种方法计算得到的顶点位移时程见图4。

本文针对局部振动的前三阶振型(第五阶～第八阶)进行修正，βk采用(6)，建立层间模型提取各振型的层间位移进行估算，lk通过表2对照表1通过插值法计算。第五阶～第八阶各参数计算结果见表3。

图4 结构顶点位移时程对比Fig.4 The comparison of displacement time histories at the top point

表3 结构5～8阶修正系数Tab.3 The correction coefficient of the 5th～8thmodels

按式(11)计算得到的修正系数1+η5+η6+η7+η8=1.25，结合图4可以看出，按整体阻尼比计算和按振型指定计算得到的顶点位移最大值分别为95 mm和125 mm，即按振型指定的阻尼比计算比按整体阻尼比计算的峰值大31.6%，略大于本文的误差值25%。由于本文的修正方法是基于反应谱得到，用该方法对时程分析结果进行修正，给出修正系数并不十分精确。但从计算结果上看，本文的修正方法已具备很高的参考性。此外βk是各阶修正系数取值的重要参数，有待于计算程序的进一步发展和研究。从本算例也可以看出，高阶振型的阻尼比对顶端突变部位的计算结果影响显著，需要慎重对待。

3 结论

本文以混凝土－钢混合结构为例，对混合结构的阻尼比和突变部位的修正方法进行研究，得出以下结论：

(1)由于不同材料的阻尼特性不同，结构阻尼矩阵不再满足正交性，在构造非经典阻尼矩阵时宜采用4阶振型，以便更好地反映突变部位局部振动振型的耗能特性;

(2)按本文方法构造非经典阻尼矩阵，并按定义式计算得到的振型阻尼比可以较好地反映高阶局部振动振型的耗能特性;

(3)本文基于反应谱理论推导的修正公式具备较高的参考价值，如能在计算程序中准确衡量高阶振型在内力组合时的权重，则所得到的修正系数会更加准确。

［1］中华人民共和国行业标准.高层建筑混凝土结构技术规程(JGJ3－2002)［S］.北京：中国建筑工业出版社，2002.

［2］Newmark N M，Hall W J.Seismic design criteria for nuclear reactor facilities［C］.Proc，Forth World conf.on Earthquake Engrg.，Santiago，Chile，1969.

［3］ Hart G C，Lew M，Dijulio R M.High－rise building response：damping and period nonlinearities［C］.Proc.，Fifth World conf.on Earthquake Engrg.，Rome，Italy，1973.

［4］ Celebi M.Comparison of damping in buildings under lowamplitude and strong motion［J］.Journal of Wind Engineering and Industrial Aerodynamica.1996，59：309 －323.

［5］张辉东，周 颖，元 丰.基于复阻尼理论的流固耦合地震时程响应研究［J］.振动与冲击，2010，29(6)：194 －198.

［6］Chopra A K.著，谢礼立，吕大刚，等译.结构动力学理论及其在地震工程中的应用［M］.北京：高等教育出版社，2007.

［7］王福智.考虑材料阻尼比不同的钢框架－混凝土筒体混合结构弹性时程分析［D］.天津：天津大学，2004.

［8］周向阳，张其林.组合结构等效阻尼比的确定及其在有限元中的应用［J］.计算机辅助工程，2007，16(3)：6－9.

［9］ Huang B C，Leung Y T，Lam K M.Analytical determination of equivalent modal damping ratios of a composite tower in windinduced vibrations［J］.Computers and Structures，1996，59：311－316.

［10］周国伟.考虑不同材料连体结构的抗震、减震若干问题研究［D］.南京：东南大学，2009.

［11］刘大海，杨翠如，编著.高层建筑结构方案优选［M］.北京：中国建筑工业出版社，1996.

［12］高 昂，李爱群，张志强.南京新世纪中心顶部钢塔结构动力特性及地震响应分析［J］.江苏建筑，2005(1)：17－20.

Damping ratio of composite structures used in time-history analysis

ZHOU Guo－wei1，2，ZHANG Zhi－qiang1，3，LI Ai－qun3，XU Jin－jun4

(1.School of Civil Engineering，Southeast University，Nanjing 210096，China;2.Guangzhou Design Institute，Guangzhou 510620，China;3.Southeast University Key Laboratory of Concrete and prestressed Concrete Structures of the Ministry of Education，Nanjing 210096，China;4.Internal Trade Engineering Design and Research Institute，Beijing 100001，China)

There are two main problems in the study of damping effect of composite structures：the first is how to calculate the damping ratio of the whole structure when adopting different materials;the second is how to modify the low damping material after obtaining the integral damping ratio of the whole structure.Taking the high－rise building with steel tower on top as an example，a construction method of non－classical damping matrix was proposed.The result shows the damping ratio based on this matrix can reflect the energy dissipation of 4 orders of modes which play the most important influence on the main structure and the steel tower on top.By the response spectrum method，the inaccuracy of the steel tower's result due to using the calculated integral damping ratio was deduced and a modification equation was provided.The comparison with the accurate result shows the modification factor obtained by the equation has certain reference value to the earthquick response calculation.

composite structure;non－classical damping;damping ratio;high－order vibration mode

O411;O341;TU501

A

既有建筑功能提升改造关键技术(6105001014)

2011－03－02 修改稿收到日期：2011－08－08

周国伟 男，硕士，1984年7月生

张志强 男，博士，副教授，1969年6月生