重复控制在卫星转动部件动量补偿中的应用

王磊，甘克力，葛升民，何平，李爽

(1.哈尔滨工业大学 控制科学与工程系，黑龙江 哈尔滨150001;2.中国空间技术研究院，北京100094)

0 引言

某些卫星的有效载荷具有转动部件，例如光学扫描相机或扫描镜等，这些部件的转动引入了角动量干扰。如果干扰未经补偿直接作用于卫星平台，将会降低姿态控制系统的稳定度和指向精确度[1]。尤其对于具有挠性附件的卫星，如果转动部件的运动为周期性往复运动，则有可能激发挠性附件的振动，使卫星姿态出现振荡。

为减少转动部件对卫星姿态造成的不利影响，引入一个独立的角动量补偿系统，用以直接抵消转动部件的运动影响。选择补偿飞轮作为动量补偿执行部件，为补偿飞轮配置专门控制器，并在有效载荷转动部件上安装角度编码器以测量转动部件的转动角度。控制器根据转动部件的转动角度计算所需要补偿的角动量值，由补偿飞轮输出补偿角动量，保证转动部件与补偿飞轮角动量之和接近于零，这样就可以抵消运动部件的动量干扰。

很多控制系统都要处理周期性参考输入或扰动信号，例如转台伺服系统要以一定的周期重复地操作运行[2]。重复控制基于内模原理将周期信号的动态模型植入系统的控制器内，从而实现对周期性参考输入信号进行高精确度跟踪或对周期性干扰信号进行有效抑制，并且这种机制在跟踪和抑制周期信号方面都取得了一定的成就[3－4]。

在角动量补偿系统工程设计中发现，跟踪转动部件周期运动时传统PID控制器在高频段有一定的相位滞后，并且转动部件在转速过零时存在的摩擦力矩会降低补偿系统的补偿精确度[5]。为保证补偿效果和系统工程实用性，需要采取措施降低这些方面的影响。本文设计方案中选择重复控制方法，在原有PID控制器中插入重复控制环节，不必调整原有控制系统参数即可大幅提高系统精确度。由于引入重复控制器使得补偿系统可以最大限度抵消运动部件的力矩干扰，从而保证卫星实现高姿态稳定度、高指向精确度。本文的主要研究内容有补偿系统方案设计和仿真验证等。

1 补偿系统方案设计

本节简要介绍与角动量补偿系统设计有关的基本信息，包含有效载荷运动特性与摩擦力矩特性等。

1.1 角动量补偿系统

图1为角动量补偿系统示意图，其基座安装于卫星平台之上，转动部件通过转轴和轴承与基座相连做余弦往复式扫描运动，将驱动电机的转子固联于转轴之上，定子与基座相固联。在转轴底部安装角度编码器用于测量转动部件的转动角度位置，为补偿控制器提供测量信号。

利用专门的补偿飞轮在载荷运动的同时做相反方向的转动可以抵消转动部件的角动量干扰。补偿飞轮与有效载荷具有相似的结构，同样具有转动部件(飞轮体)、轴系驱动电机、基座和角度测量装置。驱动电机的转子与飞轮体联接，其定子则安装在外壳基座之上。如图1所示，将补偿飞轮安装于有效载荷基座之内，与有效载荷转动角度测量装置共同构成补偿系统的机械结构部分。

图1 角动量补偿系统Fig.1 Angular momentum compensation system

1.2 有效载荷运动规律

假设有效载荷转动部件的运动规律为余弦扫描运动，其扫描曲线如图2所示。转动部件在5 s内完成12°×24°的对角线扫描，其扫描范围为东/西12°、南/北 24°，扫描机构仅在南北方向运动，单向扫描时间为2.5 s，机械轴转动12°。由图2可知，余弦运动的周期 TL为5 s，将幅值换算为弧度，AL为12° × π/180°=0.209 rad。

图2 转动部件运动规律Fig.2 Motion characteristic of rotating part

假设转动部件南北轴角度位置测量值为θL，角加速度为 αL，则

将相关参数代入式(1)和式(2)可得，最大干扰力矩为

式中，IL为转动部件的转动惯量 2.27 kg·m2，max|·|为对变量取最大值运算。

1.3 摩擦力矩特性

有效载荷转动部件执行机构的摩擦力矩特性如图3所示。图中实线部分所示为实验可以测得的数值，由于转速过零处的摩擦力矩信息难于测量，图中用虚线表示。摩擦力矩在边界润滑和全润滑分界处的最小值约为5 mN·m。由1.2节计算可知，该干扰为转动部件最大干扰力矩的0.6%，转速过零处最大静摩擦力约为20 mN·m。

图3 摩擦力矩特性Fig.3 Characteristic of friction torque

考虑到设计仿真过程中的数值计算问题，摩擦力矩采用 Karnopp摩擦模型[6]，并利用实验数据进行模型参数确定。静摩擦力矩为

式中:Tε表示外加力矩;Ts表示最大静摩擦力矩，此处为20 mN·m，为转动部件转动速度。

表示Stribeck效应的非线性函数为

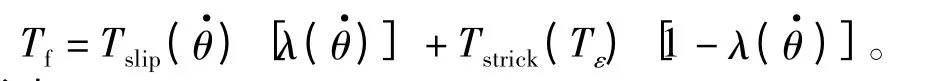
式中，

2 控制器设计

完整的角动量补偿系统由有效载荷、补偿飞轮、PID控制器和重复控制部分构成，其组成框图如图4所示。

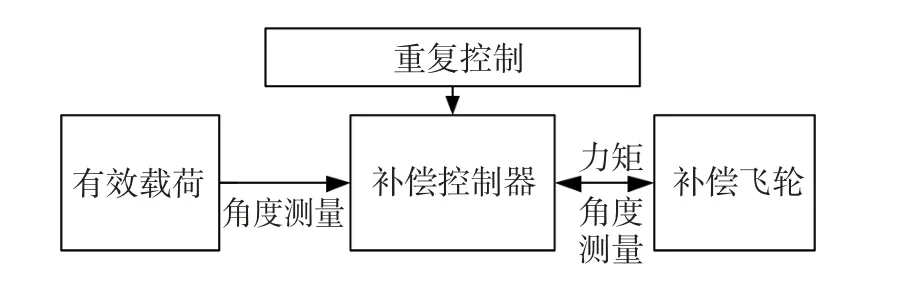
图4 角动量补偿系统Fig.4 Angular momentum compensation system

角动量补偿的最终任务是要使卫星姿态稳定度和指向精确度不受有效载荷转动部件运动的影响，所以角动量补偿的本质是要求同时对转动部件的转动角度和转动角速率进行补偿。实际应用中对于做周期性扫描运动的有效载荷，角动量偏差中应包含两类不同性质的成分:第一类是每个周期内角度位置的最大偏差项，该偏差在每个周期内将重复出现，出现该偏差项的主要原因为控制系统中存在的回滞与失调等因素引起的速率跟踪误差;另一类是角速度偏差的长期累积，该项的大小将随时间的增加而增大，出现该偏差项是由轴承摩擦力矩的不平衡、控制电路中电位指令的不对称性等因素引起的。由于第二类偏差的存在，仅仅跟踪有效载荷的角速率将使残余角动量逐渐累积，最终影响到卫星平台的姿态指向精确度。综上所述按如下方法构造一种双闭环PID控制器，分别引入补偿飞轮的角度位置测量信号和角速度估计信号，角速度为内环控制变量，角度位置为外环控制变量。同时，在外环角度控制器中引入重复控制算法，以有效载荷运动周期为学习周期。角动量补偿系统框图如图5所示，其中有效载荷的干扰力矩由式(2)给出，且包含依据式(1)和Karnopp摩擦模型计算的摩擦力矩信息。

图5 角动量补偿系统框图Fig.5 Block diagram of angular momentum compensation system

图5 中均为变量的z变换形式，其中θL(z)是载荷转动角度位置信号，L(z)是载荷角速度估计，TC(z)是补偿飞轮力矩指令，iC(z)是补偿飞轮的电机电枢电流，TM(z)是补偿飞轮的电机输出力矩，TD(z)是补偿飞轮的摩擦力矩，ωC(z)是补偿飞轮的转速，θC(z)是补偿飞轮的角度位置信号。

图5中的传递函数及其参数均按工程整定法进行设计[7]，具体意义如下:G1(z)是为有限带宽微分，比例系数与微分带宽均选为40 rad/s;G2(z)是具有PID形式的补偿控制传递函数，D项是为了提高闭环响应速度，三项系数分别为0.08、0.7、7，带宽为90 rad/s;G3(z)是补偿飞轮电枢电流闭环传递函数，由电路部分决定;G4(z)是补偿飞轮电机的力矩系数0.25 N·m/A;G5(z)是补偿飞轮控制力矩到角速度传递函数，IC是补偿飞轮转动惯量，为0.006 kg·m2，Ts是系统采样时间0.01 s;G6(z)具有PI形式，主要用于清除补偿飞轮长期角度偏差，比例系数选为1，积分系数为15;Gr(z)为一种插入式重复控制系统。采用这种结构的优点是，原系统控制器和重复控制器的设计相互独立，不必对原有控制器进行任何修改而仅需要增加一个相加环节，重复控制器便可以大幅度地提高系统的稳态精确度，其数学表达式采用最常用的形式，即

式中:N为学习周期;kr＞0用于提高系统响应快速性。

3 仿真计算

仿真用卫星本体的转动惯量为Iy=3 000 kg·m2，在无扰动情况下，卫星平台自身稳定度为2×10－4(°)/s，卫星姿态控制的稳定度要求优于5×10－4(°)/s(3σ)，因此允许的最大补偿剩余力矩对卫星造成的稳定度扰动为3×10－4(°)/s。该卫星的姿态指向精确度要求≤0.03°(3σ)，姿态测量精确度为 3″(3σ)。补偿飞轮转动惯量为0.006 kg·m2，转速为1 000～3 000 r/min。

为了说明加入补偿系统对卫星姿态干扰的补偿效果，本文对加入补偿系统前后卫星的俯仰通道分别进行姿态控制仿真，同时假设卫星没有挠性附件，仿真中卫星俯仰通道采用经典PD控制器，其中比例系数选为66，微分系数选为350。将式(1)中 θL放大倍之后，作为角动量补偿系统输入信号。

图6所示为转动部件以0.2 Hz的频率做扫描运动时对卫星姿态干扰的情况。图中没有加入角动量补偿系统，从图中估算干扰最大值与最小值之差约为3×10－4rad，以1/2周期的变化时间来计算姿态稳定度，有

已经远超过系统的稳定度要求。

图6 无补偿时卫星姿态仿真Fig.6 Attitude simulation with no compensation

图7 所示为加入角动量补偿系统后，转动部件仍以0.2 Hz的频率做扫描运动，此时对卫星姿态干扰的情况。

图7 角动量补偿结果Fig.7 Angular compensation result with compensation

同样以式(3)的方法计算干扰，约为1×10－5(°)/s，达到了系统的补偿要求，抵消掉角动量干扰的99%以上。

图8所示为补偿系统跟踪有效载荷运动的角位置误差。由图7和图8可以看出，重复控制器的引入有效提高了跟踪精确度。初始角度跟踪误差为0.3 rad左右，在仿真时间200 s内已经基本消除了有效载荷对卫星姿态的干扰，补偿系统跟踪误差在400 s内已经收敛，并且具有良好的稳定性。尤其指出，摩擦力矩引入的干扰在引入重复控制器后，已经被抵消掉大部分，从仿真图中很难分辨出来。

实际工程应用中有效载荷驱动机构在速度方向改变处存在较大畸变。重复控制器在抑制该周期性扰动中，也起到关键作用。如果转动部件的扫描频率改变，可以通过有效载荷控制器在轨运行时改变学习周期参数，向补偿系统发送一个频率改变信号即可。甚至当运动为未知随机运动时，可以关闭重复控制器，仅保留PID控制器工作。此外要说明的是，重复控制器中的kr不能选取过大，否则会使补偿系统发散，本文中kr选为20。

图8 补偿系统的跟踪误差Fig.8 Tracking error of compensation system

4 结论

本文通过一种基于插入式重复控制与经典PID控制相结合的角动量补偿系统，抑制了卫星有效载荷运动所带来的角动量干扰。仿真结果表明，相对于经典PID控制器，插入重复控制方法降低了周期跟踪信号的跟踪误差，加快了收敛速度，同时对周期干扰的抑制也起到了关键作用，而且独立于原有控制器的设计方法，降低了插入重复控制对原系统的影响，同时增加了系统的灵活性。

[1]CHEN Maoliang，LIU Yingying，LEI Jing，et al.On-orbit identification of disturbance torques acting on satellite with rotating payloads[C]//Proceedings of the 2009 IEEE International Conference on Mechatronics and Automation，August 9 － 12，2009，Changchun，China.2009:1342－1346.

[2]杨松，曾鸣，苏宝库.重复控制算法在转台伺服系统中的应用[J].电机与控制学报，2007，11(5):508－511.YANG Song，ZENG Ming，SU Baoku.Repetitive control algorithm in turntable servo system[J].Electric Machines and Control，2007，11(5):508 －511.

[3]Tomizuka M.Dealing with periodic disturbances in controls of mechanical systems[J].Annual Reviews in Control，2008，32:193－199.

[4]YUAN Songgui，WU Min，HE Yong，et al.Non-fragile discrete repetitive control based on two-dimension model[C]//Proceedings of the 29th Chinese Control Conference，July 29－31，2010，Beijing，China.2010:243 －247.

[5]CHEN Silu，TAN Kok Kiong，HUANG Sunan.Friction modeling and compensation of servomechanical systems with dual-relay feedback approach[J].IEEE Transactions on Control Systems Technology，2009，17(6):1295－1305.

[6]Karnopp D.Computer simulation of slip-stick friction in mechanical dynamic systems[J].Journal of Dynamic Systems，Measurement，and Control，1985，107(1):100 －103.

[7]Goodwin G C，Graebe S F，Salgado M E.Control System Design[M].New Jersey:Prentice-Hall，2001.