一种基于支持向量机的矢量控制方法及应用

王德成， 林辉

(西北工业大学自动化学院，陕西西安710072)

0 引言

永磁同步电机(permanent magnet synchronous motor，PMSM)采用永久磁铁产生气隙磁通而不需要外部励磁，具有极好效率特性、极高的功率密度以及转矩/惯量比等优点，成为伺服控制系统驱动电机的首选［1］。矢量控制以转子磁链矢量为参考坐标，将定子电流分为励磁分量和转矩分量分别进行独立控制，不论在电机低速运行区还是在电机高速运行区具有较好的抗扰动性能、启动制动性能和稳定性能，是永磁同步电机的主要驱动控制策略［2］。

矢量控制需要借助于三角函数计算进行坐标变换，但由于微控制器尚不具备直接进行三角函数计算的能力，限制了矢量控制在微控制器中应用的灵活性。目前普遍采用查表法来实现三角函数的计算［3］。表的容量太大，需要大的存储空间;表的容量太小会产生较大的电流谐波畸变和脉动转矩。文献［4－9］提出采用神经网络实现三角函数运算。神经网络的高精度学习是建立在大量训练样本基础之上，具有较多的权重因子，在线计算三角函数时需要大量的运算，限制功率器件的开关频率。而且，为了实现高精度的三角函数计算，传递函数中含有指数项，不适合直接在微控制器中应用。

支持向量机(support vector machine，SVM)是一种基于结构风险最小原理的机器学习方法［10］。它通过非线性映射将输入向量映射到高维特征空间中，然后在此构建最优分类面。该分类面不仅能够尽可能多的将两类数据点正确的分开，同时使分开的两类数据点距离分类面最远。SVM在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势，在参数辨识领域得到很好的应用［11－12］。

针对永磁同步电机矢量控制中三角函数计算问题，本文提出一种新的永磁同步电机矢量控制方法，以多项式核SVM离线训练三角函数得到的权向量和阈值为基础，通过易于微控制器实现的加法、减法和乘法实现矢量控制坐标变换所需的三角函数运算，增加了矢量控制在微控制器中应用的灵活性。将该方法应用于永磁同步电机调速系统中，结果表明该方法的可行性和有效性。

1 永磁同步电机矢量控制

永磁同步电机矢量控制采用固定于转子的两相旋转坐标系(dq轴系)来描述和分析。取永磁体基波励磁磁场轴线(磁极轴线)为直轴d，而交轴q顺着旋转方向超前d轴90°电角度。dq轴系随同转子以电角频率ωr一起旋转，它的空间坐标以d轴与A相绕组轴线间的电角度θr来确定。三相静止坐标系 ABC 下的 ia、ib、ic与 dq 轴系下 id、iq关系为

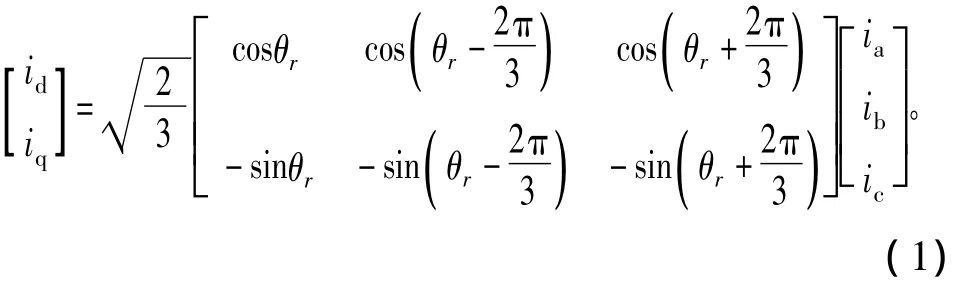
在忽略铁心饱和、涡流和磁滞损耗、转子上的阻尼绕组，以及假设永磁材料的电导率为零的前提下，dq轴系下PMSM的数学模型为

式中:p为微分算子;Rs是相绕组电阻;Ld和Lq分别是d、q轴线圈的自感;Lsδ是d、q轴线圈的漏感;Lmq、Lmd是d、q轴的励磁电感;if为等效励磁电流。

电机的转矩为式中pn为极对数。

式(3)中第一项是主电磁转矩，第二项是由转子凸极效应引起的磁阻转矩。通过控制id、iq实现转矩的控制。将控制器输出的控制指令id、iq，转换成 iα、iβ，即

根据iα和iβ，利用SVPWM方法输出6脉冲逆变器驱动控制信号，实现PMSM变频调速控制，结构原理图如图1所示。

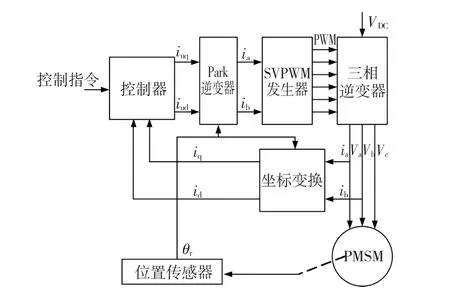
图1 PMSM矢量控制结构原理图Fig.1 PMSM vector control structure diagram

2 一种新的矢量控制方法

2.1 支持向量机

yj∈R 给定训练数据{(xj，yj)，j=1，2，…，k}，xj∈Rn，为第j个学习样本的输入值，为对应的目标值，通过一个非线性映射Φ将输入样本空间映射到一个高维特征空间，然后在高维特征空间构造线性回归函数，即

采用ε不敏感损失函数，根据结构风险最小化原则，要解决的原始最优化问题形式为

式中(*)表示向量有*号和无*号两种情况的简单记号。

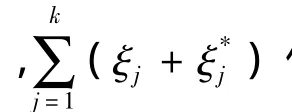
选择合适的核函数K，求解该对偶问题得到最优解α(*)，并根据KKT条件计算得到b，构造非线性回归函数，即

2.2 基于SVM的矢量控制

利用SVM对正弦函数进行训练，可得到正弦函数的逼近表达式为

由式(9)可知，采用多项式核函数进行训练，可将正弦函数运算转换成加法、减法和乘法。令

则sinβ=cosθ。因此只通过对正弦函数进行训练，就可以完成矢量变换所需的三角函数运算。ia、ib、ic的矢量和为零，ia、ib、ic与 id、iq关系可表示为

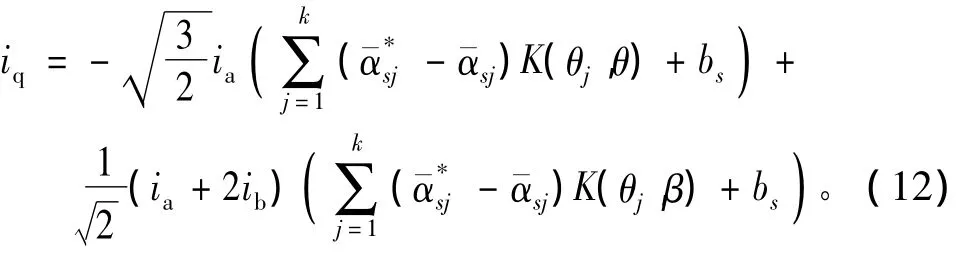
id、iq与 iα、iβ的关系可表示为

利用SVM训练正弦函数得到的权向量和阈值逼近三角函数，可以实现矢量变换中的坐标变换。式(11)～式(14)中只含有加法、减法和乘法，可以方便的在微控制器中实现矢量控制。

3 实验分析

实验选用的微控制器为TMS320F2812 DSP芯片，时钟频率为150 MHz。采用的永磁同步电机极对数为2，额定电流2.1 A，额定电压27 V。编码器采用霍尔磁电编码器作为位置检测元件。电流采样采用霍尔电流传感器ACS712。功率开关管采用MOSFET IRFR3910。控制策略采用id=0的矢量控制。实验装置如图2所示。其中力矩传感器采用V型智能转矩转速测量仪，转矩显示采用JN338M－F型扭矩测量仪，负载采用FZ10型磁粉制动器。线性可调直流电源用于控制磁粉制动器。实验过程中，通过调节线性可调直流电源控制负载力矩的大小。

图2 实验装置Fig.2 Experiment device

以角度为输入变量和角度对应的正弦值为输出变量，对0～360°范围的角度值均匀采样20点，构成包含20个数据的训练集。采用多项式核函数，对训练集进行离线训练。训练得到的权向量和阈值输入到DSP中作为进行三角函数计算的参数。为了验证所提方法的有效性，实验还采用了基于1 000点查表方法的矢量控制方法(Lookup－VC)。

图3为本文所提方法(SVM－VC)，在恒压频比控制模式下，转速为600 r/min时A相电流波形。图4为恒压频比控制模式下，转速为600 r/min时电流谐波畸变率随谐波次数的变化。图5为闭环转速600 r/min控制时，SVM－VC在不同负载下转速波动。图6为本文所提方法SVM－VC和Lookup－VC在转速分别为 200 r/min、400 r/min、600 r/min、800 r/min、1 000 r/min闭环控制时且在0.2 N·m负载下的转速波动。

图3 A相电流波形Fig.3 Phase A current waveform

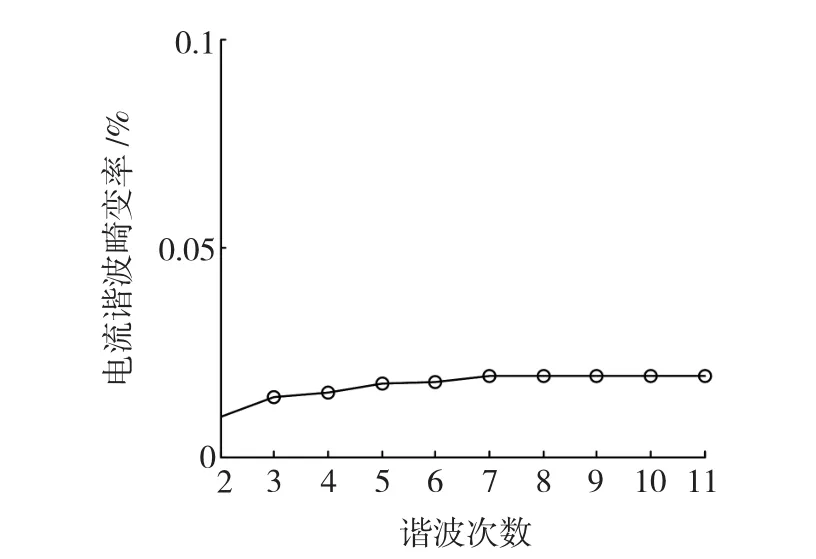
图4 电流谐波畸变率随谐波次数的变化Fig.4 The change of current harmonic distortion with harmonic number

图5 不同负载下闭环控制转速波动Fig.5 Close loop control speed fluctuating with different loads

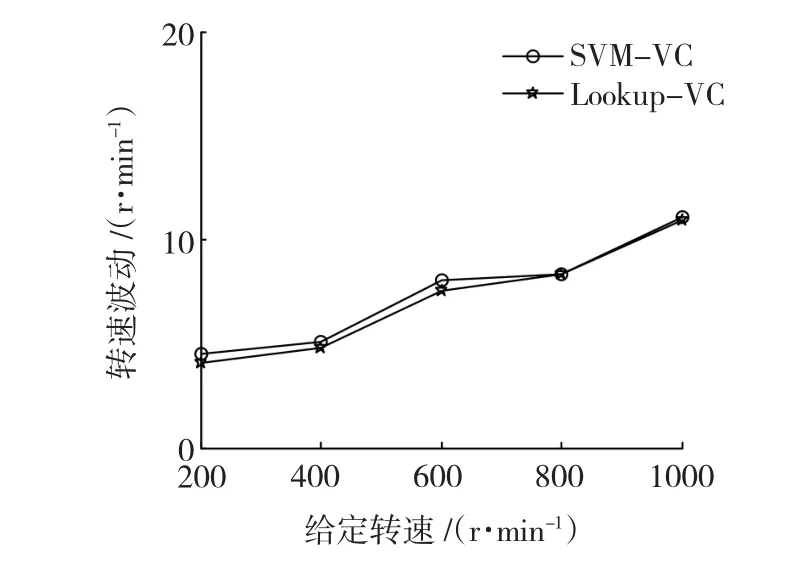
图6 不同转速下的闭环转速波动Fig.6 Close loop control speed fluctuating with different speeds

图3中，恒压频比控制模式下A相电流波形比较贴近正弦波。图4中，A相电流总谐波畸变率较小，其中前11次电流谐波畸变率仅为1.94%。这说明控制方法中采用基于SVM的三角函数运算具有较高的计算精度。图5中，不同负载下，闭环控制转速波动小于9 r/min，控制精度优于99%，具有较好的转速控制性能。图6中，不同转速闭环控制下拖动相同负载时，SVM－VC和Lookup－VC具有相似的转速波动，在控制性能方面相似，但是SVMVC需要较少的存储空间。

4 结语

以多项式核SVM对正弦函数进行训练得到的参数，通过加法、减法和乘法实现矢量控制所需三角函数的逼近，增加了矢量控制在微控制器中应用灵活性。利用该方法实现基于微控制器的永磁同步电机调速控制，结果表明该方法具有较好的调速性能。

［1］ 王成元，夏加宽，孙宜标.现代电机控制技术［M］.北京:机械工业出版社，2009:104－130.

［2］ 鲁文其，胡育文，杜栩杨，等.永磁同步电机新型滑模观测器无传感器矢量控制调速系统［J］.中国电机工程学报，2010，30(33):78－83.

LU Wenqi，HU Yuwen，DU Xuyang，et al.Sensorless vector control using a novel sliding mode observer for PMSM speed control system［J］.Proceedings of the CSEE，2010，30(33):78 －83.

［3］ PINTO J O P，BOSE B K，DA SILVA L E B，et al.A neural-network-based space-vector PWM controller for voltage-fed inverter induction motor drive［J］.IEEE Transactions on Industry Applications，2000，36(6):1628 －1636.

［4］ MONDAL S K，PINTO J O P，BOSE B K.A neural-networkbased space-vector PWM controller for a three-level voltage-fed inverter induction motor drive［J］.IEEE Transactions on Industry Applications，2002，38(3):660 －669.

［5］ WANG Cong，BOSE B K，OLESCHUK V，et al.Neural-network-based space-vector PWM of a three-level inverter covering overmodulation region and performance evaluation on induction motor drive［C］//The 29th Annual Conference of the IEEE Industrial E-lectronics Society，November 2 － 6，2003，Roanoke，United States.2003:1 －6.

［6］ MUTHURAMALINGAM A，SIVARANJANI D，HIMAVATHI S.Space vector modulation of a voltage fed inverter using artificial neural networks［C］//International Conference of 2005 IEEE India Council，December 11 －13，2005，Chennai，India.2005:487－491.

［7］ DZUNG P Q，PHUONG L M，NHO N V，et al.The development of artificial neural network space vector PWM and diagnostic controller for voltage source inverter［C］//2006 IEEE Power India Conference，April 10 －12，2006，New Delhi，India.2006:521－528.

［8］ 蔡宝平，刘永红，张海峰.基于人工神经网络的SVPWM技术［J］.电力系统及其自动化学报，2010，22(1):44 －48.

CAI Baoping，LIU Yonghong，ZHANG Haifeng.Space vector PWM based on wavelet neural network［J］.Proceedings of the Chinese Society of Universities for Electric Power System and its Automation，2010，22(1):44 －48.

［9］ 潘庭龙，纪志成，谢林柏，等.基于ANN的一种新型SVPWM控制器设计［J］.系统仿真学报，2006，18(2):420 －423.

PAN Tinglong，JI Zhicheng，XIE Linbo，et al.Design of novel ANN － based SVPWM controller［J］.Journal of System Simulation，2006，18(2):420 －423.

［10］ VAPNIK V N.The nature of statistical learning theory［M］.New York:Springer，1995.123 －170.

［11］ 宋建成，郑建斌，曲兵妮，等.开关磁阻电机的最小二乘支持向量机建模与仿真［J］.电机与控制学报，2010，14(5):44－48.

SONG Jiancheng，ZHENG Jianbin，QU Bingni，et al.Modeling and simulation for switched reluctance motor based on least squares support vector machine［J］.Electric Machines and Control，2010，14(5):44 －48.

［12］ 陈杰，朱琳.基于混合最小二乘支持向量机网络模型的非线性系统辨识［J］.控制理论与应用，2010，27(3):303－309.

CHEN Jie，ZHU Lin.New identification approach for nonlinear systems based on the combination network model of least squares and support vector machines［J］.Control Theory ＆ Applications，2010，27(3):303 －309.