正交磁化可控电抗器的设计与特性分析
朱宝森, 关毅, 陈庆国, 池明赫, 魏新劳
(哈尔滨理工大学电气与电子工程学院,黑龙江哈尔滨150080)
0 引言
随着电力工业的发展,可控电抗器广泛应用于电网无功补偿、限制过电压以及改善电能质量等方面。目前,传统机械式可控电抗器无法实现连续平滑可调;晶闸管控制可控电抗器控制灵活,但因其不可避免的谐波问题使其在高压电网中应用受到限制;磁阀式可控电抗器控制灵活、成本低[1],广泛应用于大容量无功补偿,但因饱和电抗器设计工作在极限饱和区,故负载能力差,不利于过电压的限制。因此高压大容量、电感值连续可调、谐波含量低是可控电抗器的发展趋势。正交磁化可控电抗器是一种起步较晚的直流磁控式电抗器,它是由参数变压器发展而来。1965年美国Wanlass公司申请专利,提出由参数器件组成的可变电感器及其组成的稳压器[2]。1967年该公司首次公开介绍参数变压器这一概念,其磁路由一对C型铁心正交对接;1968年又在Wescon发表论文,全面叙述了参数变压器的工作原理[3]。1972年,加拿大W.Z.Fam 等人在文献[4]中用数学方法论证了参数变压器运行特性。1974年,Z.H.Meiksi对参数变压器的电气性能进行研究,它具有抗干扰、稳压、过载保护、不会过压、线性度好等许多优良特性。此后出现多种形式的参数变压器,其中包括不同磁路结构和绕组安排形式。Z.H.Meiksin在文献[5]中对正交和平行磁通进行分析对比发现:正交磁通电抗器具有良好的线性特性,平行磁通电抗器具有较大的调节范围。日本学者针对正交铁心结构提出了三维磁阻网络法建立磁通模型[6],三维磁阻网络法的提出对于正交磁通装置计算具有重要意义[7]。日本学者Osamu Ichinokura提出了一种应用于VAR补偿装置中正交铁心可调电抗器[8-9],学者们针对电抗器磁路非线性引起的谐波问题进行了大量研究[10-12]。文献[13]中提出一种圆筒结构的正交磁化可控电抗器应用于高压直流输电装置的交流调谐滤波器中。
本文详细介绍了一种链式正交磁化可控电抗器的结构和磁化机理,建立了其磁路模型和数学模型。通过理论计算与仿真研究,设计与制作了电抗器的实物模型,并对其参数及性能进行试验验证。
1 可控电抗器结构和磁化机理
1.1 正交磁化可控电抗器的结构
正交磁化可控电抗器采用两个矩形铁心在空间上正交的链式结构,工作绕组WI和控制绕组WII分别固定在铁心I、铁心II上,其结构如图1所示。当控制绕组中无直流电流时,铁心I中只有交流磁通Φa,在绕组WII中施加直流控制电流id后在铁心II中产生直流磁通Φd,Φa与Φd在两铁心的公共部分相互正交产生正交磁场。调节idc来改变两铁心公共部分的磁场强度,由于铁磁材料的非线性,电抗器的电感量随着控制电流增加而减小。

图1 正交磁化可控电抗器结构Fig.1 Structure of controllable reactor based on orthogonal magnetization
1.2 磁化机理
调节正交磁化可控电抗器的关键在于调节正交磁场下铁磁材料磁导率。铁磁材料在稳恒磁场和交变磁场同时作用的情况下,铁磁材料的磁导率具有张量形式的性质[14]。其交变的磁感应强度和交变磁场强度一般关系为:[b]=[h],其中为张量磁导率,b为磁场感应强度,h为磁场强度。

当磁场只有x轴分量hx时,hz=hy=0。则有

由此可知,当铁磁材料的磁导率为张量时,某一坐标轴的磁场不仅产生该坐标轴上的磁感应强度,同时也产生其他坐标轴的磁场强度。故外加直流磁场作用不仅改变直流磁场方向的磁导率,也改变交流磁场方向磁导率[15]。
铁磁材料的磁导率主要取决于磁畴壁移和转向的难易程度[16]。当正交磁化电抗器的铁心仅受到交流磁场作用时,铁磁材料的磁畴会转向交流磁场的方向,施加与交流磁场正交的直流磁场后,直流磁场抑制磁畴向交流磁场方向发展,部分磁畴会由交流磁场方向向直流磁场方向偏转,直流磁场越强其偏转幅度越大。进而降低了沿交流磁场方向的磁导率,达到了控制电感量的目的。图2为正交磁化电抗器铁心公共部分的磁场分布。
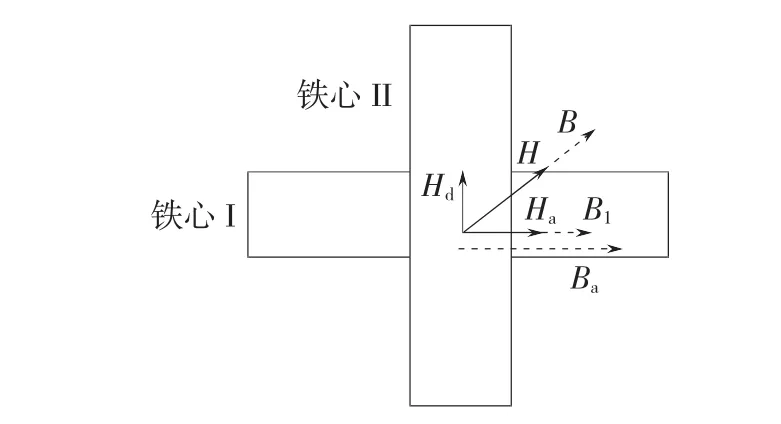
图2 电抗器铁心公共部分磁场分布Fig.2 Magnetic field distribution of public portion of the reactor core
图2中,Ba为无直流磁场强度时Ha2所产生的交流磁感应强度。施加直流磁场强度Hd2,此时公共部分磁场强度H=Ha2ex+Ha2ey,exey为坐标轴单位向量。由H产生的磁感应强度B可分解为x轴分量B1、y轴分量B2。由于磁化曲线非线性,Ba减小为B1。故在施加直流磁场后,交流方向磁导率减小,可等效为电感值的减小。正交磁化可控电抗器与传统饱和电抗器不同,传统饱和可控电抗器工作在饱和区,由于材料的非线性容易引起谐波产生。正交磁化可控电抗器铁心在正交磁场的作用下,通过调节直流磁场使铁心工作在不同直流磁场强度下的磁化曲线上,从而改变了铁磁材料的磁导率。若能控制铁心工作在每条磁化曲线的线性区,则可以避免因材料饱和而引起的非线性谐波产生。
2 等效磁路及数学模型
2.1 等效磁路
由图1所给出正交磁化可控电抗器铁心中的磁通分布,根据电磁场理论正交磁化可控电抗器工作侧磁路可等效为图3所示的磁路模型。工作侧铁心磁阻可分为两部分,非公共部分磁阻Ra1,公共部分磁阻Ra2。通过调节Ra2可实现对电抗器的调节。

图3 铁心等效磁路Fig.3 Equivalent magnetic circuit of core
2.2 数学模型
根据基本电磁场理论可得到电磁方程为

根据全电流定律有
交流铁心平均磁路长度la=la1+la2,直流铁心平均磁路长度ld=ld1+ld2。其中,la1、la2分别为交流铁心非公共部分以及公共部分磁路长度;ld1、ld2分别为直流控制铁心的非公共部分以及公共部分磁路长度;Bac、Bdc分别为两铁心中的磁通密度;Ha1、Hd1分别为交直流铁心中非公共部分的交流磁场方向及直流磁场方向的磁场强度;Aac、Adc分别为交流铁心及直流铁心截面积;Bac、Bdc分别为交流铁心及直流铁心中的磁通密度;Nac、Ndc分别为工作绕组及控制绕组匝数;iac、idc分别为交流工作电流及直流控制电流。
根据图2所描述的磁场分布,由H=f(B)可以得到正交磁场下Ha2、Hd2的表达式为
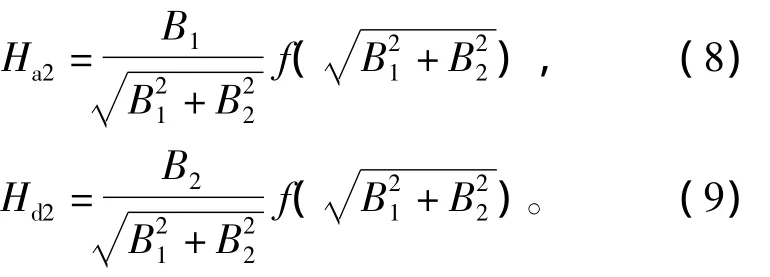
其中,交流铁心磁通Φa=B1Aac,直流铁心磁通Φd=B2Adc,B1、B2分别为交流铁心及直流铁心的磁通密度。
铁磁材料非线性磁化曲线可描述为

式中:a、b为铁磁材料的特性参数。
将式(8)、式(9)、式(10)代入式(6)、式(7)整理得到正交磁化可控电抗器的数学模型为
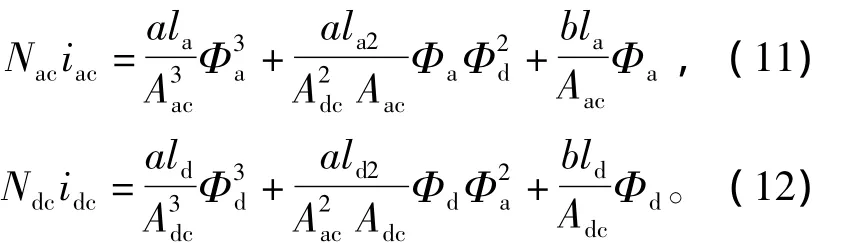
根据上述数学模型可以得到Φa、Φd与iac、idc的关系,在给定任意材料以及尺寸的条件下,由L=NacΦa/iac可计算出直流控制电流与电抗器的电感值的关系。

工作侧施加交流激励U=Umcosωt,则工作侧磁通可表示为 Φa= Φmsinωt,Φm=Um/ωNac,Um为交流电源幅值。由式(12)工作侧绕组电流iac可表示为

由式(14)可知,工作电流iac随控制侧磁通Φd的增加而增加,等效为电抗器的电感值减小。在工作绕组电流中含有 3次谐波,由 sin3ωt、sinωt的系数可以得到3次谐波含量占基波含量的比例。

由式(15)可知,Φd越大3次谐波含量越少。
3 模型设计及有限元分析
3.1 模型设计
根据上述数学模型所描述的电抗器内部及外部参数关系,可进行正交磁化电抗器的参数设计。电抗器的设计分为工作侧铁心及绕组设计和控制侧铁心及绕组设计两部分进行。容量计算公式为

式中:S为电抗器的容量;UN为额定工作电压;L为电抗器的电感值;ω为电源角频率。
根据上述交流等效磁路得到电感计算公式为

式中:Nac为工作绕组匝数;μ1为交流铁心磁导率;μ2为铁心公共部分磁导率。
根据SN由式(18)可初步设计交流铁心截面积Aac,确定交流铁心截面边长c1、c2。B为额定工作状态下交流铁心磁通密度。由式(19)可初步确定工作绕组匝数Nac。根据铁心尺寸和工作绕组尺寸可得到 la。

Aac、Nac、la已确定,选定铁心材料,可确定交流铁心磁导率μ1及直流铁心磁导率 μ2max。根据式(9)、式(10)中所描述的正交磁通关系可以得到

电抗器无控制电流时,公共部分磁导率为μ2max电抗器有最大电感值Lmax,此时容量为最小值Smin;控制电流增加至直流铁心饱和,公共部分磁导率为μ2min电抗器有最小电感值 Lmin,此时有最大容量Smax(SN)。两种状态下的计算方程可表示为

由式(17)可知,la2尺寸决定了Smin可否达到设计要求。根据式(22)可计算得到la2,代入式(21)中可计算得到Smin。以上完成交流铁心部分的设计。
直流侧铁心及控制绕组的设计。由于两铁心正交,直流铁心尺寸可根据交流铁心及交流绕组尺寸来确定。根据安培环路定律由式(7)可确定直流绕组匝数Ndc及直流控制电流Idc。Idc为最大值时,交流铁心达到饱和状态,此时磁通密度B2=1.8 T。确定控制电流Idc时需考虑以下因素:①控制电流过大会增加损耗影响性能;②绕组匝数太多会增加不必要成本。因此设计控制电流时既要保证可行性又要考虑经济性。确定以上直流部分参数设计后,采用能量法计算电感进行验证校核,调整后完成电抗器的整体设计。
3.2 实际算例
为验证正交磁化可控电抗器的设计方法以及测试其电气性能,设计制作了一台6 kVA/220 V的电抗器实体模型,其设计参数如表1所示。

表1 电抗器理论设计参数Table 1 Theory design parameters of the reactor
上表中,Lmax、Lmin为电抗器的最大和最小电感值,Idcmin为公共铁心饱和时控制绕组所需的最小电流值,Iacmax为最小电感值下工作绕组的额定电流值。铁心选用0.5 mm厚取向硅钢片,所设计的电抗器模型尺寸如表2所示。

表2 可控电抗器模型尺寸Table 2 Dimensions of the controlled reactor model
3.3 有限元仿真及结果分析
通过有限元方法将求解区域分割成细小子区域,采用适当尝试函数对电抗器进行电磁问题求解。按照算例模型的实际尺寸建立Ansoft三维有限元模型,图4为电抗器的有限元网格划分模型。

图4 电抗器铁心的有限元模型Fig.4 Finite element model of the reactor core
通过静态磁场求解可以得到,idc=0 A时的电感值Lmax=122.5 mH,与最大电感理论计算值较接近,并可直观的描绘出铁心中磁通分布情况。
在正交磁化可控电抗器的仿真模型中,通过改变控制侧和工作侧的激励源大小来观察磁通密度大小以及方向的变化。将求解问题分别在单一磁场作用下(控制侧电流idc=0 A)以及正交磁场作用下(控制侧电流idc=35 A)两种状态进行仿真。在图4中铁心的正交处切割出一个与XZ平面平行的截面,可观察截面上两铁心正交处磁通分布情况,如图5、图6、图7所示。
单一磁场状态下,铁心在交流磁场作用下的磁矢量分布情况如图5所示。交流铁心上的磁通密度沿交流铁心环绕方向分布,由于直流铁心存在,使得交流磁通在铁心公共部分处产生磁通扩散的现象。
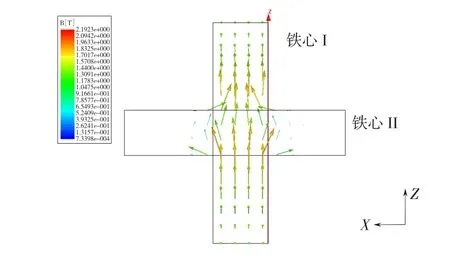
图5 交流磁场下磁通密度矢量分布Fig.5 Magnetic density vector distribution under AC magnetic field
正交磁场下,铁心公共部分磁矢量分布如图6所示。由于直流磁场的存在,使得铁心公共部分的磁矢量方向发生偏转,直流磁场强度越强偏离交流磁场方向的角度越大。

图6 正交磁场下磁通密度矢量分布Fig.6 Magnetic density vector distribution under orthogonal magnetic field
图7为正交磁场下铁心公共部分的磁通密度分布云图。在两铁心正交处有磁场叠加磁场强度较高,磁感应强度B=1.9~2.0 T,通过调节公共部分的磁场强度可达到调节电抗器电感量的目的。

图7 正交磁场下磁通密度分布Fig.7 Magnetic density distribution under orthogonal magnetic field
4 实验研究及结果分析
4.1 模型电抗器基本参数测量
为验证3.1中设计方法的正确性,将设计与制作的模型电抗器依照图8的实验电路搭建实验平台进行物理参数测量。

图8 可控电抗器实验原理接线图Fig.8 Test circuit diagram for controlled reactor
测量结果如表3所示,工作侧绕组施加交流电压激励,控制侧的直流电流分别在idc=0 A及idc=35 A状态下,测量交流工作侧电压及电流值。根据公式L=U/ωI计算可得到Lmax、Lmin。电抗器可调范围计算公式TL=(Lmax-Lmin)/Lmax。当电抗器达到最小电感值时,测得电抗器交流工作电流为22.4 A。电抗器理论设计计算值为27 A,计算得到工作电流的误差率为17%。

表3 电抗器实测参数Table 3 Test parameters of the reactor
实验结果与理论计算结果相比较,二者符合较好,可证明电抗器的设计方法具有合理性。理论计算值与实验测量值存在一定偏差,分析产生误差原因有以下几点:1)铁磁材料磁化曲线数据与实际铁心材料存在一定偏差;2)计算电感时忽略铁心正交处的边缘效应;3)加工精确度引起的误差。
4.2 电抗器的控制特性
根据正交磁化可控电抗器原理可知,随直流控制电流增大电感量减小。为验证这一控制关系,改变模型电抗器控制绕组中的直流电流,测得交流绕组的交流电压、电流值,并根据公式L=U/ωI计算出电感值,绘得的L=f(idc)曲线如图9所示。

图9 电抗器控制特性Fig.9 Control characteristics of the reactor
实验结果显示,正交磁化可控可实现连续平滑调节。随直流增大电抗器有效电感量明显减小,其控制特性曲线为非线性曲线,随控制电流继续增大,直流侧铁心接近饱和,电感量变化幅度变小。
4.3 电抗器的伏安特性
理论分析表明,电抗器在额定工作电压范围内,其伏安特性与工作电压无关,只与控制电流有关。为验证这一理论,对控制绕组施加分别施加0 A、5 A、10 A和20 A控制电流情况下,改变电抗器工作绕组的交流工作电压,测得的不同工作电压下的伏安特性曲线如图10所示。
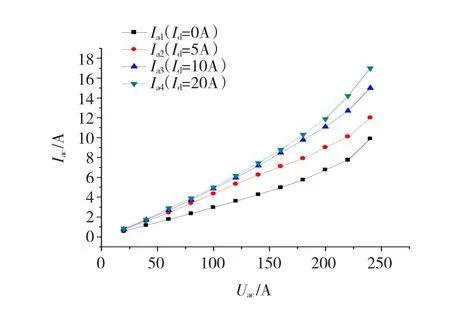
图10 电抗器伏安特性曲线Fig.10 V-A characteristics curves of the reactor
实验结果显示,在额定工作电压范围内曲线近似为线性,当工作电压超出额定工作电压时,伏安特性曲线为非线性,斜率增加,表明此时交流铁心达到饱和。
4.4 电抗器的谐波特性
正交磁化可控电抗器由于绕组及铁心的正交结构,使其具有良好的谐波特性。通过实验可验证这一理论,在交流绕组上施加一个正弦电压信号,实验采用电流互感器采集工作侧绕组上的电流信号,通过傅里叶变换对工作测电流进行计算,测得在不同直流控制电流下电抗器交流绕组基波及各次谐波电流的幅值。
总的谐波畸变率(total harmonic distortion,THD)的计算公式为

根据实际测量值及式(23)得到的不同控制电流下的谐波畸变率如表4所示。

表4 不同控制电流下的谐波畸变率Table 4 THD under different control current
由表4可知,设计的正交电抗器其最大谐波畸变率为4.5%。文献[17]中给出了传统饱和可控电抗器的总谐波畸变率为41.9%。通过比较可知,与传统饱和电抗器相比正交磁化可控电抗器的谐波含量很低,直流控制电流对电抗器的电流频谱影响小。
5 结论
本文分析了正交磁化原理,建立电抗器交流等效磁路并推导出正交磁化可控电控电抗器的数学模型,对正交电抗器进行理论参数设计。采用有限元法进行分析计算。通过实验方法验证设计方案的合理性,并测试其电气性能。实验结果表明:1)本文中电抗器模型的设计方案合理;2)正交磁化电抗器具有非线性控制特性,通过调节控制绕组中的电流,可实现电感量的连续平滑调节,且由于铁心闭合,控制电流小;3)由于控制绕组与工作绕组正交,彼此互不干扰,故电抗器具有较好的线性特性,谐波含量低;4)在额定工作电压范围内,电抗器为线性伏安特性。
[1] 田铭兴,励庆孚,王曙鸿.磁饱和式可控电抗器的等效物理模型及其数学模型[J].电工技术学报,2002,17(4):18 -21,35.
TIAN Mingxing,LI Qingfu,WANG Shuhong.An equivalent physical model and a mathematical model of the controlled saturable reactor[J].Transactions of China Electro Technical Society,2002,17(4):18-21,35.
[2] BURIAN K.Theory and analysis of a parametrically excited passive power converter[J].IEEE Transactions on Industry Application,1975,8(5):278 -282.
[3] 赵伟.正交磁通参数振荡装置的研究与应用[J].电工技术杂志,1994(2):2-8.
[4] FAM W Z,VERMA R P.Theory and performance of parametric transformers[J].IEEE Transactions on Power Apparatus and Systems,1972,91(6):2494 -2504.
[5] Z.H.Meiksin.Comparison of orthogonal and parallel-flux variable inductors[J].IEEE Transactions on Industry Application,1974,10(3):417-423.
[6] TAJIMA K,KAGA A,ANAZAWA Y,et al.One method for calculating flux-MMF relationship of orthogonal-core[J].IEEE Transactions on Magnetics,1993,29(6):3219 -3227.
[7] NAKAMURA Kenji,YOSHIDA Hirokazu,ICHINOKURA Osamu.Electromagnetic and thermal coupled analysis of ferrite orthogonal-core based on three-dimensional reluctance and thermalresistance network model[J].IEEE Transactions on Magnetics,2004,4(7):2050-2052.
[8] ICHINOKURA Osamu,JINZENJI Toshimasa,K Tajima.New variable inductor for VAR compensation[J].IEEE Transactions on Magnetics,1993,29(6):3225 -3227.
[9] NAKAMURA Kenji,ICHINOKURA Osamu,MAEDA Mitsuru,et al.Analysis of orthogonal-core type linear variable inductor and application to VAR compensator[J].IEEE Transactions on Magnetics,2000,5(9):3565 -3567.
[10] 牟宪民,王建赜,魏晓霞,等.新型正交铁心可控电抗器[J].中国电机工程学报.2008,28(21):57-62.
MU Xianmin,WANG Jianze,WEI Xiaoxia,et al.Novel ferrite orthogonal core controllable reactor[J].Proceedings of the CSEE,2008,28(21):57-62.
[11] 魏晓霞,刘杰,纪延超,等.基于谐波反向补偿原理的新型正交可控消弧线圈[J].中国电机工程学报,2007,27(18):90-95.
WEI Xiaoxia,LIU Jie,JI Yanchao,et al.A novel orthogonal controllable exitinction coil based on inverse harmonic compensation theory[J].Proceedings of the CSEE,2007,27(18):90-95.
[12] 牟宪民,刘凤春,王建赜,等.EU正交铁心可控电抗器[J].中国电机工程学报,2009,29(24):122-126.
MU Xianmin,LIU Fengchun,WANG Jianze,et al.EU ferrite orthogonal core variable inductor[J].Proceedings of the CSEE,2009,29(24):122-126.
[13] LESCALE V F.Modern HWC:State of the art and development trends[C]//IEEE International Conference on Power System Technology,August 18 - 21,1998,Beijing,China.1998:446-450.
[14] 廖绍彬.铁磁学[M].北京:科学出版社,1988:102-106.
[15] 蒋正荣,邹军,陈建业,等.基于直流激磁半铁心可调电抗器[J].电力系统自动化,2007,31(5):76-79.
JIANG Zhengrong,ZOU Jun,CHEN Jianye,et al.Semi-core variable inductor based on DC excitation field[J].Automation of Electric Power Systems,2007,31(5):76-79.
[16] 同向前,薛钧义.电子式连续可调电抗器的控制特性[J].电力自动化设备,2005,25(1):25-27.
TONG Xiangqian,XUE Junyi.Control characteristics of electronic continuously tunable reactor[J].Electric Power Automation E-quipment,2005,25(1):25 -27.
[17] 牟宪民,王建赜,胡泰,等.新型单相低谐波饱和式可控电抗器[J].电力自动化设备,2007,27(7):17-21.
MU Xianmin,WANG Jianze,HU Tai,et al.Single-phase low harmonics saturated controllable reactor[J].Electric Power Automation Equipment,2007,27(7):17 -21.

