一种文化鱼群算法及其在电机参数辨识中的应用
吴莹,黄显林,高晓智,,Kai Zenger
(1.哈尔滨工业大学 控制理论与制导技术研究中心,黑龙江 哈尔滨150001;2.阿尔托大学 自动化与系统技术系,芬兰 赫尔辛基 FI-00076)
0 引言
人工鱼群算法(artificial fish-swarm algorithm,AFA)是一种基于自然界鱼群行为的群智能优化算法[1]。AFA算法通过模拟鱼觅食、群聚和追尾等行为,建立人工鱼群的简单的基本行为。AFA算法有较好的全局寻优性能,对搜索空间也有一定的自适应能力。然而由于人工鱼个体行为是寻找局部最优值,这种算法不可避免地会遇到个体早熟的难题,在处理多峰函数优化时容易陷入局部最优。为进一步提高AFA算法的全局收敛性能,本文提出在算法中引入变异因子,同时应用文化算法指导鱼群的进化。
文化算法(culture algorithm,CA)是一种新颖的处理优化问题的方法,由 Reynolds于 1994年提出[2]。CA算法包含了由人类社会文化发展规则发展出来的一类计算模型,是一个双向继承体系。从微观角度,群体空间中进行着鱼群进化;从宏观角度,个体在进化过程中得到的经验通过接收函数保存在信仰空间中,用于指导个体往更优解的方向进化。信仰空间和群体空间之间通过通讯协议联系,通讯协议决定了知识通过影响函数指导群体空间个体进化的方式。多种进化算法可以嵌入到文化算法框架中作为群体空间的进化过程[2-4]。
本文首先引入变异算子,将文化算法和AFA算法融合,提出了克服算法早熟缺点的带变异算子的鱼群算法——CAFAC(cultured AFA with crossover,CAFAC)。根据融合方式的不同,一共提出了4种CAFAC算法。将人工鱼群作为文化算法中的群体空间,利用信仰空间中的规划知识和情景知识指导鱼群进化的步长和方向。通过5个高维多峰函数检验算法的性能,最后应用新算法求解鼠笼式感应电机系统的参数辨识问题。
1 人工鱼群算法和文化算法
1.1 人工鱼群算法
人工鱼群算法的基本思想是模拟鱼的行为,例如觅食、群聚和追尾。假设D维优化问题,共有N条人工鱼,每一条人工鱼描述为:Xi=(xi1,xi2,…,xiD),i=1,2,…,N,其中 Xi表示要优化的变量,y=f(Xi)表示适应度函数,描述了人工鱼所在点的食物浓度,f(Xi)值越小说明食物浓度越低。AFA算法的主要参数有 dij=‖Xj-Xi‖表示人工鱼个体 Xi和Xj之间的距离;vvisual表示人工鱼个体的视野;sstep表示人工鱼个体移动步长;δ表示拥挤度因子。
人工鱼的行为描述如下[1]:
1)觅食行为:人工鱼当前状态为Xi,在其视野范围内随机选择一个状态Xj表示为Xj=Xi+rand(0,1)×vvisual,当该状态的食物浓度大于当前状态,即f(Xj)<f(Xi)时,则人工鱼向该方向前进一步,即
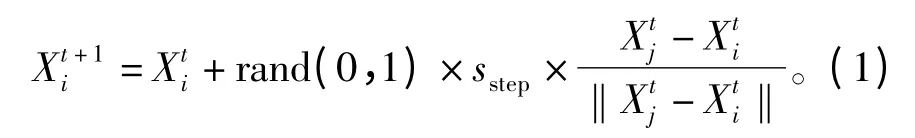
如果f(Xj)>f(Xi),则重新随机选择 Xi,判断是否满足前进条件;反复ntry-number次后,如果仍不满足,则随机移动一步,即
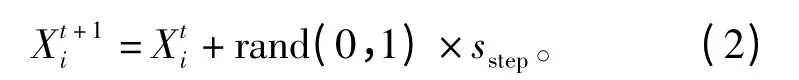
2)群聚行为:人工鱼当前状态为 Xi,在其视野范围内有nf个伙伴。如果nf≠0定义人工鱼群伙伴中心位置)表示中心位置的适应度值。如果nf×ycenter<δ×yi,则表明伙伴中心位置Xcenter不太拥挤,同时,如果中心位置的食物浓度大于当前状态的食物浓度,则人工鱼向Xc前进一步,即
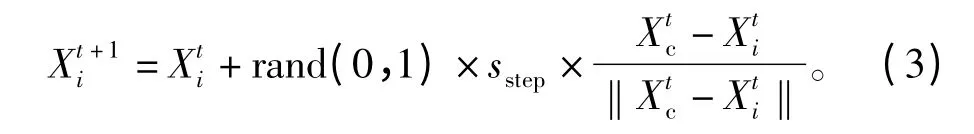
如果nf×ycenter<δ×yi,人工鱼执行觅食行为。
3)追尾行为:人工鱼当前状态为 Xi,在其视野范围内的最优伙伴是 Xmin,对应的食物浓度分别为ymin=f(Xmin)。nf表示 XminXmin视野范围内伙伴数目,如果 ymin<f(Xi),nf×ymin<δ×yi,则人工鱼向Xmin前进一步,即
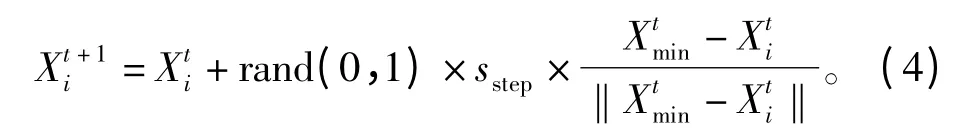
如果前进条件不满足,则执行觅食行为。
1.2 文化算法
Reynolds在1994年提出了文化算法这一概念,文化算法总体上包括三大元素:种群空间,信念空间和通讯协议,其中通讯协议又包括接收函数、更新函数和影响函数[5]。文化算法的基本框架[6]如图 1所示。
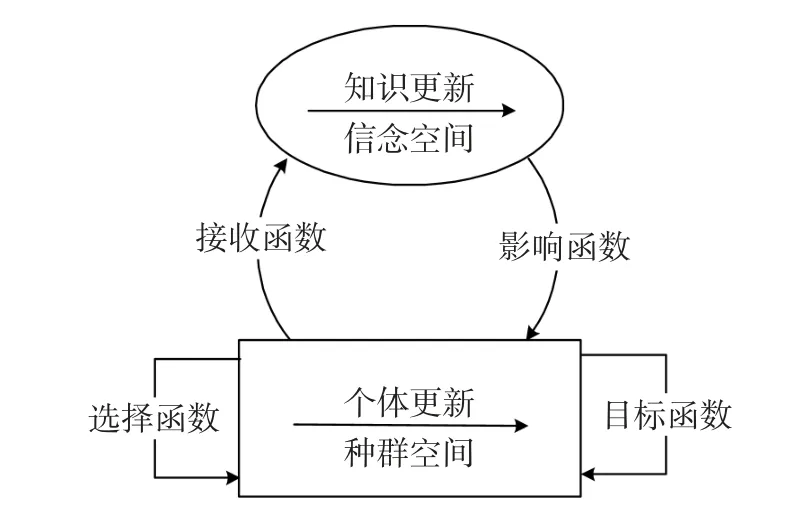
图1 文化算法框架Fig.1 Framework of cultural algorithm
2 带变异算子的文化鱼群算法
人工鱼群算法具有对初值、算法参数设置不敏感的特点。然而由于人工鱼进化行为和步长的随机性,算法在成熟阶段收敛很慢,特别是当解空间较大或者为平坦区时,算法存在搜索盲区,造成人工鱼群算法局部搜索能力和全局探索能力之间的失衡。针对这些不足,本文提出了一种新型的带变异算子的文化鱼群算法CAFAC,改进常规人工鱼群算法的优化性能。
首先在人工鱼群算法中引入变异算子改变人工鱼的状态,使人工鱼尽可能地搜索其他区域的可能的解。人工鱼找到食物后,通常会游向更好的方向。变异算子带来的探索行为不仅可以帮助人工鱼跳出搜索盲区,而且继承了父代的优势。
接下来受到文化算法思想的启发,在基本人工鱼群算法中应用信仰空间中保存的规划知识和情景知识指导人工鱼种群的进化步长和方向[7]。这样在信仰空间中形成和保存的域知识可以用来描述和指导种群的每一步进化行为,根据知识指导进化方式的不同,本文中提出了4种不同形式 CAFAC算法。
2.1 CAFAC算法中的信仰空间结构
情景知识只包含人工鱼群中的当前最佳个体,定义在第t步迭代的情景知识描述为。情景知识的初始值为初始种群中的最佳人工鱼个体,迭代过程中的更新方程可描述为
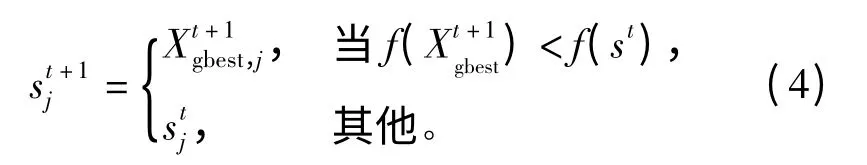
规划知识描述了优化问题的可行解空间[7]。每一个变量的规划知识表示为
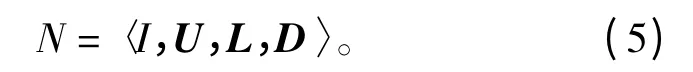
其中U、L和D 是n维向量,I={x|l≤x≤u},n表示变量个数;lj和uj分别是第j个变量的下界和上界,Lj和Uj是对应的适应度值。通常lj和 uj用初始种群的下界和上界初始化。在迭代过程中,规划知识按照以下公式更新,即
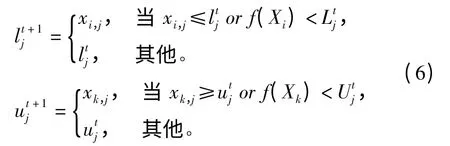
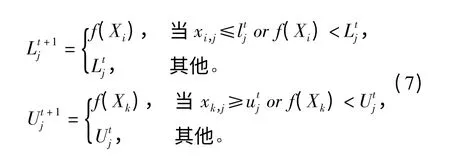
其中第ith个体影响第 j个变量的下界,第k个体影响第jth个变量的上界,t表示信仰空间当前的迭代步数。
2.2 CAFAC算法中的接收函数
接收函数的作用是确定种群中哪部分个体用来更新信仰空间中的知识。用于更新知识的个体数目可由下式确定[4],即
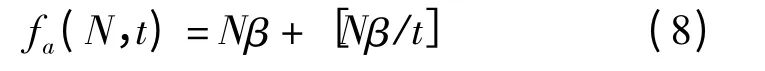
其中N是种群规模,t是当前迭代步数,β=0.2。
2.3 CAFAC算法中的影响函数
信仰空间的知识通过3种方式影响种群空间的个体进化:1)决定进化的步长。2)决定进化的方向。3)由规划知识确定决定前进步长,同时在视野范围内确定人工鱼个体下一步前进的方向。
利用规划知识和情景知识指导进化的步长和方向时,有4种不同的方式。如果规划知识仅用来决定前进步长,则新算法称为CAFAC(Ns);如果用情景知识来指导人工鱼个体的进化方向,则新算法称为CAFAC(Sd);如果利用规划知识指导人工鱼个体进化的步长,同时利用情景知识指导进化的方向,新算法称为CAFAC(Ns+Sd);如果利用规划知识同时指导人工鱼个体的进化方向和步长,则产生的新算法称为CAFAC(Ns+Nd)。接下来例举CAFAC(Ns+Sd)算法的影响函数,说明两种知识对人工鱼进化的指导作用。
在第k步进化时,利用情景知识指导进化的方向为
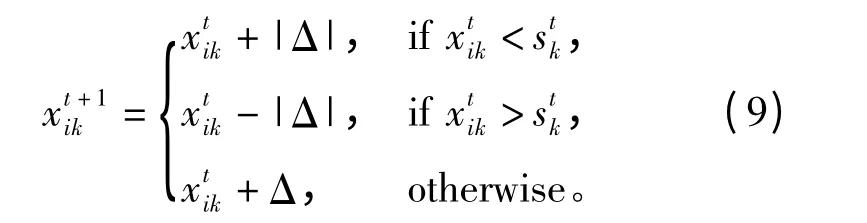
其中Δ描述了进化的步长,利用规划知识指导进化的步长。
1)觅食行为
当 i≤ntry-number时,
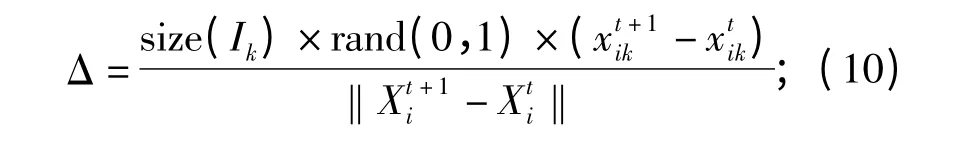
当 i> ntry-number时,
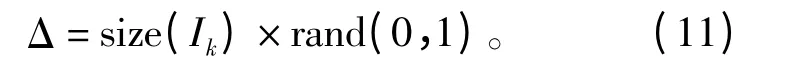
2)群聚行为
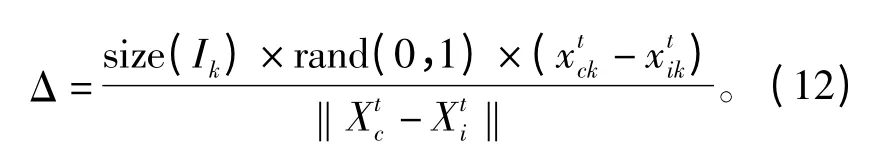
3)追尾行为
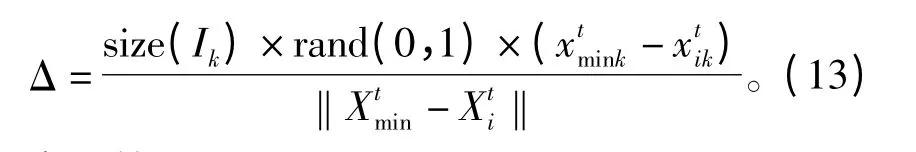
2.4 变异算子
根据以下准则判断CAFAC算法是否陷入局部最优:
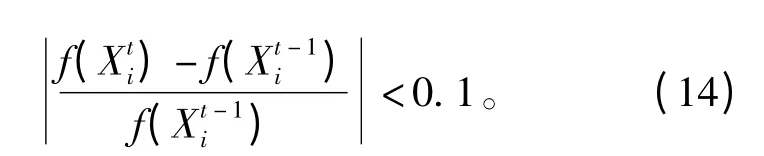
当以上判断准则成立时,对第 i个人工鱼Xi(i=1,2,…,N)执行变异操作[8]:
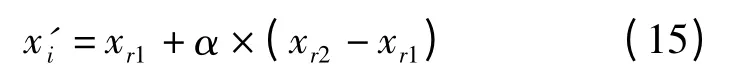
其中:xr2,xr1是随机挑选的两个人工鱼个体,r1,r2是[1,N]区间里的两个随机整数,并且满足r1≠r2≠i;α是[-d,1+d]中满足均匀分布的随机数,其中d=0.25;评价子代 x'i,如果优于父代,则用 x'i替代xi。
本文提出的新算法CAFAC的基本流程可以描述如下:
1)初始化人工鱼个体的数目N,人工鱼视野范围、拥挤度因子等算法参数,设置迭代次数和收敛条件,初始化N个人工鱼个体的位置;
2)评价所有人工鱼个体,计算适应度函数值,初始化信仰空间;
3)对每一个人工鱼个体,比较觅食、群聚和追尾三种行为,选择其中最好的子代,如果对应的适应度函数值优于父代,则用子代替代父代;
4)更新信念空间;
5)如果满足不等式(14),则对第3步中的人工鱼个体执行变异操作;
6)判断是否满足收敛条件,如果不满足则回到第3步直到满足算法收敛条件。
3 高维多峰非线性函数优化
选取5个高维、多峰非线性函数检验新算法CAFAC的性能,包括4种算法形式CAFAC(Ns),CAFAC(Sd),CAFAC(NsSd)以及CAFAC(NsNd)。分别为fAckley(x)=
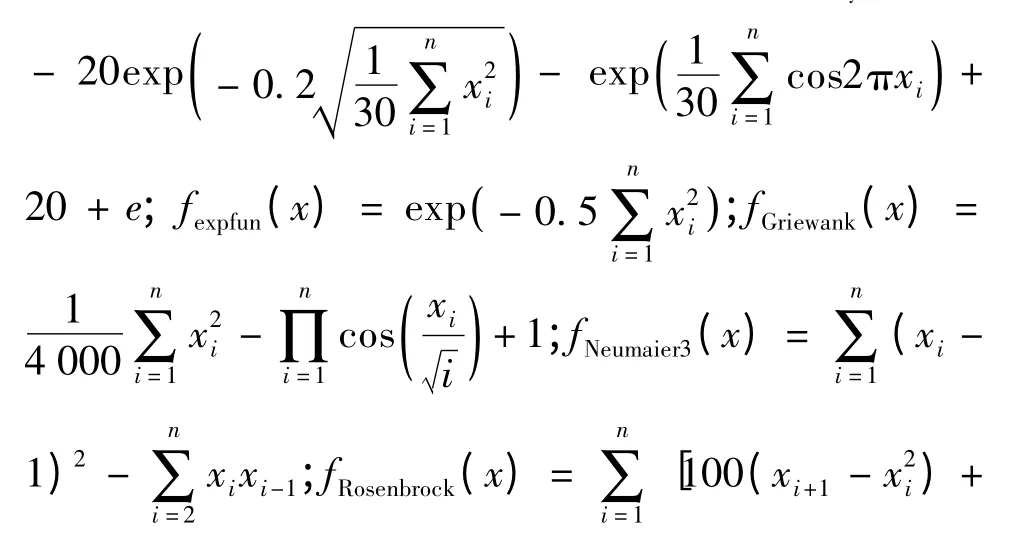
(xi- 1)2;;参数设置如下:N=40,D=30,vvisual=250,sstep=225,δ =24,ntry-number=10。测试函数的维数均为30。
算法分别运行 10次,每一次迭代 5 000步。CAFAC算法的性能与基本鱼群算法AFA的比较结果如表1所示。从表中可以看出,对于 Expfun函数、Griewank函数和 Neumaier3函数,算法 CAFAC(NsSd)可以准确地找到全局最优值。对于Ackley和Rosenbrock函数,所有的4种CAFAC算法的性能都较AFA算法有明显提高,体现了新算法全局优化性能有了显著的改善。从表1中还可以看到CAFAC(NsSd)算法的性能总体上优于其他3种算法,由此可以推断利用信仰空间中的知识指导鱼群进化的方向和步长可以取得最佳的优化性能。
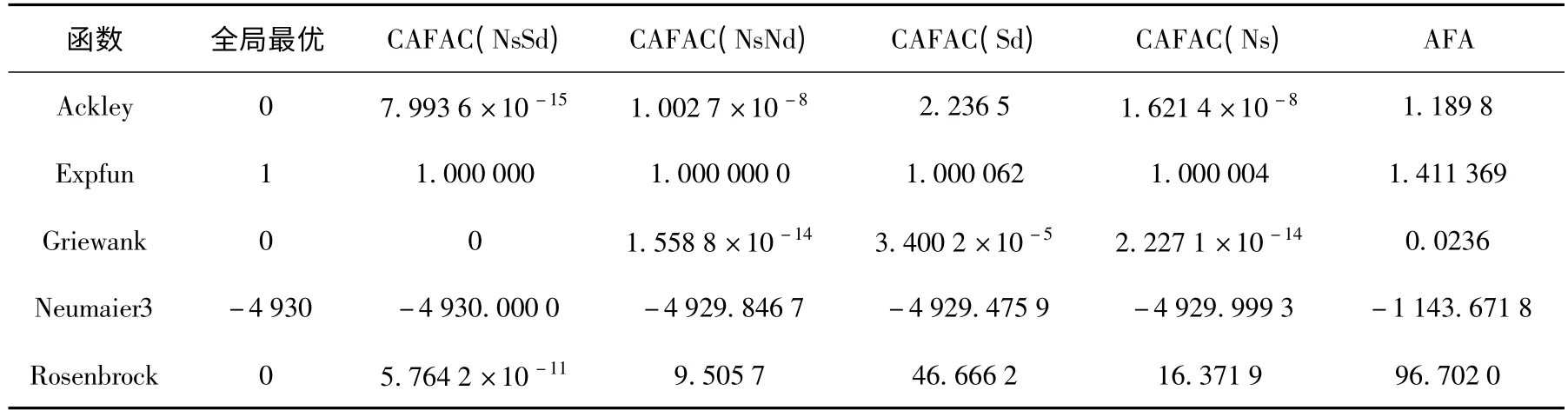
表1 CAFAC算法与AFA算法函数优化性能比较Table 1 Performance comparison for CAFAC and AFA
以 Ackley和Rosenbrock函数为例,图2、图3比较了4种CAFAC算法的收敛性能。为了便于比较,图中纵轴是采用了对数坐标,横坐标每50步画一个数据。平均适应度函数值是算法10次独立运行对应的适应度值的平均值。从图上可以看出,AFA算法在迭代初期收敛很快,但是随后便陷入局部最优。CAFAC算法较好地客服了AFA算法的这一不足,提高了人工鱼群算法跳出局部最优的能力,提高了全局寻优性能。
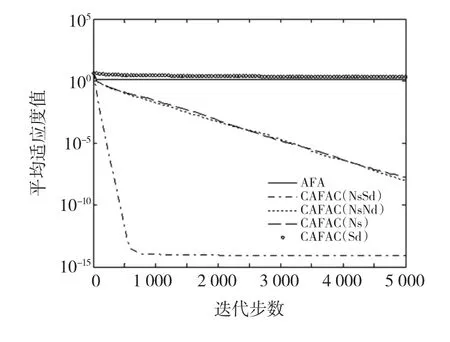
图2 Ackley函数的优化结果Fig.2 Results of Ackley function

图3 Rosenbrock函数的优化结果Fig.3 Results of Rosenbrock function
4 笼式感应电机参数辨识
4.1 问题描述
本节中研究的笼式感应电机,在定子上绕有4极绕组起到执行器的作用。执行器产生作用于转子的力,抑制转子轴在水平和垂直方向的振动偏移。电机辨识系统中利用电涡流传感器测量电机转轴的振动偏移量,编码器用于测量转子转动角度和频率。电机系统参数辨识的目的是建立电机系统的数学模型,在此基础上设计系统主动振动控制器。电机工作频率32.085 Hz,激励信号(水平和竖直方向的控制电压)是一个均匀分布的随机数序列,频率最高500 Hz。输出信号经过处理,只保留激励信号引起的系统响应[9],如图4所示。图4中前13 s记录的数据用于参数辨识,剩余的数据用作测试数据。
研究电机系统的线性时不变参数模型,根据文献[10],感应电机模型建立在模态坐标系中的机械模型基础上[11]:
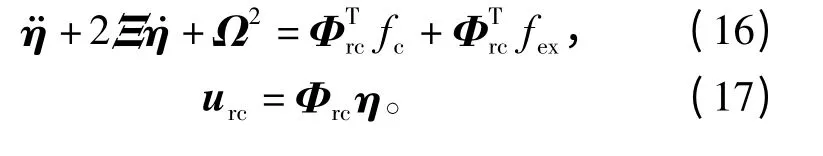
其中:η表示模态坐标系中的向量;urc表示转子轴中心偏移量;Φrc表示模态矩阵;Ω表示包含固有频率的对角阵;Ξ表示包含不同频率对应的阻尼系数的模态阻尼矩阵;fex表示干扰力;fc表示作用在转子上的机电控制力。
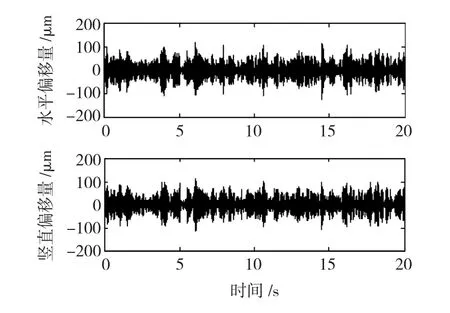
图4 转子偏移实测值Fig.4 Measurements of rotor displacement
模型结构与文献[12]中相同,表示为
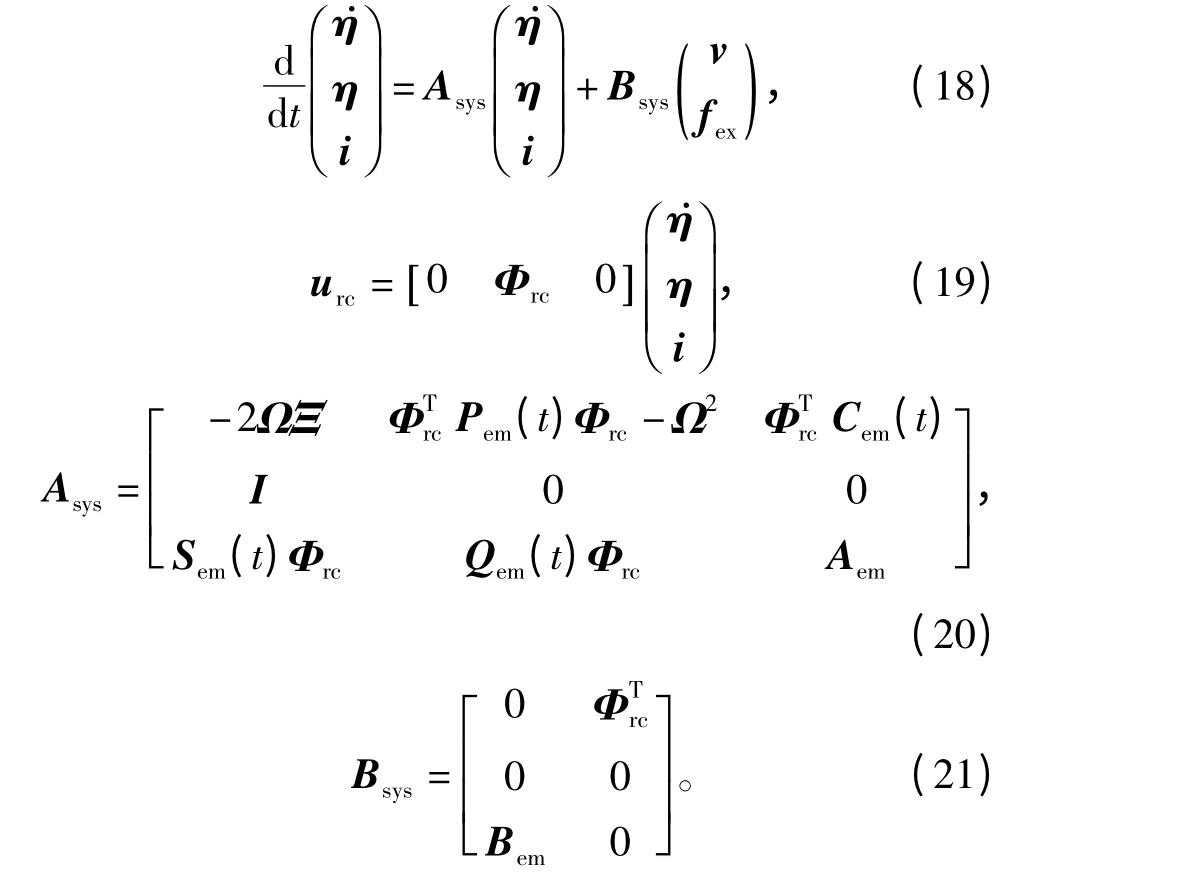
其中各个矩阵定义如下:
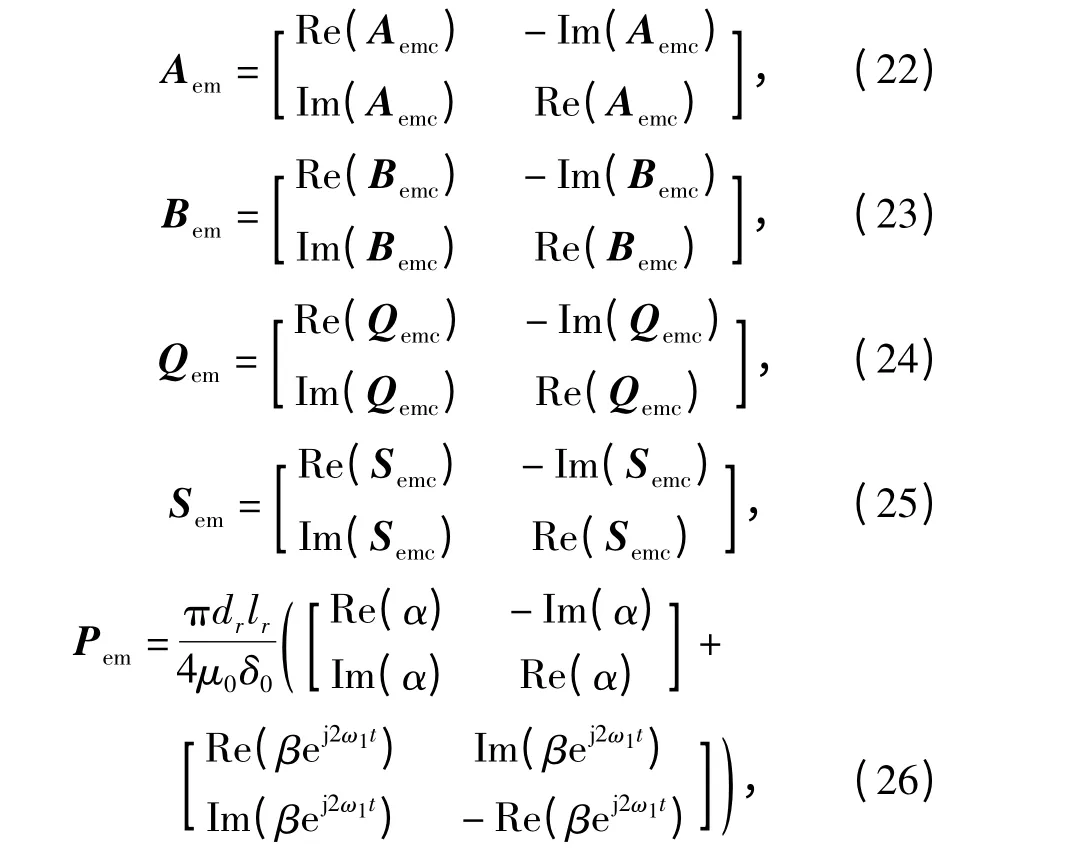
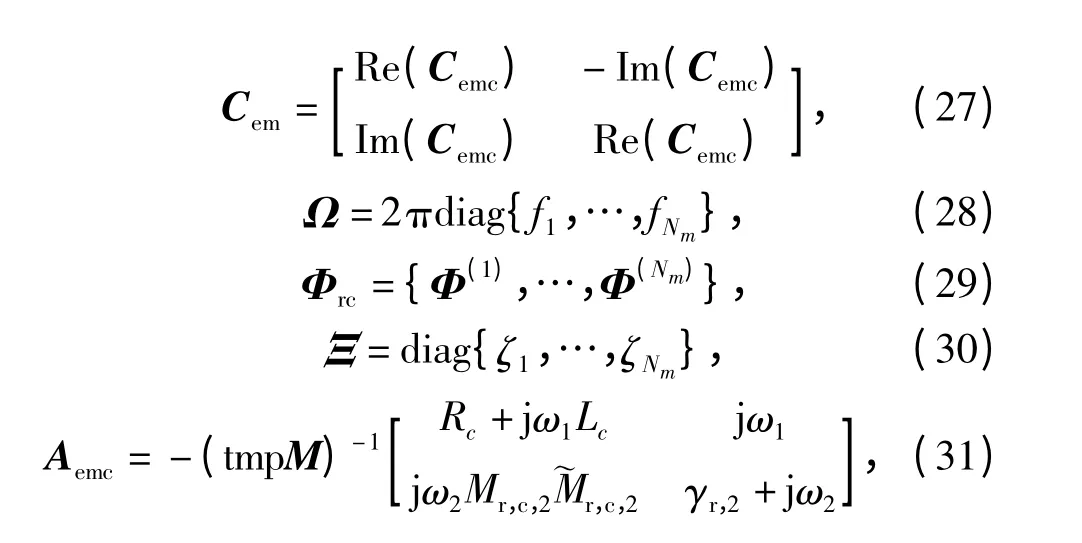
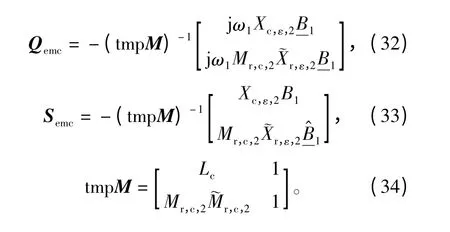

表2 电机系统参数Table 2 Parameters of motor system
电机系统线性时变模型的参数如表2所示,满足一定的物理约束。电阻值已知且是常数,Rc=14.5,无需优化。当不考虑不平衡磁拉力的作用时,模型简化为一个线性时不变系统。输入量包含控制绕组电压υ,输出量是转子中心的偏移量urc。系统矩阵是未知参数的函数,未知参数的含义和电机系统模型的详细推导见文献[12],将未知参数表示为如下向量:
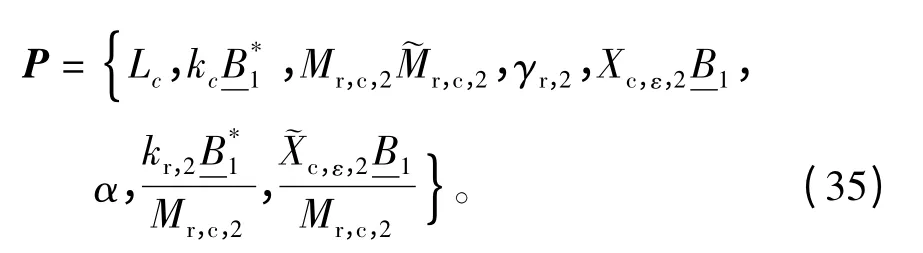
4.2 利用CAFAC算法辨识电机系统参数
参数辨识过程中,利用电压υ和干扰力fex激励系统。为了降低系统阶次,从辨识测量数据中去掉干扰力,即fex=0。辨识目的是建立系统参数模型,在保存的有限带宽白噪声激励下,模型的输出与实际系统的输出信号吻合。参数辨识的基本思路是找到一组向量使得以下代价函数的值最小[15],即
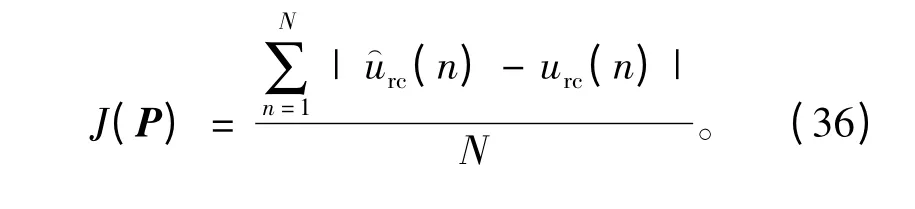
其中urc(n)表示电机系统在特定输入下的输出信号测量值(n)表示同样输入下,辨识得到的参数模型的输出。定义一个评价指标衡量得到的模型参数P的准确性,即
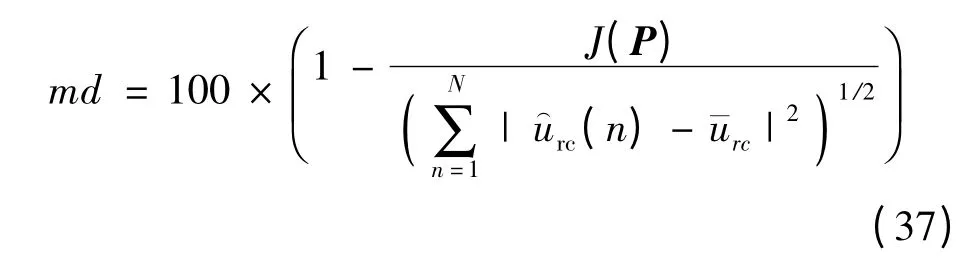
在之前的CAFAC算法的仿真算例结果分析中,发现CAFAC的4种形式中 CAFAC(NsSd)算法的性能优于其他3种形式,并且显著优于基本鱼群算法AFA[14]。因此利用CAFAC(NsSd)算法进行电机系统参数化模型辨识。参数辨识结果如表3所示。利用测量数据的13~20 s的数据检验辨识结果,最终辨识模型的输出和实际系统的输出对比结果如图5所示,为了显示清晰截取了15~16 s之间的对比结果。水平方向和竖直方向的模型匹配度分别为78.9400%和84.9011%。可以看出利用CAFAC算法得到的辨识模型有效地描述了实际系统的特性,参数模型的响应与实际系统输出间的偏差接近于零。
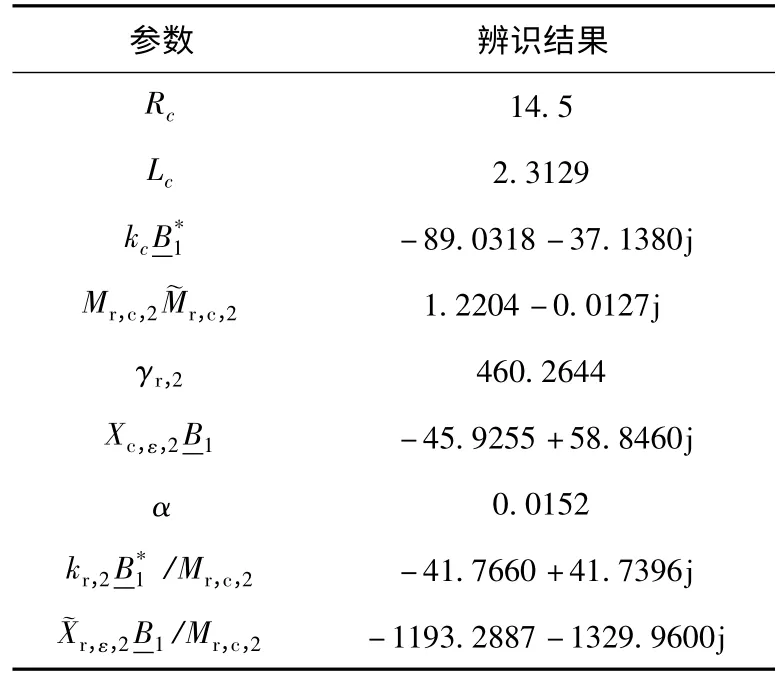
表3 电机系统辨识结果Table 3 Identification results of motor system
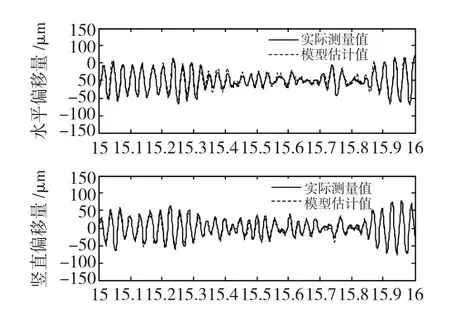
图5 实际系统与辨识模型对比Fig.5 Comparison of outputs between the real system and estimated model
5 结论
基本人工鱼群算法AFA在处理高维非线性优化问题时,容易陷入搜索盲区。本文提出了新算法CAFAC,引入了文化算法框架,利用存储在信仰空间的规划知识和情景知识指导人工鱼群的进化;变异算子的引入提高了人工鱼群的多样性,有助于算法跳出局部最优,新算法提高了人工鱼群算法的全局优化性能。
通过高维多峰函数优化问题检验了新算法性能,结果表明本文提出的基于知识和变异算子的CAFAC算法相较基本鱼群算法,全局优化性能有了显著提高。最后利用CAFAC算法进行了内置执行器的笼式感应电机系统的参数辨识,结果表明辨识得到的参数化执行器-转子系统模型有效地体现了实际电机系统的响应特性,具有很高的匹配度。本文的研究结果表明CAFAC优化算法在函数优化以及高维非线性系统参数辨识领域具有很好的应用前景。
[1]LI X L,SHAO Z J,QIAN J X.An optimizing method based on autonomous animates:fishswarm algorithm[J].Systems Engineering Theory and Practice,2002,(11):32 -38.
[2]REYNOLDS R G.An introduction to cultural algorithms[C]//The 3rd Annual Conference on Evolution Programming,February 24 -26,1994,San Diego,CA.1994:131 -139.
[3]CHUNG C J,REYNOLDS R G.A test-bed for solving optimization problems using cultural algorithms[C]//Evolutionary Programming V:The Fifth Annual Conf.on Evolutionary Programming,February 29 - March 3,1996,San Diego,CA.1996:225 -236.
[4]REYNOLDS R G,CHUNG C J.Knowledge-based self-adaptation in evolutionary programming using cultural algorithms[C]//IEEE International Conference on Evolutionary Computation,April 13-16,1997,Indianapolis,Hoosier State.1997:71 -76.
[5]CHUNG C J.Knowledge-based approaches to self-adaptation in cultural algorithms[D].Detroit:Wanyne State University,1997.
[6]GAO X Z,JOKINEN T,WANG X,et al.A new harmony search method in optimal wind generator design[C]//The XIX International Conference on Electrical Machines,September 6 -8,2010,Rome,Italy.2010:1 -6.
[7]REYNOLDS R G,PENG B.Cultural algorithms:modeling of how cultures learn to solve problems[C]//The 16th IEEE International Conference on Tools with Artificial Intelligence,November 15 -17,2004,Boca Raton,FL.2004:166 -172.
[8]WANG X P,CAO L M.Genetic Algorithm:Theory,Application and Software Implementation[M].Xi’an:Xi’an JiaoTong University Press,2002.
[9]SINERVO A.Modeling and control of flexural rotor vibration of a two-pole cage induction motor[D].Espoo:Helsinki University of Technology,2008.
[10]ORIVUORI J,ZENGER K,SINERVO A.Active control of rotor vibrations by advanced control methods[C]//The 16th International Congress on Sound and Vibration-Recent Developments in Acoustics,Noise and Vibration,July 5 -9,2010,Krakow,Poland.2010:1-8.
[11]LAIHO A,TAMMI K,VIDQUIST V,Modeling of flexural rotor vibration and time-periodic system dynamics in a two-pole cage induction machine equipped with a self-bearing force actuator[C]//The IFAC Workshop on Periodic Systems,Bogazici University,August 26 -28,2010,Turkey.2010.
[12]Genta G.Vibration of Structures and Machines:Practical Aspects[M].NY:Springer,1999.
[13]Holopainen T P,Tenhunen A,Lantto E,et al.Unbalanced magnetic pull induced by arbitrary eccentric motion of cage rotor in transient operation.Part 1:analytical model[J].Electrical Engineering,2005,88(1):13 -24.
[14]GAO X Z,WU Y,ZENGER K,et al A knowledge based artificial fish-swarm algorithm[C]//The 13th IEEE International Conference on Computational Science and Engineering,December 11-13,2010,Hongkong,China.2010:327 -332.

