增强型Z源逆变器的直流链电压直接控制策略

蔡春伟， 曲延滨， 盛况

(哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨150001)

0 引言

Z源逆变器在输入电源和逆变桥之间加入特殊的X型LC网络，利用桥臂直通提高直流链电压，具有单级实现升/降压的功能。同桥臂直通成为常态，逆变器的抗干扰能力得到提高;不再需要死区时间，逆变器的输出质量得到改善［1－2］。但是传统Z源逆变器存在升压能力弱、Z源电容电压应力过大等缺点，近几年来，人们提出两类改进型Z源逆变器拓扑，都以不同的结构实现了更高的电压增益［3－5］，其结构可分为级联式和串联式。文献［6］提出一种增强型高增益Z源逆变器，改进后的Z源逆变器的升压能力有了很大提高，电容电压应力也得到减小，有利于减小电容的体积和降低逆变器的成本。

为了研究Z源逆变器的内在特性，文献［7－8］建立了Z源逆变器直流侧的小信号模型。对于Z源逆变器来说，由于交流侧可以采用传统电压源逆变器的控制策略，因而直流链电压的控制成为Z源逆变器控制策略中一个重点的研究内容。直流链电压的稳定对逆变器的输出质量有着直接的影响，为了抑制输入电源电压波动和负载变化对直流链电压的影响，在小信号模型的基础上，文献［9－15］研究了相应的反馈控制策略，可以分为两种:一种是电容电压反馈控制，另一种是直流链峰值电压反馈控制。对于电容电压反馈控制策略［9］，虽然电容电压保持不变，但电容电压并不等效于直流链峰值电压，两者之间存在着非线性的关系，因此直流链峰值电压随着直通比的变化而波动，增加了直流侧的控制难度。而直流链峰值电压直接控制虽然提高了控制精度，降低了交流侧控制策略的难度，但直流链电压是脉冲方波信号，给系统的直接检测、反馈控制带来很大的麻烦。文献［10］介绍一种峰值电压检测电路，并在其基础上采用直流链峰值电压作为反馈信号进行单闭环控制，但是由于其峰值检测电路是二阶滤波电路，不但增加了设计的复杂性，而且给反馈信号带来很大的时滞，增加了控制器设计的难度;另外由于受到其右平面零点的影响，采用单闭环控制器虽然能够将系统校正为稳定的，但是其动态特性不很理想;并且其控制器的设计是基于直流链电压与直通比的传递函数设计的，而直流链电压的交流小信号与直流链峰值电压的小信号是不等价的，所以其控制器的设计也存在一定的误差。文献［11－12］提出间接峰值电压控制策略，通过稳态Z源电容电压与直通占空比之比来计算直流链电压，这种方法虽然比Z源电容电压控制精度有所提高，但是仍然是一种间接控制，其控制精度和动态性能都不如直流链峰值电压直接控制。

为了提高Z源逆变器直流链电压的控制精度、改善系统的动态性能，本文在对增强型逆变器的直流链电压的小信号分析的基础上，构建以直流链峰值电压作为外环、Z源电感电流为内环的双闭环控制的控制方式。外环以直流链峰值电压作为反馈信号，利用电容电压和输入电压预估直流链峰值电压，能够减少直流链峰值电压测量电路的复杂程度;内环是Z源电感电流为反馈信号，增加系统的响应速度，改善其动态特性;直接基于直流链峰值电压的小信号模型设计双闭环控制器，有效地削弱控制至输出的传递函数中右平面零点带来的非最小相位的影响，提高系统的动态响应速度和控制精度。

1 增强型高增益Z源逆变器及其小信号建模

增强型高增益Z源逆变器如图1所示［6］，采用L1－L3－D1－D3－D5组成第一路电感单元，L2－L4－D2－D4－D6组成第二路电感单元，分别代替传统Z源逆变器的两个电感，利用非直通时同一支路两电感串联来提高直流链升压能力。

图1 电压型高增益Z源逆变器Fig.1 Voltage fed quasi-Z-source inverter

1.1 电路分析

假设L1=L2=L3=L4=L，C1=C2=C，这样Z 源网络就是对称的，所以有vC1=vC2=v，iL1=iL2=iL3=iL4=iL。与传统Z源逆变器一样，新型Z源逆变器也有两种开关状态:直通和非直通状态。在非直通状态(包括有效和零矢量)，等效电路图如图2(a)所示，忽略二极管压降，可得

式中:vi是直流链电压;vPN是直流链峰值电压;Vin是输入电压。

图2(b)所示，在直通状态下，逆变器侧被短接，可得

由于稳态时单周期内电感两端的平均电压为零，可得

直流链电压峰值可表示为

式中D是直通占空比，可以看出该拓扑的升压能力远高于传统拓扑。图3给出了增强型Z源与传统Z源直流链升压因子与直通占空比的关系曲线，由图3可以看出，增强型Z源网络的升压能力相比于传统Z源网络有了很大的提高，以直通占空比D=0.3为例，传统网络的直流升压比B=2.5，而增强型网络的升压因子B′=13。

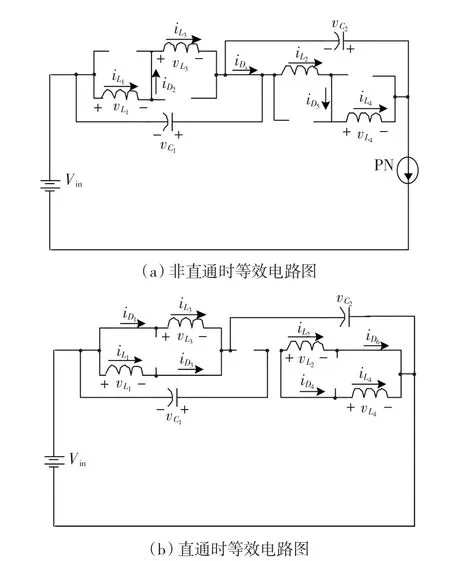
图2 高增益Z源逆变器的等效电路Fig.2 Equivalent circuit of improved Z-source inverter

图3 传统Z源网络与增强型Z源网络升压能力对比Fig.3 Boost ability comparison of the traditional Z-source network and the proposed one

1.2 交流小信号建模

信号流图由于使用较少的数学变换就能够推导出不同的控制对输出及扰动对输出的传递函数，是为Z源逆变器建模的一种很好的工具［8］。

考虑电感内阻和电容等效电阻，有

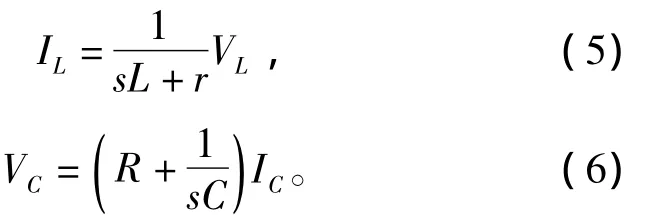
式中:r是 L1、L2、L3、L4电感的内阻;R 是 C1、C2的等效电阻(ESR)。

把式(1)～式(6)用信号流图表示出来，在所有的稳态变量中引入小信号变量，图4是交流小信号流图。由图4所示，利用梅森公式［5］，可以获得/的传递函数Gvd(s)如式(7)c/in的传递函数Gvg(s)如式(8)。式(7)含有一个右平面零点，说明该系统属于非最小相位系统。根据式(7)、图4，建立系统的简化框图如图5。

图4 增强型Z源网络的信号流图Fig.4 Graphical signal-flow representation of the enhanced Z-source impedance network

图5 增强型Z源网络的框图Fig.5 Block diagram representation of the enhanced-Z-source impedance network

2 以电容电压反馈的控制策略

文献［9］最早提出传统Z源逆变器Z源网络电容电压作为反馈信号控制直流链电压，电容电压与直流链峰值电压的关系是VPN=Vc/(1－D)，由于直通比D的存在，虽然采用PID策略能够保证电容电压恒定，但是却无法得到恒定的直流链电压。

随后文献［11－12］提出采用电容电压与非直通占空比的比值作为反馈信号，建立直流链电压闭环控制，这样能够保证稳态时直流链电压是稳定的。

但是Vc/(1－D)只是一个稳态结果，它并不能完全反映直流链电压的动态过程，以增强型Z源拓扑为例，根据式(3)、式(4)，电容电压与直流链峰值电压的关系是

图6是直通比D=0.2，直流输入电压在t=0.1时由120 V变为150 V，(1+D)Vc/2D与VPN的响应曲线。

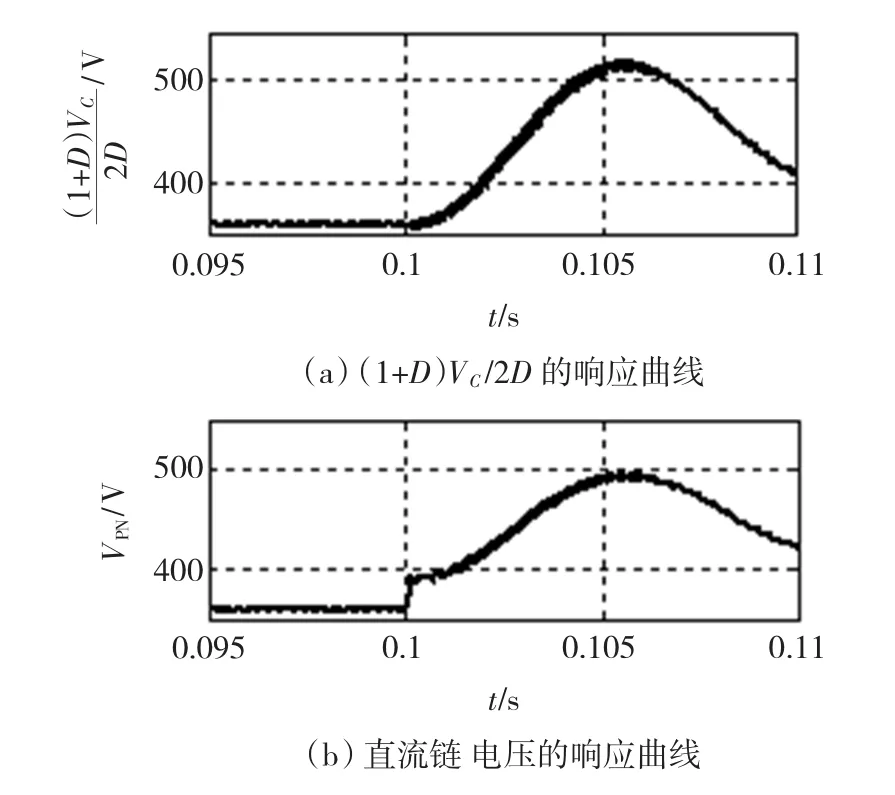
图6 对输入电压阶跃变化的仿真结果Fig.6 Simulated results for step change in the input voltage

从图6可以明显看出在输入电压刚开始变化时，VPN马上有个阶跃的增长，而(1+D)Vc/2D没有及时反映，而是滞后很长时间才阻尼增长，并且其振荡幅度也比直流链电压要大，因此(1+D)Vc/2D虽然能够反映直流链电压稳态值，但是无法反映输入变化引起的直流链电压的动态变化过程。所以采用(1+D)Vc/2D作为反馈信号的控制系统对直流链电压的动态响应速度和控制精度并不理想。并且从式(10)可以看出，直通比直接出现在分母上及除法的引入势必会增加直流链控制的难度，因此该拓扑不宜采用式(10)作为直流链电压反馈信号建立闭环控制系统。

3 直流链电压直接控制

3.1 直流链电压小信号分析

在其平均值上分别引入直流链电压vi、直通比D、直流链峰值电压vPN的扰动，代入式(11)可得

根据式(1)，直流链峰值电压vPN的扰动可表示为

由图3可以看出，vc的动态特性是由d和vin线性组合而成的

式中Gvd(s)是直通比至Z源电容电压的传递函数如式(7)，Gvg(s)是输入至Z源电容电压的传递函数如式(8)。将式(14)代入式(13)，获得直流链峰值电压vPN的小信号表达式

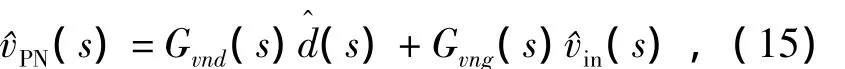
其中:Gvnd(s)=2Gvd(s);Gvng(s)=2Gvg(s)+1。

为了提升热力公司的基层党建工作的水平，发挥党建工作的重要作用，本文进行了如何以科学的思维方式和思想方法开展党建工作的研究，首先介绍了党建工作对于热力公司的重要作用，然后阐述了热力公司基层党建工作中现存的问题，最后提出了以科学的思维方式和思想方法开展热力公司党建工作的实施策略。经过近一年的党建工作实践，发现利用该策略能够有效地激发职工投身热力事业的积极性，有效地提高热力公司的向心力，有效地促进热力公司的健康发展，具有一定的推广价值。

式(15)可以通过比较小信号模型和开关电路的仿真波形来验证。为满足直流链电压纹波要求及输出电压纹波要求，所采用的参数:直流输入电压Vg=120 V，Z 源电感 L=500 μH，Z 源电容 C=680 μF，滤波电感L=3 mH，滤波电容C=10 μF，每相负载电阻Rload=46 Ω，开关频率fs=7.2 kHz，直通占空比D=0.2，调制比 M=0.75。

图7和图8分别是小信号模型的直流链电压与开关电路的非直通时直流链电压对于直通比和输入电压的阶跃变化的响应曲线，可以验证从开关电路测量的直流链电压vi和平均模型的vPN具有同样的动态特性。

从式(15)中很明显可以看出直流链峰值电压对于直通占空比的传递函数Gvnd(s)与电容电压控制函数Gvd(s)有着线性关系，这说明两者应具有同样的动态特性。这也可以从图7(b)和图7(d)得到验证，从图中可以看出在直通占空比阶跃变化时电容电压与直流链峰值电压具有同样振荡，只是电容电压的变化是直流链的一半。

图7 直通比D由0.2变为0.25时开关电路与平均模型电路的仿真波形Fig.7 Simulation waveform from the switching circuit and the averaged model circuit when both circuits were subjected to step change form 0.2 to 0.25 in D

同样，由图8(b)和图8(d)也分别展示了直流链电压和电容电压在输入电压阶跃变化时的响应，直流链电压在输入发生阶跃变化后立刻有一个正的阶跃，紧接着是一个阻尼震荡，其震荡幅值是电容电压阻尼振荡的两倍，由此可以验证Gvng(s)=2Gvg(s)+1。

图8 输入直流电压由120 V变为150 V时开关电路与平均模型电路的仿真波形Fig.8 Simulation waveform from the switching circuit and the averaged model circuit when both circuits were subjected to step change form 120 V to 150 V in input voltage

3.2 直流链峰值电压检测方法

根据式(13)，直流链峰值电压是由电容电压和输入直流电压线性组合而成，采用文献［13］提出的测量方法成比例的测量直流链峰值电压，如图9所示，图中R1=R2=R。

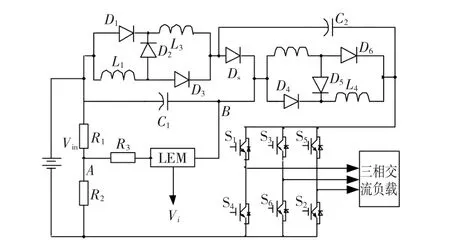
图9 直流链峰值电压直接检测电路Fig.9 Direct sampling circuit of DC-link peak voltage

根据基尔霍夫电流定律，对于图9中节点A有

整理，将式(14)带入式(17)，可得

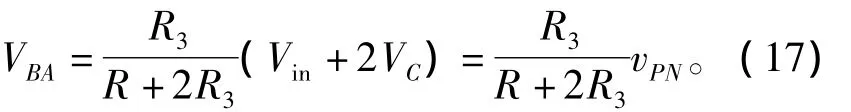
由式(17)可知，VBA与vPN成正比，因此可以通过测量AB两点电压获得直流链峰值电压。本文电阻取R1=R2=20 kΩ，R3=12 kΩ，则直流链峰值电压vPN与 VBA关系为

3.3 控制策略

文献［15］根据式(15)建立了直流链电压单闭环直接控制，框图如图10。对于单闭环控制采用PID控制器Gc(s)，将控制器的补偿零点放在ZSI的谐振极点附近;为了提高系统的带宽，选择高频率补偿极点在截止频率的10倍频。

图10 直流链电压单闭环控制框图Fig.10 Block diagram representation of the DC-LINK voltage single loop

从图11可以看出，由于右平面零点离原点太近，虽然采用PID控制能够将系统校正为稳定系统，但是其穿越频率太低、中频带宽太窄，因此系统的动态响应慢，控制效果不理想。

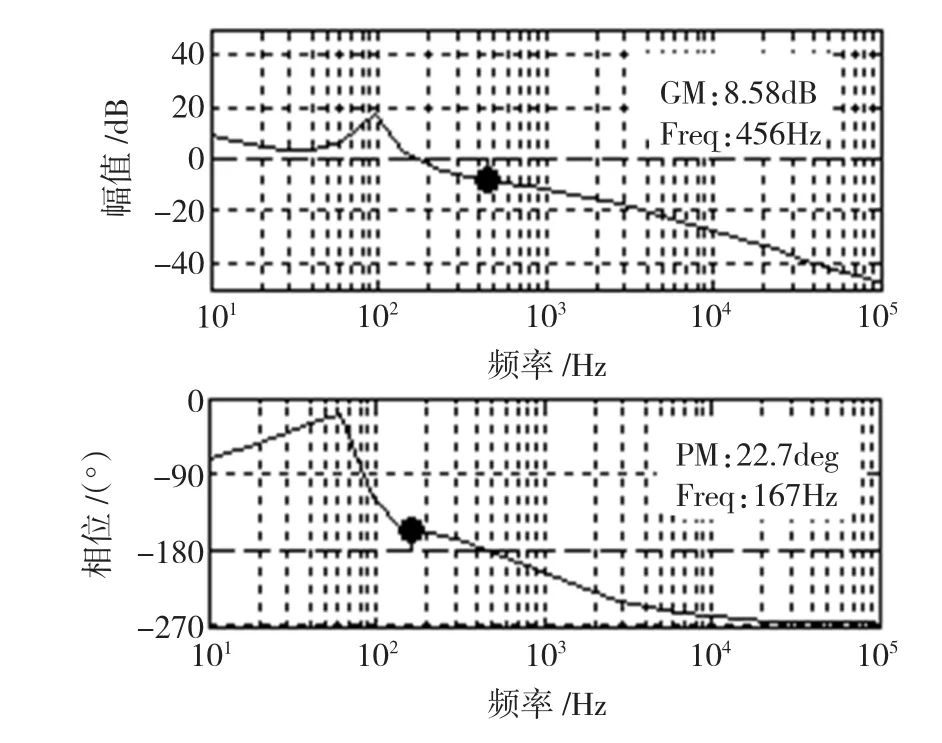
图11 单闭环系统的波特图Fig.11 Bode plots of single loop controlled system

众所周知，传统DC/DC变换器比如 Boost电路、Buck－Boost电路中也是类似的非最小相位系统，为了提高系统的动态响应、减小右平面零点对系统的影响，采用电流内环控制和电压外环控制的双闭环控制，因此本文也采用类似的方法来获得稳定反馈控制系统。由图4可以推导出电流内环的开环传递函数如式(19)，从式中可以看出其开环传递函数没有右平面零点，内环比较好控制，故采用比例控制器。而外环的开环传递函数如式(20)，为了稳定输出、获得足够的带宽，外环采用PI控制器，利用直流链峰值电压构成反馈，生成内环的电流指令信号，图12是Z源阻抗网络电流内环、电压外环控制的控制框图。

图12 直流链电压、电感电流双闭环控制框图Fig.12 Block diagram representation of the DC-LINK voltage and inductor current double loops

从图13可以看出，采用双闭环控制后系统的相角裕度有了很大提高，因此虽然截止频率wc没有太大变化，但是根据过渡过程时间ts=Kπ/wc，式中K随相角裕度的增大而减小，同样能够减小系统反应时间。低频段增益、斜率都增大从而减小了稳态误差。

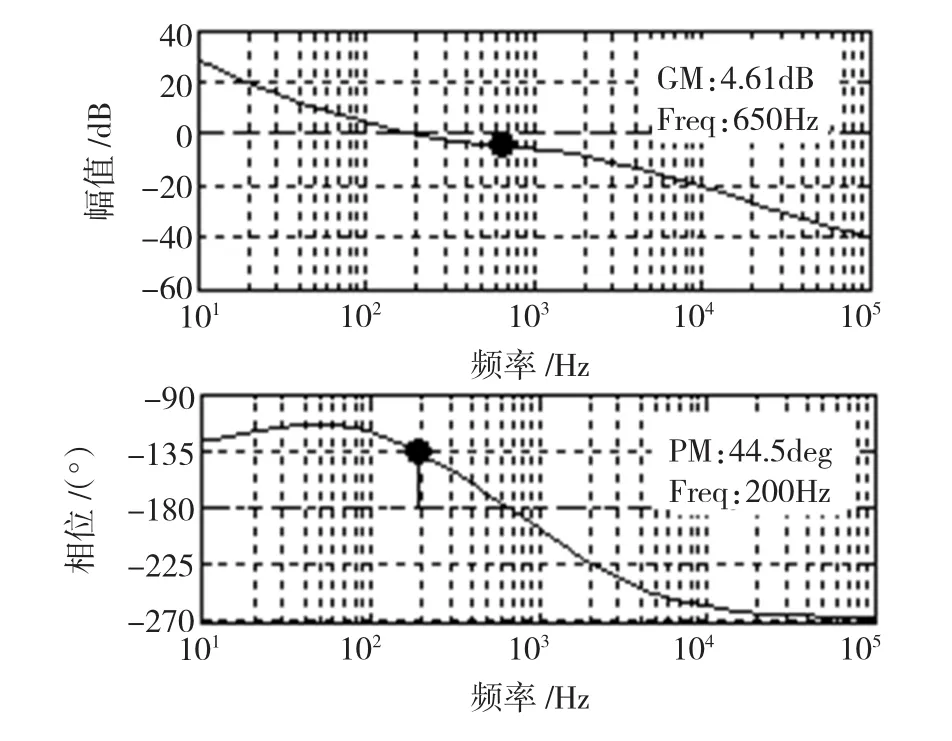
图13 双闭环系统的波特图Fig.13 Bode plots of double loops controlled system

4 仿真分析

图14 输入电压跌落20%的仿真结果Fig.14 Simulated results for step change in the input voltage 20%decrease

为了验证直流链峰值电压的控制策略，在3.1节所示的额定电路参数下对系统进行了仿真研究。首先验证对输入扰动的抑制能力，在0.15 s时输入电压由150 V降为120 V，控制器通过调整直通占空比来保证直流链峰值电压恒定，图14中自上之下分别是电路中输入电压、电容电压、电感电流、直流链峰值电压、交流输出电压的变化情况，可见在双闭环的作用下，直流链峰值电压并没有产生明显负超调，在很短的时间就恢复稳定，这是由于双闭环系统有足够的带宽来抑制非最小相位对系统的影响。

图15是负载在0.2 s时突然增加80%的仿真结果，从图中可以看出虽然交流侧是开环控制，但是输出交流电压波形表明直流侧控制系统抗负载的扰动能力很强。

图15 负载增加80%的仿真结果Fig.15 Simulated results for step change in the load 80%increase

5 实验验证

在实验室搭建实验样机验证控制算法，主电路参数如3.1节所示，采用基于SVPWM的Z源调制策略，图16是系统对直流输入阶跃扰动的抑制结果，当输入电压Uin由150 V跌落为120 V时，图16(a)观察可得与直流链峰值电压成比例的UAB保持恒定不变，而从图16(b)可以看出由于输入电压降低Z源逆变器的直通比增大导致Z源电感电流增大，从图16(c)、图16(d)看出直流链电压、交流输出受到的影响很小，因此系统对电压输入扰动有较强的抑制能力，但是由于输入变化是由自耦调压器调节产生的，不能达到仿真时的突变。

图17是系统对交流负载突然由46 Ω增大到25 Ω的抑制结果，从图17(a)可以看出输出电流突然增大但与直流链峰值电压成比例的UAB稍微跌落马上恢复，图17(b)当负载电流增大时Z源电感电流立即增大但是输出电压保持不变，从图17(c)、图17(d)可以看出直流侧峰值电压、逆变器输出电压虽然稍微有点跌落，但马上恢复，由图16、图17可以看出系统对输入、输出扰动都有很强的抑制能力。

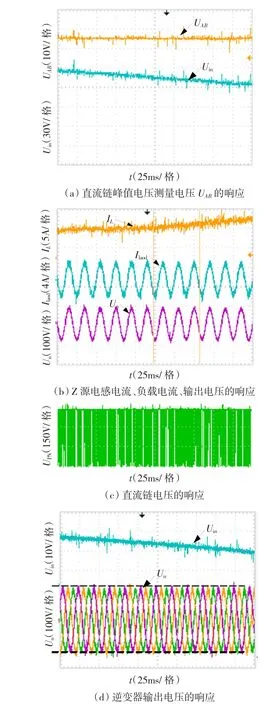
图16 输入电压跌落时的实验结果Fig.16 Experimental results subjected to input voltage sudden sag change

图17 负载变化时的实验结果Fig.17 Experimental results subject to load step change

6 结语

与传统Z源逆变器相比，增强型Z源逆变器具有升压能力强、Z源网络电容电压应力小的优点。本文针对原有采用电容电压反馈间接控制直流链电压这种方式所存在的控制精度不高、动态响应慢的缺点，提出了利用直流链峰值电压控制直流链电压的方法，利用利用电容电压和输入电压预估直流链峰值电压，根据建模获得的直流链峰值电压的小信号模型，设计了Z源电感电流为内环和直流链峰值电压为外环的双闭环控制器，提高了系统的控制精度和动态响应速度，能够抑制输入和负载的扰动对直流链电压的影响。仿真和实验结果证明了控制策略的有效性。

［1］ PENG Fangzheng.Z-source inverter［J］.IEEE Transactions on Industry Applications，2003，39(2):504 －510.

［2］ 彭方正，房绪鹏，顾斌，等.Z源变换器［J］.电工技术学报，2004，19(2):47－51.

PENG Fangzheng，FANG Xupeng，GU Bin，et al.Z-Source converter［J］.Transactions of China Electrotechnical Society，2004，19(2):47－51.

［3］ ZHU Miao，YU K，LUO Fanglin.Switched inductor Z-source inverter［J］.IEEE Transactions on Power Electronics，2010，25(8):2150－2158.

［4］ TANG Yu，XIE Shaojun，ZHANG Chaohua，et al.improved Z-source inverter with reduced Z-source capacitor voltage stress and soft-start capability［J］.IEEE Transactions on Power Electronics，2009，24(2):409－415.

［5］ GAJANAYAKE C J，LUO F L，GOOI H B，et al.Extended Boost Z-source inverters［J］.IEEE Transactions on Power Electronics，2010，25(10):2642 －2652.

［6］ 蔡春伟，曲延滨，刘芳，等.一种高增益 Z源逆变器:中国，201110166524.4［P］.2011－10－19.

［7］ LIN Jinbo，HU Jianggang，XU Longya.Dynamic modeling and analysis of Z Source converter-derivation of AC small signal model and design-oriented analysis［J］.IEEE Transactions on Power E-lectronics，2007，22(5):1786 －1786.

［8］ LOH P C，VILATHGAMUA D M，GAJANAYAKE C J，et al.Transient modeling and analysis of pulse-width modulated Z-source inverter［J］.IEEE Transactions on Power Electronics，2007，22(2):498－507.

［9］ TRAN Q V，CHUN T W，AHN J R，et al.Algorithms for controlling both the DC Boost and AC output voltage of the z-source inverter［J］.IEEE Transactions on Industry Electronics，2007，54(5):2745－2750.

［10］ DING Xinping，QIAN Zhaoming，YANG Shuitao，et al.A direct peak DC-link Boost voltage control strategy in Z-source inverter［C］//Twenty Second Annual IEEE Applied Power Electronics Conference，February 25 － March 1，2007，Anaheim，USA.2007:648－653.

［11］ 丁新平，钱照明，崔彬，等.基于模糊PID的Z源逆变器直流链升压电路控制［J］.中国电机工程学报，2008，28(24):31－38.

DING Xinping，QIAN Zhaoming，CUI Bin，et al.Fuzzy PID controller for DC-link Boost voltage in Z-source inverter［J］.Proceedings of the CSEE，2008，28(24):31－38.

［12］ GAJANAYAK C J，VILATHGAMUWA D M，LON P C.Development of a comprehensive model and a multiloop controller for Z-source inverter DG systems［J］.IEEE Transactions on Power E-lectronic，2007，44(4):2352 －2359.

［13］ TANG Yu.A new direct peak DC-link voltage control strategy of Z-source inverters［C］//2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition，February 21－25，2010，Palm Springs，USA.2010:867 －872.

［14］ 程如岐，赵庚申，郭天勇.Z源逆变器的状态反馈控制策略［J］.电机与控制学报，2009，13(5):673 －678.

CHENG Ruqi，ZHAO Gengshen，GUO Tianyong.State feedback control strategy of Z-source inverter［J］.Electric Machines and Control，2009，13(5):673 －678.

［15］ SEN G，ELBULUK M E.Voltage and current-programmed modes in control of the Z-source converter［J］.IEEE Transactions on Industry Applications，2010，46(2):680 －686.