低温下自旋为1/2的X-Y亚铁磁棱型链的元激发谱

成泰民， 王蕴鹏

(沈阳化工大学数理系，辽宁沈阳110142)

低维磁性系统存在许多奇异的特性，因此，这一领域的研究引起了科学家们广泛的兴趣［1-7］. 1997年日本的Shiomi［1］等人通过实验合成了自旋为 1/2交替的亚铁磁性复合物.2005年Kikuchi［2］等人通过实验发现Cu3(CO3)2(OH)2材料的磁化强度在低温下随外磁场的变化呈现1/3的磁化平台，在低温区磁化率随温度变化出现双峰等特性，并提出自旋1/2的阻挫棱型链模型.有机分子磁性的特点是分子内部自旋-自旋的相互作用具有多通道和多触点，而且，一般在晶态时，一个自旋1/2有机分子内的相互作用强度在数量级上几乎相同.

范洪义的论文［8-9］较详细地介绍了不变本征算符法应用.因为体系的任意幺正变换联系着同一个量子体系的不同表象之间的变换，所以，蕴含着该量子体系严格一致的物理内容，这些幺正变换对该量子体系的描述是完全等价的.因此，在磁性物理及量子力学中普遍采用不同的幺正变换处理系统哈密顿量的对角化，求出元激发能量及基态能量.但是，这一方法的关键是做出适合体系对角化的不同的幺正变换，利用幺正变换处理体系哈密顿量的过程比较繁琐［10-11］.封闭链的格林函数的运动方程法［4-5，11］(切断近似法)也能够处理体系元激发能量.本文利用不变本征算符(invariant eigen-operator，简称IEO)法处理线性近似下的Hamiltonian量体系的元激发能量，该方法比上述两种方法简捷.系统的元激发谱计算是研究系统的自由能、内能、比热、磁化强度、磁化率等的前提.

1 系统的Hamiltonian及元激发谱

双自由基分子和单自由基分子交替排列构成的自旋为1/2的一维亚铁磁棱型链［1-5］如图1所示，其中S2，l和S3，l表示双自由基分子的量子自由基，S1，l表示单自由基分子的量子自由基.J0(＜0)表示双自由基分子内的铁磁相互作用，J＞0表示双自由基分子与单自由基分子间的反铁磁相互作用，并且假设这样的循环结构具有N个(l=1，2，…，N).

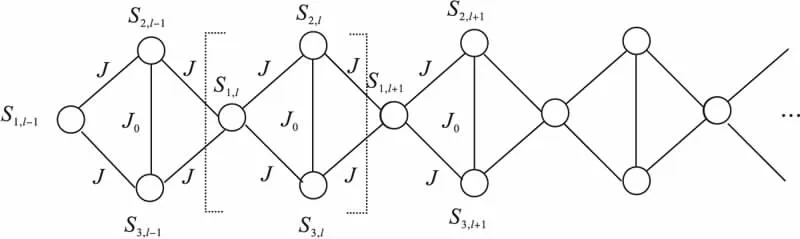
图1 双自由基分子和单自由基分子交替排列构成的自旋为1/2的一维亚铁磁棱型链系统模型Fig.1 The system model of a spin-1/2 one-dimensional ferrimagnetic diamond-like chain consist of biradical molecules and single radicals molecules arrangement alternately

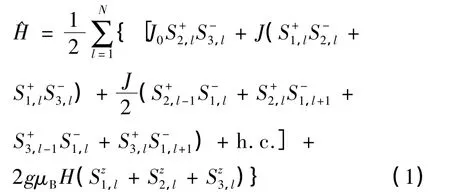
式(1)中，Si，l是自旋1/2的量子算符，S2，l和S3，l由分子内的铁磁相互作用J0＜0耦合连接，其他作用都由表示分子之间的反铁磁相互作用J＞0耦合连接，μB为玻尔磁子，g为朗德因子，H表示外磁场强度.

对式(1)自旋升降算符进行 Jordan-Wigner (J-W)变换［4－7，12］:

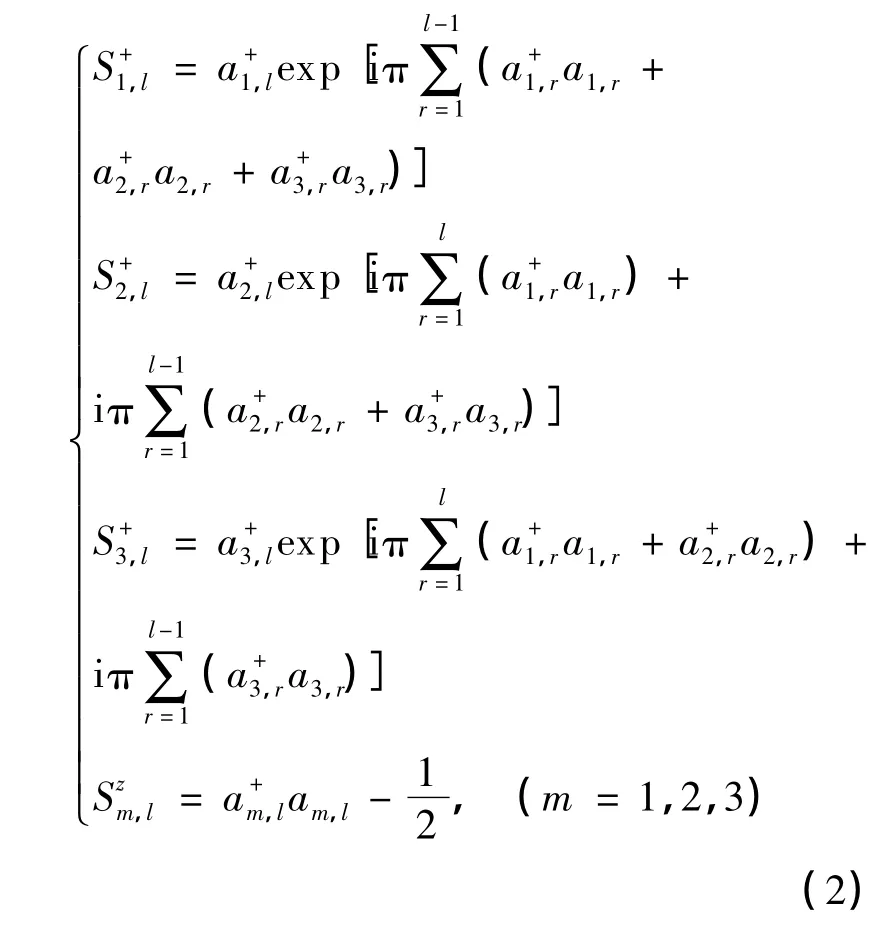
由式(2)可得:

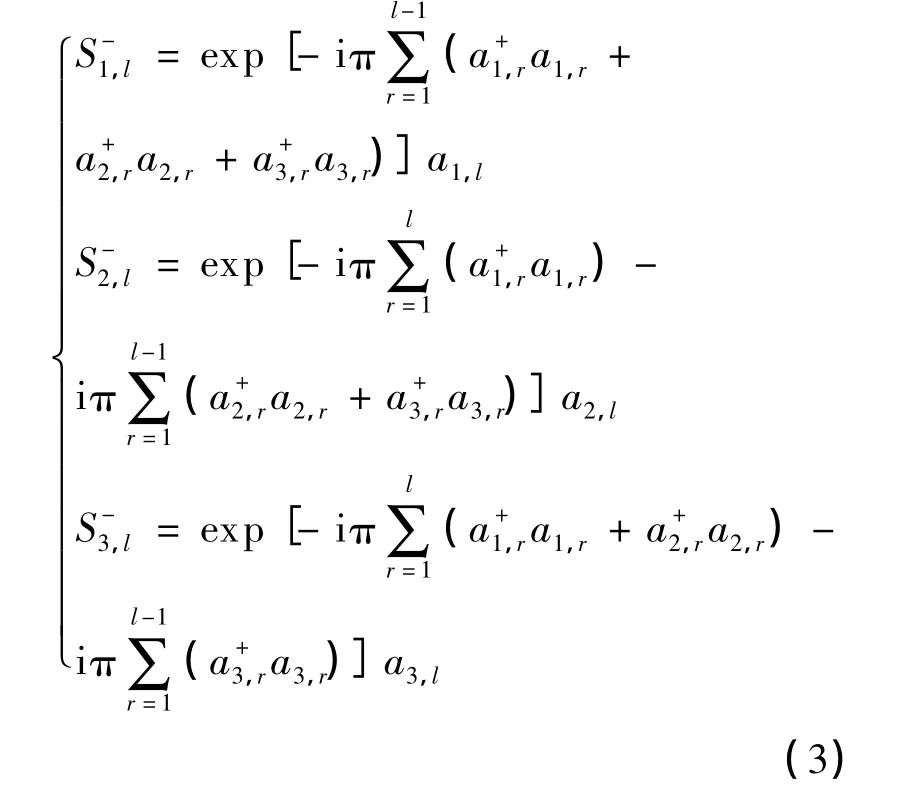
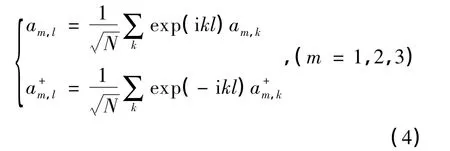
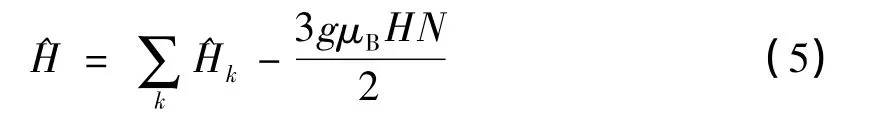
其中

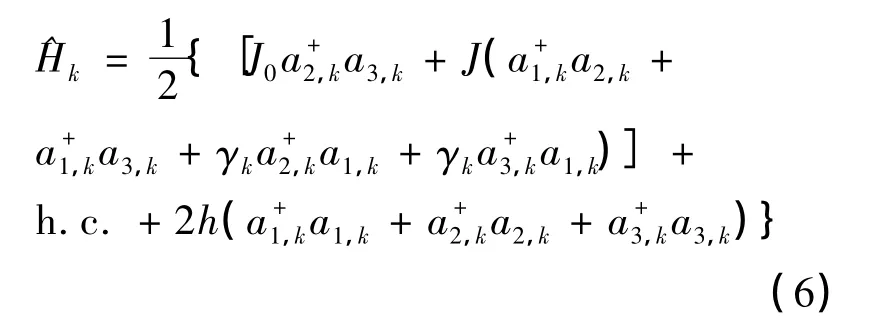
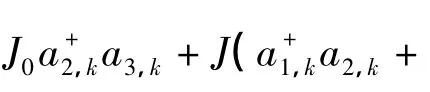
相对于系统的Hamiltonian^H，关于算符ai，k，(i =1，2，3)的IEO为 ^Oe，σ，并令

其中

式(8)可以表示为:

其中τ1，σ，τ2，σ，τ3，σ是复数.

根据式(7)～(11)可得:

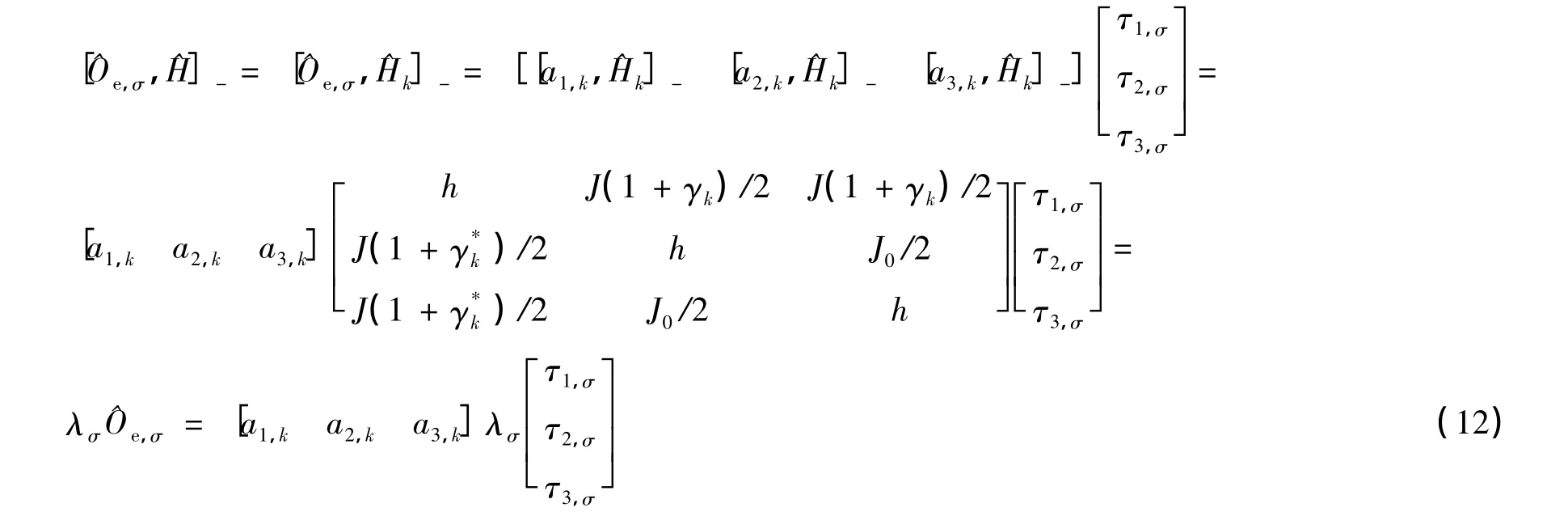
令

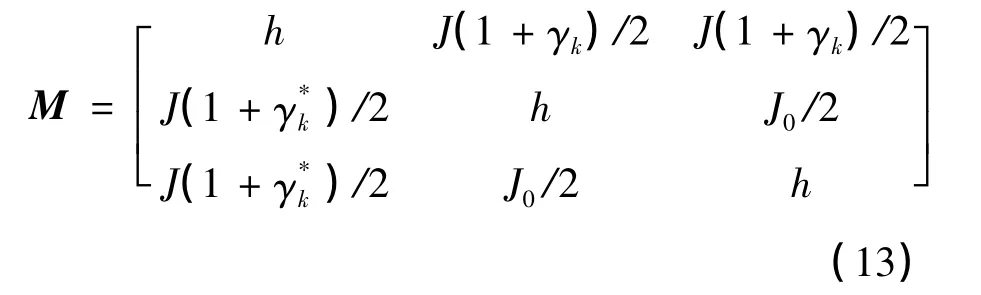
从而得:

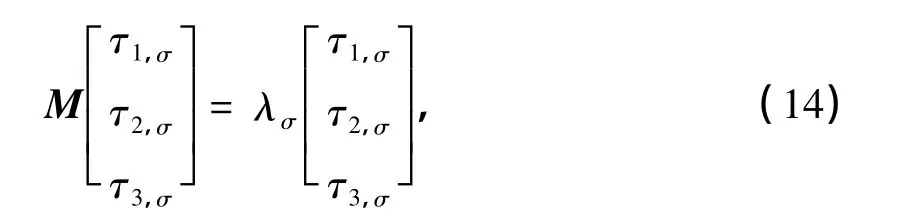
求解式(14)的久期方程［13］，可得自旋为1/2一维亚铁磁棱型链系统的元激发能量:

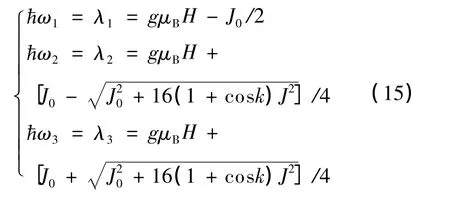
式(15)与文献［1，5］的模型相对应.式(12)比文献［5］的结果更加明晰.

因为本文利用IEO法处理磁有序系统时，没有直接涉及到某两个特定的不同定态，而是直接通过本征算符与其对应的Heisenberg方程计算，与体系相邻能级能量差的大小相对应，所以，这就是体系的能量量子化的量子.

因为矩阵M是厄米矩阵，且λ1≠λ2≠λ3，所以，对应的本征态之间相互正交，其本征态如下:

根据式(6)、(9)、(10)、(15)、(16)可得:

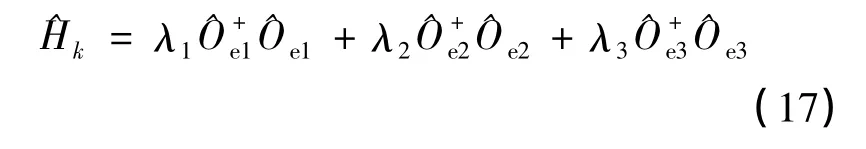
式(17)是退耦后的Hamiltonian^Hk，其中不变本征算符^O+eσ、^Oeσ也满足费米-狄拉克反对易关系.

2 讨论

利用IEO法计算磁有序系统的线性近似下的Hamiltonian所对应的元激发能量非常方便，但是IEO法不易直接给出磁有序系统的基态能量，并且利用IEO法几乎无法处理含有算符的三次项或者更高次项的Hamiltonian量体系(如电子-声子耦合体系，磁振子-声子耦合体系，声子-声子耦合体系，磁振子-磁振子耦合体系等)，在这一点IEO法不如格林函数理论及量子场论的费曼图技术.

IEO法对于Hamiltonian的退耦合处理上比幺正变换处理更加便捷，而且直接在系统的能量自表象上自动退耦，因此，这对计算系统的配分函数而言非常便捷.这一工作是自旋为1/2的一维X-Y模型亚铁磁棱型链系统热学性质与磁性质研究的至关重要的前提.

［1］ Shiomi D，Nishizawa M，Sato K，et al.A Prerequisite for Purely Organic Molecule-based Ferrimagnetics: Breakdown of Simple Classical Pictures［J］.J.Phys. Chem.B，1997，101(17):3342-3348.

［2］ Kikuchi H，Fujii Y，Chiba M，et al. Experimental Observation of the 1/3 Magnetization Plateau in the Diamond-chain Compound Cu3(CO3)2(OH)2［J］. Phys.Rev.Lett.，2005，94(22):227201.

［3］ Maekawa K，Shiomi D，Ise T，et al. Theoretical Study on Spin Alignments in Ferromagnetic Heterospin Chains with Competing Exchange Interactions: A Generalized Ferrimagnetic System Containing Organic Biradicals in the Singlet Ground State［J］.J. Phys.Chem.B，2005，109(19):9299-9304.

［4］ Fu H H，Yao K L，Liu Z L.Thermodynamic Properties of a Spin-1/2 Diamond Chain as a Model for a Molecule-based Ferrimagnetand theCompound Cu3(CO3)2(OH)2［J］.Phys.Rev.B，2006，73 (10):104454.

［5］ Fu H H，Yao K L，Liu Z L.Specific Heat Study on a Spin-one-half Frustrated Diamond Chain［J］.Phys. Lett.A，2006，358(5/6):443-447.

［6］ 李嘉亮，类淑国.具有长程相互作用的S-1/2XY链的研究［J］.物理学报，2008，57(9):5944-5950.

［7］ 高阳，张豫梅，陈鸿.磁场对一维Heisenberg链低能行为的影响［J］.物理学报，2000，49(8):1586-1590.

［8］ Fan Hong Yi，Li Chao.Invariant‘Eigen-operator’of the Square of Schrödinger Operator for Deriving Energy-level Gap［J］.Phys.Lett.A，2004，321(2): 75-78.

［9］ Fan Hong Yi，Wu Hao.Deriving Vibrating Modes of Some Multiatom Molecules by Virtue of the Invariant Eigenoperator Method［J］.Modern Physics Letters B，2005，19(26):1361-1366.

［10］柳盛典，逯怀新，邓汝刚.幺正变换与二粒子耦合体系哈密顿量的对角化技术［J］.大学物理，1993，12(5):25-26.

［11］蔡建华，龚昌德，姚希贤，等.量子统计的格林函数理论［M］.北京:科学出版社，1982:18-23，195-227.

［12］Batista C D，Ortiz G. Generalized Jordan-wigner Transformations［J］.Phys.Rev.Lett.，2001，81(6): 1082-1085.

［13］王竹溪，郭敦仁.特殊函数概论［M］.北京:北京大学出版社，2000:645-649.