数形结合剖析水波的干涉图样

陈 敏

(慈溪市浒山中学 浙江 宁波 315300)

“波的干涉”一节的教学难点在于对稳定而动态的波的干涉图样的理解.稳定性是指空间内每个质点的振动强弱是固定的，动态性则是指每个质点的位移又是时刻变化的.学生感觉比较难以把握的是，稳定和动态的特征表现在干涉图样上是怎样的？画面动态有序的背后隐含质点遵循着怎样的规律？通过数形结合的方法来突破上述难点可以取得较为理想的效果.数形结合把直观的图形表达方式与抽象的数学表达方式相结合来解决问题，一方面借助数学的精确性和严密性对图形做精细的分析，从而对图形有更深刻的认识；另一方面用图像形象地体现数学的抽象表达，有助于对复杂数学公式的理解，达到理解水波干涉图样的目标，分析如下.

图1

根据波的叠加原理，实际振动的运动学方程为

令

则

y=A合cos(ωt+φ0)

式中A合和φ0分别为两分振动在P点的合振幅和初相位.可见质点是做角频率依然为ω的简谐运动，其振动特征与空间位置和时间变化相关.下面从空间、时间来分析波的干涉图样的稳定性和动态性.

1 空间位置决定振幅和初相体现稳定性

图2

即r1+r2=d+2kλ，质点与S1，S2连线间的质点相差为零，振动步调一致，如图3实线椭圆.

r1+r2=d+(2k-1)λ

质点与S1，S2连线间的质点振动步调相反，如图3虚线椭圆.

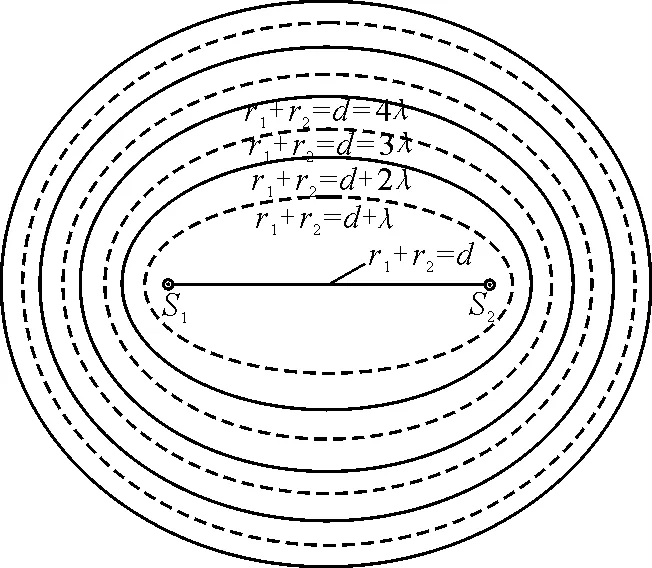
图3

在单一波源形成波的传播过程中，每个质点都重复波源的振动形式，相同相位的质点形成的波面是以波源为圆心的一系列同心圆，波面沿半径方向向外扩散；与此相似，质点在两个波源的带动下产生的振动也将从S1，S2连线沿着双曲线(在S1，S2连线方向上沿连线方向)向外传播形成越来越大的“同焦”椭圆形的波面，此处的双曲线和椭圆可类比成波线和波面，如图4所示.

图4

2 时间决定质点的位移体现动态性

由于有两个波源使得质点的振动形式较单一波源作用时有更丰富的形式，下面详细分析两个波源S1，S2之间的质点的振动，其他质点都可以看作是重复着这些质点的振动形式.

S1，S2连线上的质点的振动方程均可表示成

若连线间距为2λ，由

可知，连线的中点A0满足|r2-r1|=0，是加强点，称作零级加强区；A1左，A1右满足|r2-r1|=λ,称1级加强区；A2左，A2右满足|r2-r1|=2λ，称2级加强区.A0，A2左，A2右的振动方程为

A1左，A1右振动方程为

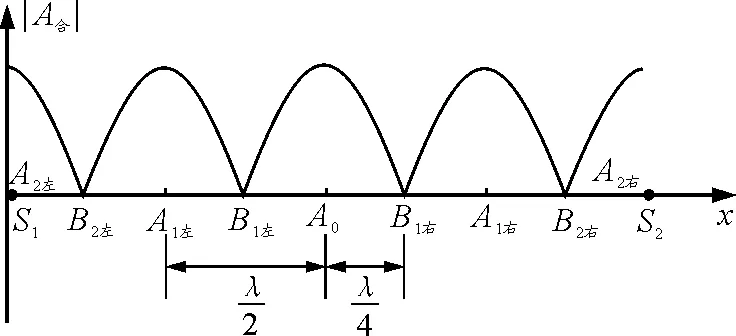
图5

现在用图6来说明S1，S2连线上的质点一个周期内所表现出来的波形.图中可以看到，所有质点在同一时刻到达最大位移，同一时刻经过平衡位置，同一时刻到达最小位移，波形图并不沿着S1，S2连线方向移动，只看到波形上下起伏.这种由振幅相同传播方向相反的两列简谐相干波叠加得到的振动称为驻波，相邻加强区的正负最大位移间隔出现，加强点的起伏最大，形成波腹，减弱点不发生振动，形成波节.驻波不是波而是一种特殊的振动状态，波源S1，S2连线上质点的振动形式没有沿着连线传播，却沿着双曲线向外传播，看起来连线间的振动形式从S1，S2连线出发沿着双曲线两侧传播，单一波源形成的波面是一圈圈的同心圆，在水面上看到圆形的涟漪，这里形成的是一圈圈椭圆状的“波面”，水面上呈现出椭圆状的涟漪；而且，椭圆上也形成类似的“驻波”，此“驻波”也并不沿着椭圆方向传播，而是继续沿着双曲线荡成更大的椭圆状的涟漪.

图6

图7

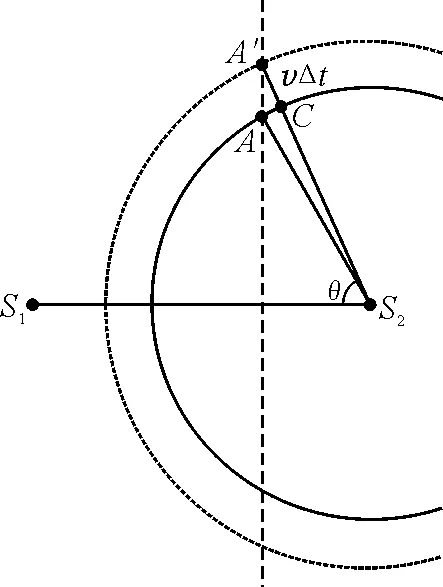
图8

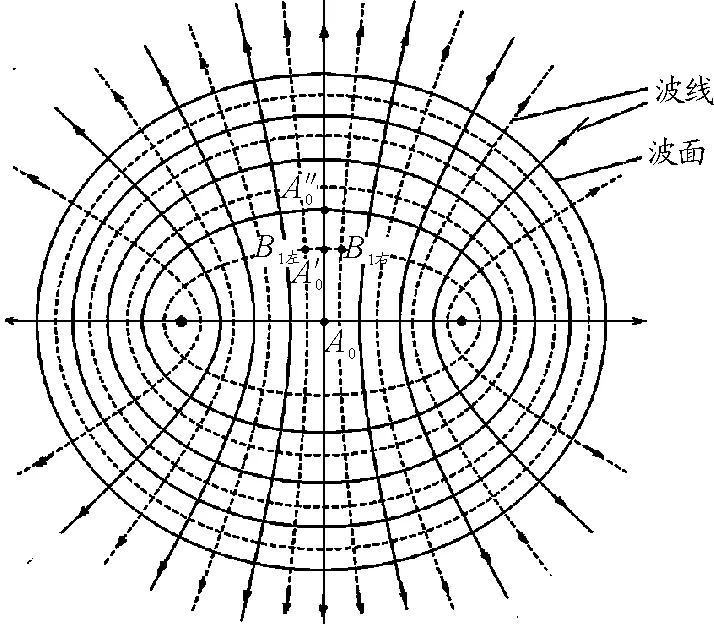
图9

每一个质点的振动形式是简单的，但是空间的分布和时间的变化使得整个图样错落有序，变化多端，就像一场大型的团体操表演中，每一个演员的动作并不复杂，但众多演员的参与，前后左右相邻演员的动作错落有致，就形成了气势恢宏，蔚为壮观的艺术画卷.在干涉现象中，每一个质点严格恪守着运动规律，就像是一个个优秀的演员在高度的组织协调下表演，演绎成一幅整齐生动的干涉画面.