Logistic回归模型及其应用

常振海，刘薇

（天水师范学院 数学与统计学院，甘肃 天水741001）

Logistic回归模型及其应用

常振海，刘薇

（天水师范学院 数学与统计学院，甘肃 天水741001）

为了利用Logistic模型提高多分类定性因变量的预测准确率，在二分类Logistic回归模型的基础上，对实际统计数据建立三类别的Logistic模型.采用似然比检验法对自变量的显著性进行检验，剔除了不显著的变量；对每个类别的因变量都确定了1个线性回归函数，并进行了模型检验.分析结果表明，在处理因变量为定性变量的回归分析中，Logistic模型具有很好的预测准确度和实用推广性.

定性变量；Logistic回归模型；预测

Logistic回归属于概率型非线性回归，是分析因变量为定性变量的常用统计分析方法.由于Logistic回归模型对数据的正态性、方差齐性以及自变量类型不做要求，并且具有系数的可解释性等优点，使得其在医学、社会学、经济学等领域得到了广泛的应用［1－4］.目前，对Logistic回归模型的研究已取得很多好的结果［5－6］，但这些结果多侧重于二分类Logistic回归模型.本文在二分类Logistic回归模型的基础上，以实例为背景讨论了较为复杂的多分类Logistic回归模型.

1 Logistic模型概述

通常意义上的Logistic回归要求因变量y只有2种取值（二分类），但当y的取值有2种以上时，就要用多分类Logistic回归分析（Multinomial Logistic Regression）.

1.1 二分类Logistic回归分析

1）模型及其背景.在许多情形下，Logistic回归的因变量是二分类的.下面考虑一般的多元回归模型i（1－πi）1－yi，yi＝0，1.显然有E（yi）＝πi＝f（xi1，xi2，…，xip），故当因变量为0－1型随机变量时，因变量均值表示给定自变量时y＝1的概率.又因为0≤E（yi）＝πi≤1，所以因变量均值受到限制.另外，误差项εi＝yi－f（xi1，xi2，…，xip）为具有异方差性的两点型离散分布.事实上，Var（εi）＝Var（yi）＝πi（1－πi）＝f（xi1，xi2，…，xip）［1－f（xi1，xi2，…，xip）］，εi的方差依赖于xi＝ （xi1，xi2，…，xip），且具有异方差性，这时当yi＝1时，εi＝yi－f（xi1，xi2，…，xip）＝1－πi；当yi＝0时，εi＝yi－f（xi1，xi2，…，xip）＝－πi.

其中：εi满足E（εi）＝0；yi为0－1型随机变量，其概率分布为P（yi）＝πyi

针对0－1型因变量产生的问题，对回归模型做2个方面的改进：首先，回归函数改用限制在［0，1］区间内的连续曲线g（x）.限制在［0，1］区间内的连续曲线有很多，如所有连续型随机变量的分布函数都符合要求，其中常用的是Logistic函数.其次，因变量yi本身只取0和1两个离散值，不适合于直接作为回归模型中的因变量.由于回归函数E（yi）＝πi＝f（xi1，xi2，…，xip）表示在自变量为xi1，xi2，…，xip的条件下yi等于1的比例，所以可以用yi等于1的概率代替yi本身作为因变量.于是得到了Logistic回归方程：

2）参数形式的Logistic回归.若式（1）中的f（·）为多元线性函数，则上述模型可写成

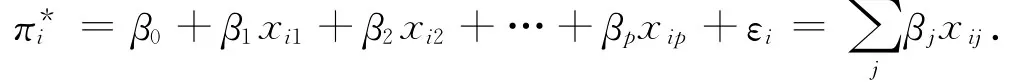
模型的参数估计分2种情形：①在大样本下，常把数据分成若干组，比如c组，每组的个数为ni，i＝因为异方差性的存在，一般采用加权最小二乘法来估计其中的参数.又因πi＝E（yi），故可以选择权函数为ωi＝nipi（1－pi）.因该算法和普通最小二乘估计十分相近，故省略具体的算法过程.当ni较大时，π＊i的近似方差为其证明参见文献［7］.② 在小样本下，可以把yi的概率函数合写为P（yi）＝πyii（1－πi）1－yi，其中yi＝0，1；i＝1，2，…，n.于是，y1，y2，…，yn的似然函数为，取自然对数可得

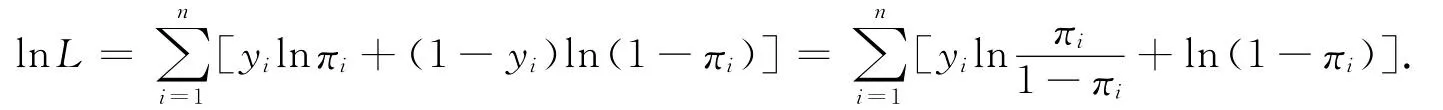
对于Logistic回归，得到

采用极大似然估计方法估计式（4）中参数β＝（β0，β1，…，βp）T，但此时无法用封闭形式找到此估计，故通常采用迭代方法，即选择初始值＝（,，…,）T，i＝1，2，…，n，利用方程（3）计算πi，把βj用估计的代替，经过迭代至收敛，其具体步骤为：①设令β的新估计为＝（XTW X）－1XTWZ，其中W 为对角矩阵，其第（i，j）个元素等于πi（1－πi），即相当于做Z在X上的1个加权线性回归；③以目前的＾β，利用方程（3）计算πi.

1.2 多类别Logistic回归分析

记yj（j＝1，2，…，k）为定性因变量y取的k个类别，πj为y取第j个类别的概率.因变量y取值于每个类别的概率与1组自变量x1，x2，…，xp有关.对于样本数据（xi1，xi2，…，xip），i＝1，2，…，n，多类别Logistic回归模型第i组样本的因变量yi取第j个类别的概率为

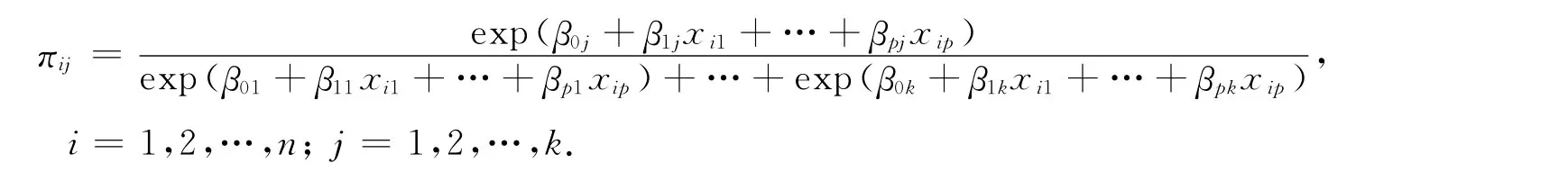
上式中各回归系数不是唯一确定的，每个回归系数同时加减1个常数后的数值保持不变.为此，把分母的第一项中的系数都可设为0，称为参照系数，其他类别回归系数值的大小都以系数设为0的类别的回归系数为参照，于是得到回归函数的表达式：

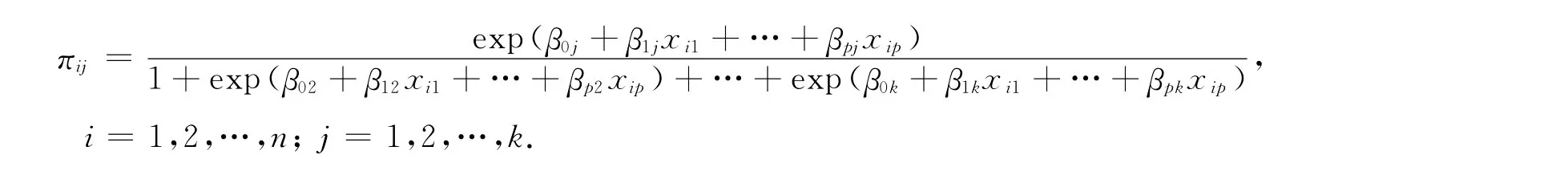
2 实例分析

实例数据资料来源于软件SPSS 13.0的自带数据.某快餐公司让随机抽选的880名顾客品尝了公司的3种早餐套餐：y1－Breakfast Bar，y2－Oatmeal，y3－Cereal.然后让每位顾客选定自己最喜欢的套餐，并记录下顾客的年龄、性别、婚姻情况和健身运动情况（1周至少2次）.以Preferred breakfast为因变量（用bfast简记为相应变量名称，下同，并用“－”连接），以定性变量age category－agecat，gender－gender，marital status－marital，active lifestyle－active为自变量做统计分析，结果见表1（利用SPSS软件运算）.

表1给出了分类变量各类别的频数和频率，其中频率仅是从数据直接做出的统计结果.下面采用多类别的Logistic模型做比较分析.首先采用似然比检验法进行自变量显著性检验，其中对定性变量的检验是整体检验，结果见表2.由表2可知变量gender不显著，说明在该调查中性别对套餐的影响可以忽略，故剔除后再做检验，结果见表3.

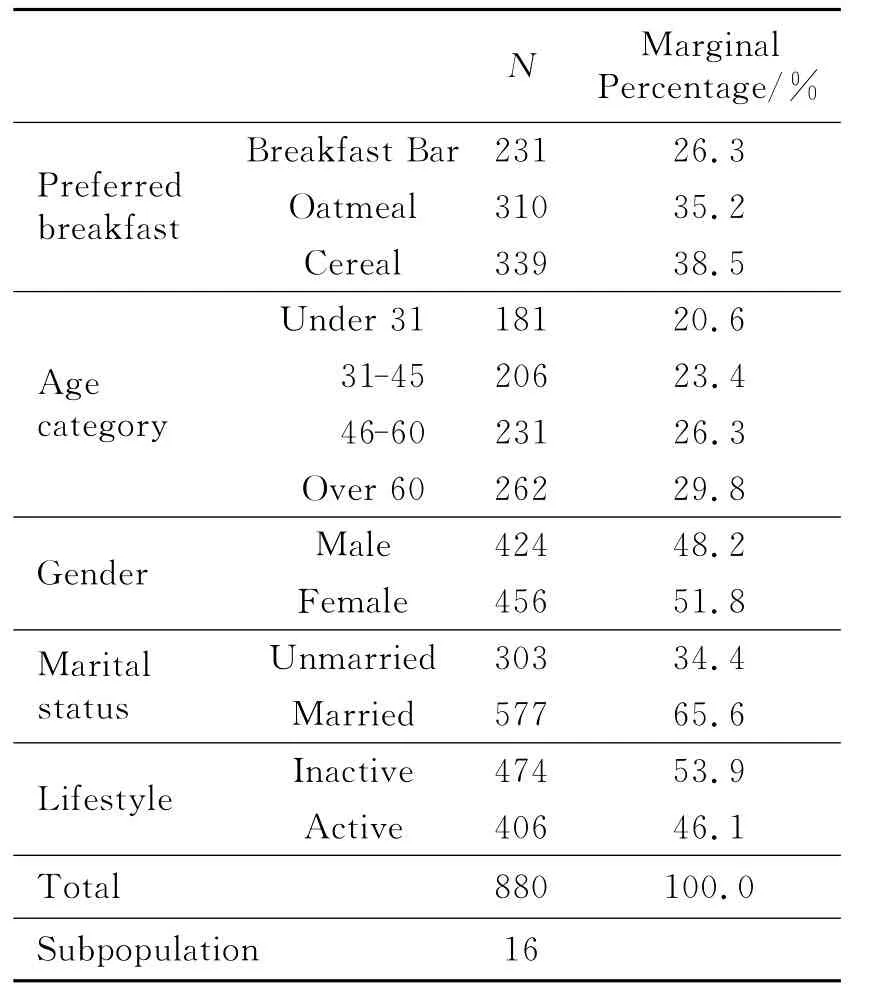
表1 变量总结

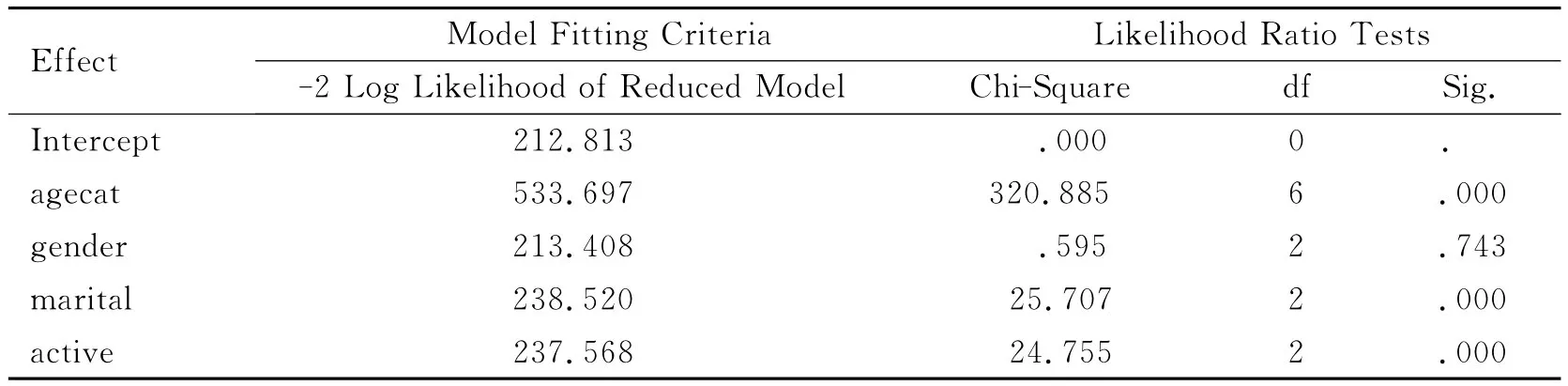
表2 似然比检验结果

表3 似然比检验结果

表3显示各变量均显著.本例因变量共有3个类别：1－Breakfast Bar，2－Oatmeal，3－Cereal，其中第1个类别作为基准，回归系数取为0.对于第2和第3类别，每个类别都需要确定1个线性回归函数，因此每个自变量都有2个回归系数，自由度为2.每1个定性自变量要用其类别数减去1个示性变量表示，如Age category共有4个变量取值，要用3个示性变量表示，因此有2×3＝6个回归系数，把Age category作为1个整体时的自由度为6.从表3中可以看出，自变量agecat的相伴概率为Sig.＝0.000，说明该变量作为1个整体检验是显著的；但整体显著并不表示该自变量的每个取值都显著，如在表4的参数估计结果中，对因变量的类别2（Oatmeal），当agecat＝3时Sig.＝0.177，所以其就不显著，其余可类似参阅.

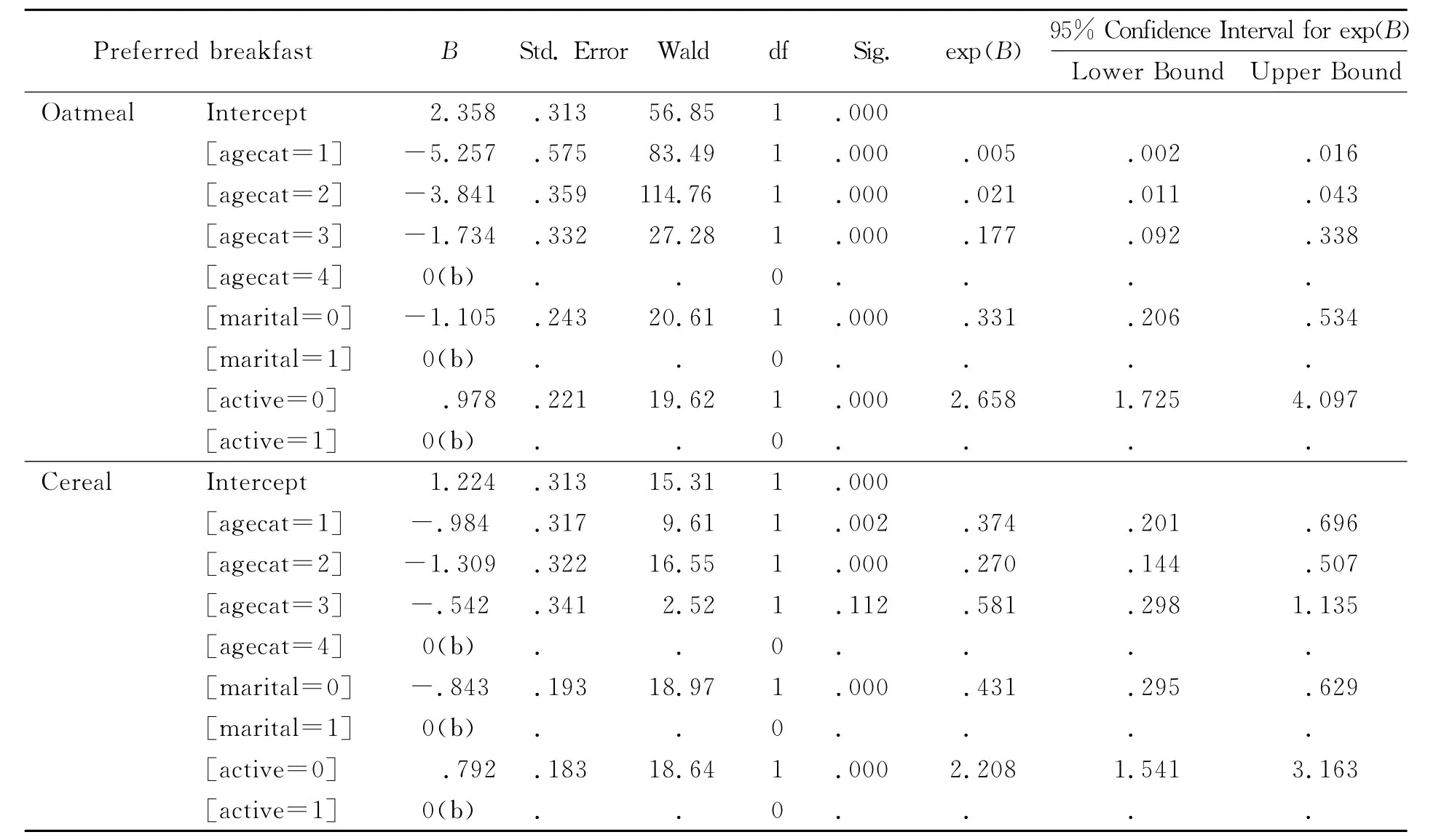
表4 参数估计

尽管从整体上对变量和其各个类别做了探讨，但为确定该组数据拟合Logistic回归模型是否合适，需要进行有效性检验，其结果见表5.其中原假设是回归模型无效，所有系数均为0.

表5 模型的拟合优度信息

模型检验表明回归模型显著有效，可用于预测.对每个样品计算出因变量y取第j个类别的概率πj，因变量的预测值是πj最大的类别，结果见表6.

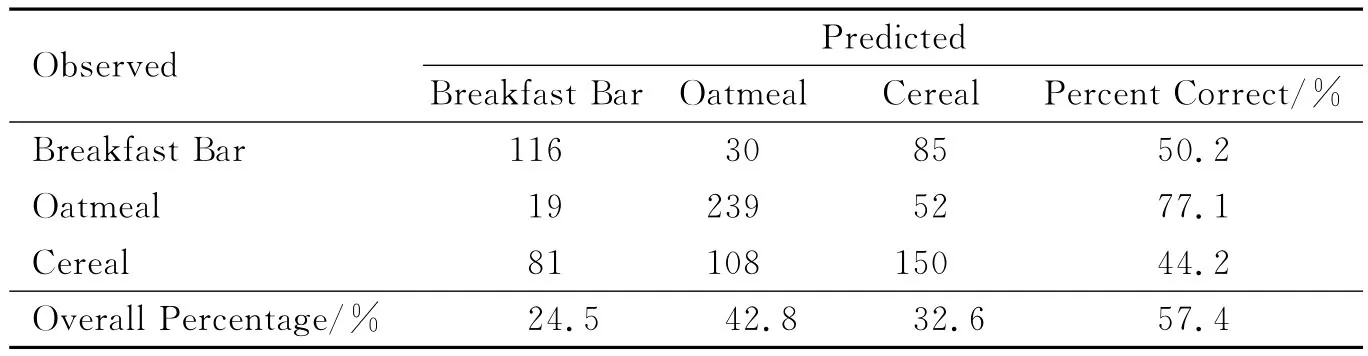
表6 预测结果

表6显示：Breakfast Bar类别的231个观测值中，有116个预测正确，正确率为50.2%；Oatmeal类别的310个观测值中，有239个预测正确，正确率为77.1%；Cereal类别的339个观测值中，有150个预测正确，正确率为44.2%；在全部880个观测值中，有505个预测正确，总正确率为57.4%.

3 结论

从以上的分析可以分别得出对因变量y的3个类别（y1－Breakfast Bar，y2－Oatmeal，y3－Cereal）的预测概率的提高情况：①若没有任何信息资料，全凭猜测，可能有4种情形，分别为y1，y2，y3或都不是，由随机性知每个类别的预测概率均为25%，预测总正确率为25%；②若据现有数据信息，做一般的频数频率统计（表1），因变量3个类别y1，y2，y3的频率分别为26.3%、35.2%和38.5%，与情况①相比，预测的正确率分别提高1.3%、10.2%和13.5%；③通过回归分析，y1，y2，y3的预测正确率能在情况②的基础上分别提高23.9%、41.9%和5.7%（表6）.因变量y的3个类别中，第2个类别（Oatmeal）的预测效果最好，正确率为77.1%；第3个类别（Cereal）的预测效果最差，正确率仅为44.2%，说明现有数据不能很好地解释该类变量，若想进一步提高预测率，需要对该类别的客户群做进一步的研究，以便找出相关的解释变量.但总的来说，在处理因变量为定性变量的回归分析中，Logistic模型具有很好的预测准确度和实用推广性.

［1］王昊.Logistics回归模型在广东省房价预测中的应用研究［J］.现代商贸工业，2010（16）：304－306.

［2］袁建林，陈立文，景楠.基于Logistic模型的房地产上市公司经济效益风险评价研究［J］.统计与决策，2010（18）：77－79.

［3］杨茜.基于Logistic回归模型的航运业上市公司投资价值评价［J］.科技创业月刊，2010（8）：99－101.

［4］董晓萌.Logistic回归模型诊断肺癌病人的生存时间［J］.科学技术与工程，2010，10（26）：6519－6521.

［5］何晓群，刘文卿.应用回归分析［M］.北京：中国人民大学出版社，2009：242－266.

［6］李江辉，曹素华.多分类属性反应变量分析方法初探［J］.中国卫生统计，2000，17（5）：287－289.

［7］张尧庭.定性资料的统计分析［M］.桂林：广西师范大学出版社，1991：111－165.

Logistic regression model and its application

CHANG Zhen－hai，LIU Wei
（School ofMathematics andStatistics，TianshuiNormal University，Tianshui741001，China）

To improve the forecasting accuracy of the multinomial qualitative dependent variable by using logistic model，ternary logistic model is established for actual statistical data based on binary logistic regression model.The significance of independent variables is tested by using the likelihood ratio test method to remove the non－significant variable.A linear regression function is determined for each category dependent variable，and the models are tested.The analysis results sho wthat logistic regression model has good predictive accuracy and practical promotional value in handling regression analysis of qualitative dependent variable.

qualitative variable；logistic regression model；prediction

1004－4353（2012）01－0028－05

O212.1

A

2011－12－22

天水师范学院中青年教师科研基金资助项目（TSA1007）

常振海（1979—），男，讲师，研究方向为应用概率统计.