关于6的整数倍的另一神奇特征（续九）

王仲才

（南昌理工学院 江西 南昌 330013）

关于6的整数倍的另一神奇特征（续九）

王仲才

（南昌理工学院 江西 南昌 330013）

本文继文[4]给出的6的整数倍的另一种神奇特征。

6；整数倍；正整数；偶数；奇数；立方；9次方；3的任意正整数次方；作和；作差；作积；间隔；代数和

[引理1] 设m为正整数，则每间隔m个正整数的接连的6个正整数的立方中，前3个取负，后3个取正，它们的代数和是3的整数倍，且代数和各位数之和也是3的整数倍。

证明：设n为正整数，则间隔m个正整数的6个函数是

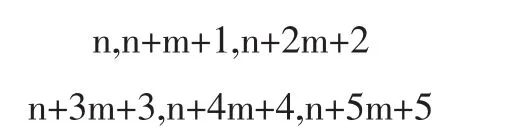
对应项之差都是3m+3=3(m+1)

由两数立方差公式

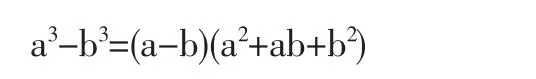
得悉，对应项的立方差中都有公因子3(m+1),从而是3的整数倍，那么它的代数和也是3的整数倍，由文[1]即得后一结论。

[定理1] 设m为正整数，则每间隔m个正整数的6的整数倍正整数的立方中，3的奇数倍取负，3的偶数倍取正，它们的代数和是3的整数倍，且代数和的各位数之和也是3的整数倍。

证明：每6个一组，前3个取负，后3取正，由[引理1]，它们的代数和是3的整数倍，那么总的代数和自然是3的整数倍，由文[1]即得后一结论。

证毕。

[引理2] 设m为正整数，则每间隔m个正整数的接连的6个正整数的9次方中，前3个取负，后3个取正，它们的代数和是3的整数倍，且代数和的各位数之和也是3的整数倍。

证明：前3个是n9,(n+m+1)9,(n+2m+2)9,n为正整数；

后3个是(n+3m+3)9,(n+4m+4)9,(n+5m+5)9

由2数的9次方之差公式

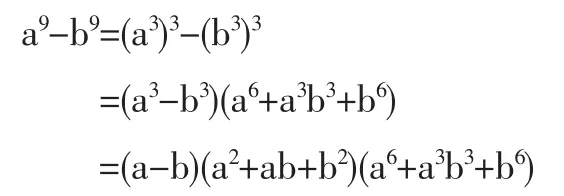
得悉，对应项之差都含3(m+1)的因子，从而是3的整数倍，那么总的代数和自然也是3的整数倍，由文[1]即得后一结论。

证毕。

[定理2] 设m为正整数，则每间隔m个正整数的接连的6的整数倍个正整数的9次方中，3的奇数倍个取负，3的偶数倍取正，它们的代数和是3的整数倍，且其代数和的各位数之和也是3的整数倍。

证明：每6个一组，前3个取负，后3个取正，由[引理2]得悉，它的代数和是3的整数倍，那么总的代数和自然也是3的整数倍，由文[1]即得后一结论。

证毕。

[核心定理3] 设m为正整数，l为正整数，则每间隔m个正整数的接连的6的整数倍个正整数的3l次方中，3的奇数倍个取负，3的偶数倍个取正，它们的代数和是3的整数倍，且代数和的各位数之和也是3的整数倍。

证明：由[定理1]和[定理2]得知,l=1.2对结论成立，假设 l=h（整数)时结论成立，由[定理1]和[定理2]的证明中得知，只要假设对于对应项之差成立即可，即假设

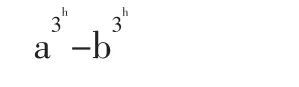
结论成立，那么对于l=h+1，则

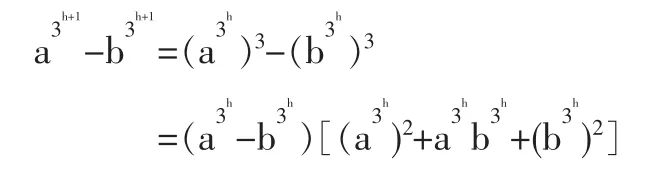
由归纳假设，它是3的整数倍，总的代数和自然是3的整数倍。由文[1]即得后一结论。

证毕。

[推论1] 设m,l为正整数，则每间隔m个正整数的接连的6的整数倍个正整数的3l次方中，3的奇数倍取负，3的偶数倍个取正，它们的代数和与其各位数之和乘以任何有限位数的数之积的各位数之和都是3的整数倍。

证明：这是[核心定理3]和文[1]的直接推论。

证毕。

[引理3] 设m为正整数，则每间隔m个偶数的接连的6个偶数的立方中，前3个取负，后3个取正，它们的代数和是3的整数倍，且其代数和的各位数之和也是3的整数倍。

证明：间隔m个偶数的6个偶数中，前3个是

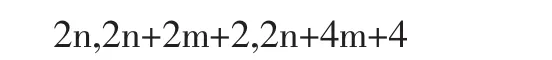
后3个是

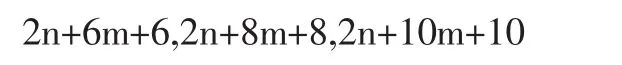
对应项之差都是6m+6=3(2m+2)

由立方差公式

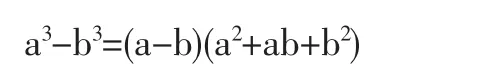
得知，对应项的立方差中都有3(m+2)因子，从而是3的整数倍，那么总的代数和也是3的整数倍，由文[1]即得后一结论。

证毕。

[定理4] 设m为正整数，则每间隔m个偶数的6的正整数倍个偶数的立方中，3的奇数倍取负，3的偶数倍个取正，它们的代数和是3的整数倍，且代数和的各位数之和也是3的整数倍。

证明：每6个一组，前3个取负，后3个取正，由[引理3]得悉，它的代数和是3的整数倍，那么总的代数和自然也是3的整数倍，由文[1]即得后一结论。

证毕。

[引理4] 设m为正整数，则每间隔m个偶数的6个偶数的9次方中，前3个取负，后3个取正，它们的代数和是3的整数倍，其代数和的各位数之和也是3的整数倍。

证明：每间隔m个正偶数的6个偶数是

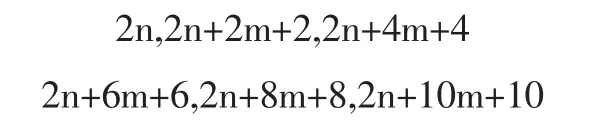
对应项之差都是6m+6=3(2m+2)

由2数9次方之差公式

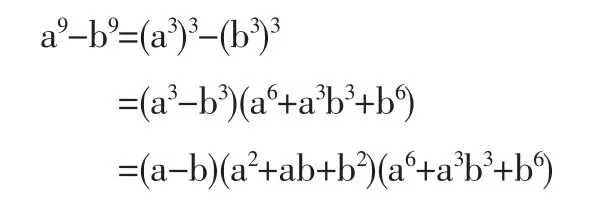
那么，对应项的9次方之差都含3(2m+2)的因子，从而它们的代数和是3的整数倍，总的代数和自然也是3的整数倍，由文[1]即得后一结论。

证毕。

[定理5] 设m为正整数，则每间隔m个偶数的6的整数倍个偶数的9次方中，3的奇数倍个取负，3的偶数倍个取正，它们的代数和是3的整数倍，且代数和的各位数之和也是3的整数倍。

证明：每6个一组，由[引理4]得悉，它们的代数和是3的整数倍，那么总的代数和自然也是3的整数倍，由文[1]即得后一结论。

证毕。

[核心定理6] 设m,l为正整数，则每间隔m个偶数的6的正整数倍个偶数的3l次方中，3的奇数倍个取负，3的偶数倍取正，它们的代数和是3的整数倍，且代数和的各位数之和也是3的整数倍。

证明：由定理[4]、[5]得知 l=1,2，结论成立。

现在假设l=h（整数）时结论成立。由[定理4]与[定理5]的证明中得知，只要假设l=h，对于对应项结论成立即可，亦

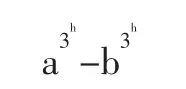
结论成立，那么对于l=h+1

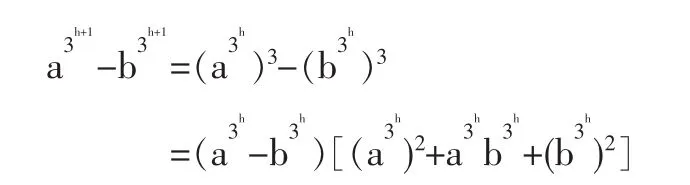
由假设，结论也成立，由文[1]即得后一结论。

证毕。

[推论2] 设m,l为正整数，则每间隔m个偶数的6的整数倍个偶数的3l次方中，3的奇数倍取负，3的偶数倍取正，它们的代数和与其各位数之和乘以任何有限位数的数之积的各位数之和都是3的整数倍。

证明：这是[核心定理6]与文[1]的直接推论。

证毕。

[引理5] 设m为正整数，则每间隔m个奇数的6个奇数的立方中，前3个取负，后3个取正，它们的代数和是3的整数倍，且代数和的各位数之和也是3的整数倍。

证明：设n为正整数，则每间隔m个奇数的6个奇数中前3个是

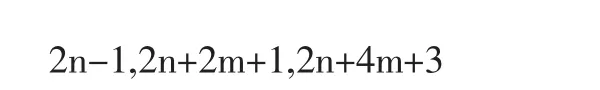
后3个是

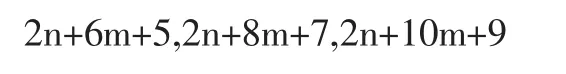
对应项之差是6m+6=3(2m+2)

由2数立方差公式

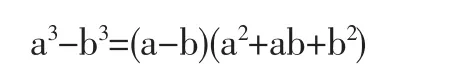
得悉对应项的立方差均含有因子3(2m+2),从而是3的整数倍,那么总的代数和自然是3的整数倍,由文[1]即得后一结论。

[定理7]设m为正整数，则每间隔m个奇数的6的整数倍个奇数的立方中，3的奇数倍个取负，3的偶数取正，它们的代数和是3的整数倍，且代数和的各位数之和也是3的整数倍。

证明：每6个一组，前3个取负，后3个取正，由[引理5]得悉，它的代数和是3的整数倍，那么总的代数和自然是3的整数倍，由文[1]即得后一结论。

[引理6]设m为正整数，则每间隔m个奇数的6个奇数的9次方中，前3个取负，后3个取正，它们的代数和是3的整数倍，且代数和的各位数之和也是3的整数倍。

证明：如[引理5]和二数9次方差公式

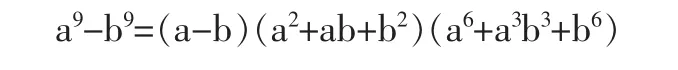
得知，对应项之差均含有因子3（2m+2），从而是3的整数倍，那么总的代数和自然是3的整数倍，由文[1]即得后一结论。

[定理8]设m为正整数，则每间隔m个奇数的6的整数倍个奇数的9次方中，3的奇数倍取负，3的偶数倍个取正，它们的代数和是3的整数倍，且代数和的各位数之和也是3的整数倍。

证明：每6个一组，前3个取负，后3个取正，由[引理6]得悉，它的代数和是3的整数倍，那么总的代数和自然是3的整数倍，由文[1]即得后一结论。

[核心定理9]设m、l为正整数，则每间隔m个奇数的6的整数倍个奇数的3l次方中，3的奇数倍个取负，3的偶数倍个取正，它们的代数和是3的整数倍，且代数和的各位数之和也是3的整数倍。

证明：由[定理7]与[定理8]得悉，l=1、2 对结论成立。

现在假设 l＝h（整数）时结论成立，由[定理7]与[定理8]的证明中得悉，只要假设对于对应项之差成立即可，即

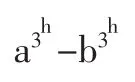
是3的整数倍，那么对于l=h+1

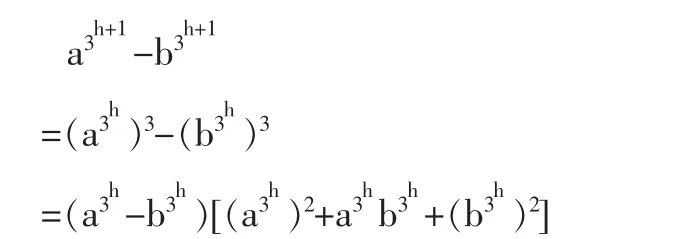
由归纳假设，它是3的整数倍，由文[1]即得后一结论。

[推论3]设m，l为正整数，则第间隔m个奇数的6的整数倍个奇数的3l次方中，3的奇数倍个取负，3的偶数倍个取正，它们的代数和与其代数和的各位数之和乘以任何有限位数的之积的各位数之和都是3的整数倍。

证明：这是[核心定理9]和文[1]的直接推论。

（注：由文[关于数字12的神奇特征]得悉，只要两个正数之差是3的整数倍，那么上述结果对于2h，3h，5h,7h10h次方都是正确的，从而，对于(与每6个一组，不同的间隔m）次方也是成立的）

[1]王仲才.关于数学3的神奇特征[J].江西广播电视大学学报，2010(1).

[2]王仲才.关于3的整数倍的神奇特征[J].江西广播电视大学学报,2011(1).

[3]王仲才.关于数字3的另外神奇特征[J].江西广播电视大学学报，2011(3).

[4]王仲才.关于接连的6的整数倍个正整数、偶数、奇数的3的任意次方的次方的代数和神奇特征[J].江西省广播电视大学学报，2011(4).

[5]王仲才.关于数字12的神奇特征[J].江西广播电视大学学报，2012(2).

O1

A

1008-3537（2012）03-0078-03

2012－06－17

王仲才，男，原南昌大学教授，研究生导师。

刘石玉

校 对：里 仁