浅析多层次自适应算法在数字图像分割中的应用

万 君,吴旻倩

（1.江西广播电视大学 江西 南昌 330046；2.南昌广播电视大学 江西 南昌 330003）

浅析多层次自适应算法在数字图像分割中的应用

万 君1,吴旻倩2

（1.江西广播电视大学 江西 南昌 330046；2.南昌广播电视大学 江西 南昌 330003）

本文简要的介绍了一种新的图像分割方法，该方法对于分割灰度图像有较高的效率和准确率。

代数多层网格；数字图像处理；图像分割；AMG

1 序言

图像分割是指把一幅图像分成彼此不相交的若干个区域，其中每个区域内的像素均有相似或一致的性质，而任何两个相邻接的区域都不具有类似的性质。图像分割的目的就是要将目标物体与背景区分开来，也就是找出图像中物体与背景的边界线。图像分割邻域的技术发展至今，已经提出了多种分割算法。如基于形态学的分水岭方法、基于梯度的图像分割方法、区域增长等。本文着重介绍一种多层次自适应图象分割算法[1]。该算法是在一个来自于物理学的概念代数多层网格的基础上提出的。

2 代数多层网格简介

代数多层网格(AMG)[2]是一种近乎最优的特殊的迭代途径，在偏微分方程数值解中，当离散网格步长h变小时，它的收敛速度并不减慢，而经典的迭代法随h的变小而变慢。因此，代数多重网格法的计算工作量仅与未知量的个数N成正比，比一般迭代法有效得多。

下面简要的介绍代数多层网格的内容。

考虑线性代数方程组

AU＝G,(1)式中:A是一个n×n矩阵,G是已知右端向量;U是未知向量。通过对矩阵A和向量U和G进行重排,系统(1)可以表示为,(2)称为虚拟细网格方程,其中下标F和 C分别表示“细网格”和“粗网格”。为了实现标准的多重网格循环,需要网格之间的转换算子

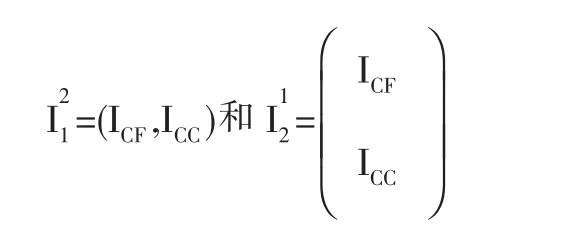
以及粗网格算子A2。

在代数多重网格方法中,一般细网格方程表示为

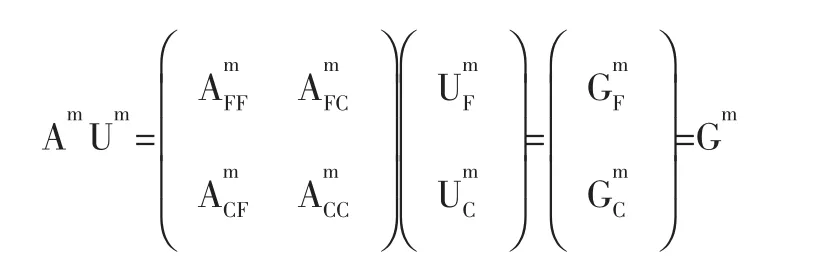
粗网格方程表示为Am+1Um+1=Gm+1

其中,上标 m和 m+1分别相应于“细网格”和“粗网格”。插值算子为

3 多层次自适应算法简介

多层次自适应算法[3]是由Eitan Sharon和Achi Brandt在2006年在自然杂志上发表的针对分割灰度图像而言的算法。该算法是自顶向下，由细到粗的执行过程。具体流程如下图1所示。

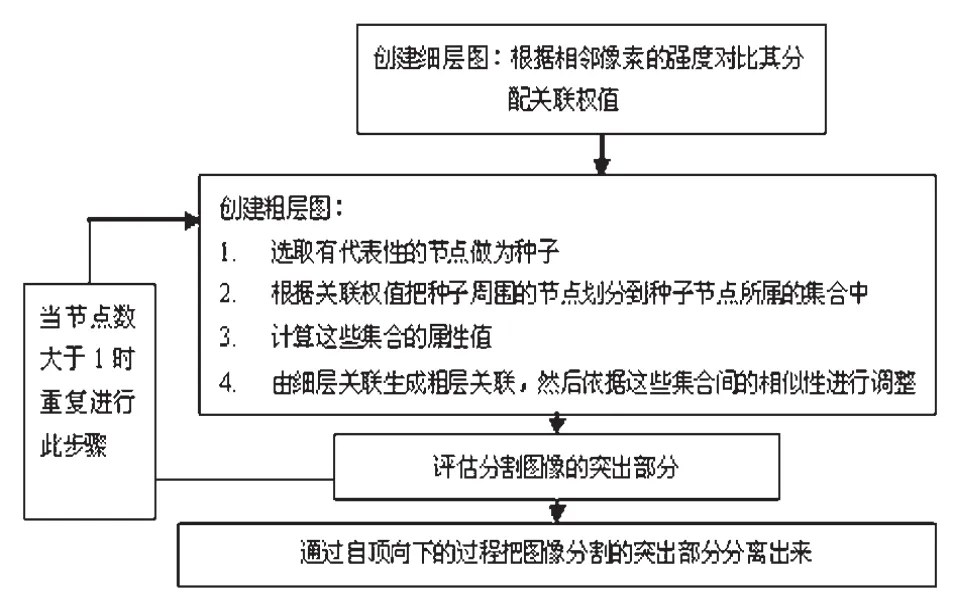
图1 多层次自适应算法流程图

由上图可知，这种算法是将图像看成是节点的集合，每个节点代表一个像素。然后在这些节点中选取一些节点作为种子。根据种子和周围节点的关联权值划分一部分节点到种子的集合中，其中，关联权值和像素的亮度和强度有关。这样形成一个小集合后，集合内的节点都是强关联的。然后继续寻找与集合内性质类似的节点，扩大集合。注意，种子不是只选一个，而是有几个甚至更多，不同的种子开始根据不同的关联权值生成不同的集合，集合和集合之间是弱关联。这样重复迭代执行后，就会出现几个或者更多的差异很大的集合 （重复执行的停止条件是剩余节点小于1）。一般处理后剩2个集合差异最大（背景和目标景物）。最后根据算法评估判断出的突出部分就是需要分割出的目标图像了。

因代数多重网格法的计算工作量仅与未知量的个数N成正比，即O(N)。所以基于AMG快速算法的多层次自适应算法相比过去的那些图像处理方法要快的多，比一般的之前提出的算法都要高效，其时间复杂度随着图像像素的增大呈线性增长。这一优点在介绍AMG法时已经阐明。

4 展望

图像分割技术一直是数字图像处理的关键技术和经典的难题。目前还没有一个算法可以很好的在任意情况下把目标从图像中不费力地分割出来，所以依然有许多是图像工作者投身于图像分割方法的研究中。可以预见，在以后图像分割算法的研究仍将是社会的热点研究课题之一，特别是那些针对实际应用领域，如医学图像、工业应用及遥感应用等领域。

[1]Eitan Sharon,Achi Brandt.Hierarchy and adaptivity in segmenting visual scenes.[J].Nature,2006

[2] Brandt, A. Algebraic multigrid theory: the symmetric case.[J]Appl.Math.Comput.19,23–-56 1986.

[3]杨晖,曲秀杰.图像分割方法综述[J].电脑开发与应用.2005

TP317.48

A

1008-3537（2012）03-0076-02

2012-05-30

万 君，男，江西广播电视大学助理工程师，研究方向：教务管理；

吴旻倩，女，南昌广播电视大学信息中心讲师，研究方向：计算机教学。

刘石玉

校 对：红 农