试析数学中的推理与证明

钱 明

(浙江特殊教育职业学院（筹），浙江杭州 310023)

试析数学中的推理与证明

钱 明

(浙江特殊教育职业学院（筹），浙江杭州 310023)

推理与证明是数学的基础思维过程和方法，它渗透于数学的所有内容.从有关实例入手，分析了推理与证明在数学研究与教学中的运用.

数学；推理；证明

推理与证明是数学的基础思维过程和方法.学习推理与证明，有助于提高学生的逻辑思维能力.推理一般包括合情推理与演绎推理，面对数学问题时，一般是首先运用合情推理进行大胆猜想，然后再运用演绎推理进行证明.推理与证明不是孤立的内容，它贯穿于整个数学课程，渗透于数学课程的各个章节，与函数、数列、立体几何等知识交叉渗透[1].本文将从有关例题入手来分析推理与证明在数学教学中的运用.

1 函数中的推理与证明

例1 已知定义域为[0,1]的函数f(x)同时满足以下三个条件：

I）对任意的x∈[0,1]，总有f(x)≥0；

II）f(1)=1；

III）若x1≥0，x2≥0，且x1+x2≤1，则有f(x1+x2)≥f(x1)+f(x2)成立，称f(x)为“好函数”.

请解答下列各题：

1）若已知f(x)为“好函数”，求f(0)的值；

2）函数g(x) = 2x−1在区间[0,1]上是否为“好函数”？并给出理由；

3）已知f(x)为“好函数”，假定存在x0∈ [0,1]，使得f(x0)∈ [0,1]且f[f(x0)]=x0，求证f(x0)=x0.

解：1）取x1=x2= 0得f(0) ≥f(0) +f(0) ⇒f(0) ≤ 0，又由f(0)≥0，得f(0)=0.

证毕.

评注：本题借助函数充分考查了推理与证明.本题先是给出了“好函数”的定义，“好函数”需要满足题目给出的3个条件.对需要回答的三个问题，第一问中已知f(x)为“好函数”，根据演绎推理的三段论知，大前提是“好函数”的定义，小前提是f(x)为“好函数”，结论是f(x)满足“好函数”的三个条件，从而解得f(0)=0；第二问中要得到函数 () 2x1g x= −在区间[0,1]上是“好函数”这个结论，就要看函数 () 2x1g x= − 是否满足给出的3个条件，经过计算知满足，所以 () 2x1

g x= − 为“好函数”；第三问中利用了推理有证明中的间接证明——反证法证明.

2 数列中的推理与证明

图1 数列{an}

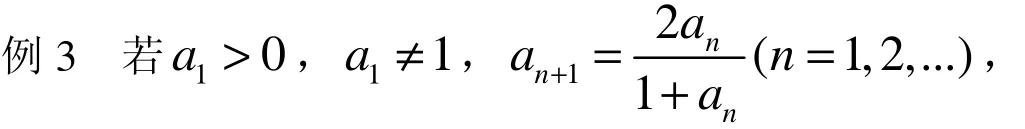
3 立体几何中的推理与证明

图2 斜三棱柱

1）求证CC1⊥MN；

2）类比平面内三角形的余弦定理，写出三棱柱的 3个侧面面积与其中两个侧面所成的二面角之间的关系，并予以证明.

评注：本题是合情推理中的类比推理的应用.平面几何中的许多结论通过类比推理可以得到立体图形的一些性质.另外方法上也可以进行类比，比如，等腰三角形有如下性质：等腰三角形底边的任一点到两腰距离之和等于一腰上的高，运用类比推理，可以推测正三棱锥的相应性质.同样在平面几何上，我们可用“面积法”来求三角形一边上的高的大小.类比上述方法，在空间中可以用“体积法”求三棱锥一个面上的高.

图3 多面体

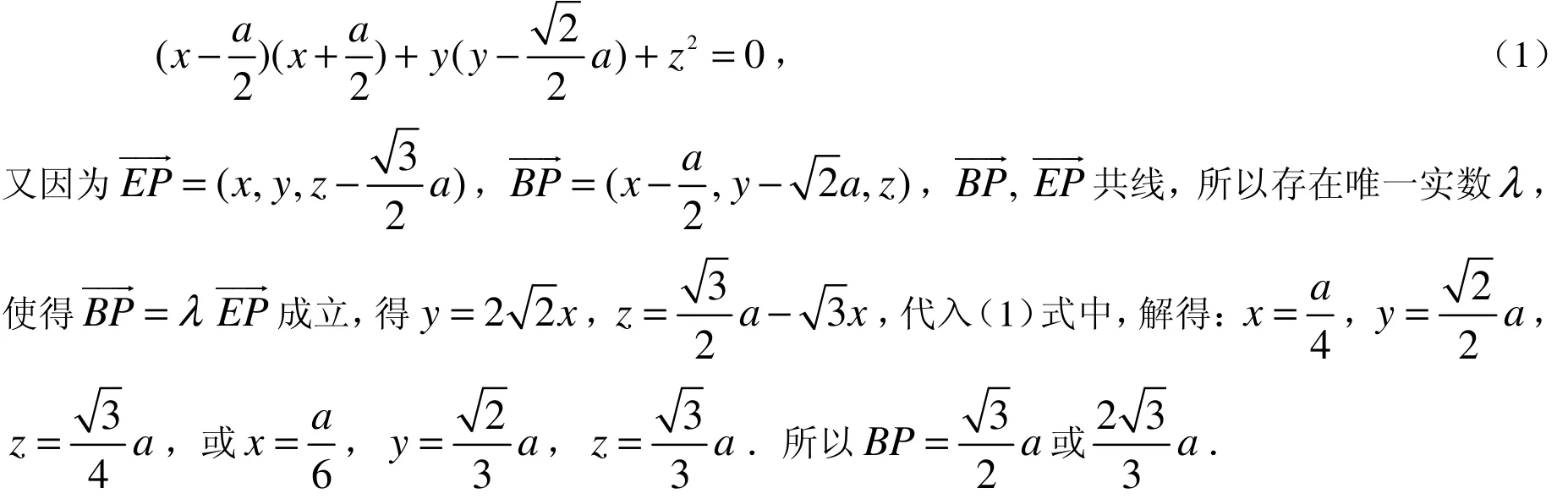
评注：本题是立体几何中的存在性问题，属演绎推理的应用，∠APF为直角，则=0，把一个几何问题通过向量转化为一个代数问题，这样虽然思路简单可行，但不利于对学生空间想象能力和逻辑思维能力的培养.在具体教学中可以引导学生，直接利用演绎推理的逻辑证明方式使问题得到解决.以下为不建坐标系的逻辑法.

4 解析几何中的推理与证明

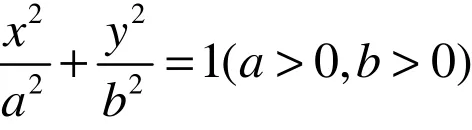
命题的得出是利用了从特殊到一般的猜想，属于合情推理.因为圆锥曲线定义的统一性，双曲线、抛物线可以类比椭圆得到下面的命题：

猜想3 设点M是抛物线y= 2px2(p> 0)上一定点，直线MA与直线MB倾斜角互补，且点A、B在抛物线上，则直线AB斜率为定值.

演绎推理是由一般到特殊的推理，数学的证明主要是通过演绎推理进行的，只要采用的演绎推理的大前提、小前提和推理形式是正确的，其结论就一定是正确的，所以一定要注意推理过程的正确性与完备性[3].以上3个命题都是真命题，猜测后的证明是演绎推理.在解决实际问题时，合情推理具有猜测、发现新结论和探索、提供解题思路的作用，有利于学生创新意识的培养，演绎推理或者逻辑证明能力的培养有助于学生思维能力的发展，能够提高学生的数学素养，两者紧密结合可培养学生创新能力和严谨的推理能力.推理与证明贯穿于整个高中数学课程，教师在进行教学时要有针对性地进行渗透，从而提高学生发现问题和解决问题的能力.

[1]杨文金. 简解数列问题几技[J]. 高中数理化: 高一版, 2007, (1): 12-14.

[2]李技团. 数列问题特殊解法举隅[J]. 数学教学, 2007, (10): 37.

[3]曹时五. 高中数学教材基础知识全解[M]. 北京: 龙门书局, 2008: 20-21.

Study on Induction and Demonstration in Mathematics

QIAN Ming
(Zhejiang vocational College of Special Education, Hangzhou, China 310023)

Induction and demonstration are basic thinking process and method in mathematics. They could be involved in teaching of each chapter of Mathematics course. Based on relative empirical examples, the application of the two in teaching of the course was analyzed.

Mathematics; Induction; Demonstration

(编辑：王一芳)

G42

A

1674-3563(2012)04-0020-06

10.3875/j.issn.1674-3563.2012.04.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2012-04-01

钱明(1967- )，女，浙江杭州人，中学一级教师，学士，研究方向：数学