基于最小二乘法的教学质量评价模型研究

包含丽

(温州大学国际合作学院，浙江温州 325035)

基于最小二乘法的教学质量评价模型研究

包含丽

(温州大学国际合作学院，浙江温州 325035)

评价模型是教学质量评价的核心．利用最小二乘法的原理和方法建立教学质量评价模型，确定评价要素与评价目标之间的关系．实例分析表明，该模型能对教学质量作出客观的评价，克服了专家确定评价模型人为的主观性和随意性，使评价结果更加准确有效．

教学质量；评价模型；最小二乘法；评价要素；回归分析

教学质量评价是根据教学目标的要求，按一定的规则对教学效果作出有价值的判断，是教学管理的重要环节，其目的是为教师改进教学提供有价值的信息，以便更好地促进教学水平的提高．而评价模型是教学质量评价的核心，反映了教学目标和学生的要求，体现了教学效果与教学要素之间的关系，是进行教学质量评价的基础．目前，通常采用层次分析法、模糊综合评判法、灰色系统、聚类分析等方法来建立教学质量评价模型．这些方法能充分吸收专家的知识和经验，体现出各评价因素之间的关系，但这是以人的主观判断为基础，随意性较大，造成评价的失真和偏差，并且不会因为增加专家数量、严格挑选专家等措施而得到根本改善[1-2]．因此，克服人为的主观随意性，建立正确反映评价要素与评价目标（教学效果）之间关系的评价模型，将对教学质量的评价有着重要的意义．本文运用最小二乘法原理和方法建立教学质量评价模型，确定教学要素与教学效果之间的关系，为科学合理地进行教学质量评价和分析提供有意义的参考价值．

1 教学质量评价的输入和输出

教学质量评价是根据评价模型的要求，通过评价要素的测量来确定评价目标的过程．从系统的角度，可以把教学质量评价过程用图1来表示．从中可以看出，教学评价系统由输入（评价要素）、输出（评价结果）和评价模型三部分组成，输入的评价要素是可以测量的量，评价模型反映教学质量输入和输出之间的关系．

要建立教学质量评价模型，首先要确定教学质量评价的输入和输出，即教学质量的评价要素和评价目标．由于教学质量评价是一个复杂的过程，影响教学质量的因素很多，而且各因素的影响程度也各不相同．为了清晰地表达教学质量评价要素和评价目标之间的关系，采用递阶层次结构把教学质量评价体系分成三层[3]，如图2所示．

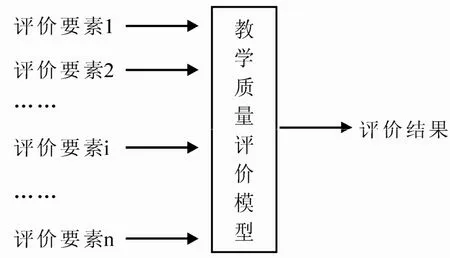
图1 教学质量评价系统

1）目标层：只有一个元素，即为教学质量评价目标值，是我们进行教学质量评价的预定目标或理想结果；

2）指标层：即中间层，包含为实现目标所涉及的各个中间环节，在这里主要是指教学质量评价目标所包含的具体指标，是我们通常意义上讲的教学质量观测点；

3）要素层：表示实现评价目标可供选择的资源、措施、决策方案等，即教学质量评价的影响因素，是可以检测的量，是学校教学资源的体现．

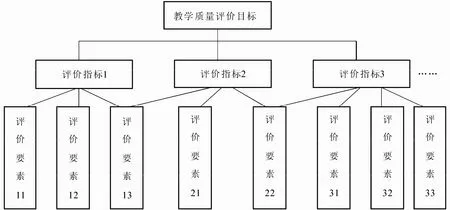
图2 教学质量评价体系结构

根据图2的教学质量评价体系结构，教学质量评价目标可以用向量U=（U1，U2，…，Ui，…，Un）表示．其中，Ui（i=1，2，…，n）为教学质量评价体系结构指标层的第i个指标，可以是教学质量中的考查成绩、课堂教学质量、分析解决问题能力等．

同样，评价指标也可以用数学达式Ui=（Ui1，Ui2，…，Uij，…，Uik）表示，其中Uij为第i个指标的第j个评价要素．例如，课程教学质量指标的评价要素包括教学内容、教师水平、教学设备、教学态度、教学方法等，可以表示为U2=（U21，U22，U23，U24，U25），其中U2为课堂教学质量、U21为教学内容、U22为教师水平、U23为教学设备、U24为教学态度、U25为教学方法．各评价指标依此类推，就可以得到教学质量评价体系要素矩阵．

对评价要素矩阵中任意两个要素Uij和Ukl进行相关性分析，也就是对要素层的每两个元素进行相关性分析，合并相关系数较大的要素，就可以得到教学质量评价要素集P=（P1，P2，…，Pi，…，Pm）．对评价要素集P进行具体的量化为评价要素向量X=（x1，x2，…，xi，…，xm），这就得到了教学质量评价系统的输入．而教学质量评价系统的输出Y是评价目标．

2 基于最小二乘法的评价模型

评价模型反映评价要素向量X与评价目标Y之间的关系，由于教学质量评价要素与评价目标之间的关系比较复杂，考虑教学质量的特点和教学质量评价的可操作性，评价目标和评价要素之间采用多元线性关系来表示．

另一方面，在教学质量评价时，不管是评价要素向量还是评价目标的值，都是通过测量得到的数据．由于受评价主体（学生、专家）主客观因素的影响，都存在随机性误差．为了尽可能地消除测量随机误差给建模带来的影响，采用最小二乘法的原理和方法来建立评价目标Y与评价要素向量X之间的多元线性关系模型．最小二乘法是用于参数估计的数学方法，它使数学模型在残差平方和最小的意义上来拟合测量数据，利用这一点，采用最小二乘法建立的评价模型能够最大程度地反映出评价目标与评价要素之间的关系．

假设评价目标Y与评价要素X之间的多元线性回归模型为：

3 实例分析

根据上述教学质量评价体系和评价模型对某学校的教学质量进行建模和评价．教学质量评价体系如表1所示，指标层为“师资队伍”、“课堂教学”、“实践能力”、“教学管理”，各指标又可展开为评价要素．对指标层下的评价要素进行相关性分析，可以得到教学质量评价的输入项P={教学水平，教学态度，教学内容，教学方法，教学设备，管理水平，服务态度}．

用X={x1，x2，x3，x4，x5，x6，x7}表示输入项P={教学水平，教学态度，教学内容，教学方法，教学设备，管理水平，服务态度}的值，其中x1表示“教学水平”的值、x2表示“教学态度”的值、x3表示“教学内容”的值、x4表示“教学方法”的值、x5表示“教学设备”的值、x6表示“管理水平”的值、x7表示“服务态度”的值．

设计问卷调查①问卷调查表涉及影响教学的因素和教学实施效果两个方面, 即是按教学实施效果对影响教学的因素进行打分评价. 其中, 影响教学的因素包括: 教学水平、教学态度、教学内容、教学方法、教学设备、管理水平、服务态度和总体水平等内容; 教学效果分为好、较好、一般、较差、差5个档次, 设置分值分别为90、80、65、55、40.，发放回收后，取有效的120份问卷调查表随机分成两组：模型样本18组、验证样本6组，每组5份．根据模型样本的18组数据{x1i，x2i，x3i，x4i，x5i，x6i，x7i，yi，（i=1，2，…，18）}和公式（3），利用计算机软件序计算出=（0，0.22，0.15，0.18，0.16，0.11，0.08，0.10），即教学质量评价模型为：

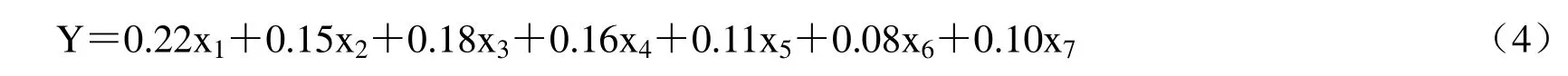
把验证组的8份测量数据代入上述公式（4），可以得到教学质量评价的计算值，如表2所示．以实际值为基准线，画出计算值和实际值对照关系，如图3所示．结果表明评价模型的输出值即计算值很好地逼近评价系统的实际值，较好地反映了教学质量的实际情况，误差不超过±5%．

表1 教学质量评价体系结构

表2 评价模型计算效果比较

4 结 论

本文采用最小二乘法来建立教学质量评价的数学模型，确定各评价要素与评价目标（教学质量）之间的对应关系，实例分析表明该模型能准确地根据各评价要素来描述评价目标，对教学质量给出较客观的评价结果，克服了专家确定评价模型人为的主观性和随意性，使评价结果更加准确有效．同时，正确地评价教学质量，有助于学校充分地调动教学资源，促进教师改进教学方法，克服教学过程中存在的问题，对推动教育改革具有重要的现实意义．

图3 评价模型计算值与实际值

[1] 余雁, 吴文洁. 基于最小二乘法支持向量机的教学质量评价模型[J]. 科技信息, 2008, (29): 29-30.

[2] 钟嘉鸣, 李钉芳. 粗糙集与层次分析法集成的综合评价模型[J]. 武汉大学学报: 工学版, 2008, 41(4): 126-130.

[3] 曲慧琼, 刘华良. 层次分析法在高校形势与政策教学质量评价中的应用[J]. 南华大学学报: 自然科学版, 2008, 22(2): 75-79.

[4] 曲建民. 回归分析在高等教育评价中建立预测模型的应用[J]. 数学理论与应用, 2006, 26(3): 98-101.

[5] 华尔天, 李国富, 毛明杰, 等. 基于最小二法的产品满意度预测模型[J]. 中国机械工程, 2005, 10: 1831-1834.

[6] 包含丽. 基于顾客满意度的成人高等高等教育教学质量评价模型研究[J]. 温州大学学报: 自然科学版, 2007, 28(3): 48-52.

Research on Teaching Quality Evaluation Model Based on Least-squares Method

BAO Hanli
(School of International Cooperation, Wenzhou University, Wenzhou, China 325035)

Evaluation model is the core of teaching quality evaluation. A teaching quality evaluation model was established by using principle and method of least-squares method to determine the relationships between evaluation factors and evaluation objectives. Empirical analysis showed that this model could make an objective evaluation of teaching quality that could overcome the evaluation subjectivity and arbitrariness of experts, and make the evaluation result more accurate and effective.

Teaching Quality; Evaluation Model; Least-squares Method; Evaluation Factor; Regression Analysis

(编辑：封毅)

G420

A

1674-3563(2012)04-0044-05

10.3875/j.issn.1674-3563.2012.04.008 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2012-02-22

包含丽(1979- )，女，浙江东阳人，助理研究员，硕士，研究方向：教学管理，海外华侨教育，企业管理