定时截尾瑞利分布的Bayes估计
王晓红,栾江辉
(吉林师范大学 数学学院,吉林 四平 136000)
瑞利分布是一种重要的寿命分布,引起国内外许多学者的兴趣.关于瑞利分布可靠性的研究,国内外已有一些研究,文[1-2]在Linex损失和对称熵损失条件下研究了瑞利分布参数和参数倒数的贝叶斯估计,文[3]平方误差损失函数和熵损失函数下讨论了Rayleigh分布参数的Bayes估计的比较问题.在可靠性试验中,定时截尾是一种重要的试验形式,但在熵损失函数下,对瑞利分布参数的贝叶斯估计的研究还未发现,为此本文研究在定时截尾情形下瑞利分布参数θ的Bayes估计.
1 参数θ的Bayes估计
设产品的寿命X服从瑞利分布,则其分布函数和概率密度函数的表达式分别为
F(x)=1-e-θx2,x>0,θ>0,
f(x)=2θxe-θx2,x>0,θ>0.
下面讨论熵损失函数下参数θ的Bayes估计.
定义1[4]设随机变量X服从密度函数为f(x,θ)的分布,其中θ为参数.如果δ是判决空间中的一个估计,则熵损失函数为似然比对数函数的数学期望,即
(1)
设X1,X2,…,Xn是来自分布为F(x)的相互独立随机变量序列,在定时截尾下得到的观察值记为(Y1,δ1),(Y2,δ2),…,(Yn,δn),其中Yi=Xi∧T,T为定时截尾时间,满足0 (2) 注:(Yi,δi)(i=1,2,…,n)的联合密度的控制测度已改变. 将(2)式代入(1)式得 (3) 计算得 Eδi=E(IXi≤T)=F(T)=1-e-θT2 (4) (5) 将(4)、(5)式代入(3)式得 易证,这个损失函数关于δ是严凸的. 定理1 在定时截尾情形下,损失函数为熵损失函数时对于任何先验分布,瑞利分布参数θ的Bayes估计为 其中F(x)是瑞利分布的分布函数. 证明 设δ(Y)是参数θ的一个估计,则参数θ的Bayes风险为 令 对该式求导并令导数为零,得 因为φ(δ(Y))为严格凸函数,所以有唯一最小值点,即 是其最小值点.因此参数θ的Bayes估计的一般形式为 定理2 在定时截尾情形下,损失函数为熵损失函数时取参数θ的先验分布为Gamma分布Γ(λ,β),则瑞利分布参数θ的Bayes估计为 证明 参数θ的先验分布为Gamma分布Γ(λ,β),则θ的密度函数为 则联合密度函数为 f(y1,y2,…,yn,δ1,δ2,…,δn)=(2θ)μγe-θρ, 从而θ的后验密度函数为 引理1[5]在给定的贝叶斯决策问题中,假如对给定的先验分布π(θ),θ的Bayes估计δπ(X)是唯一的,则它是容许的. 定理3 在定时截尾情形下,损失函数为熵损失函数时对于任何先验分布,瑞利分布参数θ的Bayes估计是可容许的. 证明 在定时截尾情形下,损失函数为熵损失函数时瑞利分布参数θ的Bayes估计是唯一的,故由引理1,θ的Bayes估计是容许的. 参考文献: [1]陈志强,韦程东,韦莹莹.Linex损失下Rayleigh分布参数倒数的Bayes估计[J].广西科学,2007,14(4):362-364. [2]任海平.对称熵损失函数下Rayleigh分布参数的Bayes估计[J].江西理工大学学报,2010,31(5):64-66. [3]Soliman A.Ahmed.Comparion of Linex and Quadratic Bayes Estimators for the Rayleigh Distribution[J].Commun Statist.-Theory Meth,2000,29(1):95-107. [4]熊常伟,张德然,张怡.熵损失函数下几何分布可靠度的Bayes估计[J].数理统计与管理,2008,27(1):82-86. [5]茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社,1998.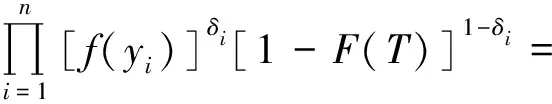


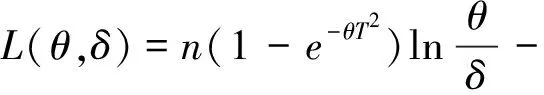
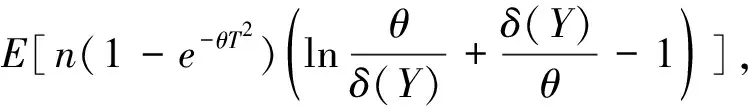


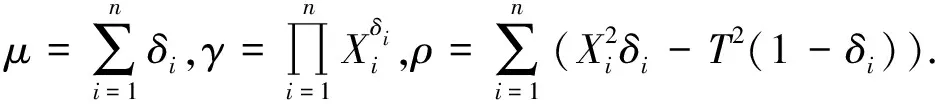


2 参数θ的Bayes估计的可容许性

