Li3N材料的新高压相预测
闫 岩,王丽丽
(长春大学 理学院,吉林 长春 130022)
Li3N是目前为止所获得的碱金属氮化物中唯一热动力学稳定的材料,且是所有已知氮化物中离子性最强的[1].Li3N材料的静态和动力学特性已经得到了人们的广泛研究.经由Li2N层内Li+空穴扩散,研究发现这个材料是一个超离子体[2].近年来,人们研究发现它作为锂离子电池的电解质、储氢材料和GaN合成中的原材料方面的潜在应用,因此引起了人们对其进行广泛且深入的研究,也包括其高压特性[3].众所周知,Li3N材料常压下是以六角结构存在,即α-Li3N,每个单胞中有4个离子,即一个形式单元.晶格常数为a=3.648Å和c=3.875Å,空间群为P6/mmm,其中氮原子是以N3-态稳定存在,这是因为氮是由Li+离子所构成的六角双棱锥包围[4].这个结构是由Li2N层所组成,每一个单胞都是由一个Li原子连接,它占据近邻层中N原子的位置(见图1(a)).

图1 (a)α-Li3N相的晶体结构图(b)新相α'-Li3N的晶体结构图
在大约0.6GPa的压强下,实验发现α-Li3N相变到一个层状六角结构(β-Li3N, P63/mmc).在这个结构中有一个类似于BN的层状结构上下由Li原子连接.在常压下,这个结构是亚稳定的,并且与α-Li3N相共存.随着压强的增加,理论预测当压强达到27.6GPa时,Li3N材料进一步相变到立方结构(γ-Li3N),空间群为Fm3m[5].随后,Lazicki等人[6]实验上证实Li3N材料确实从β-Li3N相变到γ-Li3N相,但是相变发生在36-45GPa的压强区间内,同时指出γ-Li3N结构非常稳定,至少压强达到200GPa,且在这个压强区间材料的压缩性很好.因此,它可以作为内部传压介质的候选材料.
在本文中,我们主要研究了Li3N材料常压结构(α-Li3N)的晶格动力学随压强的变化关系.通过Landau理论,寻找Li3N材料的相变路径.这里我们发现了Li3N材料的一个高压新相,并给出其晶体结构信息,研究了其晶格稳定性.
1 计算方法
本文采用基于密度泛函理论的第一性原理方法进行研究.交换关联函数采用广义梯度近似(GGA)[7].由Fhi98PP程序采用Troullier Martins模守恒(Norm conserving)方案生成Li和N的赝势,其中Li和N的核外价电子排布分别为2s1和2s22p3,核半径分别为2.0 a.u.和1.2 a.u.,确保在计算过程中原子核不发生重叠.经过了谨慎的能量收敛测试,本文计算研究最终选取的能量截断Ecutoff为110 Ry,对于α-Li3N和新结构α'-Li3N 采取Monkhorst-Pack型均匀k点抽样分别为8×8×6和12×12×12,使得总能收敛精度达到1.0×10-3Ry/f.u.[8].采用线性响应理论计算所研究结构的声子频率.声子频率的计算中分别使用8×8×6和12×12×12的k点抽样以确保声子频率收敛到0.01THz,对于常压相α-Li3N和新相α'-Li3N分别采用了4×4×3和4×4×4的q点网格进行力常数的内插,获得声子散射曲线[9].
2 结果与讨论
α-Li3N的平衡晶格常数是通过Murnaghan物态方程[10]将能量作为体积的函数拟合获得.这里我们将本文的计算结果与其它的理论计算和实验结果[11]相比较(见表1),发现晶格常数和体弹性模量与实验结果符合的非常好,误差在3%以内,进而有利地支持了研究中所选择的赝势和交换关联函数.
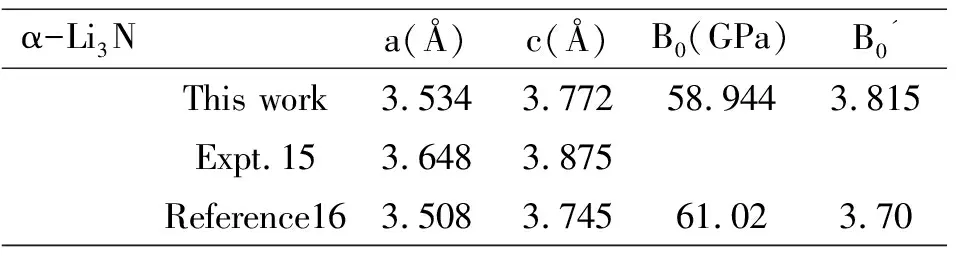
表1 α-Li3N相的平衡晶格常数和、体弹性模量和体弹性模量相对于压强的一阶导数,并与实验结果[10]和理论结果[11]相比较

图2 不同体积下α-Li3N结构的声子散射曲线和声子的分类投影态密度

图3(a)主图为α-Li3N相布里渊区Γ点处的光学支B2g声子频率随压强的变化曲线,插图为声子频率的平方ν2随压强P的变化关系;(b)α-Li3N相的总能随B2g声子模式原子位移的变化关系,其中仅Li2N层中的Li原子沿着[0001]晶向移动,其中箭头给出的是原子位移的方向.
图2给出的是不同体积下α-Li3N结构的声子散射曲线和声子分类态密度,其中实验获得的中子非弹性散射谱的数据(方形和三角形)被引入与我们的计算结果比较[12].结果表明我们的计算结果,除了光学模式存在微小的偏差外,与实验数据符合的很好.因为考虑了动力学矩阵的非分析项,所以纵向光学支和横向光学支在Γ点发生劈裂.值得注意的是横纵光学支的劈裂取决于接近Γ点的方向,而劈裂的幅度能够通过玻恩有效电荷张量和介电张量来表征[13].横纵光学支的劈裂也指出α-Li3N的各向异性特性.这导致在布里渊区的不同方向上横纵光学支劈裂不同.从图中的声子分类态密度看出在α-Li3N材料中Li和N原子之间的振动存在着强烈的耦合作用,这是由于它们原子质量相近的缘故.同时,我们发现随着体积的减小,Γ点处的B2g模式的频率值减小.当体积V=0.938V0(V0是实验的平衡体积)时,B2g模式软化到虚频,这就意味着α-Li3N结构不稳定.
图3a给出的是B2g模式的频率随体积的变化曲线,而插图中给出的则是Γ点处B2g模式声子频率的平方值随压强的变化曲线.声子频率平方与压强间存在着近乎完美的线性关系.这一点与压强引起软膜相变的Landau理论相一致,其中零声子频率所对应的压强即为α-Li3N相变到新相(这里我们称为α'-Li3N)的相变压力点[14].通过对软化的B2g声子模式的本征矢量进行分析,发现在常压的α-Li3N结构中仅仅Li2N层中的Li原子沿着[0001]方向振动,具体的振动方向在图3(b)的插图中已给出.稳定的高压相可以通过不稳定的B2g声子模式的本征矢量进行微小的位移,同时进行全局能量优化,能量最小值所对应的结构即为能量更稳定的新结构.图3(b)指出压强为2.5GPa时,形成了一个能量势井.通过精确的优化,获得了一个新的六角相结构(即α'-Li3N),空间群为P-3m1.图1(b)给出的是其对应的晶体结构图.从图中可以清楚看出α'-Li3N与α-Li3N的区别是Li2N层发生了扭曲,其中的Li原子脱离了原来的平面.α'-Li3N的具体结构信息为晶格常数a=3.5315Å和c=3.7716Å,其中Li原子占据1b(0,0,1/2)和2d(1/3,2/3,z)位,而N原子占据1a(0,0,0)位置.为了进一步研究新提出的α'-Li3N相动力学的稳定性,图4给出了其在V=0.9202V0时的声子散射曲线和声子分类态密度.从图中可以看出在整个布里渊区内没有虚频声子存在,这也就是说α'-Li3N结构是动力学稳定的.

图4 当V=0.9202V0时,新相α'-Li3N的声子散射曲线和声子的分类态密度
3 结论
采用第一性原理的方法研究了Li3N材料常压相α-Li3N结构的晶格动力学和结构相变.通过Landau理论,我们预测了当压强P=2.8GPa时,α-Li3N结构将会相变到一个新的六角相,即α'-Li3N.我们希望有进一步的XRD数据和拉曼实验能够证实此相结构的存在.
参考文献:
[1]A. Rabenau, in Festk¨orperprobleme (Advances in Solid State Physics) edited by J. Treusch (Vieweg, Braunschweig, 1978), vol. 18, p. 77.
[2]E. Bechtold-Schweickert, M. Mali, J. Roos, D. Brinkmann,Phys. Rev. B 30, 2891(1984).
[3]A. Rabenau, H. Schulz, J. Less Common Metals 50, 155(1976); A. Rabenau, Solid State Ionics 6, 277 (1982).
[4]H.J. Beister, Sabine Haag et al., Angew. Chem, Int. Ed. Engl. 27, 1101 (1988).
[5]J.C. Sch¨on, M.A.C. Wevers, M. Jansen, J. Mater. Chem. 11, 69 (2001).
[6]A. Lazicki, B. Maddox, W.J. Evans, C.S. Yoo, A.K. McMahan, W.E. Pickett, R.T. Scalettar, M.Y. Hu, P. Chow. Phys. Rev. Lett. 95, 165503 (2005).
[7]J.P. Perdew, K. Burke, Int. J. Quantum Chem. 57, 309 (1996); J.P. Perdew, K. Burke, M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996).
[8]N. Troullier, J.L. Martins, Phys. Rev. B 43, 1993 (1991); H.J. Monkhorst, J.D. Pack, Phys. Rev. B 13, 5188 (1976).
[9]S. Baroni, P. Giannozzi, A. Testa, Phys. Rev. Lett. 58, 1861 (1987); P. Giannozzi, S. de Gironcoli, P. Pavone, S. Baroni, Phys. Rev. B 43, 7231 (1991).
[10]F.D. Murnaghan, Proc. Natl. Acad. Sci. USA. 30, 244 (1944).
[11]A.C. Ho, M.K. Granger, A.L. Ruoff, P.E. Van Camp, V.E.Van Doren, Phys. Rev. B 59, 6083 (1999).
[12]W. Kress, H. Grimm, W. Press, J. Lefebvre, Phys. Rev. B 22, 4620 (1980).
[13]N.W. Ashcroft, N.D Mermin, Solid State Physics (HRM International Editions, Phyiladelphia 1976) p. 548.
[14]G.A. Samara, P.S. Peercy, in Solid State Physics, edited by H. Ehrenreich, F. Seitz, D. Turnbull (Academic, New York, 1981), vol. 36.

