改进的神经预测控制及其应用

任怀庆，葛兴国

(1.通化师范学院 计算机学院，吉林 通化 134001；2.空军航空大学，吉林 长春 130022)

自从人工神经网络实现以来，各种各样的神经网络已经被设计并应用于诸多领域.大多数神经网络采用基于梯度的监督学习算法，包括前馈神经网络、多层感知器、各种类型的递归神经网络、径向基函数神经网络，以及一些具有特殊结构的神经网络，如时滞神经网络.神经广义预测控制NGPC(Neural Generalized Predictive Control)[1，2]是由Donald Soloway提出的，NGPC是对1987年Clarke的GPC(Generalized Predictive Control)的改进.在NGPC方法中，用神经网络系统识别技术代替了标准的建模技术，并且滚动时域优化方法采用了Newton-Raphson算法，但是在Newton-Raphson算法中需要计算Jacobian矩阵和Hessian矩阵，在计算Jacobian矩阵和Hessian矩阵中，每一项都是计算代价函数对控制输入的一阶、二阶导数，对于时滞较大的系统，需要计算的时域值较多，因此Jacobian矩阵和Hessian矩阵的计算量可能较大，使得系统控制的实时性能变差.本文将时滞神经网络用于神经广义预测控制中对被控系统的识别，直接用时滞神经网络的输出与输入关系替代以上导数的计算，极大的提高了系统控制的速度.

1 时滞神经网络

时滞神经元[3]如图1，是在普通神经元的每一个分支上加入了时间延迟因子q-τ，由图可知，神经元的输出与输入之间的关系为：

(1)

其中，wi是神经元的权值，τi为第i个输入的时间延迟，σ(·)为神经元的非线性激活函数.

图1 时滞动态神经元结构

图2 时滞神经网络结构

具有三层结构的时滞神经网络如图2所示，“●”表示动态时滞神经元，“〇”表示线性输出神经元，由于引入了时间延迟因子，因此，时滞神经网络的更新规则包括两类，一个是权值的更新规则，一个是时间延迟因子的更新，权值的更新与普通神经网络的更新一致，可以采用最陡下降算法，本文中只给出时间延迟因子的更新规则.

对于输出层：

(2)

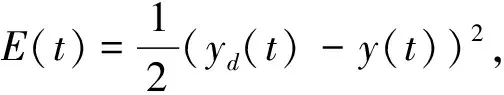
(3)

(4)

其中，上角标I、H分别表示输入层、隐藏层，T表示取样周期.为了防止反传算法抖动，通常间隔P个周期使用平均值进行更新.

对于隐藏层更新算法与输出层类似，只不过需要比输出层多进行一步反传，此处省略.

2 改进的广义预测控制结构

改进后的广义神经预测控制结构如图3所示，NNI为未知非线性系统的神经网络识别器，CFM仍然为代价函数，在神经识别模型结构中，将传统的前馈神经网络替换成了新的具有时间延迟线结构的时滞神经网络，使得神经网络的输出对输入的一阶导数及二阶导数可在一次反传中得到，大大提高了使用传统前馈网络识别通过迭代计算Jacobian矩阵和Hessian矩阵的计算速度.

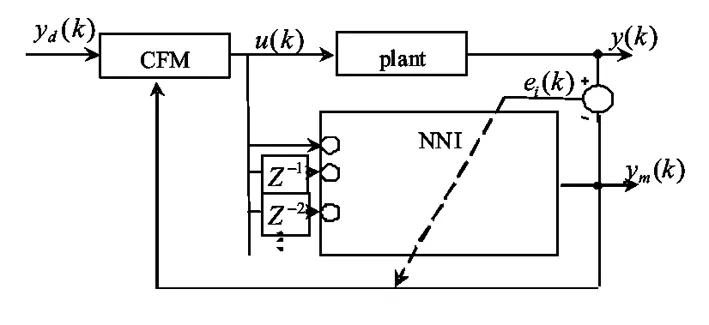
图3 改进后的神经广义预测控制结构

3 仿真控制结果

基于前面给出的改进方案，将其用于电磁悬浮系统控制问题.其运动控制方程为：

(5)

其中y(t)为磁体与电磁线圈的距离，i(t)为电磁线圈中的电流强度，M为永磁体的质量，g为重力加速度常数，参数β为摩擦系数，α为由电磁线圈匝数决定的磁场强度，本仿真实验当中，取采样周期为0.1秒，β=12，α=15，g=9.8，M=3，其余参数与文献[4]中一致.仿真结果见图4～图6，图4为神经网络的训练集.由图可知，训练集是可接受的.图5为神经网络的识别性能曲线，由图可知，神经网络的识别速度是很快的，只需10个回合的训练即可收敛到可接受的程度.图6为控制性能对比曲线，由图可知，改进的方案比原始的基于BP算法的前馈神经网络的性能要好的多，图中实线部分为改进方案的控制性能.

图4 神经网络训练集

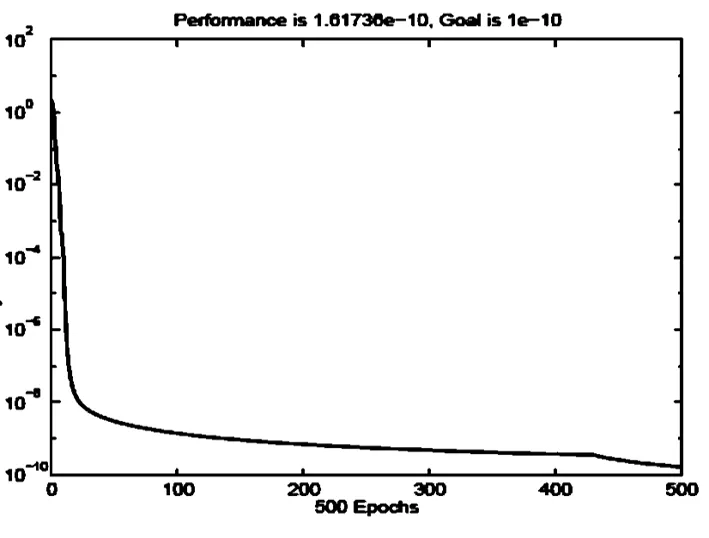
图5 时滞神经网络对被控系统的识别曲线

图6 改进的神经广义控制性能与传统方案的对比

4 总结

本文讨论了广义神经预测控制及其在非线性控制方面的应用，指出了广义预测控制在实时控制方面的限制，即当被控系统时滞较大时，广义神经预测控制的局限性，并改进了广义预测控制的结构方案，使用具有时间延迟线结构输入的时滞神经网络作为被控系统的识别器，大大缩减了广义预测控制算法的计算复杂度，实验表明此种控制方案很有效.

参考文献：

[1]Soloway D I，Haley P J.Neural generalized predictive control:A Newton-Raphson implementation [J].NASA TM-110244，1997，1-18.

[2]Soloway，D.,P.J.Haley，Neural Generalized Predictive Control [J].Proceedings of the 1996 IEEE International Symposium on Intelligent Control，1996，277-281.

[3]Yazdizadeh，A.，Khorasani，K.Adaptive Time Delay Neural Network Structures for Nonlinear System Identification[J].Neurocomputing，2002，47(1-4)：207-240.

[4]任怀庆，梁艳春，孙亮.基于神经网络的滚动时域优化控制[J].北京邮电大学学报，2009(2).