瞬态瑞利波法定量分析二维空洞的形状参数和位置
郭德平,江刚,李铮,钟炜华,李金鑫,周小平,5b
(1.叙镇铁路有限责任公司,云南 昭通 657900;2.贵州大学 土木工程学院,贵阳 550003;3.重庆市城市建设投资(集团)有限公司,重庆 400015;4.江西应用技术职业学院,江西 赣州 341000;5.重庆大学 a.土木工程学院;b.山地城镇建设与新技术教育部重点实验室,重庆400045)
随着地下工程的大力发展,地质勘探显得越来越重要。空洞的存在对建筑物产生沉降和破坏作用,影响建筑物的正常使用,使公路、铁路和机场跑道等路基塌陷而导致交通中断等。在弹性波波场能量中,瑞利波的波场能量占比高达67.3%,且瑞利波在介质中传播的动态响应能反映出岩土体的物理属性。因此,笔者采用时频分析法和频谱分析法得到空洞的形状参数和位置。
瑞利波是瑞利(Rayleigh)[1]在1887年发现的弹性波。Stkooe等[2]利用瞬态瑞利波法进行勘探实验,得到了瑞利波在介质中的相速度分布,并提出了面波频谱分析方法(SASW)。Park等[3]基于多道面波分析原理得到了瑞利波多阶模式的频散曲线。Nasseri-moghddam等[4-5]提出了瑞利波衰减分析法(AARW),根据瑞利波传播过程中的能量模式转换等的特性分析了空洞的位置和埋深。孙宏祥等[6]采用激光激发瑞利波探测了材料表面缺陷的角度。Xia等[7]利用瑞利波在空洞尖端处的衍射波确定了空洞的位置。周文宗[8]对含有空洞介质中的瑞利波频散曲线进行了正反演研究。冯治国[9]利用瞬态瑞利波法对岩溶路基注浆质量进行了检测,并取得了良好的效果。刘中宪等[10]采用间接边界积分方程法对衬砌隧道中入射瑞利波的二维散射问题进行了分析。Chai等[11]通过数值模拟研究了激励源和空洞埋深对瑞利波的影响。张献民等[12]通过数值模拟总结了地下管道的形状和管径大小对瑞利波信号的相应规律。Shao等[13]基于夏江海的研究提出了利用广义S转换的方法探测空洞的埋深。柴华友等[14]重点分析了表面源激发的瑞利波在层状介质中的传播特性。已有研究大部分是理论研究,并没有对空洞的形状参数和埋深进行系统分析。
笔者基于上述研究分析了瑞利波的波动特性,并采用有限元方法对含有空洞的介质模型进行了数值模拟,提出了确定空洞形状参数和位置的计算方法:采用入射瑞利波和反射瑞利波的时间差法确定了空洞的位置和水平尺寸;采用临界频率干扰法确定了空洞埋深;采瑞利波衰减率法获得了空洞竖向尺寸。
1 瞬态瑞利波法
瑞利波能够应用于空洞检测,主要是利用瑞利波在介质内传播的两个特性:1)瑞利波的勘探深度和能量主要集中在一个波长范围内,且波长不同,其穿透深度也不同。2)瑞利波沿着介质表面传播时,遇到空洞会发生反射和透射,同时发生模式转换。与此同时,由于受到空洞的影响,瑞利波的能量发生衰减。
瞬态瑞利波探测法原理是在地面某一点处施加冲击力,地面会产生一定频率范围且由多个简谐波组成的瑞利波,用布置在地表上的检波器采集数据得到瑞利波的时域图和频谱,并采用幅值分析法和相位差分析法对瑞利波频谱处理得到瑞利波的频散曲线。笔者同时采用时域和频谱分析法,对接收到的弹性波波形特点和频谱进行分析,得到空洞形状参数和位置。
2 空洞形状参数和位置的确定方法
2.1 入射瑞利波和反射利波时间差法
如图1所示,在激励源用下,介质中产生3种弹性波:纵波(P)、横波(S)和瑞利波(R)。纵波传播速度比较快,但波场能量比较弱,因此,在模拟分析中忽略纵波,横波和瑞利波的传播速度非常接近,在短时间内分辨不出。瑞利波沿着介质表面传播过程中,遇到空洞边界,一部分波发生反射形成反射瑞利波,一部分波在边界处积聚并最终消散,一部分瑞利波在边界处发生模式转换形成衍射横波和衍射纵波,另一部分波则直接透射过去形成透射瑞利波。因此,可以利用入射瑞利波和反射瑞利波的时间差来探测空洞的位置(空洞边界位置),同时,采用对称布置的方式来确定空洞水平方向的尺寸。计算式为
(1)

图1 瑞利波传播示意图Fig.1 The diagram of Rayleigh wave
式中:l为接收点与空洞的水平距离;tR为入射瑞利波到达时刻;tRR为反射瑞利波到达时刻;VR为瑞利波传播速度。
根据接收器接收的波形图,找到入射瑞利波和反射瑞利波的时间,根据式(1)即可确定空洞的位置和空洞水平方向的尺寸。
2.2 临界干扰频率法
研究表明[15],瑞利波能量主要集中在一个波长范围之内,因此,探测深度为一个波长。根据瑞利波的这一特性,可以找到瑞利波的频率与空洞埋深的定量关系。
激励源采用中心频率的雷克子波,激励产生瑞利波的主要频率在两倍的中心频率内,而中心频率左右的频率为最优频率带。空洞埋深在某一频率对应的波长范围内,则空洞对该频率的瑞利波产生影响,损耗其能量,空洞埋深超出某一频率对应的波长,则空洞不对瑞利波产生影响。波长和频率的对应关系为
(2)
式中:λR为瑞利波波长;f为瑞利波频率;VR为瑞利波速度。
提出“临界干扰频率”的概念,即未被空洞影响瑞利波的临界频率。将接收器接收到的时域图经过FFT变换成频谱,根据有空洞和无空洞的频谱对比来找到临界干扰频率,反算空洞的埋深。
2.3 能量衰减率法
瑞利波的波场能量衰减除自身的衰减外还有空洞对瑞利波的干扰。空洞对瑞利波能量的影响主要是瑞利波的反射,即在空洞边界处瑞利波能量积聚并最终消散,另外一部分瑞利波发生能量模式转换形成横波和纵波。由此认为瑞利波的能量损失主要由靠近激励源的空洞边界引起,空洞边界越长,瑞利波的能量衰减越大,透射瑞利波的能量越小。因此,可以利用瑞利波的能量衰减率推算空洞竖向尺寸。
可以用能量衰减率法定量分析空洞的竖向尺寸。能量衰减率为有空洞和无空洞模型中某接收点处瑞利波频谱中某频率对应的幅值差与无空洞瑞利波幅值的比值,即
(3)
式中:Ar(fi)为频率fi对应的瑞利波衰减率;Ai为有空洞模型中频率fi对应瑞利波的幅值;A0i为无空洞模型中频率fi对应瑞利波的幅值。
3 案例分析
借助有限元软件ABAQUS动力学模块模拟瞬态瑞利波,对含有空洞的模型进行数值模拟。瞬态动力学能够用于分析结构的动力响应。
3.1 模型参数设置
3.1.1 激励源 采用瞬态瑞利波法在野外勘探中,激励源一般采用落重法来激发弹性波,要求锤击产生的波由多种地震子波组成,因此,选择震源形式时,要选择一个时间脉冲函数子波,其频谱高于中心频率,并且能够迅速减少。雷克子波满足上述要求,且模拟结果精度高,波形也与野外实测波形非常接近。其具体形式为
F(t)=A[1-2π2f2(t-t0)2]e-π2f2(t-t0)2
(4)
式中:A为激振力最大振幅,用来调整激振力大小;f为中心频率;t0为瑞利波滞后时间。图2为频率f=30 Hz的时域图。
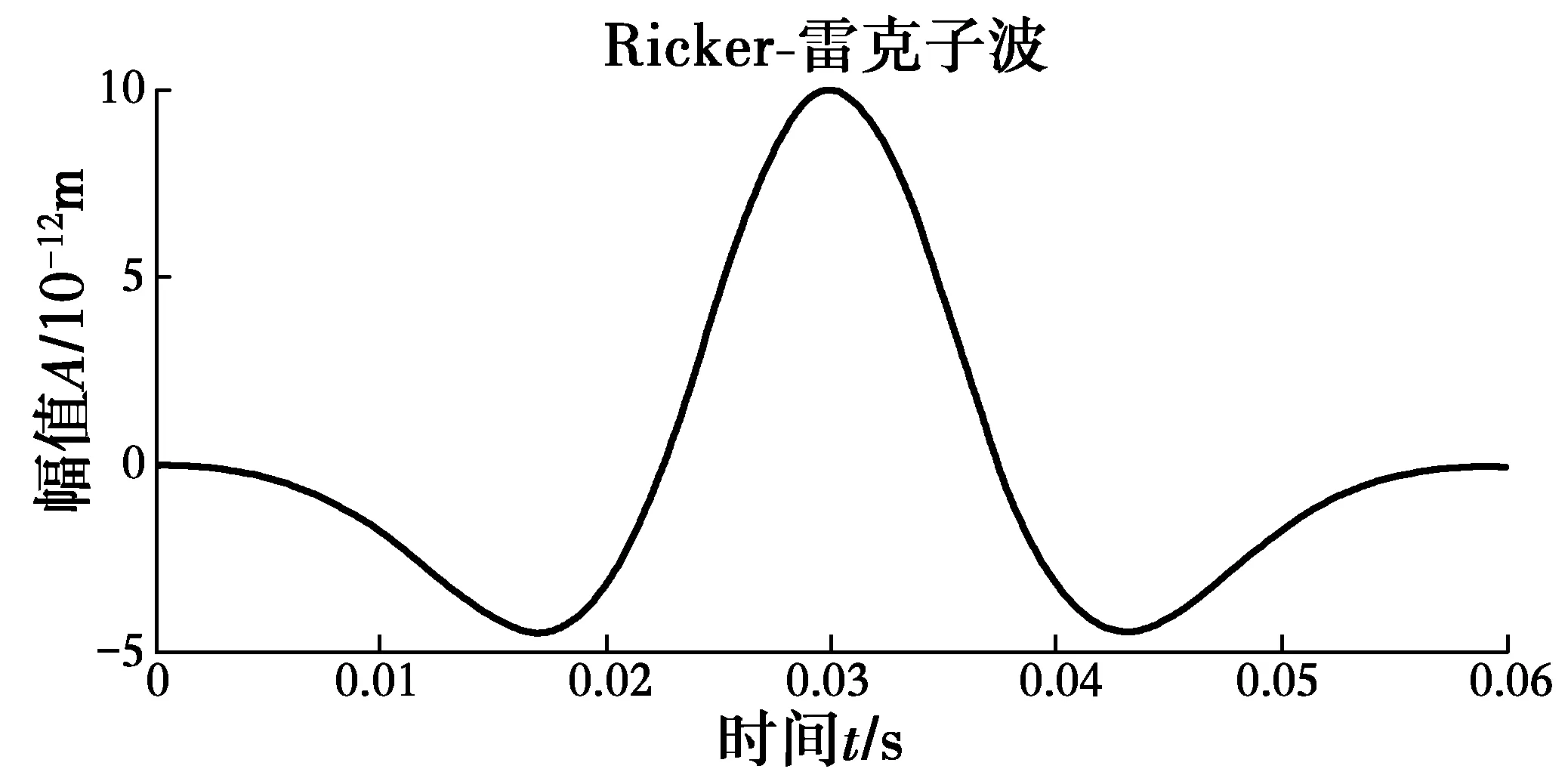
图2 雷克子波
3.1.2 边界条件设置 采用均匀半无限空间介质的模型,为了降低边界条件对模拟结果的影响,采用刘晶波等[16]提出的等效二维一致粘弹性人工边界对模型边界进行处理。
3.2 空洞水平位置确定
为了与野外实地检测条件相符,模型尺寸为:L=100 m,H=50 m,空洞为边长2 m的方形,空洞上边界与模型表面的垂直距离(即空洞埋深)h分别设置为2.0、2.5、3.0、3.5、4.0、4.5、5.0、5.5、6.0、6.5、7.0 m共11种工况,空洞设置在距离激励源40 m处。激励源与空洞距离为40 m,中心频率为30 Hz,幅值为a=1×10-11m。根据采样定律得到数据的采样时间间隔为5×10-4s,总采样时间为3.0 s。接收器设置在距离激励源右侧10 m处。网格采用等边三角形,边长为0.5 m。模型边界采用粘弹性人工边界。介质材料为灰岩,密度为ρ=2 500 kg/m3,弹性模量为E=1.89 GPa,泊松比为μ=0.3,则根据式(5)~式(7)可以得到纵波、横波和瑞利波的传播速度,分别为VP=1 008.8 m/s、VS=539.23 m/s、VR=500.24 m/s。
(5)
(6)
(7)
具体模型如图3所示。
图4所示为接收器接收的波形图。当介质中无孔洞时,波形图只有一个比较大的峰值点p。因为弹性波中瑞利波的波场能量最强,认为此峰值为入射瑞利波达到接收器的时间点。介质中存在空洞时,波形图出现两个峰值点p和q,p点即为入射瑞利波的接收时间点,q点则为反射瑞利波的接收时间点。因为在弹性波中瑞利波的波场能量最强且衰减最慢,故在反射波中,反射瑞利波的波场能量也最强。
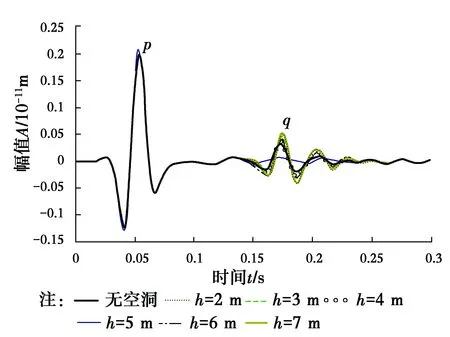
图4 波形图
由图4可知,反射瑞利波到达接收器的时间不受空洞埋深的影响。因此,提取计算波形图中入射瑞利波和反射瑞利波的时间,并计算空洞的位置,计算结果误差分析如图5所示,不同埋深的空洞水平位置计算误差均在2.0%以下,满足实际工程的精度要求。
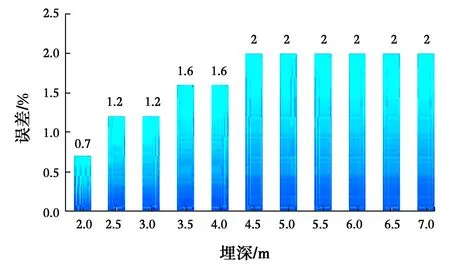
图5 水平位置计算误差Fig.5 Calculation error of horizontal
另外,由瑞利波的波动方程可知,瑞利波的振幅随着深度的增加而衰减,瑞利波的波场能量随深度增大而减弱。因此,由于能量减少的原因,空洞加深,其检测精度会降低,相对误差变大。
3.3 空洞埋深确定
模型尺寸设定为:长L=100 m,高H=50 m。震源为中心频率50 Hz的雷克子波,t0为0.02 s,振幅大小为1×10-11m,作用在距离模型左边界40 m处。网格采用等边三角形,边长为0.5 m,吸收边界采用等效粘弹性人工边界。采样时间间隔为Δt=0.2 ms,采样总时间为t=1.5 s,空洞大小为2 m×2 m,空洞设置在距离模型左边界55 m处(空洞形心与模型左边界的距离),空洞埋深为5 m,具体模型如图6所示。
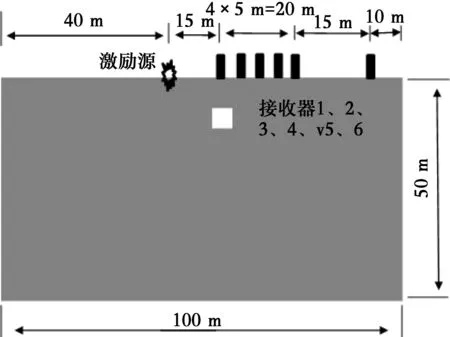
图6 模型示意图Fig.6 The schematic diagram of the numerical
将接收到的波形图(时域图)应用FFT变换成频谱,并将无空洞和空洞埋深为5 m的频谱作对比,找出临界干扰频率(图中交点所对应的频率)。由于接收器距离空洞太近,受杂波影响大,因此,去掉接收器1和2的数据,模拟结果如图7所示。
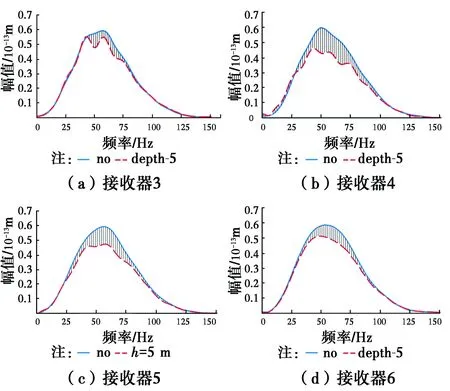
图7 频谱图
根据图7中各接收器处的频谱图,找出有空洞和无空洞频谱交点所对应的频率,该频率即为临界干扰频率,然后根据临界干扰频率计算空洞埋深。
由图8可知,各接收器处计算得到的空洞埋深误差均在10%以下,由4个接收器处的临界干扰频率均值计算得到空洞埋深为4.7 m,误差为6%,精度达到工程要求,说明该方法可行。
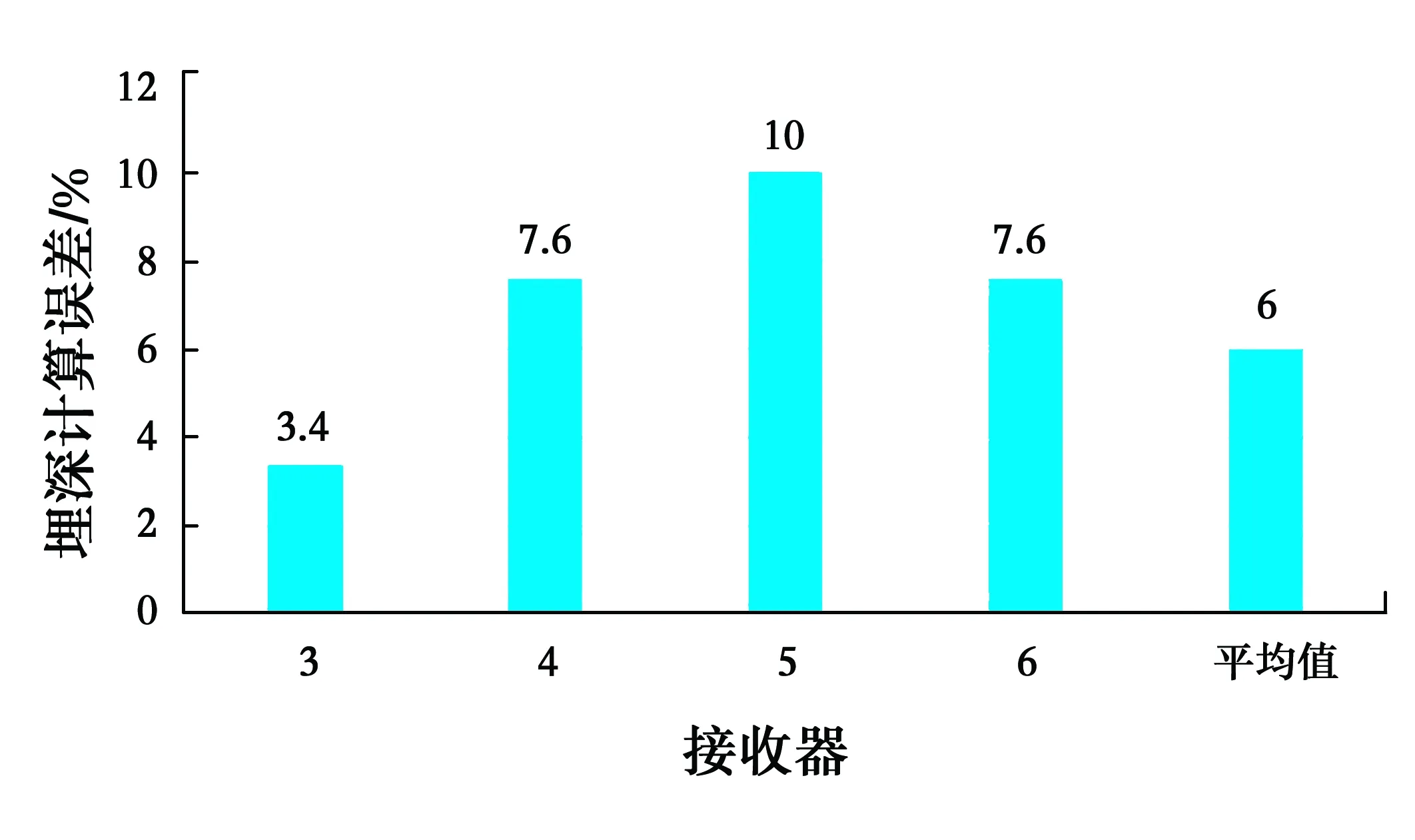
图8 空洞埋深计算误差(h=5 m)Fig.8 Calculation error of depth of
为了使该方法具有普遍性,另外设置空洞埋深分别为6 m和7 m的模型进行分析,其计算结果如图9所示。从图9可以看出,空洞埋深计算误差不超过11%,误差均在允许范围内。
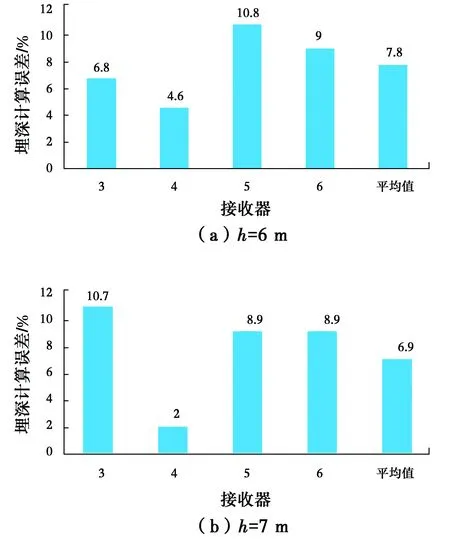
图9 空洞埋深计算误差Fig.9 Calculation error of depth of
3.4 空洞竖向尺寸确定
为了找到空洞竖向尺寸与瑞利波衰减率的定量关系,设置空洞埋深为5 m,空洞的几何形心与激励源的水平距离为20 m,空洞大小分别为2.0 m×2.0 m、2.5 m×2.5 m、3.0 m×3.0 m 、3.5 m×3.5 m、4.0 m×4.0 m、4.5 m×4.5 m、5.0 m×5.0 m 共7种工况。接收器设置3个,分别为接收器1、接收器2和接收器3,3个接收器距离空洞形心的水平距离分别为5、15、30 m。其他模型参数同4.3节中的模型参数。
将各接收器得到的时域图经FFT变换成频谱图,并从频谱图中提取频率为40、50、60 Hz的瑞利波幅值,将瑞利波的衰减率绘制成如图10所示。
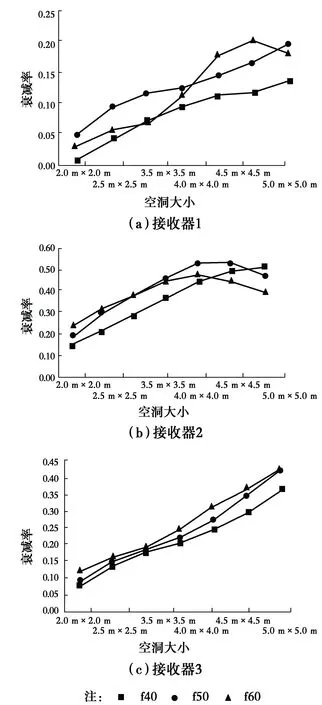
图10 衰减率与空洞大小关系Fig.10 Relationship between attenuation
从图10可以看出,接收器3处的瑞利波不管是低频还是高频其衰减率比较稳定且比较相近,因此,选用接收器3处的瑞利波衰减率来定量分析空洞竖向尺寸的大小。选用中心频率为50 Hz对应的瑞利波进行分析。
将接收器3处的50 Hz对应的瑞利波的衰减率曲线进行拟合,得到式(8)。
Ar(50 Hz)=0.096 89d-0.109 63
(8)
式中:Ar为瑞利波衰减率;d为空洞竖向尺寸。
式(8)的拟合方差为0.974 27,拟合效果较好,说明用式(8)定量计算空洞竖向尺寸合理。
为了验证式(8)的准确性,现设置埋深为5 m,空洞大小为2.25 m×2.25 m、2.75 m×2.75 m、3.25 m×3.25 m 、3.75 m×3.75 m 的4种工况进行分析,计算结果如图11所示。
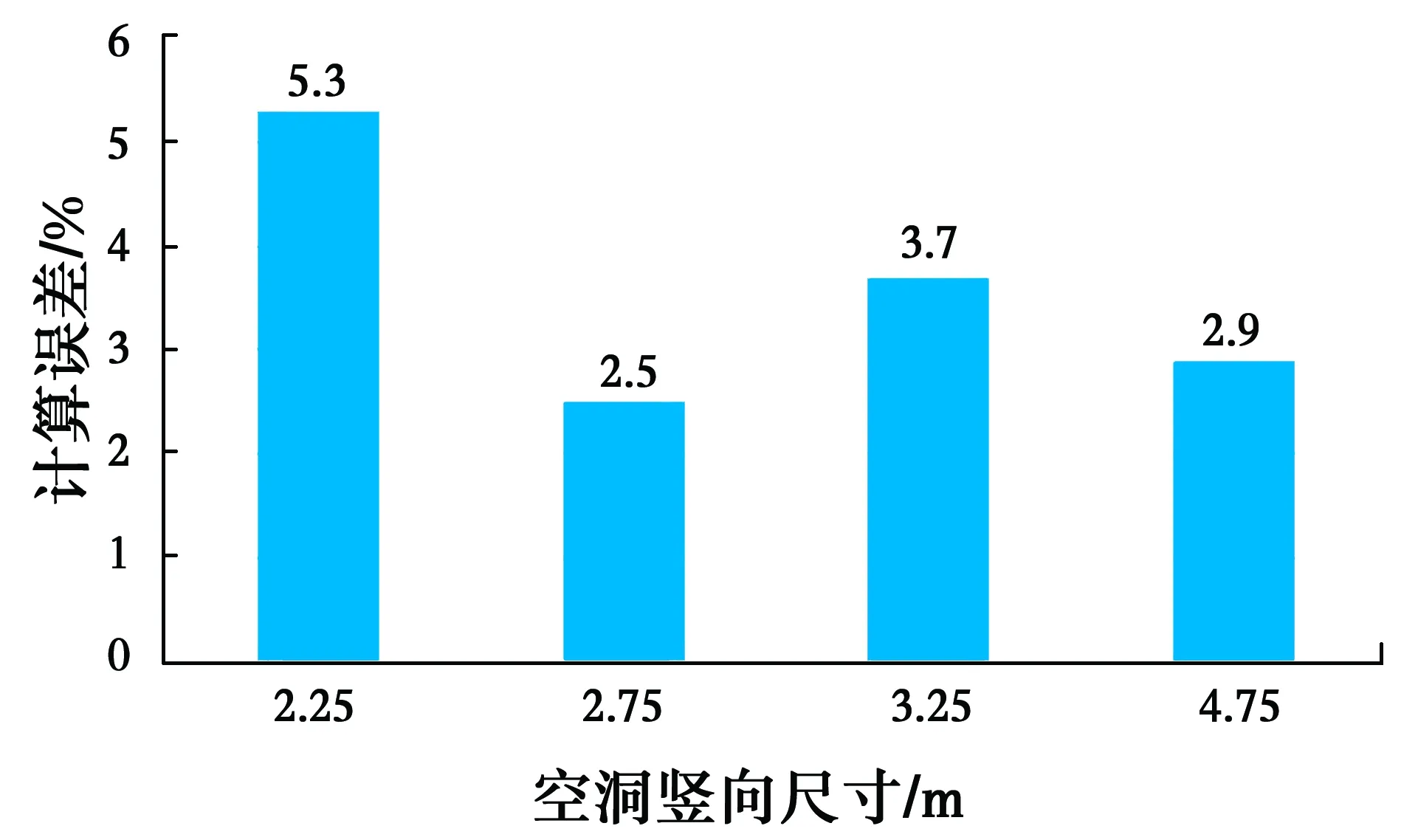
图11 空洞竖向尺寸计算误差Fig.11 Calculated error of vertical size of the
从图11可以看出,由式(8)计算得到的空洞竖向尺寸误差均在6%以下,有较高的准确度。
4 工程实例
项目为拟建的地下管道,深度4 m左右。采用瞬态瑞利波法探测地下管道。为了能够与地层结构区分,设置了131个采样点。采集到的原始波形图如图12所示。
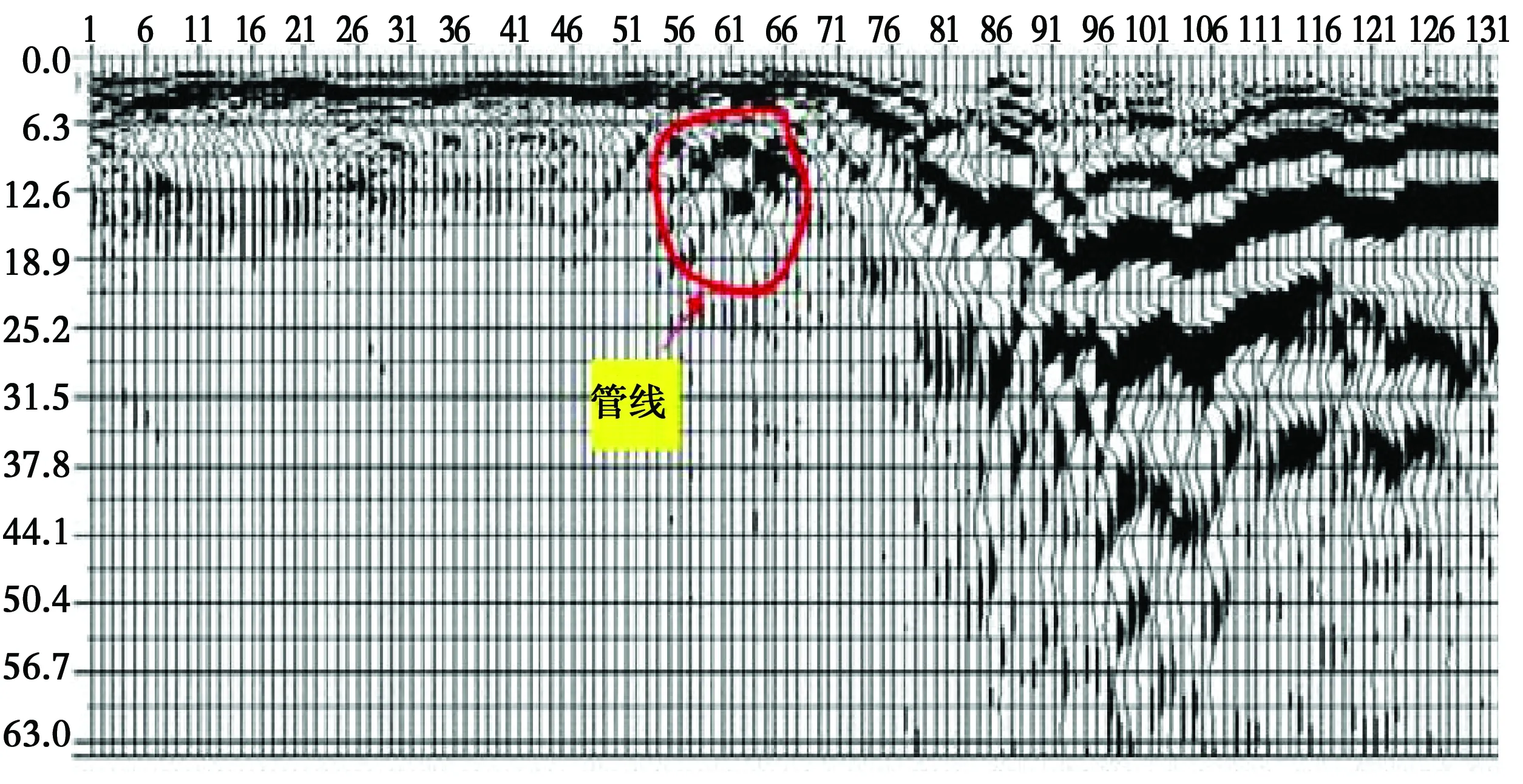
图12 瑞利波信号
从图14可以找到地下管道。该测线中1~56道为无异常体的地层结构反应;56~66道范围内在9 ms时出现了明显弧形反射信号带,信号带顶端在第60道。提取第60道的入射瑞利波和反射瑞利波的时间,代入公式得到管道的水平位置。同时,对时域图进行FFT变换得到频谱,估算管道埋深。经查阅地下管道施工图,对比分析结果,由于地下管道周边为回填土,对信号产生一定的影响,误差相对较大,但验证了该方法的正确性。
5 结论
对均匀半无限空间介质中的瑞利波的产生和波动特征进行了理论分析,运用有限元软件ABAQUS对含空洞模型进行数值模拟,得到如下结论:
1)瑞利波沿着介质表面传播过程中,遇到空洞边界,一部分波发生反射形成反射瑞利波,一部分波在边界处积聚并最终消散,一部分瑞利波在边界处发生模式转换形成衍射横波和衍射纵波,另一部分波则直接透射过去,形成透射瑞利波。
2)采用入射瑞利波和反射瑞利波的时间差能够比较准确地计算空洞具体位置,相对误差较小。
3)将瑞利波时域经FFT变换成频谱,根据频谱及瑞利波的传播规律提出了采用临界干扰频率法定量分析空洞的埋深。结果表明,其计算误差较小,该方法具有比较高的准确性。
4)提出了能量衰减率法,定量分析了空洞竖向尺寸,将得到的数据进行拟合,其计算结果误差较小,有较高的精度。

