穿越公路输气管道力学性状影响因素研究

兰国冠,赵向前,孙安勇

(1.三明学院建筑工程学院,福建三明 365004;2.中节能建设工程设计院有限公司,四川成都 610052; 3.成都博锐建筑工程咨询有限公司,四川成都 610001)

0 引 言

通常,车辆荷载作用下埋地输气管道的动力响应涉及多个学科,如道路工程、管道工程、车辆工程、岩土工程以及弹塑性力学、土力学、结构力学、随机振动理论等,是一个跨学科的交叉研究课题,用纯理论方法研究难度很大,而试验研究需要花费大量的人力、财力,且解析计算不能很好地解决复杂问题[1-5],数值模拟技术的出现恰好弥补了上述不足,有限元、边界元等数值方法逐渐流行,并成为工程计算领域中的最重要手段之一[6-10].本研究利用理论分析结合ANSYS模拟软件对穿越公路输气管道在车辆荷载作用下的力学性状进行数值模拟与分析.

1 车辆移动方向与管道垂直时的管土受力模型

车辆移动方向与管道垂直时的管土受力模型描述的是当移动荷载方向与管道垂直交叉时的受力情形.由于地基土体是一个无限空间体,在计算中本研究截取一定的范围,确定地基的三维固体有限元计算模型尺寸为,长×宽×高=10 m×5 m×5 m,软土地基的密度为1 790 Kg/m3,弹性模量为9 MPa,泊松比0.40.管道为三维固体模型,长度10 m,壁厚25 mm,埋深2 m,管道材质为钢材,密度为7 850 Kg/ m3,弹性模量为210 GPa,泊松比0.30.管道边界条件为两端设为固支.荷载大小为四分之一车重,为点荷载作用在车轮轨迹上,这里把车轮轨迹视为两条直线.

1.1 车辆模拟参数

本研究中,车辆具体模拟参数如表1所示.

表1 车辆模拟参数

1.2 土体材料参数

土体模型选用与实际土体弹塑性状态较接近的Drucker-Prager模型.该模型服从广义的Von-Mises屈服准则,其表达式[8]为:

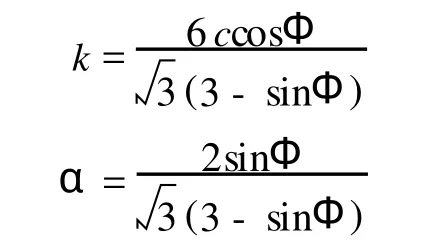
土体具体参数如表2所示.

表2 土体具体参数表

1.3 管道材料参数

本研究采用的管道为X70级管材,利用双线形硬化弹塑模型,该模型遵从Von-Mises屈服准则,其表达式[8]为,

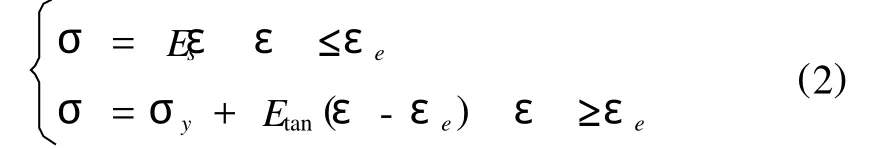
式中,σ为应力;σy为屈服应力;Es、Etan为弹性模量和切线模量;ε、εe为应变和弹性极限应变.

埋地输气管道具体参数如表3所示.

表3 埋地输气管道参数

1.4 选取单元类型及网格划分

本研究采用Solid 45及Solid 65单元来模拟土体和埋地管道.Solid 45单元由8个节点结合而成,每个节点有xyz 3个方向自由度,该单元具有塑性、蠕变、膨胀、应力强化、大变形、大应变等特征.Solid 65单元为8节点6面体单元,是和普通的8节点空间实体单元Solid 45相同的实体单元模型,但加入了Willam-Warnke 5参数破坏准则.

对建立的几何模型,需要对其划分网格生成包含节点和单元的有限元模型.有限元网格的划分过程包括3个步骤[9-10]:①定义单元属性,包括指定单元类型、分配实常数、分配材料属性等;②设置网格控制(可选择的);③生成网格.

选用有限元计算时,单元网格划分越密,计算误差越小,越接近于真实值,不过网格划分越密计算时间就越长,计算量越大.地基及管道网格划分如图1、2所示.

图1 管土模型及土体模型单元网格划分图

2 不同因素对管道应力的影响分析

2.1 车速对管道应力的影响

2.1.1 把管道中点作为研究对象,研究车速对管道应力的影响.

为了分析车辆速度对管道中点应力的影响,假设路面近似平整,在保证其他因素不变的情况下分别选取20 km/h、30 km/h、40 km/h、50 km/h、60 km/h 5个不同的车速进行模拟.取得不同车速下管道中点的应力峰值,即得管道中点Mises应力随车速变化趋势图如图3所示.

图2 横穿公路管道模型边界及单元网格划分图

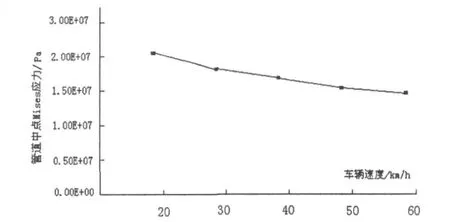
图3 管道中点Mises应力峰值随车速变化趋势图

由图3可以看出:在路面近似平整的情况下,随着车速的增大,管道受到的应力呈减小趋势,不过当车速超过45 km/h后,管道中点Mises应力变化不大,其原因是地基中的应力传递需要依靠相邻的颗粒来完成,车辆速度大,应力出现的时间就短,从而来不及向土体周边传递,应力响应特征就不那么显著.

2.1.2 把管道中点作为研究对象,研究车速对管道变形的影响.

与研究应力随车速变化一样,在保证其他因素不变的情况下分别选取20 km/h、30 km/h、40km/h、50 km/h、60 km/h 5个不同的车速进行模拟.取得不同车速下管道中点的变形峰值,即得管道中点变形随车速变化趋势图如图4所示.

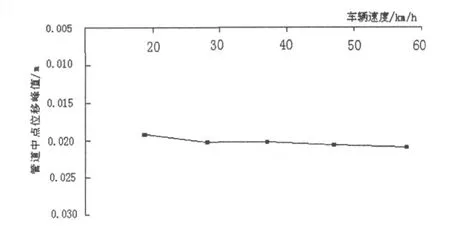
图4 管道中点位移峰值随车速变化趋势图

由图4可以看出,不同车速下,管道中点的位移响应相差不大,基本呈一条水平直线,此表明,车辆速度变化对管道变形的影响不是很大.

2.2 车辆载重的影响

为了研究车辆载重对管道应力及变形的影响,假定其他参数不变,选用一组不同载重的车辆模型,由于本研究假设车辆加载为点荷载,车辆以4个车轮计算,因此把四分之一车载重作为点荷载值.分别选用8 t、9 t、10 t、13 t、16 t 5种不同载重的车辆进行模拟,折算成四分之一点荷载分别为,F1=20 000 N、F2=22 500 N、F3=25 000 N、F4=32 500 N、F5= 40 000 N.对此,管道中点应力与位移随车载重变化趋势图如图5、6所示.

图5 管道中点Mises应力峰值随车辆载重变化趋势图

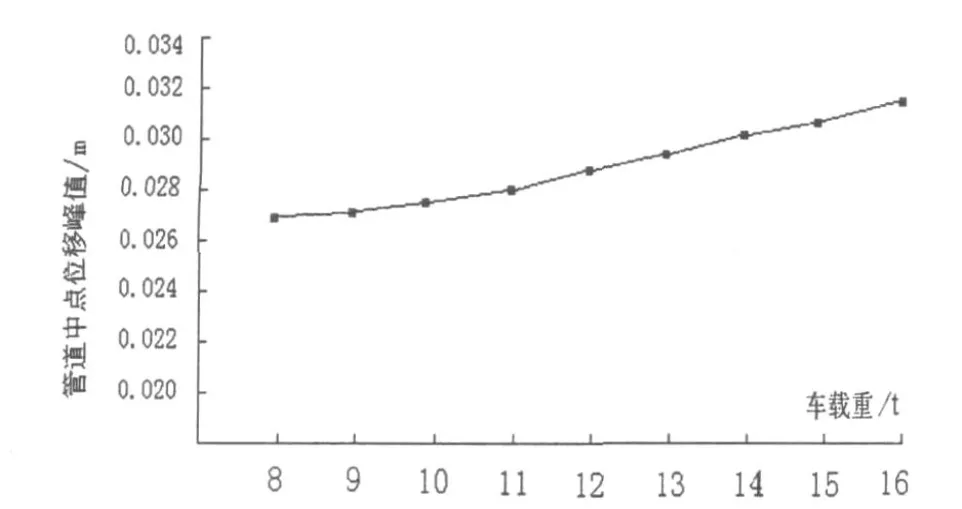
图6 管道中点位移峰值随车辆载重变化趋势图

由图5可以看出,管道中点Mises应力随车辆载重的增大而大致线性增大.由图6可以看出,当车辆载重从8 t逐渐增加到16 t的过程中,管道中点位移峰值变化幅度不大,仅变化0.003 m左右.同时,研究中还发现,随着车辆载重的增加,位移的波动减小,其原因是管道所受压力增加时,其所受的约束也相应增加,从而使位移的波动减小.

2.3 管道直径的影响

在研究管径对管道位移的影响时,保持车速及其他参数不变,分别选用3种不同管径(D=0.9 m, D=1.1 m,D=1.3 m)的管道进行模拟,最后取各管径对应的管道中点位移响应量峰值,即得位移响应峰值随管径变化趋势绘成图表如图7所示.

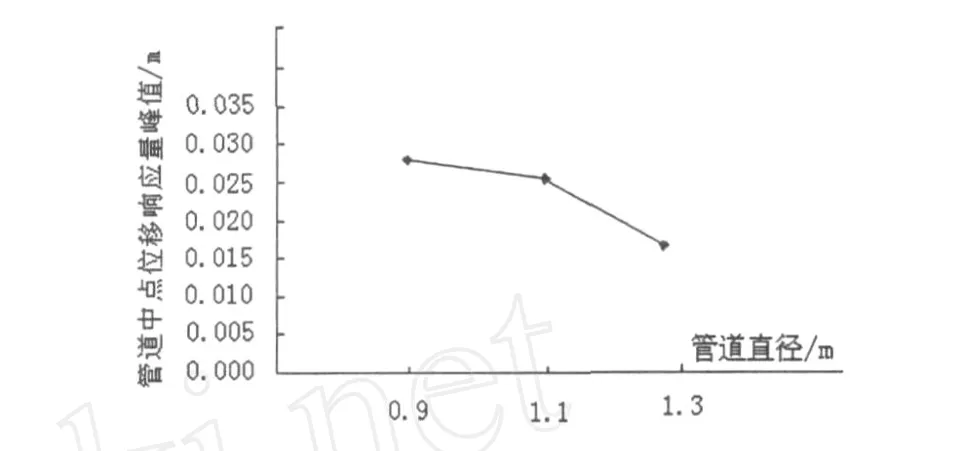
图7 管道中点位移响应峰值随管径变化图

由图7可以看出,随着管径的增大管道位移响应量减小,不过从0.9 m变化至1.1 m时,管道位移值变化量比从1.1 m变化至1.3 m时小得多.

2.4 管道埋深的影响

管道中点应力峰值随深度变化趋势如图8所示.

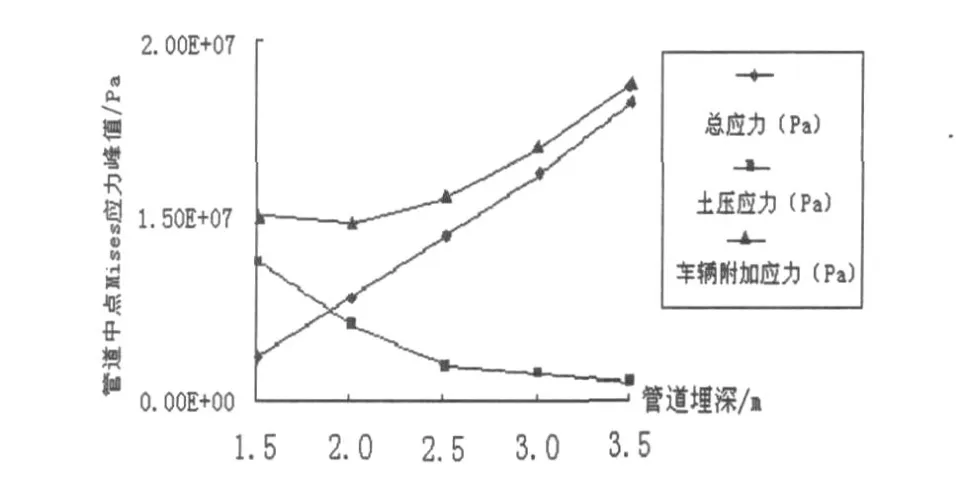
图8 管道中点应力峰值随深度变化趋势图

由图8可以看出,土体压力随着埋深的增加而线性增大,而车辆产生的附加应力则随着埋深的增加而快速减小,其原因在于土体的阻尼特性及扩散作用使车辆产生的附加应力在深处渐渐消散,所以管道所受总应力就呈现先减小后增大的趋势.根据总应力最小的原则,我们可以确定一个最佳管道埋深,如图8所示,最佳埋深为2 m左右.当然,在实际工程中确定最佳埋深时,还要考虑不同规格管道对其埋深的专业要求及经济指标等因素,综合评定.而且刚性管道与柔性管道的埋深要求是不同的,实际工程应用时应注意二者的区别.

2.5 地基弹性模量的影响

在保持其他参数不变的情况下,分别选用地基弹性模量为,E=8 Mpa、E=10 Mpa、E=12 Mpa、E= 14 Mpa、E=16 Mpa,进行模拟,管道中点Mises应力峰值与位移峰值随地基弹性模量变化如图9、10所示.

由图9可知,应力峰值随着地基弹性模量的增大而呈减小趋势,大致成反比例关系.

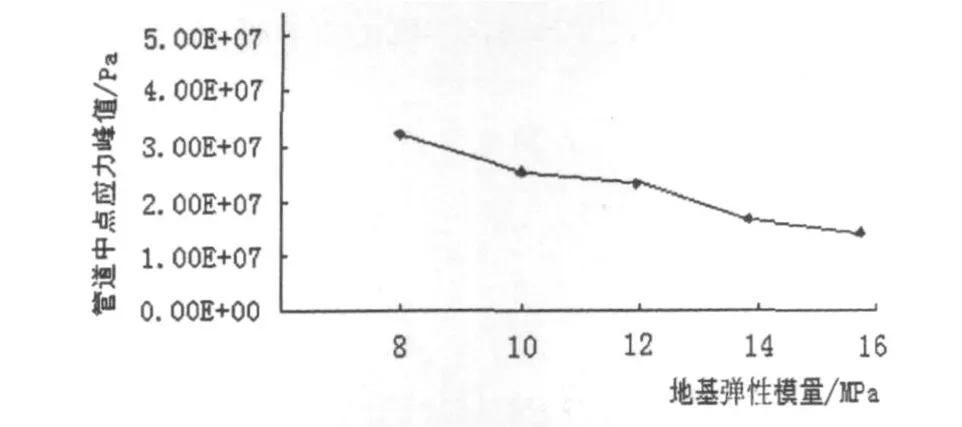
图9 管道中点Mises应力峰值随地基模量变化趋势图

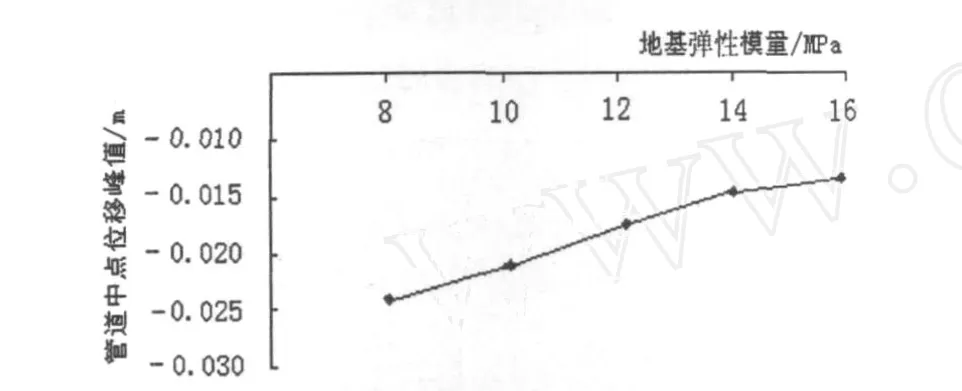
图10 管道中点位移峰值随地基变形模量变化趋势

由图10可知,位移随地基模量变化趋势与应力图类似,都是大致成反比例的关系,地基弹性模量越大,管道位移量越小.

2.6 地基泊松比的影响

管道中点Mises应力峰值及位移随地基泊松比变化趋势如图11、12所示.

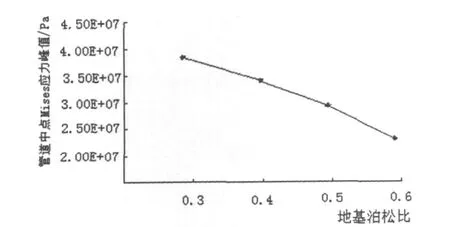
图11 管道中点Mises应力峰值随地基泊松比变化趋势

由图11可知,随着泊松比的增大,管道应力峰值减小,且影响幅度较大,说明泊松比是影响车辆荷载作用下管道应力值的重要因素.

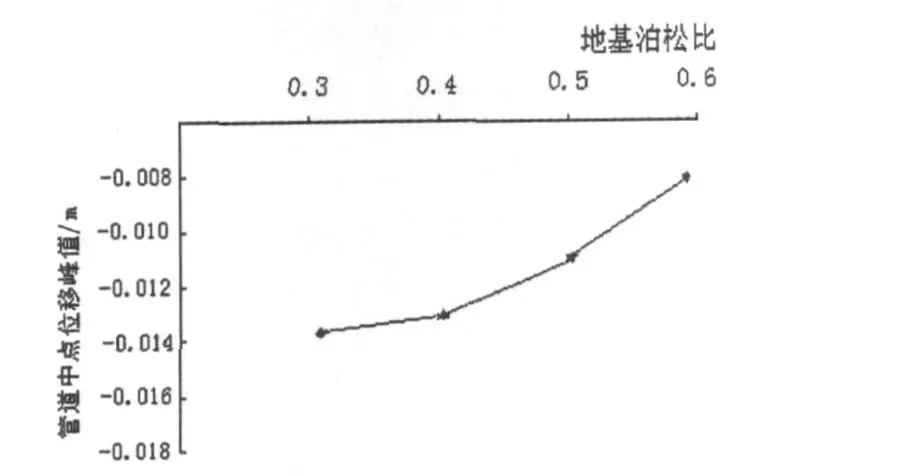
图12 管道中点位移峰值随地基泊松比变化趋势

由图12看出,管道中点位移峰值随泊松比的变化与应力变化类似,随着地基泊松比的增大,位移峰值逐渐减小.管道中点位移值与地基泊松比大致成反比例关系.

3 结 语

本文通过软件数值模拟,得到了横穿道路管道受车辆荷载作用时管道中点应力及竖向位移随时间变化的时程图等,并对影响管道力学性状的各种因素进行了分析和总结,各因素的影响概述如下:

(1)随着车速的增大,管道受到的应力呈减小趋势,不过当车速超过45 km/h后,管道中点Mises应力变化不大,其原因是地基中的应力传递需要依靠相邻的颗粒来完成,车速大,应力出现的时间就短,从而来不及往土体周边传递,应力响应特征就不那么显著.

(2)管道中点Mises应力随车辆载重的增大而大致线性增大,随着车辆质量的增加,位移的波动减小.

(3)随着管径的增大管道位移响应量减小,且在相同管径级差时,较大管径之间的位移响应量更小.

(4)土体压力随着埋深的增加而线性增大,而车辆荷载产生的附加应力则随着埋深的增加而快速减小,所以管道所受总应力就呈现先减小后增大的趋势,根据总应力最小的原则,可以确定一个最佳管道埋深,在本例中所示,最佳埋深为2 m左右.

(5)管道应力峰值随着地基模量的增大而呈减小趋势,大致成反比例关系.

(6)管道中点位移值与地基泊松比大致成反比例关系.

[1]候忠良.地下管线抗震[M].北京:学术书刊出版社,1990.

[2]邓学钧,孙璐.车辆—地面结构系统动力学[M].北京:人民交通出版社,2000.

[3]吴为义.垂直荷载作用下软粘土地基中管道的纵向力学性状研究[D].杭州:浙江大学,2000.

[4]李询.交通荷载作用下埋地管道的力学性状分析[D].浙江大学,2004.

[5]周华飞,蒋建群,毛根海.路面不平整引起的车辆动荷载分析[J].中国市政工程,2002,99(3):10-13.

[6]徐建平,尚刚,梁乃兴.路面不平整引起的汽车动荷载计算分析[J].重庆交通学院学报,2001,20(1):26-28.

[7]吴小刚.交通荷载作用下软土地基中管道的受力分析模型研究[D].杭州:浙江大学,2004.

[8]赵师平,曾祥国.第三方荷载作用下埋地输气管道动力响应的数值模拟[J].四川建筑科学研究,2009,35(1):134-139.

[9]刘全林,杨敏.地埋管与土相互作用分析模型及其参数确定[J].岩土力学,2004,25(5):728-731.

[10]张土乔,陈观胜.垂直荷载作用下管道的受力模式研究[R].杭州:浙江大学土木系、杭州市市政工程总公司, 1999.

[11]张方锐.ANSYS 8.0应用基础与实例教程[M].北京:电子工业出版社,2006.