基于支持向量机回归的机械零件可靠性分析

程 跃，郑 严

(1.成都大学工业制造学院，四川成都 610106;2.西南交通大学机械工程研究所，四川成都 610031)

0 引言

机械零件作为机构的重要组成部分，其可靠性程度对于整个机构的安全运行具有非常重要的意义.建立极限状态方程(Limit State Function，LSF)是进行机械零件可靠性分析的前提条件，但在通常情况下，对于复杂的机构，机械零件的极限状态方程与基本随机变量之间不存在显式关系.目前，解决这类问题常见的方法是利用响应面法(Response Surface Method，RSM)［1］和Kriging法［2］，其思路是将隐式极限状态方程进行显式化重构处理，然后再采用显式极限状态方程的可靠性分析方法进行机械零件的可靠度计算.虽然这2种方法在实际结构的可靠性分析中取得了一定的成果，但仍存在一些问题，比如，当结构极限状态方程非线性程度较高时，RSM的二次多项式模型很难真实地刻画极限状态方程，若使用高阶多项式模型，则待定系数较多，需要更多的样本点，从而导致计算效率下降［3］.因此，在RSM的基础上有学者提出了非参数化的RS模型—Kriging方法，该方法在一定程度上解决了对高度非线性方程的近似，但是其建模过程也更为复杂［3］.

支持向量机(Support Vector Machine，SVM)［4，5］是Vapnik等根据统计学习理论中结构风险最小化原则提出的借助最优化方法的机器学习系统.SVM具有优良的小样本学习和预测能力，具有良好的泛化性能，能克服传统的“维数灾难”难题.本研究通过对国内外相关文献的分析发现，机械零件可靠性分析目前常用的方法有一次二阶矩法、随机有限元法和蒙特卡罗法等，但很少有将SVM应用于机械零件可靠性分析中［6－8］.基于此，本研究利用支持向量机回归(Support Vector Regression，SVR)来拟合隐式极限状态方程，结合改进的一次二阶矩法，给出了基于SVR的机械零件可靠性分析方法，并用2个算例证了该方法的可行性、正确性和计算精度.

1 SVR描述

设l个给定的数据样本对，{(x1，y1，x2，y2，…，xl，yl)}，其中，xi=［x1i，x2i，…，xni］为n维输入向量，yi为对应的输出向量，i=1，2，…，l.SVR就是在高维特征空间中寻找一个线性函数，f(x)=wФ(x)+ b，其中，Ф(x)为非线性映射函数，以便用f(x)来预测任一输入x所对应的输出y值［9－11］.通常，SVR需定义ε线性不敏感损失函数，L(f(x)，y，ε)，如图1所示.

图1 ε线性不敏感损失函数

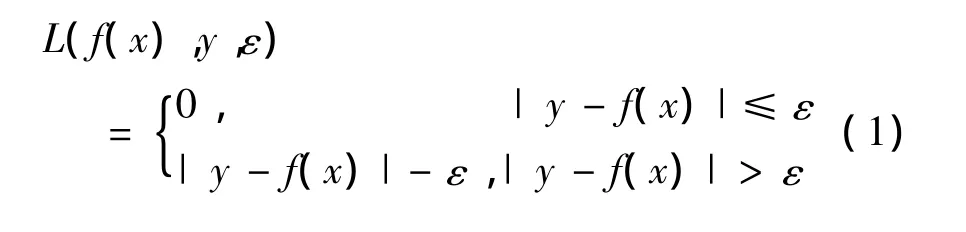
式中，y为真实输出值，f(x)为预测输出值，ε为线性不敏感损失函数，表示当f(x)与y之间的差值在［－ε，ε］范围内时，该损失等于0，是可以忽略的.

同时，引入松弛变量ζi和ζ*i，确定函数f(x)= wФ(x)+b，中的w和b值可转换为求解如下优化问题［5，9－11］:

式中，C为惩罚因子.引入Lagrange函数可得到优化问题(2)的对偶形式［5，9－11］:

式中，αi和 α*i为Lagrange乘子向量，K(xi，xj)= Ф(xi)Ф(xj)为核函数.

求解式(3)得最优解，

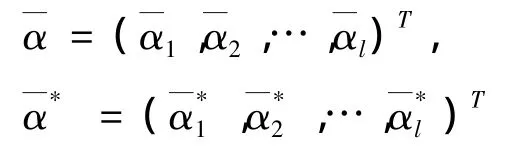
则，

式中，N为支持向量个数，SV为支持向量集.

则，回归预测函数f(x)为，

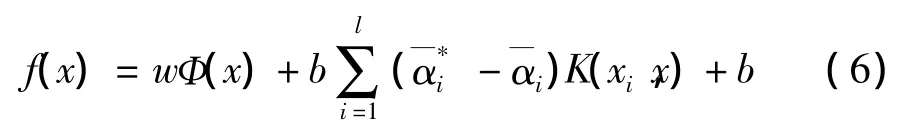
2 基于SVR的机械零件可靠性分析流程

基于SVR的机械零件可靠性分析流程如图2所示.

在对机械零件进行可靠性分析时，一般对于较为复杂的机构而言，零件的极限状态方程，Z= g(X)，与影响其可靠性的n个随机变量，X1，X2，…，Xn，之间不存在显式关系，导致机械零件的可靠性分析需付出较大的计算代价.对此，我们利用SVR优良的小样本学习和预测能力对隐式极限状态方程进行显式化重构处理，结合改进的一次二阶矩法，给出一种基于SVR的机械零件可靠性分析方法，其具体步骤为:

图2 基于SVR的机械零件可靠性分析流程示意图

(1)在进行SVR训练之前，首先采用中心复合抽样方法获得一定数量的数据样本点x，由Ansys分析计算每个样本点xi对应的输出yi，从而获得一定数量的样本对.一般情况下，机械零件可靠性分析中的随机变量为零件所承受的外载荷、零件的几何形状和尺寸、零件材料的物理特性等，这些随机变量各自的取值范围差别较大，在SVR训练中容易出现不稳定性和泛化性差的现象.所以，在SVR训练程序之前应加入归一化数据程序，训练测试完毕之后再反归一化输出数据.

(2)对样本对进行数据归一化处理后，本研究参考林智仁教授的LIBSVM分析软件进行SVR训练.通过反复调试和测试SVR模型精度，选取合适的核函数和SVR参数，从而获得高精度的显式化极限状态方程.通过假定初始设计点并对各随机参数进行标准化变换，利用改进一次二阶矩法求解机械零件可靠性指标β值.

3 算 例

下面通过1个假定的隐式极限状态函数算例和1个实际工程算例来验证本文所提方法在机械零件可靠分析中的可行性、正确性和计算精度.

3.1 数值算例

设极限状态函数为，

式中，x1，x2，x3为独立标准正态分布的随机变量.各随机变量的均值和标准差为，μx1=3，σx1=0.6，μx2=5，σx2=0.75，μx3=8，σx3=0.8.

按照前述抽样策略，抽取110个样本，并将其全部作为训练样本，其中随机抽取30个作为测试样本.将所有样本对进行数据归一化处理后，反复调试，选取多项式核函数，K(xi，xj)=［G×(xi·xj)+ r］d，ε-SVM回归，G=3，r=1，d=3，损失函数，ε=0.0001，惩罚参数，C=1 000.将训练样本对进行SVR训练，然后用测试样本对进行检验，最大绝对误差为0.0185，最小绝对误差为0.0001，其相对误差曲线如图3所示.

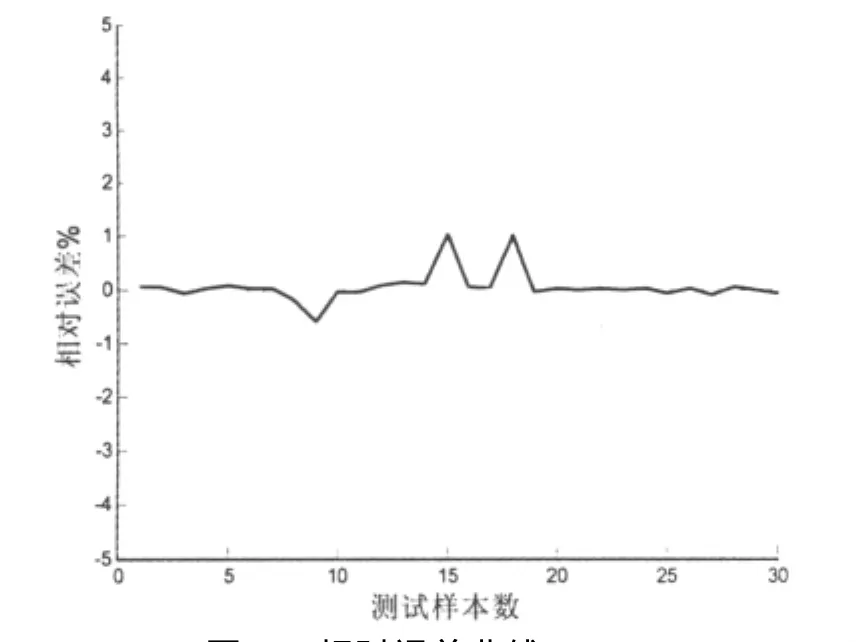
图3 相对误差曲线

图3所示相对误差曲线表明，SVR预测精度较好，证明了用SVR模型替代真实极限状态方程进行可靠性分析是可行的.

同时，利用本文方法和MC法计算其失效概率和可靠度指标结果列于表1.

表1 数值算例的计算结果

从表1数据可以看出，本文方法的计算结果非常接近MC法的结果，验证了本文方法的正确性和计算精度.

3.2 工程算例

计算某剪切机上联接销可靠性，此联接销共有2个，用来联接油缸活塞杆(剪切缸杆)与刀架小车.在组件剪切过程中，推力由活塞杆的端头承受，当剪切完成后，活塞杆收缩，通过联接销带动刀架小车运动，联接销承受剪切缸杆的拉力.联接销承受载荷和约束情况如图4所示.

图4 联接销承受载荷与约束示意图

根据此联接销的实际工作情况，选择外载荷、弹性模量、泊松比、屈服极限以及联接销与其他物体之间的摩擦系数作为输入变量.各变量的统计参数如表2所示.

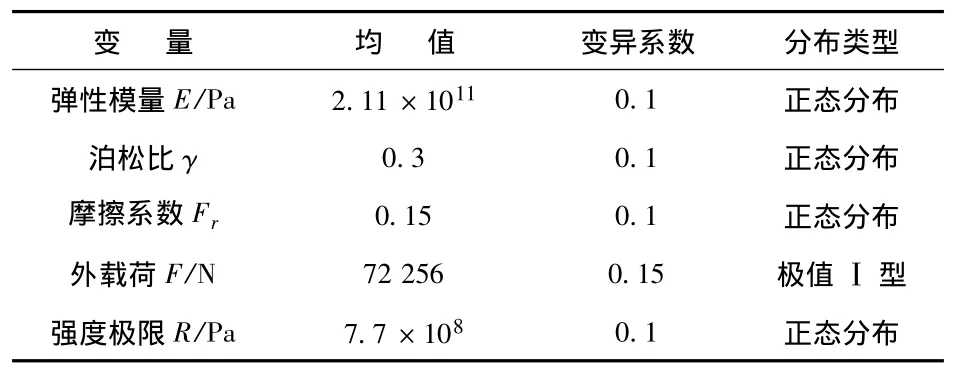
表2 联接销各变量统计参数

根据“应力—强度干涉”模型可得出联接销的极限状态方程为，

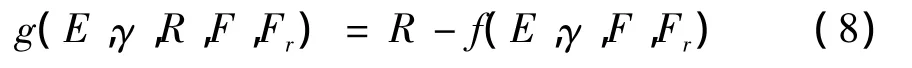
根据前述抽样策略，抽取200个样本点，利用有限元分析计算得到每一个样本点对应的f(E，γ，F，Fr)数值解，从而得到200个样本对.将获得的200个样本对全部作为训练样本对，随机抽取50个作为测试样本对.将输入样本对进行数据归一化处理后，经过参数调试，选取多项式核函数，ε-SVM回归，G =26，r=1，d=6，损失函数，ε=0.0005，惩罚参数，C=109.将本文方法与MC法和RSM进行比较，计算结果见表3.

表3 工程算例的计算结果

从表3数据可以看出，本文方法与RSM的计算效率相当，均比MC法效率高.并且本文方法的计算结果最为接近MC法的结果，相对误差较小，计算精度高.

4 结 论

以SVR为极限状态方程的重构工具，拟合实际机械零件的隐式极限状态方程，结合改进的一次二阶矩法，提出了一种基于SVR的机械零件可靠性分析方法.该方法充分利用了SVR优良的小样本学习能力，全局寻优和良好的泛化性能，提高了可靠性计算的效率和精度.同时，本文通过数值算例证明了用SVR模型替代真实极限状态方程进行可靠性分析是可行的，并利用该方法对某剪切机上的联接销进行可靠性分析，方法的计算结果最为接近MC法的结果，相对误差较小，计算精度高.

［1］Hurtado J E.An Examination of Methods for Approximating Implicit Limit State Functions from the Viewpoint of Statistical Learning Theory［J］.Structural Safety，2004，26(3):271－293.

［2］Kaymaz I.Application of Kriging Method to Structural Reliability Problems［J］.Structural Safety，2005，27(2):133－151.

［3］张建国，苏多，刘英卫.机械产品可靠性分析与优化［M］.北京:电子工业出版社，2008.

［4］李洪双，吕震宙，岳珠峰.结构可靠性分析的支持向量机方法［J］.应用数学与力学，2006，27(10):1136－1143.

［5］白鹏，张喜斌，张斌，等.支持向量机理论及工程应用实例［M］.西安:西安电子科技大学出版社，2008.

［6］Rocco C M，Moreno J A.Fast Monte Carlo Reliability Evaluation Using Support Vector Machine［J］.Reliability Engineering and System Safety，2002，76(3):237－243.

［7］Hurtado J E，Alvarez D A.Classification Approach for Reliability Analysis with Stochastic Finite-element Modeling［J］.Journal of Structural Engineering，2003，129(8):1141－1149.

［8］Zhao Hongbo.Slope Reliability Analysis Using a Support Vector Machine［J］.Computers and Geotechnics，2008，35(3): 459－467.

［9］史峰，王辉，郁磊，等.MATLAB智能算法30个案例分析［M］.北京:北京航空航天大学出版社，2011.

［10］Guo Zhiwei，Bai Guangchen.Application of Least Squares Support Vector Machine for Regression to Reliability Analysis［J］.Chinese Journal of Aeronautics，2009，22(2):160－166.

［11］Cristianini N，Shawe-Tayler J.An Introduction to Support Vector Machines and Other Kernel-based Learning Methods［M］.Cambridge:Cambridge University Press，2000.